当前位置：文档之家 › 材料力学习题册答案-第13章-能量法

材料力学习题册答案-第13章-能量法

  • 格式：doc
  • 大小：819.04 KB
  • 文档页数：8

下载文档原格式

  / 8

合集下载

材料力学第十三章 能量法

材料力学第十三章 能量法

1 vε = = τγ 2G 2
τ2
三、扭转
由实验知，线弹性范围内，扭转角与扭转力偶成线性关系： 由实验知，线弹性范围内，扭转角与扭转力偶成线性关系：
M e l M e 2l 1 1 Vε = W = M e ⋅ ∆φ = M e = 2 2 G I p 2G I p
T 2 ( x) Vε = ∫ dx 2G I p ( x) l
截面的挠度。 例：求图示简支梁C截面的挠度。 求图示简支梁 截面的挠度
F
θ B2
wC1
解：由功的互等定理 F ⋅ wC1 = M ⋅ θ B 2
得：F ⋅ wC1
Fl =M⋅ 16 E I Ml = 16 E I
2
2
由此得：wC1
例：求图示悬臂梁中点C处的铅垂位移∆ C 。 求图示悬臂梁中点 处的铅垂位移
故：
M ( x) M ( x) ∆=∫ dx EI l
M ( x) M ( x) 莫尔定理 ∆=∫ dx 莫尔积分） （莫尔积分） EI l
对于组合变形： FN ( x) FN ( x) T ( x) T ( x) M ( x) M ( x) ∆=∫ dx + ∫ dx + ∫ dx EA GI p EI l l l
积分得： 积分得：
FN (x)dx M (x)dx T (x)dx Vε = ∫ +∫ +∫ 2EA 2EI 2GIP L L L
2
2
2
例：试求图示悬臂梁的应变能，并利用功 试求图示悬臂梁的应变能，并利用功 求自由端B的挠度 能原理求自由端 的挠度。 能原理求自由端 的挠度。
F
解：
B
A
l
x
M ( x) = − F ⋅ x

材料力学课后习题答案13章

材料力学课后习题答案13章

= 7.44 × 10− 2 m = 74.4mm
而
2 × 0.050 Fd = (300 N ) 1 1 + + 2.22 × 10 − 2
= 1.004 × 10 3 N
M max = 1.004 ×10 3 N (1.00m ) = 1.004 ×10 3 N ⋅ m
设压杆微弯平衡时的挠曲轴方程为
πx w = f sin l
式中，f 为压杆中点的挠度即最大挠度。
题 13-8 图 解：由题设可知，
w = f sin
πx , l
6
w′ =
πf πx cos l l
据此可得
λ (x ) =
q cr 所作之功为
1 x 2 * 1 ( w′) dx = 2 0 2
∫
∫
x 0
(也可通过左侧题号书签直接查找题目与解)
13-2
比为 8:3。
图示圆截面简支梁，直径为 d，承受均布载荷 q 作用，弹性模量 E 与切变模量 G 之
（1）若同时考虑弯矩与剪力的作用，试计算梁的最大挠度与最大转角； （2）当 l/d =10 与 l/d =5 时，试计算剪切变形在总变形（最大挠度与最大转角）中所占百分比。
（2）被冲击面（弹簧顶面）的静位移为
∆st =
最大冲击载荷为
Pl P 500 + = 1.516 × 10 − 5 m + m = 2.52 × 10 − 3 m 3 EI k 200 × 10
2h + + Fd = P 1 1 ∆ st
于是，杆内横截面上最大的正应力为
Fl 3 ∆= 48EI
得刚度系数
0.030 4 48 × 200 × 10 × F 48 EI 12 N = 6.48 × 10 5 N k= = 3 = 3 ∆ m m l 1.00

材料力学第十三章 能 量 法

材料力学第十三章 能 量 法

Vε Vε (D1 , D 2 ,, D i ,, D n )
假设位移 Di 有一微小增量 dDi 其它位移均保持不变 梁的应变能也有一增量 dVe
外力功的增量
d W Fi d D i
Ve d Ve d Di D i
d Ve d W
Ve Fi D i
卡氏第一定理
卡氏第一定理
Vε
l
0
F ( x) T ( x) dx dx 0 2GI 2 EA p
l
2 N
2
F ( x) M ( x) d x s dx 0 2 EI 0 2GA
l l
2
2 S
应变能恒为正 ，是内力或外力的二次函数。
非线性函数
一般情况：非线性弹性体
s s1 s e
外力作功：
de e 1
DAB 方向水平向外
§3-4 用能量法解超静定系统
解超静定问题要综合考虑三方面 几何方面 —— 建立变形几何相容条件 物理方面 —— 建立补充方程 静力学方面 —— 建立平衡方程
等直杆，发生基本变形，材料为线性弹性体 非等直杆或杆系结构，受较复杂荷载作用， 材料为非线性弹性体 易 难
能量法
例1：求图示超静定梁支座处的约束力。
③ 先加M，后加F
A
M AM
F
B
AF DCF
AM
Ml 3EI
D CF
Fl 48 EI
3
AF
Fl 16 EI
2
1 1 应变能： V M ε AM ( FD CF M AF ) 2 2 2 3 2 2 1 F l M l MFl ( ) EI 96 6 16
Ve Fi D i

材料力学-第十三章能量方法

材料力学-第十三章能量方法

fc
U P
M (x) M (x) dx
l EI P
1
EI
l 2 0
[(
P 2
Me l
) x1
M
e
]
x1 2
dx1
1 EI
l 2
(
P
02
Me l
) x2
x2 2
dx2
M el 2 Pl3 16EI 48EI
(
)
31
• 例13-6 求刚架B的水平位移和C点的转角。
解:
AB段： M (x1) (Pa Pf x1)
P
2
29
A截面的转角:
A
U M e
M (x) M (x) dx l EI M e
1
EI
l
2 [(
0
P 2
Me l
) x1
M e ](1
x1 l
)dx1
1
EI
l 2 0
(P 2
Me l
) x2
x2 l
dx2
M el 3EI
Pl 2 16EI
(
)
30
Me
p
A
C
X1
L/2 L/2
B
X2
C截面的挠度为:
A ②将内力对MA求偏导后，令M A=0
L xO
③求变形（ 注意：M A=0）
M (x)
1
M A M 0
A
A
L
M (x) M (x) dx EI M A
L Px dx 0 EI
PL2
2 EI
A
PL2 ( 2 EI
)
“负号”说明 A与所加广义力MA反向。

昆明理工大学材料力学A80学时练习册1-13章答案

昆明理工大学材料力学A80学时练习册1-13章答案

第一章 绪论一、是非判断题1.1 ( × )；1.2 ( × )；1.3 ( × )；1.4 ( ∨ )；1.5 ( ∨ )；1.6 ( ∨ ) 1.7 ( ∨ )；1.8 ( × )；1.9 ( × )；1.10 ( ∨ )；1.11 ( ∨ )1.12 ( ∨ )；1.13 ( × )；1.14 ( ∨ )；1.15 ( ∨ ) ；1.16 ( × )二、填空题1.1 杆件 变形 ， 应力，应变 。

1.2 外力的合力作用线通过杆轴线 ， 沿杆轴线伸长或缩短 。

1.3 受一对等值，反向，作沿剪切面发生相对错动 ， 沿剪切面发生相对错动 。

1.4 外力偶作用面垂直杆轴线 。

任意二横截面发生绕杆轴线的相对转动 。

1.5 外力作用线垂直杆轴线，外力偶作用面通过杆轴线 ， 梁轴线由直线变为曲线 。

1.6 包含两种或两种以上基本变形的组合 。

1.7 强度 ， 刚度 ， 稳定性 。

1.8 强度 ， 刚度 ， 稳定性 。

1.9 连续性 ， 均匀性 ， 各向同性 。

1.10 连续性假设 。

应力 、 应变 变形等 。

1.11 拉伸 ， 压缩 ， 弯曲 。

1.12 2α ； α-β ； 0 。

三、选择题1.1 1 。

1.2 C 。

1.3 C 。

四、计算题1.10=A X ∑=0X FF S =⇒∑=0Y 0=-F Y A F Y A =⇒∑=0A M 0=--FL M FL M -=⇒y x解：1. 求A 端的反力： 2. 求1-1截面的内力： ∑=0Y 0=F F S-∑=01C M 02=--/FL M 2/FL M -=⇒X A M1.2第二章 拉伸、压缩与剪切一、是非判断题2.1 ( × )；2.2 ( ×)；2.3 ( × )；2.4. ( ×)；2.5 ( × )；2.6 ( × ) 2.7 ( × )；2.9 ( × )；2.10 ( × )；2.11（ × ）；2.12（ ∨ ）二、填空题2.1 2.22.3 最大工作应力σmax 不超过许用应力[σ] ， 强度校核 ； 截面设计 ； 确定许可载荷 。

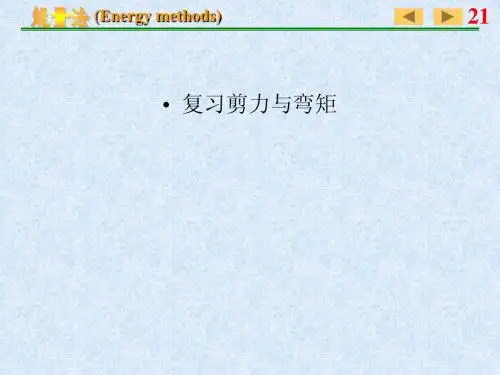
材料力学第十三章 能量法2013

材料力学第十三章 能量法2013

§13-7 计算莫尔积分的图乘法 ★重点
(Energy methods)
§13-1 概述（Introduction)
能量方法 (Energy methods )
利用功能原理 U = W 来求解可变形固体的位移、变形和内 力等的方法.
功能原理（Work-energy principle) 外力功等于变形能
2
Me ( x) U dx l 2 EI ( x )
2
(Energy （ Strain energy density for pure shearing state of stresses )
1 u ηγ 2
将 = G 代如上式得
G 2 2 u γ 2 2G
F1a
F2
M图
a B x A
F1a+F2l
特点：在刚节点处，弯矩值连续 ;
(Chapter Thirteen)
(Energy Method)
(Energy methods)
第十三章 能量法 (Energy Methods)
§13-1 概述（Introduction) §13-2 杆件变形能的计算及普遍表达式 §13-3 互等定理（Reciprocal theorems) §13-4 卡氏定理(Castigliano’s Theorem) §13-5 虚功原理（了解） §13-6 单位荷载法 莫尔定理 ★重点
2、利用功能原理计算变形 （Work-energy principle for calculating deflection)
2 FN ( x) T 2 ( x) M 2 ( x) U dx dx dx l 2 EA( x ) l 2GI ( x ) l 2 EI ( x ) p

材料力学 第十三章能量方法

材料力学 第十三章能量方法

杆件的应变能在数值上等于变形过程中外力所做的功。 在线弹性范围内，外力由零开始缓慢增加到某一值，将外 力做的功统一写成
V
W

1 2
F
式中 F——广义力；
δ——与广义力对应的位移，即为广义力作用 点且与广义力方向一致的位移。称为广义位移。
6
§13-1 杆件应变能的计算
例题13-1
求图示悬臂梁的应变能V 和自由端的挠度yA。已知梁的抗弯刚度为EI。
拉压
dV

FN2 x 2EAx
dx
V l 2FEN2Axxdx
扭转
T 2x dV 2GIP x dx
弯曲
M 2x dV 2EIx dx
T 2x
V l 2GIP xdx
M 2x
V l 2EIxdx
5
§13-1 杆件应变能的计算
10
应变能不能叠加:
简单说明
A：F1单独作用 B：F2单独作用
1 V1 2 F1l1
V 2

1 2
F2l2
F2
F1
F2
F1
E：同时加F1、 F2
C：先加F1，再加F2
常力F1在 Δl2上作功
V

1 2
F1l1

1 2
F2l2
F1l2
F1

F12l 2EA

F2 2l 2EA
15
F112 F2 21
上式表明第一组力F1在第二组力引起的位移δ12上所做的 功，等于第二组力F2在第一组力引起的位移δ21上所做的功。 这就是功的互等定理 在F1=F2的情况下，由功的互等定理可得

1 2
Fy

材料力学习题及答案

材料力学习题及答案

材料力学-学习指导及习题答案第一章绪论1-1 图示圆截面杆，两端承受一对方向相反、力偶矩矢量沿轴线且大小均为M的力偶作用。

试问在杆件的任一横截面m-m上存在何种内力分量，并确定其大小。

解：从横截面m-m将杆切开，横截面上存在沿轴线的内力偶矩分量M x，即扭矩，其大小等于M。

1-2 如图所示，在杆件的斜截面m-m上，任一点A处的应力p=120 MPa，其方位角θ=20°，试求该点处的正应力σ与切应力τ。

解：应力p与斜截面m-m的法线的夹角α=10°，故σ＝p cosα=120×cos10°=118.2MPaτ＝p sinα=120×sin10°=20.8MPa1-3 图示矩形截面杆，横截面上的正应力沿截面高度线性分布，截面顶边各点处的正应力均为σmax=100 MPa，底边各点处的正应力均为零。

试问杆件横截面上存在何种内力分量，并确定其大小。

图中之C点为截面形心。

解：将横截面上的正应力向截面形心C简化，得一合力和一合力偶，其力即为轴力F N=100×106×0.04×0.1/2=200×103 N =200 kN其力偶即为弯矩M z=200×(50-33.33)×10-3 =3.33 kN·m1-4 板件的变形如图中虚线所示。

试求棱边AB与AD的平均正应变及A点处直角BAD的切应变。

解：第二章轴向拉压应力2-1试计算图示各杆的轴力，并指出其最大值。

解：(a) F N AB=F, F N BC=0, F N，max=F(b) F N AB=F, F N BC=－F, F N，max=F(c) F N AB=－2 kN, F N2BC=1 kN, F N CD=3 kN, F N，max=3 kN(d) F N AB=1 kN, F N BC=－1 kN, F N，max=1 kN2-2 图示阶梯形截面杆AC，承受轴向载荷F1=200 kN与F2=100 kN，AB段的直径d1=40 mm。

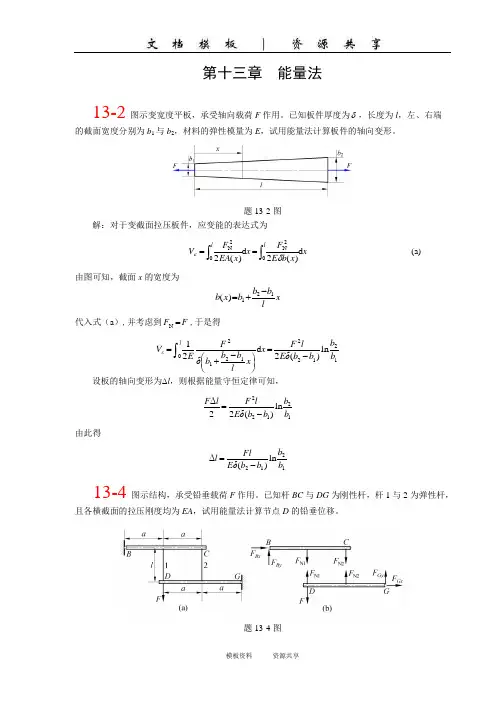
资料：ch13 能量法(3rd)

资料：ch13 能量法(3rd)

第十三章 能量法13-2 图示变宽度平板，承受轴向载荷F 作用。

已知板件厚度为δ，长度为l ，左、右端的截面宽度分别为b 1与b 2，材料的弹性模量为E ，试用能量法计算板件的轴向变形。

题13-2图解：对于变截面拉压板件，应变能的表达式为x x b E F x x EA F V lld )(2d )(202N02N⎰⎰==δε(a)由图可知，截面x 的宽度为x lb b b x b 121)(-+= 代入式（a ）,并考虑到F F =N ,于是得121221212 0 ln )(2d 21b b b b E δlF x x l b b b δF E V lε-=⎪⎭⎫ ⎝⎛-+=⎰设板的轴向变形为∆l ，则根据能量守恒定律可知， 12122ln )(22Δb b b b E δl F l F -= 由此得1212ln )(Δb b b b E δFll -=13-4图示结构，承受铅垂载荷F 作用。

已知杆BC 与DG 为刚性杆，杆1与2为弹性杆，且各横截面的拉压刚度均为EA ，试用能量法计算节点D 的铅垂位移。

题13-4图解： 1. 轴力计算未知支反力四个，未知轴力两个，即未知力共六个，而独立或有效平衡方程也为六个，故为一静定问题。

设杆1与杆2均受拉，则刚性杆BC 与DG 的受力如图b 所示。

由平衡方程 02 ,0N2N1=⋅+⋅=∑a F a F M B 022 ,0N2N1=⋅-⋅-⋅=∑a F a F a F M G得34N1F F =， 32N2FF -= 2. 铅垂位移计算 结构的应变能为EA l F EA l F EA l F EA l F V ε9103234222222222N 21N =⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛=+= 设节点D 的铅垂位移∆Dy 与载荷F 同向，因此，载荷F 所作的功为2DyF ΔW =根据能量守恒定律，于是有EAlF F ΔDy 91022= 由此得节点D 的铅垂位移为()↓=920EAFlΔDy 13-5 图a 所示圆柱形大螺距弹簧，承受轴向拉力F 作用。

材料力学第13章1-能量法-变形能计算

材料力学第13章1-能量法-变形能计算

DB EA sin 2
16
13-3 应变能的普遍表达式
❖基础知识
线弹性结构上受一个外力作用，任一点的位移与该力成正比。
线弹性结构上任意一点的广义位移与各广义力成线性齐 次关系。
比例加载时，线弹性结构上任一外力作用点沿外力方向的 位移与该点的广义力成正比。
应变能只取决于受力变形的最终状态，因此可采用便于计算 的方式计算应变能。
对于双向弯曲弯矩沿形心主轴分解dxeidxeidxei换成若杆件及杆系的变形是以弯曲变形为主的因轴力和剪力远小于弯矩对变形的影响故在计算这类杆件的变形时通常不计轴力和剪力的影响
1
本节重点—你准备好了吗？
• 1、简单变形的变形能计算； • 2、功能原理解决简单题目； • 3、互等定理的理解及应用。
第十三章 能量法
解： M( x) F x
F
Vε
M 2 (x) dx
l 2EI
A
l (Fx)2 dx F 2l3
0 2EI
6EI
W
1F 2
wB
由Vε=W 得
wB
Fl 3 3EI
B x l
11
例题2 试求图示梁的变形能,并利用功能原理求C截面
的挠度.
解：
A
Vε
M 2( x)dx l 2EI
a 0
(
工程结构形状复杂，受力复杂。利用能量法可以求结 构任一指定点的任意方向的位移，且求解过程简单。
能量法的特点
1．解题简单、适用性广； 2．不受材料和形状限制，适用于线弹性、非线性和塑性
问题；（只讨论线弹性问题） 3．可求解静定与超静定问题；
3、线弹性体（线弹性结构）
（1）材料服从胡克定律。 （2）变形微小，各力的作用互不影响。

材料力学第十三章 能量法

材料力学第十三章 能量法

直杆的M0(x)图必定是直线或折线。
M (x)M (x)dx
l
tg x M (x)dx
l
tg xC
MC
M (x) x tg



l
M
(
x)M EI
(x)
dx
M C
EI
顶点 顶点
2lh
3
1lh
3
二次抛物线
例：试用图乘法求所示悬臂梁自由端B的挠度和转角。 解（1）求自由端的挠度
三、弯曲
V W
纯弯曲：
1 2
M
e


1 2
M
e
Mel EI

M e 2l 2EI

M 2l 2EI
横力弯曲：V

l
M 2 (x) dx
2E I ( x)
13-3 变形能的普遍表达式
F3
1
F2
F1
2 3
V
W

1 2
F11
1 2
F2 2

1 2
F3 3

即：线弹性体的变形能等于每一外力与其相应位移乘
例：求图示悬臂梁中点C处的铅垂位移C 。
wC1
B2
F
解：由功的互等定理 F wC1 M B2
F l 2
得：F wC1 M
2 2EI
由此得：
wC1

Ml2 8EI
F3
1
13-5 卡氏定理
F2
F1
2 3 i
V
W

1 2
F11

1 2
F2
2

材料力学13章能量方法习题课

材料力学13章能量方法习题课
当原载荷与单位载荷同时对称于同一根对称轴时我们在写内力方程时可只考虑一半然后将积分结果乘以开口圆环ei为常量ab之间垂直于纸面方向的相对位移内力有几个
R
例1:开口圆环,EI为常量,求AB之间相对水平位移和相对转角 1、求原载荷引起的内力： M ( ) PRSin θ P A 3、求相对转角，施加单位载荷 B P
2、求水平相对位移，施加单位载荷
θ
1 1
θ
1 1
2 AB 0
M ( ) 1
M ( ).M ( ) Rd EI
M ( ) RSin
2 AB 0
在施加单位载荷时 注：用能量法求两点的相对位移时，
一定要在这两个点上同时加一对 大小相等
M ( ).M ( ) Rd EI
Mechanics of Materials
4、积分：
例5：求图示梁的挠曲线方程 P L
解：1、画原载荷引起的内力图
M图 PL 3、画单位载荷引起的内力图
2、求任一点挠度，施加单位载荷 1
x
4、图乘
1
M 图
lx
D
1 (1.M C1 ) EI
l 1 .(l x) 1 1 3 .Pl ) ( .(l x).(l x) . EI 2 l
Pa
5
B
2、求A的水平位移施加单位载荷 C C B
D
A
1
4、图乘：
BA M 图 T 图 M 图 1 1 XA (1.M C1 2 .M C 2 3 .M C 3 4 .M C 4 ) (5 .TC 5 ) EI GI P
DA
B

1 1 1 2a 1 5a 3a ( .Pa.a.0 . pa.a. .2 Pa.a. Pa.a. ) 0 EI 2 2 3 2 3 2

材料力学-第十三章 能量方法

材料力学-第十三章 能量方法

班级学号姓名
１图示桁架各杆的材料相同，截面面积相等。

试求在F力作用下，桁架的应变能。

2计算图示各杆的应变能。

班级学号姓名
3用互等定理求解题。

试求图示各梁的截面Ｂ的挠度和转角，ＥＩ为常数。

4图示刚架的各杆的ＥＩ皆相等，试求截面Ａ，Ｂ的位移和截面Ｃ的转角。

班级学号姓名
5图示桁架各杆的材料相同，截面面积相等。

在载荷Ｆ作用下，试求节点Ｂ与Ｄ间的相对位移。

6图示桁架各杆的材料相同，截面面积相等。

试求节点Ｃ处的水平位移和垂直位移。

班级学号姓名
7刚架各部分的ＥＩ相等，试求在图示一对Ｆ力作用下，Ａ，Ｂ两点之间的相对位移，Ａ，Ｂ两截面的相对转角。

班级学号姓名
8等截面曲杆如图所示。

试求截面Ｂ的垂直位移和水平位移以及截面Ｂ的转角。

9等截面曲杆ＢＣ的轴线为四分之三的圆周。

若ＡＢ杆可视为刚性杆，试求在Ｆ力作用下，截面Ｂ的水平位移及垂直位移。

班级学号姓名
10在图示曲拐的端点Ｃ上作用集中力Ｆ。

设曲拐两段材料相同且均为同一直径的圆截面杆，试求Ｃ点的垂直位移。

11正方形刚架各部分的ＥＩ相等，ＧＩt也相等。

Ｅ处有一切口。

在一对垂直于刚架平面的水平力Ｆ作用下，试求切口两侧的相对水平位移δ。

班级学号姓名
12轴线为水平平面内四分之一圆周的曲杆如图所示，在自由端Ｂ作用垂直载荷Ｆ。

设ＥＩ和ＧＩｐ已知，试求截面Ｂ在垂直方向的位移。

13平均半径为Ｒ的细圆环，截面为圆形，其直径为ｄ。

Ｆ力垂直于圆环中线所在的平面。

试求两个Ｆ力作用点的相对线位移。

第13章- 能量法例题

第13章- 能量法例题

例题9：用图乘法求图示阶梯状梁A截面的 转角及E截面的挠度。
CL12TU40
(1)
(2)
vC1
B2
例题3：长为 l 、直径为 d 的圆杆受一对横向压
力 P 作用，求此杆长度的伸长量。已知E和μ。
例题4：已知简支梁在均布载荷 q 作用下，梁的中
点挠度 f 5q l 4 。求梁在中点集中力P作 384 E I
用下(见图)，梁的挠曲线与梁变形前的轴线所围成的面积 。
§9-4 计算位移的莫尔积分 （单位载荷法）
P1 P2
C
P1 P2
C
M(x)
M 2 (x)
U
l
2E I
dx
P0 1 C
M 0(x)
U 0
l
[ M 0 (x)]2 2E I
dx
P1 P2 P0 C
M(x) + M 0(x)
U1
l
[( M (x) + M 0 (x)]2 2E I
dx
P0 作功： P1、P2 作功：
U0
共做功
U W1 U 0 + U + 1
P0在上又作功：1
P1 P2
P0 1
C
W1 U1
[( M (x) + M 0 (x)]2
U0 +U +1
l
2E I
dx
M 2 (x)
[ M 0 (x)]2
M(x) M 0(x)
l
2E I
dx +
l
2E I
dx +
l
EI
dx
1
l
Ml (Mx()xE)EMMII 00(x()xdx)

材料力学习题册答案-第13章-能量法

材料力学习题册答案-第13章-能量法

第 十三 章 能 量 法一、选择题1．一圆轴在图1所示两种受扭情况下，其（ A ）。

A 应变能相同，自由端扭转角不同；B 应变能不同，自由端扭转角相同；C 应变能和自由端扭转角均相同；D 应变能和自由端扭转角均不同。

（图1）2．图2所示悬臂梁，当单独作用力F 时，截面B 的转角为θ，若先加力偶M ，后加F ，则在加F 的过程中，力偶M （ C ）。

A 不做功； B 做正功；C 做负功，其值为θM ；D 做负功，其值为θM 21。

3．图2所示悬臂梁，加载次序有下述三种方式：第一种为F 、M 同时按比例施加；第二种为先加F ，后加M ；第三种为先加M ，后加F 。

在线弹性范围内，它们的变形能应为（ D ）。

A 第一种大； B 第二种大； C 第三种大； D 一样大。

4．图3所示等截面直杆，受一对大小相等，方向相反的力F 作用。

若已知杆的拉压刚度为，材料的泊松比为μ，则由功的互等定理可知，该杆的轴向变形为EAFlμ，l 为杆件长度。

（提示：在杆的轴向施加另一组拉力F 。

） A 0； BEAFb； a2MMaMCEAFb ； D 无法确定。

F MABCbFF（图2） （图3）二、计算题1．图示静定桁架，各杆的拉压刚度均为相等。

试求节点C 的水平位移。

aaPCBAD解：解法1-功能原理，因为要求的水平位移与P 力方向一致，所以可以用这种方法。

由静力学知识可简单地求出各杆的内力，如下表所示。

()()EAaP EAPa EA Pa P C 22222212222++=∆可得出：()EAPaC122+=∆ 解法2-卡氏定理或莫尔积分，这两种方法一致了。

在C 点施加水平单位力，则各杆的内力如下表所示。

杆i NiNi l i i i l N N ⋅⋅ P 1 a Pa P1 a PaaP 2-2-a 2 Pa 220 0 a1EAPa)222(+则C 点水平位移为：()EAPaC 122+=∆2．图示刚架，已知各段的拉压刚度均为，抗弯刚度均为。

材料力学第十三章 能量法

材料力学第十三章 能量法

1 W F wC 2
由Vε=W 得
Fa 2b 2 wC 3 EIl
例题
试求图示四分之一圆曲杆的变形能,并利用功能原理求B截
B
面的垂直位移. 已知EI为常量.
解： M ( ) FRsin
F
R
θ
M ( ) Vε Rd l 2 EI π ( FRsin )2 πF 2 R 3 2 Rd A 0 2 EI 8 EI 1 W F y 2 πFR 3 由Vε=W 得 y 4 EI
1 1 1 1 W P1 1 P2 2 P3 3 Pn n 2 2 2 2
All forces are applied slowly from zero to the final value. All deformations are within the proportional limit. Conclusion: (1) U is not related to the order in which the forces are applied. (2) U = W
q
A B
F=qa
C x A x B x 2a a
C
1
x
FRA
2a
a
1/2a
（2）求C 截面的转角（在C处加一单位力偶）
qa qx 2 x AB: M ( x) x M ( x) 2 2 2a BC: M ( x ) qa x M ( x) 1 2 2 a qa a 1 qx x C [ ( x )( )dx ( qax )(1)dx ] 0 EI 0 2 2 2a 5qa 3 6 EI （ ）
例题 图示外伸梁,其抗弯刚度为 EI. 用单位载荷法求C点的挠 度和转角.

材料力学 13 能量法

材料力学 13 能量法

P2
U n Pn
U n Pn
第二卡氏定理
意大利工程师—阿尔
n P n
伯托· 卡斯提安诺(Alberto Castigliano， 1847～1884)
二、使用卡氏定理的注意事项：
P1
P2
①U——整体结构在外载作用下的线
弹性变形能 ② Pn 视为变量，结构反力和变形能 等都必须表示为 Pn的函数 ③ n为 Pn 作用点的沿 Pn 方向的变形。
M AB ( x1 ) P( L x1 ) Px ( x x1 )
M BC ( x1 ) P( L x1 )
A
②将内力对Px 求偏导后，令Px=0
M AB ( x) Px 0 x1 x Px
M BC ( x ) Px
Px 0 0
③变形（ 注意：Px=0）
P=60N
B
解：①画单位载荷图
P0 =1 B
A
C
500
A
C x
500xΒιβλιοθήκη 10x120 10 5
②求内力
M AB ( x) Px
M 0 AB ( x ) x
TCA ( x1 ) 0.3P T0CA ( x1 ) 0.3
20
5
M AB ( x) Px
M 0 AB ( x ) x
TCA ( x1 ) 0.3P
EA
Pn
T ( x) T ( x) M ( x) M ( x) dx L dx L dx GI P Pn EI Pn
例5 结构如图，用卡氏定理求A 面的挠度和转角。 P A 解：求挠度，建坐标系 ①求内力 M ( x) xP xP A ②将内力对PA求偏导

材料力学第十三章__能量方法(1)

材料力学第十三章__能量方法(1)

M ()yP(1 R co )s y
I
I
u 12
整理课件
外力所作总余功就等于每个集
中力的余功总和。可写出UC的表达
式如下：
n
UC WC
Pi 0
id P i
i1
表明梁内的余能是作用在梁上一
系列外力Pi的函数.
整理课件
现假设第i个外力Pi有一微小增量dPi，则梁内 余能的变化dUC应为
d UC
UC Pi
d Pi
d 外力U 总C余功d 的变W 化C为此式可d用W 来C计算非id线 P i
整理课件
用功（位移）互等定理关键
1. 找出状态Ⅱ，使状态Ⅱ的外力在（状态Ⅰ） 所求的位移上做功； 2. 状态Ⅱ的外力作用下，（状态Ⅰ）外力作用 点、(状态Ⅰ）外力相应位移容易求出。
P 1 1 2P 2 2 1
整理课件
例：求图示简支梁C截面的挠度。
整理课件
B2
vC1
解：由功的互P等 vC1定 m理 B2
整理课件
∵du=σdε 应变比能
u=∫du =∫εσdε 应变能 U=∫vudv =∫v(∫εσdε)dv
整理课件
功能原理：
物体在外力作用下发生变形，根据 能量守恒定律，当忽略其它能量损 耗时，物体的变形能在数值上等于 外力在加载过程中在相应位移上所
的做功，即U=W
整理课件
(1) 轴向拉伸和压缩
整理课件
力对由自身产生对应位移所
作的功 （线弹性）
W 1 P 力对其它2因素引起对应位移所
作的功。
WP
整理课件
2.应变能（用U或V表示） 在弹性范围内，弹性体在外力作用下发生 变形而在体内积蓄的能量，称为弹性变形 能，简称变形能。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第 十三 章 能 量 法
一、选择题
1．一圆轴在图1所示两种受扭情况下，其（ A ）。

A 应变能相同，自由端扭转角不同；
B 应变能不同，自由端扭转角相
同；
C 应变能和自由端扭转角均相同；
D 应变能和自由端扭转角均不同。

（图1）
2．图2所示悬臂梁，当单独作用力F 时，截面B 的转角为θ，
若先加力偶M ，后加F ，则在加F 的过程中，力偶M （ C ）。

A 不做功； B 做正功；
C 做负功，其值为θM ；
D 做负功，其值为θM 2
1。

3．图2所示悬臂梁，加载次序有下述三种方式：第一种为F 、
M 同时按比例施加；第二种为先加F ，后加M ；第三种为先
加M ，后加F 。

在线弹性范围内，它们的变形能应为（ D ）。

A 第一种大； B 第二种大； C 第三种大； D 一样大。

4．图3所示等截面直杆，受一对大小相等，方向相反的力F 作
用。

若已知杆的拉压刚度为，材料的泊松比为μ，则由功的互等定理可知，该杆的轴向变形为
EA
Fl
μ，l 为杆件长度。

（提示：
在杆的轴向施加另一组拉力F 。

）
A 0；
B EA
Fb ；
C
EA
Fb ； D 无法确定。

（图3）
二、计算题
1．图示静定桁架，各杆的拉压刚度均为相等。

试求节点C 的水
平位移。

解：解法1-功能原理，因为要求的水平位移与P 力方向一致，所以可以用这种方法。

由静力学知识可简单地求出各杆的内力，如下表所示。

(
)()
EA
a
P EA
Pa EA Pa P C 22222212
2
2
2
++=∆
可得出：()
EA
Pa
C
122+=
∆ 解法2-卡氏定理或莫尔积分，这两种方法一致了。

在C 点施加水平单位力，则各杆的内力如下表所示。

则C 点水平位移为：()
EA
Pa
C 122+=
∆
2．图示刚架，已知各段的拉压刚度均为，抗弯刚度均为。

试求
A 截面的铅直位移。

解：采用图乘法，如果不计轴向拉压，在A 点施加单位力，则刚架内力图和单位力图如图所示。

h Fl Fl l h Fl l l Fl EI A 233
1
3221+=⋅⋅+⋅⋅=
∆ 如果考虑轴力影响，则各杆的内力如下表所示。

EA Fh
dx EA F dx EA N N dx EA N N h h BC BC l
AB AB AN
=--+=+=∆⎰⎰⎰202010)1)((0
故A 点总的铅直位移为：
EA
Fh
EI h Fl Fl A ++=∆3323
3．试求图示悬臂梁B 截面的挠度和转角（梁的为已知常数）。

B
解：应用图乘法，在B 点分别加单位力和单位力偶。

它们的内力图如图所示。

⎪⎭⎫ ⎝⎛-=⎪⎭
⎫ ⎝⎛-⋅⋅
=∆4642
313
2
a l qa a l qa a EI B
6
12313
2qa qa a EI B =
⋅⋅=θ
4．图示刚架，已知与。

试用莫尔积分法或图乘法计算B 截面的
垂直位移和转角θB 。

解：应用图乘法，如果不计轴向拉压，在B 点分别加单位力和单位力偶。

它们的内力图如图所示。

852432314
22qa a a qa a qa a EI B =
⋅⋅+⋅⋅=∆
3
21212313
22qa a qa qa a EI B =
⋅⋅+⋅⋅=θ
如果考虑轴向拉压，解法同第2题，略。

5．如图所示刚架受一对平衡力F 作用，已知各段的相同且等于
常量，试用图乘法求两端A 、B 间的相对转角。

Fa
B
A
Fa
Fa
1
1
解：应用图乘法，在A 、B 点加一对单位力偶。

它们的内力图如图所示。

221212
1
Fa a Fa a Fa EI AB =⋅⋅+⋅⋅⋅=
θ
6．图示刚架，已知各段的抗弯刚度均为。

试计算B 截面的水平
位移和C 截面的转角。

P
A
Pl Pl-M
解：应用图乘法，在B 截面加一水平单位力，在C 截面加一单位力偶，它们的内力图如图所示。

()2331
232213221Ml Pl l l M Pl l l Pl l l Pl EI B -=⋅⋅-+⋅⋅+⋅⋅=∆ ()()l M Pl l M Pl EI AB
-=⋅⋅-=3
1
3221θ。