cardinal曲线
- 格式:pdf
- 大小:60.42 KB
- 文档页数:3
我们已经详细介绍过低次(二次、三次)的Hermite 插值样条,它是基于端点的位置矢量和曲线在两端点的切矢建立的,但有时候我们不需要输入曲线斜率值或其他几何信息就能生成样条曲线,因此就出现了Cardinal 样条,这种基于Hermite 样条的变化形式,它不需要输入曲线控制点上的导数值,而是采用控制点的坐标位置来计算导数。
下面我们来详细介绍一下Cardinal 样条Cardinal 样条跟Hermite 样条一样,也是分段三次插值样条,一段Cardinal 样条曲线完全由4个连续的控制点给出。
中间两个控制点是曲线端点,另外两个控制点用来计算终点斜率。
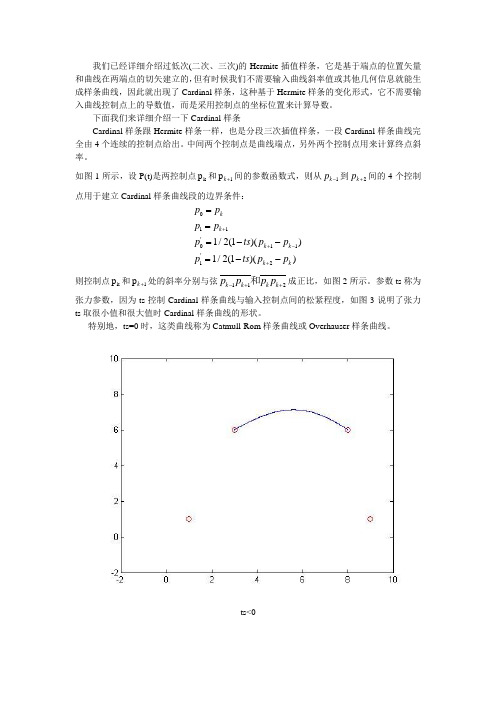
如图1所示,设P(t)是两控制点k p 和1p k +间的参数函数式,则从1k p -到2k p +间的4个控制点用于建立Cardinal 样条曲线段的边界条件:011'011'121/2(1)()1/2(1)()kk k k k k p p p p p ts p p p ts p p ++-+===--=--则控制点k p 和1p k +处的斜率分别与弦112k k k k p p p p -++和成正比,如图2所示。
参数ts 称为张力参数,因为ts 控制Cardinal 样条曲线与输入控制点间的松紧程度,如图3说明了张力ts 取很小值和很大值时Cardinal 样条曲线的形状。
特别地,ts=0时,这类曲线称为Catmull-Rom 样条曲线或Overhauser 样条曲线。
ts<0Ts>0将上面的4个方程代入三次Hermite样条曲线的方程,并将之转换成矩阵形式,如下:(2)其中, Cardinal矩阵是:(3)其中s = (1 - ts) / 2将矩阵方程(2)展开成多项式形式,可以得到P(u) = P k-1(-su3+ 2su2 - su) + P k[(2 - s)u3 + (s - 3)u2 + 1] + P k+1[(s - 2)u3 + (3 – 2s)u2 + su] + P k+2(su3 - su3)。



关于三次B样条曲线重构中射影变换及控制点反求的一点思考王娟【摘要】It is proved that the cubic B-spline curve is still cubic B-spline curve after projective trans-formation.It is proposed that cubic B-spline curves in the image plane are the projective of cubic B-spline curves in space.The projective relations between the control points of the cubic B-spline curves in the image plane and the cubic B-spline curves in space are given.A method of solving B-spline curve control points is proposed.%证明了三次B样条曲线经过射影变换后仍然是三次B样条曲线;提出了像平面中三次B样条曲线是空间中三次B样条曲线的射影;给出了像平面中三次B样条曲线控制点与空间中三次B样条曲线控制点的射影关系;提出了B样条曲线控制点的反求方法。
【期刊名称】《昆明冶金高等专科学校学报》【年(卷),期】2016(032)005【总页数】4页(P73-75,84)【关键词】射影变换;控制点;反求;三维重构【作者】王娟【作者单位】云南锡业职业技术学院学生处,云南个旧661000【正文语种】中文【中图分类】TP391.9样条曲线是指由给定的控制点得到曲线,曲线的大致形状由这些点予以控制[1]。
常见的样条曲线有:Hermite样条、Cardinal样条、Kochanek-Bartels样条、Bezier样条、B样条、非均匀有理B样条曲线(NURBS)。


1、绝对优势(Absoluteadvantage)如果一个国家用一单位资源生产的某种产品比另一个国家多,那么,这个国家在这种产品的生产上与另一国相比就具有绝对优势。
2、逆向选择(Adversechoice)在此状况下,保险公司发现它们的客户中有太大的一部分来自高风险群体。
3、选择成本(Alternativecost)如果以最好的另一种方式使用的某种资源,它所能生产的价值就是选择成本,也可以称之为机会成本。
4、需求的弧弹性(Arcelasticityofdemand)如果P1和Q1分别是价格和需求量的初始值,P2和Q2为第二组值,那么,弧弹性就等于-(Q1-Q2)(P1+P2)/(P1-P2)(Q1+Q2)5、非对称的信息(Asymmetricinformation)在某些市场中,每个参与者拥有的信息并不相同。
例如,在旧车市场上,有关旧车质量的信息,卖者通常要比潜在的买者知道得多。
6、平均成本(Averagecost)平均成本是总成本除以产量。
也称为平均总成本。
7、平均固定成本(Averagefixedcost)平均固定成本是总固定成本除以产量。
8、平均产品(Averageproduct)平均产品是总产量除以投入品的数量。
9、平均可变成本(Averagevariablecost)平均可变成本是总可变成本除以产量。
10、投资的β(Beta)β度量的是与投资相联的不可分散的风险。
对于一种股票而言,它表示所有现行股票的收益发生变化时,一种股票的收益会如何敏感地变化。
11、债券收益(Bondy ield)债券收益是债券所获得的利率。
12、收支平衡图(Break-evenchart)收支平衡图表示一种产品所出售的总数量改变时总收益和总成本是如何变化的。
收支平衡点是为避免损失而必须卖出的最小数量。
13、预算线(Budgetline)预算线表示消费者所能购买的商品X和商品Y的数量的全部组合。
它的斜率等于商品X的价格除以商品Y的价格再乘以一1。
金属电极的极化曲线介绍金属电极的极化曲线是描述金属电极在不同电位下电流与电势之间关系的曲线。
通过研究金属电极的极化曲线,可以了解电极在电化学反应中的行为特性,对电化学领域的研究具有重要意义。
极化曲线的构成极化曲线通常由电流密度(i)和电势(E)之间的关系图示形成。
E轴表示电势,i轴表示电流密度。
在实验中,通过改变电势的值,测量相应的电流密度,得到一系列的数据点,从而绘制出金属电极的极化曲线。
极化曲线的类型1. 极化曲线的基本形状金属电极的极化曲线一般呈现出以下几种基本形状:(1) 直线形直线形极化曲线通常表示电极处于在低电流密度下的平稳状态。
在这种状态下,电极的电化学反应速率与电势之间存在线性关系。
(2) 曲线形曲线形极化曲线通常表示电极发生了某种非均匀的极化过程。
这种非均匀的极化可能是由于电极表面发生了物理或化学变化,导致电化学反应速率与电势的关系不再是线性的。
(3) 反S形反S形极化曲线通常表示电极出现了过渡性的行为。
在某个特定的电势区间内,电极的电化学反应速率明显变化,呈现出S形曲线的倒置。
2. 极化曲线的特征金属电极的极化曲线具有以下几个特征:(1) 线性段极化曲线的线性段通常是在电流密度较低的区域。
在这个区域内,电极的电化学反应速率与电势之间存在着线性关系。
(2) 饱和段极化曲线的饱和段通常是在电流密度较高的区域。
在这个区域内,电极的电化学反应速率已经饱和,不再随电势的增加而增加。
(3) 极化电势极化曲线上的极化电势是指电流密度为零时对应的电势值。
极化电势可以反映电极的活性和稳定性。
(4) 极化电阻极化曲线上的极化电阻是指电流密度与电势之间斜率的倒数。
极化电阻越大,说明电极的极化程度越高。
极化曲线的应用1. 材料研究通过分析金属电极的极化曲线,可以评估材料的耐蚀性和抗氧化性能。
这对于材料的选择和设计具有重要意义。
2. 腐蚀研究金属电极的极化曲线可用于研究金属在不同环境条件下的腐蚀行为和机理。
基于三次Cardinal样条曲线的航线平滑作者:缪永飞吴北苹吕健来源:《电脑知识与技术》2015年第25期摘要:根据优化算法生成的航线由多个航线点顺序连接所形成的航段序列表示,其规划结果具有引导作用,但不具可飞性。
该文引入三次Cardinal样条曲线对航线进行平滑,注重介绍了三次Cardinal样条曲线的基本原理,结合无人机航线规划的特点,提出了具体的航线平滑方法。
关键词:航线平滑;Cardinal样条曲线;张力系数中图分类号:TP302 文献标识码:A 文章编号:1009-3044(2015)25-0160-011无人机航线规划的特点随着信息化战争的发展,无人机将在未来一体化战争中扮演越来越重要的角色。
航线规划是指根据无人机的任务目标规划满足约束条件的飞行轨迹,它要求无人机根据飞行环境在适当的时间内计算出最优或者次优的飞行轨迹,并能够回避敌方威胁,适时进行飞行轨迹的动态修正。
它是无人机集群配合、战术规划和智能自主飞行的技术基础。
航线生成往往采用智能算法,如遗传算法[1]、免疫算法、A*算法、粒子群算法[2]等,生成空间连续的航迹点的过程。
航线生成是航线规划算法优劣、航线质量评估的基础。
以往的航线平滑算法多利用B样条曲线等线性插值方法[3],这种方法的优点是算法复杂度底、计算简单,但也存在一、二阶不连续可导的不足。
2 三次Cardinal样条曲线的基本原理Cardinal样条是插值分段三次曲线,并且每条曲线段的终点位置均指定切线,不过Cardinal样条不用给出终点的切线值。
在Cardinal样条中,一个控制点的斜率可以由两个相邻控制点的坐标进行计算[4]。
Cardinal样条可由4个连续控制点完全确定,中间2个控制点是曲线段端点,其他两个点用于计算曲线段端点斜率。
3 结束语随着无人机承担任务的复杂性的不断提高及飞行环境的不确定性,对无人机航线规划的要求也越来越高。
而作为航线规划中比较关键的航线平滑技术,是无人机高效遂行未来全方位多机协同任务的重要保证和技术基础。