相交平面的画图技法

知识点平面几何中的相交线与平面在平面几何中，相交线与平面是一个重要的知识点。

相交线与平面的关系可以帮助我们理解和解决许多几何问题。

在本文中，我将介绍相交线与平面的定义、性质和应用。

通过学习本文，读者将能够更好地理解和应用平面几何中的相交线与平面。

一、相交线与平面的定义在几何学中，我们将线段或直线与平面的交点称为相交线。

相交线可以是线段的一部分，也可以是直线的一部分。

二、相交线与平面的性质1. 交点个数：一条直线可以与一个平面相交于一点，也可以与一个平面相交于无穷多个点。

如果一条直线不在平面上，那么它和这个平面没有交点。

2. 平面内部：一条直线在平面内部的一部分被称为直线在平面上。

一条直线可以在平面内部上下延伸到无穷远。

3. 平面内平行线：如果两条直线在同一个平面上，且这两条直线不相交，那么它们被称为平面内平行线。

4. 平面内垂直线：如果一条直线与平面上的另一条直线垂直，且与平面的交点在这条直线的任意一点上，那么这条直线被称为平面内垂直线。

三、相交线与平面的应用相交线与平面的性质可以应用于许多实际问题和几何证明中。

1. 直线与平面的交点问题：当我们需要确定一条直线与一个平面的交点时，可以利用相交线与平面的定义和性质来解决。

例如，我们可以通过求解一个方程组的方法来确定一条直线与一个平面的交点坐标。

2. 平行线问题：当我们需要确定两条直线在平面上是否平行时，可以利用相交线与平面的定义和性质来判断。

如果两条直线与同一个平面的交点个数为零，那么这两条直线即平行。

3. 垂直线问题：当我们需要确定一条直线与一个平面上的另一条直线是否垂直时，可以利用相交线与平面的定义和性质来判断。

如果一条直线与一个平面上的直线垂直，那么这条直线与平面的夹角为90度。

4. 三角形问题：在三角形的研究中，相交线与平面的概念也有着广泛的应用。

例如，我们可以利用相交线与平面的性质来证明三角形的内角和为180度，或者用于解决三角形面积计算等问题。

平面与平面的交线平面与平面的交线是几何学中的一个重要概念，它描述了两个平面相交所形成的线段。

在本文中，我们将探讨平面与平面的交线的定义、性质、示例以及在实际应用中的意义。

一、定义平面是由无数个平行的直线组成的，而平面与平面的交线是两个平面相交所形成的线段。

交线可以是一条直线，也可以是多条线段组成的曲线。

平面与平面的交线可以分为三种情况：无交线、一个交线和无数个交线。

二、性质1. 平行平面：两个平行平面之间不存在交线，因为它们永远不会相交。

2. 切平面：当一个平面与另一个平面相切时，它们的交线是一条直线。

3. 相交平面：当两个平面相交于一点时，它们的交线是无数个直线，这些直线都经过相交点。

4. 垂直于平面的直线：如果一条直线与一个平面相交，而且与这个平面的交线垂直，那么这条直线与平面的交线是一条直线。

三、示例1. 两个相互垂直的平面：考虑一个立方体，底面和一个侧面之间的交线是一条直线。

2. 两个相交的平面：考虑一个圆柱体，底面和侧面之间的交线是一个圆。

3. 平行平面：考虑两个平行的墙壁，它们之间不存在交线。

四、实际应用平面与平面的交线在实际应用中有着广泛的应用。

以下是其中几个常见的应用示例：1. 建筑设计：在建筑设计中，平面与平面的交线可以帮助建筑师确定建筑物之间的空间关系，例如墙壁与屋顶的交线可以决定房间的高度和倾斜角度。

2. 汽车设计：在汽车设计中，平面与平面的交线可以帮助设计师确定车身的曲线和车窗的形状，以及车门和车顶的连接线。

3. 机械制造：在机械制造中，平面与平面的交线可以帮助工程师确定零件的装配方式，以及各个零件之间的相对位置和运动轨迹。

4. 地理测量：在地理测量中，平面与平面的交线可以帮助测量师确定地面的高度和地表的曲率，以及山脉与河流的交汇点。

综上所述，平面与平面的交线是几何学中的重要概念，它描述了两个平面相交所形成的线段。

我们通过定义、性质、示例和实际应用，对平面与平面的交线进行了详细的说明。

立体几何中直线与平面相交的经典方法+经典题(附详细解答)在立体几何中，直线和平面的相交问题是常见的问题。

本文将介绍两种经典的方法解决直线和平面的相交问题，并附上练题和详细解答。

方法一：截距法截距法是利用平面直角坐标系的思想来解决立体几何中直线和平面的相交问题。

步骤如下：1. 将空间直线的参数方程化成对应的参数式，例如设直线为$L:\begin{cases} x=x_0+ua\\ y=y_0+ub\\ z=z_0+uc\end{cases}(u\in\mathbb{R})$；2. 将空间平面的一般式化为标准式，例如设平面为 $\pi:Ax+By+Cz+D=0$；3. 将直线的参数式带入平面的一般式中，得到一个关于参数$u$ 的一元二次方程；4. 解出该方程的 $u$ 值，代入直线的参数式中，即可得到直线与平面的交点。

方法二：向量法向量法是利用向量的点乘和叉乘来解决立体几何中直线和平面的相交问题。

步骤如下：1. 将空间直线的参数方程化成对应的点向式，例如设直线为$L: \bold{r}= \bold{a} + \lambda \bold{b}$；2. 将空间平面化为法向量的点法式，例如设平面为$\pi:\bold{n}\cdot\bold{r}+d=0$；3. 将直线的点向式代入平面的点法式中，得到一个关于参数$\lambda$ 的一元一次方程；4. 解出该方程的 $\lambda$ 值，代入直线的点向式中，即可得到直线与平面的交点。

经典题1. 已知直线 $L: \begin{cases} x=1+2t \\ y=t \\ z=2-3t \end{cases}$，平面 $\pi: 2x+y-2z=3$，求它们的交点。

解：应用截距法，将直线的参数方程化为：$$\begin{cases}x=1+2t \\ y=t \\ z=2-3t \end{cases}=\begin{cases} x=1 \\ y=0 \\ z=2\end{cases}+t \begin{cases} 2 \\ 1 \\ -3 \end{cases}$$将平面的一般式化为标准式，得到：$\pi: x+\frac{1}{2}y-z-\frac{3}{2}=0$。

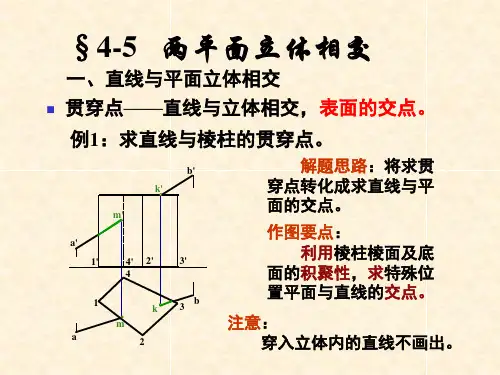
相交平面的画图技法
平面的画法是学习立体几何的最初知识，也是基础知识．相交平面的画图是平面画图的重要内容，本文介绍两种常见的画法．
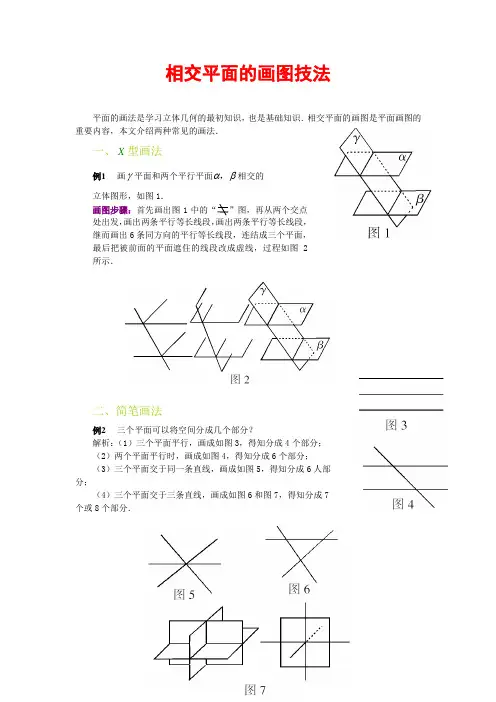
一、X型画法
例1画γ平面和两个平行平面αβ
，相交的
立体图形，如图1．
画图步骤：首先画出图1
中的“”图，再从两个交点
处出发，画出两条平行等长线段，画出两条平行等长线段，
继而画出6条同方向的平行等长线段，连结成三个平面，
最后把被前面的平面遮住的线段改成虚线，过程如图2
所示．
二、简笔画法
例2三个平面可以将空间分成几个部分？
解析：（1）三个平面平行，画成如图3，得知分成4个部分；
（2）两个平面平行时，画成如图4，得知分成6个部分；
（3）三个平面交于同一条直线，画成如图5，得知分成6人部分；
（4）三个平面交于三条直线，画成如图6和图7，得知分成7个或8个部分．
（注：专业文档是经验性极强的领域，无法思考和涵盖全面，素材和资料部分来自网络，供参考。

可复制、编制，期待你的好评与关注）。

Word怎么绘制相交平面图
在立体几何教学中，有关两个平面相对位置的绘图是比较多的。

下面就如何在Word 2000中快速绘制相交平面图介绍一下笔者的画法。

1.在“绘图”工具栏的“自选图形/基本形状”中选择“平行四边形”，用它画两个平面，且相交。

调整好两平面的位置，并用直线工具画一条平面相交线。

2.将被遮挡的部分画成虚线。

利用直线工具画两条线段，长度与被遮挡线段等长，并将其完全覆盖。

从工具栏上的线型列表中，将所画线段设置为虚线。

此时因为虚线下面是实线，所以看上去还是实线。

双击虚线，打开“设置自选图形格式”对话框，在“线条与颜色”选项卡中将“线条”颜色设置为“白色”，确认退出。

现在你再瞧，遮挡部分变成虚线了吧。

提示：此时虚线看上去有点模糊，为获得最佳效果，可将虚线设置得比实线宽一点。

如实线是0.75磅，虚线可设置为1.5磅，这样效果就非常好了。

3.若要给平面加上标注（如α、β），可先插入一个文本框，对文本框进行如下设置：双击文本框，打开“设置文本框格式”对话框，在“线条与颜色”选项卡中将“线条”颜色设置为“无线条颜色”，并在“填充”中将“透明度”设置为100%。

然后在文本框中输入字母。

最后把全部对象选中，组合在一起。

如果您使用的是Word XP，在开始绘图时把图形画在画布内，完成后不需组合。

这样一个规范的平面相交图形就快速绘制完成了。

空间几何中的相交平面问题相交平面问题是空间几何中一个重要的概念和研究方向。

它涉及到平面的交叉、相交及其相关的性质和应用。

在本文中，我们将探讨相交平面问题在空间几何中的应用和解决方法。

1. 平面的定义与性质在空间几何中，平面是由无限多个点组成的，且任意两点之间的连线都在平面上的图形。

平面有以下性质：（1）平面内的任意三点不共线；（2）经过平面上的两点可以确定一条直线；（3）平面上的任意两条直线要么相交于一点，要么平行。

2. 平面的相交问题当两个平面相交时，它们通常会形成一条直线。

根据两个平面的相对位置，我们可以得到以下几种情况：（1）相交于一条直线：当两个平面不平行且不重合时，它们会相交于一条直线。

这种情况常见于交错的切割面和多面体的边界。

（2）平行：当两个平面无交点时，它们被称为平行。

平行平面可以在工程和建筑中发挥重要作用，例如平行的墙面。

（3）重合：当两个平面完全重合时，它们被称为重合。

这意味着它们所有的点都是重合的，可以互相替换使用。

3. 直线与平面的关系直线与平面之间的关系也是相交平面问题的一个重要方面。

根据直线和平面的相对位置，我们可以得到以下几种情况：（1）直线与平面相交：当一条直线与平面相交时，它们通常会交于一点。

这点称为直线在平面上的投影点。

（2）直线在平面上：当一条直线完全位于平面上时，我们称其为直线在平面上。

直线在平面上的性质可以用来求解许多几何问题。

（3）直线与平面平行：当一条直线与平面不存在交点时，我们称其为直线与平面平行。

这是一个重要的特殊情况，常见于平行投影和切线问题。

4. 相交平面的应用相交平面问题不仅在数学中有重要应用，还广泛应用于其他领域，如物理、工程和计算机图形学等。

下面以一些应用场景为例进行介绍：（1）画家的透视法：绘画中的透视法是基于相交平面的原理进行构图和绘制的技巧。

通过合理运用相交平面的性质，画家可以实现真实感和立体感。

（2）建筑设计：在建筑设计中，相交平面问题被广泛用于结构分析和空间布局。

平面与平面的交点计算方法在几何学中，平面与平面的交点是一个重要的概念。

计算平面与平面的交点可以帮助我们解决各种实际问题，例如建筑设计、机械制图等。

在本文中，我们将介绍几种常用的计算平面与平面交点的方法。

方法一：代数法平面可以由一个点和一个法向量来表示。

当两个平面相交时，它们的交线也是两个平面的交点。

我们可以使用代数方法来计算平面与平面的交点。

设平面1的方程为A1x + B1y + C1z + D1 = 0，平面2的方程为A2x + B2y + C2z + D2 = 0。

其中A1、B1、C1、D1分别是平面1的系数，A2、B2、C2、D2分别是平面2的系数。

首先，我们需要计算两个平面的法向量。

平面1的法向量为 (A1,B1, C1)，平面2的法向量为 (A2, B2, C2)。

然后，我们可以计算两个平面的交线的方向向量。

交线的方向向量为两个平面的法向量的叉乘。

设交线的方向向量为 (p, q, r)。

接下来，我们需要找到交点的一个具体示例。

我们可以假设一个点在平面2上，然后计算该点在平面1上的投影点，即交点。

我们可以通过代入平面2的方程，解得该点的坐标，即x = x0 + tp，y = y0 + tq，z = z0 + tr，其中 (x0, y0, z0) 是在平面2上任意选取的一点，t 是实数。

将求得的坐标代入平面1的方程，我们可以得到交点的坐标。

方法二：几何法几何法是一种图形推导的方法，通过直观的方式计算平面与平面的交点。

我们可以首先确定两个平面的交线。

然后，我们选择两个平面的一个交线上的两点，分别代入两个平面的方程，得到一组方程组。

解方程组可以得到交点的坐标。

假设两个平面的方程分别为Ax + By + Cz + D1 = 0和Ex + Fy + Gz+ D2 = 0。

首先，我们需要确定两个平面的交线方程。

选择一组点坐标表示交线上的一点，例如 (x0, y0, z0) 和 (x1, y1, z1)。

平面几何的相交与切线在平面几何的研究中，相交和切线是两个重要的概念。

相交是指两个或多个几何图形在平面上有交集的情况，而切线是指一条直线与曲线在某一点处刚好接触的情况。

本文将介绍相交与切线的基本概念、性质以及应用，并通过一些实例来加深理解。

一、相交相交是指两个或多个几何图形在同一平面上有交集。

相交的图形可以是线段、直线、曲线、多边形等。

具体来说，相交有以下几种情况：1. 线段相交：当两个线段在同一平面上有交集时，它们被称为相交线段。

若线段AB与线段CD相交于点E，则有以下几种情况：线段AB与线段CD仅有一个公共点E，此时称线段AB与线段CD相交；线段AB在一部分上与线段CD重合，此时也称两线段相交。

2. 直线相交：当两条直线在同一平面上有交点时，它们被称为相交直线。

若直线L1与直线L2相交于点P，则L1和L2相交。

3. 曲线相交：当两条曲线在同一平面上有交点时，它们被称为相交曲线。

例如，两个圆在同一个平面上有两个相交点时，它们被称为相交圆。

在相交的研究中，我们常常关注相交的位置、数量以及相交角等特性。

通过研究相交的性质，我们可以推导出一些几何定理，为后续的几何推理提供基础。

二、切线切线是一条直线与曲线在某一点相切的情况。

当一条直线与曲线在某一点处只有一个公共点，并且与曲线的切线重合时，我们称该直线为曲线的切线。

切线的特点是与曲线在切点处垂直。

对于圆的切线而言，切线与半径的夹角为直角。

而对于非圆曲线来说，切线与曲线的切点处切线的斜率等于曲线在该点切线的斜率。

切线在几何学中有广泛的应用，例如在物体约束、最优路径问题中的运用等。

三、相交与切线的应用1. 空间布局：相交和切线的概念在空间布局中有着重要的应用。

例如在建筑设计中，我们可以通过相交的墙体来定义房间的位置和形状；在道路交通规划中，交叉口的设计需要考虑不同道路相交的情况。

2. 计算几何：相交和切线的概念在计算几何学中有广泛的应用。

例如，在计算机图形学中，我们可以通过相交来判断两个图形是否重叠；在路径规划中，我们可以通过计算曲线与直线的切点来确定最优路径。

两曲面相交曲线的法平面
两曲面相交时，可以确定一条曲线，这条曲线上的每一点都同时位于两个曲面上。

在这个问题中，我们需要找到曲线上某一点的法平面。

法平面是垂直于曲线的平面，它通过曲线上某一点，并且与曲线的切线垂直。

为了找到曲线上某一点的法平面，我们可以按照以下步骤进行：
1. 找到曲线上的一点，我们可以通过给定的参数方程或者隐式方程，找到曲线上的一个点。

假设这个点的坐标为(x0, y0, z0)。

2. 求得曲线的切向量，我们可以对曲线的参数方程求导或者通过隐式方程进行计算，得到曲线在这一点上的切向量。

假设切向量为T = (Tx, Ty, Tz)。

3. 求得曲线的法向量，由于曲线上的点同时位于两个曲面上，所以曲线的切向量也同时垂直于两个曲面的法向量。

假设两个曲面的法向量分别为N1 = (N1x, N1y, N1z)和N2 = (N2x, N2y, N2z)。

则曲线的法向量可以通过两个曲面的法向量的叉积得到，即N = N1
x N2。

4. 求得法平面方程，由于法平面通过曲线上的一点，我们可以
利用该点的坐标和法向量来确定法平面的方程。

假设法平面的方程
为Ax + By + Cz + D = 0，则根据点法式，我们可以得到A = Nx，
B = Ny，
C = Nz，
D = -(Nx x0 + Ny y0 + Nz z0)。

综上所述，我们可以通过以上步骤找到曲线上某一点的法平面。

需要注意的是，如果两个曲面在某一点上的切向量平行或者曲线上
的点不满足同时位于两个曲面上的条件，那么该点可能不存在法平面。

浅谈两相交平面交线的求法.doc
两相交平面交线是指两个相交的平面L1和L2在空间内所形成的交线，它是求解空间
平面几何问题的重要技术。

求取两相交平面交线的方法有以下几种：
一、零点法。

这种方法的思路是，根据两相交平面的参数方程，将其恒等式的两边拆
分出来，然后把它们重新组合，使其等于零，即有：ax＋by＋cz ＋d＝0，这样可以获得
一组“零点”，即x＝-bc/a，y ＝-ac/b，z ＝-ad/c，它们就是平面L1和L2的交线参数方程的解。

二、投影法。

这是一种用视图法在建模中表示两相交平面交线的方法，它利用几何上
的直观理解，在建模时从一个平面投影到另一个平面上，再将其投影回来，然后解析其交点，即可求得两相交平面的交线参数方程的解。

三、矢量法。

这是一种利用向量分析法在建模中表示两相交平面交线的方法，它首先
将向量法叙述的参数方程，也就是：
(x-x0)w1+(y-y0)w2+(z-z0)w3=0
其中x0、y0、z0为L1平面和L2平面的三个点，w1、w2、w3为L1和L2平面分别对
应的向量，这样根据解向量方程解出它们的解，即可求得两相交平面的交线参数方程的解。

以上就是关于求取两相交平面交线的几种方法，综上所述，可以看出，求取两相交平
面的交线的最重要的技术之一就是不同的参数方程。

如果要得出满意的结果，就需要熟练
掌握这些参数方程的求解方法，以此来解决例如坐标转换和空间参数拟合等多种复杂计算
问题。

平面与平面之交线平面与平面的交线是几何学中的一个重要概念。

当两个平面相交时，它们通常会形成一条直线，这条直线被称为交线。

交线的定义交线是两个平面相交形成的一条直线。

平面可以通过其上的两个点和法线方向来确定。

当两个平面相交时，它们的交线将是这两个平面共有的所有点构成的直线。

交线的性质交线有一些重要的性质需要注意：1. 交线是共有的：当两个平面相交时，它们的交线上的所有点都属于这两个平面。

2. 交线是直线：当两个平面相交时，它们的交线将是一条直线，而不是弯曲的形状。

3. 交线是无限的：两个平面相交的点有无数个，因此它们的交线也是无限延伸的。

如何确定交线确定两个平面的交线可以通过以下几个步骤进行：1. 确定两个平面的方程：根据给定的信息，可以确定两个平面的方程。

2. 解方程组：将两个平面的方程联立，解方程组可以找到它们的交线的参数表示。

3. 确定交线的参数表示：通过解方程组得到的参数解，可以确定交线的参数表示。

4. 绘制交线：根据参数表示，可以绘制出交线在平面上的形状。

交线的应用平面与平面的交线在几何学和工程学中有广泛的应用。

一些典型的应用包括：1. 切割物体：当我们需要将一个物体切割成两个部分时，可以利用平面与平面的交线来确定切割面。

2. 交通规划：在交通规划中，平面与平面的交线可以用来描述不同道路、铁路或飞行轨迹的相交情况。

3. 机械设计：在机械设计中，交线的概念可以用来描述不同平面的相对位置和运动。

以上是关于平面与平面之交线的简要介绍。

通过了解交线的定义、性质和确定方法，我们可以更好地理解和应用这一概念。