数学知识点新人教版数学2015-2016学年度第一学期二年级期末试卷(1)-总结

2014-2015学年度第一学期二年级数学期末试卷得分___________ 一、我会口算（共10分）72－8= 5×9= 36－9= 57+9= 30+70=76－40= 8×4= 7×5= 70－7= 35+8=9+44= 5×4= 9×6= 24－7= 3×8=7×8－20＝ 4×9＋4＝ 32－20+50＝ 7－3×2＝二、我会填。

（每空一分，共28分）1.）在括号里填上适当的单位名称。

①一张床长约200（）②长颈鹿高约3（）③一本语文课本厚约2（）④一座楼房高12（）⑤小学生每天在校时间是6 （）。

⑥看一场电影的时间是120（）。

2.）小丽的身高是83厘米，小兵身高1米，小丽比小兵矮（）厘米。

3.）7+7+7+7=（）写成乘法算式是（）读作( ）；4.）两个乘数都是8，积是（）。

5.）你能用0 、 3 、 5 这三张数字卡片组成（）个不同的两位数，其中最大的数是（），最小的数是（），它们相差（）。

6.）2和7的和是（）2个7的和是（），2个7的积是（）7.）8.）在○里填上“﹥”、“﹤”或“=”。

26○17+18 31﹣8○3×7 100厘米○98米9.）括号里最大能填几？8×（）＜60 42＞（）×6 27＞4×（）（）×5＜36 70＞9×（）（）×3＜22三、我会选（将正确答案的序号填在括号里）（每题1分，共5分）1.）4个3列成加法算式是（）。

①3+3+3+3 ②4+4+4 ③4×32.）明明有3件不同的衬衣，2条颜色不一样的裙子，一共有（）种穿法。

①5 ②6 ③33.）下列图形中，有二个直角的是（）。

①②③④4.）下列线中，线段是（）。

①②③④5.）可以用测量物体长度单位的是（）。

①时②角③分④米四、我会用竖式计算。

2015-2016高一上学期期末复习知识点与典型例题人教数学必修一 第二部分 函数1、函数的定义域、值域2、判断相同函数3、分段函数4、奇偶性5、单调性1．定义域 值域（最值） 1．函数()()3log 3f x x =++的定义域为____________________ 2．函数22()log (23)f x x x 的定义域是（ ）(A) [3,1] (B) (3,1) (C) (,3][1,)-∞-+∞ (D) (,3)(1,)-∞-+∞3．2()23,(1,3]f x x x x =-+∈-的值域为____________________ 4．若函数21()2f x x x a =-+的定义域和值域均为[1,](1)b b >，求a 、b 的值．2．函数相等步骤：1、看定义域是否相等； 2、看对应关系（解析式）能否化简到相同1．下列哪组是相同函数？2(1)(),()x f x x g x x ==(2)()()f x x g x ==,2(3)()2lg ,()lg f x x g x x ==(4)(),()f x x g x ==3．分段函数基本思路：分段讨论 （1）求值问题1．24(),(5)(1)4xx f x f f x x ⎧<==⎨-≥⎩已知函数则_______________ 2．设函数211()21x x f x x x⎧+≤⎪=⎨>⎪⎩，则=))3((f f ______________（2）解方程1．2log ,11(),()1,12x x f x f x x x >⎧==⎨-≤⎩已知函数则的解为_________________2．已知⎩⎨⎧>-≤+=)0(2)0(1)(2x x x x x f ，若()10f x =，则x = .（3）解不等式1．21,0(),()1,0x f x f x x x x ⎧>⎪=>⎨⎪≤⎩已知函数则的解集为__________________2．2log ,0(),()023,0x x f x f x x x >⎧=>⎨+≤⎩已知函数则的解集为__________________（4）作图、求取值范围（最值）1．24-x ,0()2,012,0x f x x x x ⎧>⎪==⎨⎪-<⎩已知函数．（1）作()f x 的图象；（2）求2(1)f a +，((3))f f 的值；（3）当43x -≤＜，求()f x 的取值集合（5）应用题（列式、求最值）1．为方便旅客出行，某旅游点有50辆自行车供租赁使用，管理这些自行车的费用是每日115元．根据经验，若每辆自行车的日租金不超过6元，则自行车可以全部租出；若超过6元，则每超过1元，租不出去的自行车就增加3辆，为了便于结算，每辆自行车的日租金x(元)只取整数，并且要求出租自行车一日的总收入必须高于这一日的管理费用，用y (元)表示出租自行车的日净收入(即一日中出租自行车的总收入减去管理费用后的所得)， （1）求函数f(x)的解析式及其定义域；（2）试问当每辆自行车的日租金定为多少元时，才能使一日的净收入最多？4．函数的单调性（1）根据图像判断函数的单调性——单调递增：图像上升 单调递减：图像下降 1．下列函数中，在区间(0,)+∞上为增函数的是（ ）A ．ln(2)y x =+ B．y =．1()2xy = D ．1y x x=+2．下列函数中，在其定义域内为减函数的是（ ）A ．3y x =- B ．12y x = C ．2y x = D ．2log y x =（2）证明函数的单调性步骤——取值、作差12()()f x f x -、变形、定号、下结论 1．已知函数11()(0,0)f x a x a x=->>． (1)求证：()f x 在(0,)+∞上是单调递增函数；(2)若()f x 在1[,2]2上的值域是1[,2]2，求a 的值．（3）利用函数的单调性求参数的范围1．2()2(1)2(2]f x x a x =+-+-∞在，上是减函数，则a 的范围是________2．若函数⎪⎩⎪⎨⎧<-≥-=2,1)21(,2,)2()(x x x a x f x 是R 上的单调递减函数，则实数a 的取值范围为（ ）A ．)2,(-∞B ．]813,(-∞ C ．)2,0( D ．)2,813[3．讨论函数223f(x)x ax =-+在(2,2)-内的单调性（4）利用函数的单调性解不等式1．()f x 是定义在(0,)+∞上的单调递增函数，且满足(32)(1)f x f -<，则实数x 的取值范围是（ ） A ． (,1)-∞ B ． 2(,1)3 C ．2(,)3+∞ D ． (1,)+∞ 2．2()[1,1](1)(1)f x f m f m m --<-若是定义在上的增函数，且，求的范围（5）奇偶性、单调性的综合1．奇函数f(x)在[1,3]上为增函数，且有最小值7，则它在[-3,-1]上是____函数，有最___值___. 2．212()(11)()125ax b f x f x +=-=+函数是，上的奇函数，且． （1）确定()f x 的解析式；（2）用定义法证明()f x 在(1,1)-上递增；（3）解不等式(1)()0f t f t -+>．3．f(x)是定义在( 0，＋∞)上的增函数，且()()()xf f x f y y=-（1）求f (1)的值．（2）若f (6)= 1，解不等式 f ( x ＋3 )－f (x1) ＜2 ．5．函数的奇偶性（1）根据图像判断函数的奇偶性奇函数：关于原点对称；偶函数：关于y 轴对称 例：判断下列函数的奇偶性① y=x ³ ② y=|x|（2）根据定义判断函数的奇偶性一看定义域是否关于原点对称；二看()f x -与()f x 的关系1．设函数)(x f 和)(x g 分别是R 上的偶函数和奇函数，则下列结论恒成立的是（ ） A ．)()(x g x f +是偶函数 B ．)()(x g x f -是奇函数 C ．)()(x g x f +是偶函数 D ．)()(x g x f -是奇函数 2．已知函数()log (1)log (1)(01)a a f x x x a a =+-->≠且 （1）求()f x 的定义域；（2）判断()f x 的奇偶性并予以证明。

2015～2016学年度第一学期期末测试七 年 级 数 学本卷分值 100分，考试时间120分钟．一、选择题（本大题共10小题，每小题2分，共20分．在每小题给出的四个选项中，恰有一项是符合题目要求的，请将正确选项的字母代号填涂在答题卡相应位置．．．．．．．上） 1．34-的相反数是A ．43-B ．43C ．34-D ．342．单项式225x y-的系数和次数分别是A ．－2，2B ．2-，3C ．25-，2D ．25-，33．在下面的四幅图案中，通过平移图案（1）得到的是图案4．下列各组中的两项，不是．．同类项的是 A ．22x y 与23x y - B ．3x 与3xC ．232ab c -与32c b aD ．1与－18 5．若关于x 的方程710x a +-=解是1x =-，则a 的值等于A ．8B ．－8C ．6D ．－6 6．从三个不同方向看一个几何体，得到的三视图 如图所示，则这个几何体是A ．圆锥B ．圆柱C ．棱锥D ．球7．已知有理数a ，b 在数轴上表示的点如图所示，则下列式子中不正确．．．的是 A ．ab＜0 B ．a －b ＞0 C ．a ＋b ＞0 D ．ab ＜0b 0a（1） A B C D（第6题）（第7题）8． 如图，直线a ，b 被直线c 所截，则下列说法中错误．．的是 A ．∠1与∠2是邻补角 B ．∠1与∠3是对顶角C ．∠3与∠4是内错角D ．∠2与∠4是同位角 9． 如图，点D 在直线AE 上，量得∠CDE=∠A=∠C ，有以下三个结论：①AB ∥CD ；②AD ∥BC ；③∠B=∠CDA ．则正确的结论是A ．①②③B ．①②C ．①D ．②③ 10．王力骑自行车从A 地到B 地，陈平骑自行车从B 地到A 地，两人都沿同一公路匀速前进，已知两人在上午8时同时出发，到上午10时，两人还相距36 km ，到中午12时，两人又相距36 km ．求A 、B 两地间的路程．可设A 、B 两地间的路程为x km ，则下列所列方程中：①363624x x -+=；②36363622x -+=；③36362x -=⨯； ④3636x -=；其中正确的个数为A ．1个B ．2个C ．3个D ．4个二、填空题（本大题共10小题，每小题2分，共20分．不需写出解答过程，请把答案直接填写在答题卡相应位置．．．．．．．上） 11．用科学记数法表示9600000为 ▲ ．12．点A 、B 在同一条数轴上，其中点A 表示的数为－1，若点B 与点A 之间距离为3，则点B 表示的数为 ▲ ． 13．已知2a b -的值是2015，则124a b -+的值等于 ▲ ．14．若23(2)0x y -++=，则16xy = ▲ ．15．飞机的无风航速为a 千米／小时，风速为20千米／小时．则飞机逆风飞行4小时的行程是 ▲ 千米．16．某服装店以每件180元的价格卖出两件衣服，其中一件 盈利25%，另一件亏损25%，若盈利记为正，亏损记为负，则该店卖这两件衣服总的盈亏金额是 ▲ 元．17．如图，把小河里的水引到田地A 处就作AB ⊥l ，垂足 为B ，沿AB 挖水沟，这条水沟最短的理由是 ▲ ． 18. 如图，将三角板与两组对边分别平行的直尺贴在一起， 使三角板的顶点C （AC ⊥BC ）落在直尺的一边上，若∠1=24°，则∠2等于 ▲ 度． 19．如图，平面内有公共端点的6条射线OA 、OB 、OC 、 OD 、OE 、OF ，从射线OA 开始按逆时针方向依次在 射线上写上数字1、2、3、4、5、6、7…，则数字 “2016”应在射线 ▲ 上．20．已知线段AB =12㎝，若M 是AB 的三等分点，N 是AM 的中点，则线段BN 的长度为 ▲ ㎝．三、解答题（本大题共8小题，共60分．请在答题卡指定区域．．．．．．．内作答，解答时应写出文ac1 234 A B C DE（第8题） （第9题）（第17题）（第18题）（第19题）字说明、证明过程或演算步骤） 21．（每小题4分，共16分）计算：（1） (20)(3)(5)(7)-++---+；（2） 111()(12)462+-⨯-；（3） 322(2)(3)(4)2(3)(2)⎡⎤-+-⨯-+--÷-⎣⎦；（4） 471127326631440-+⨯-⨯÷．22．（每小题3分，共6分）（1）如图，点D 是线段AB 的中点，C 是线段AD 的中点，若AB ＝4㎝，求线段CD的长度．（2）如图，货船A 在灯塔O 的北偏东53°35′的方向上，客船B 在灯塔O 的南偏东28°12′的方向上．求∠AOB 的度数．23．（每小题4分，共8分）先化简，再求值：（1）求22113333a abc c a c +--+的值，其中1,2,36abc =-==-；（2）求2211312()()2323x x y x y --+-+的值，其中22,3x y =-=．24．（每小题4分，共8分）解方程： （1）72(33)20x x +-=； （2）121224x x+--=+．25．（本小题6分）如图，AD ∥BC ，∠1=60°，∠B =∠C ，DF 为∠ADC 的平分线． （1）求∠ADC 的度数；（2）试说明DF ∥AB ． 解：（1）根据题意完成填空（括号内填写理由）： ∵AD ∥BC （已知）∴∠B =∠1（ ） 又∵∠B =∠C （已知） ∴ =∠1=60°C D （第22题（2）） A O B 西 东 北南 （第22题（1））又∵AD ∥BC （已知）∴∠ADC +∠C =180°（ ） ∴∠ADC = ．（2）请你完成第2题的解答过程：26．（本小题4分）列方程解应用题：某车间有22名工人，每人每天可以生产1200个螺钉或2000个螺母．1个螺钉需要配2个螺母，为使每天生产的螺钉和螺母刚好配套，应安排生产螺钉和螺母的工人各多少名？ 27．（本小题6分）如图：已知AB ∥CD ，∠ABE 与∠CDE 两个角的角平分线相交于点F ． （1）如图1，若∠E ＝78°，则∠BFD = °；（2）如图2，若∠ABM ＝14∠ABF ，∠CDM ＝14∠CDF ，则∠M 和∠E 之间的数量关系为 ；（3）如图2，∠ABM ＝1n ∠MBF ，∠CDM ＝1n∠MDF ，设∠M ＝m °，直接用含有n ，m 的代数式表示出∠E ＝ °．28．（本小题6分）如图，在∠AOB 的内部作射线OC ，使∠AOC 与∠AOB 互补．将射线OA ，OC 同时绕点O 分别以每秒12°，每秒8°的速度按逆时针方向旋转，旋转后的射线OA ，OC 分别记为OM ，ON ，设旋转时间为t 秒．已知t ＜30，∠AOB ＝114°． （1）求∠AOC 的度数；（2）在旋转的过程中，当射线OM ，ON 重合时，求 t 的值； （3）在旋转的过程中，当∠COM 与∠BON 互余时，求 t 的值．BE DFACBE DFA CM 图1图2CMNB（第27题）。

XXX2015-2016学年高一上学期期末考试数学试卷 Word版含答案XXX2015-2016学年度第一学期期末考试高一数学一、选择题：本大题共8小题，共40分。

1.设全集 $U=\{1,2,3,4,5,6\}$，集合 $M=\{1,4\}$，$N=\{1,3,5\}$，则 $N\cap (U-M)=()$A。

$\{1\}$ B。

$\{3,5\}$ C。

$\{1,3,4,5\}$ D。

$\{1,2,3,5,6\}$2.已知平面直角坐标系内的点 $A(1,1)$，$B(2,4)$，$C(-1,3)$，则 $AB-AC=()$A。

$22$ B。

$10$ C。

$8$ D。

$4$3.已知 $\sin\alpha+\cos\alpha=-\frac{1}{\sqrt{10}}$，$\alpha\in(-\frac{\pi}{2},\frac{\pi}{2})$，则 $\tan\alpha$ 的值是（）A。

$-\frac{3}{4}$ B。

$-\frac{4}{3}$ C。

$\frac{3}{4}$ D。

$\frac{4}{3}$4.已知函数 $f(x)=\sin(\omega x+\frac{\pi}{4})$（$x\inR,\omega>0$）的最小正周期为 $\pi$，为了得到函数$g(x)=\cos\omega x$ 的图象，只要将 $y=f(x)$ 的图象（）：A.向左平移 $\frac{\pi}{4}$ 个单位长度B.向右平移$\frac{\pi}{4}$ 个单位长度C.向左平移 $\frac{\pi}{2}$ 个单位长度D.向右平移$\frac{\pi}{2}$ 个单位长度5.已知 $a$ 与 $b$ 是非零向量且满足 $3a-b\perp a$，$4a-b\perp b$，则 $a$ 与 $b$ 的夹角是（）A。

$\frac{\pi}{4}$ B。

$\frac{\pi}{3}$ C。

2015-2016学年度高二年级期末教学质量检测理科数学试卷一、选择题:本大题共10小题,每小题5分，共50分，在每小题给出的四个选项中，只有一项是符合题目要求的。

1．“0x >”是0>”成立的A ．充分非必要条件B ．必要非充分条件C ．非充分非必要条件D ．充要条件 2．抛物线24y x =的焦点坐标是A ．(1,0)B ．(0,1)C ．1(,0)16 D ．1(0,)163．与圆8)3()3(22=-+-y x 相切，且在y x 、轴上截距相等的直线有A ．4条B ．3条C ．2条D ．1条 4．设l 是直线，,αβ是两个不同的平面，则下列结论正确的是A ．若l ∥α，l ∥β，则//αβB ．若//l α，l ⊥β，则α⊥βC ．若α⊥β，l ⊥α，则l ⊥βD ．若α⊥β, //l α，则l ⊥β 5．已知命题p ：∀x 1，x 2∈R ，(f (x 2)-f (x 1))(x 2-x 1)≥0，则⌝p 是A ．∃x 1，x 2∈R ，(f (x 2)-f (x 1))(x 2-x 1)≤0B ．∀x 1，x 2∈R ，(f (x 2)-f (x 1))(x 2-x 1)≤0C ．∃x 1，x 2∈R ，(f (x 2)-f (x 1))(x 2-x 1)<0D ．∀x 1，x 2∈R ，(f (x 2)-f (x 1))(x 2-x 1)<06．设(2,1,3)a x = ，(1,2,9)b y =-，若a 与b 为共线向量，则A ．1x =，1y =B ．12x =，12y =-C ．16x =，32y =-D ．16x =-，32y =7．已知椭圆2215x y m +=的离心率5e =，则m 的值为A ．3B ．3C D ．253或38．如图,在正方体1111ABCD A BC D -中，,,M N P 分别是111,,B B B C CD 的中点，则MN 与1D P 所成角的余弦值为A． BCD ．9．如图，G 是ABC ∆的重心，,,OA a OB b OC c ===，则OG =A ．122333a b c ++B ．221333a b c ++C ．222333a b c ++D ．111333a b c ++10.下列各数中，最小的数是A ．75B ．)6(210 C ．)2(111111 D ．)9(8511．已知双曲线22214x yb-=的右焦点与抛物线y 2=12x 的焦 点重合，则该双曲线的焦点到其渐近线的距离等于 A ． B C ．3 D ．512、在如图所示的算法流程图中，输出S 的值为 A 、 11 B 、12 C 、1 D 、15二、填空题:本大题共4小题,每小题5分，满分20分13．若直线x +a y+2=0和2x+3y+1=0互相垂直，则a = 14．若一个圆锥的侧面展开图是面积为π2的半圆面，则该圆锥的体积为 。

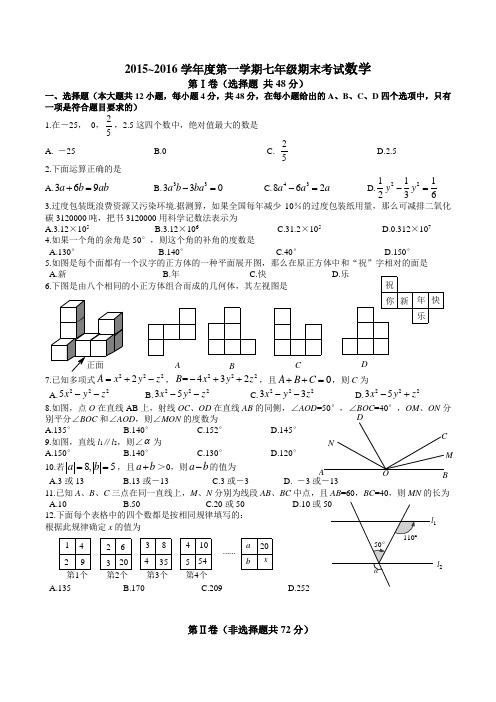
2015~2016学年度第一学期七年级期末考试数学第Ⅰ卷（选择题 共48分）一、选择题（本大题共12小题，每小题4分，共48分，在每小题给出的A 、B 、C 、D 四个选项中，只有一项是符合题目要求的）1.在－25， 0，25，2.5这四个数中，绝对值最大的数是 A. －25 B.0 C. 25D.2.5 2.下面运算正确的是 A.369a b ab += B.33330a b ba -= C.43862a a a -= D.22111236y y -= 3.过度包装既浪费资源又污染环境.据测算，如果全国每年减少10％的过度包装纸用量，那么可减排二氧化碳3120000吨，把书3120000用科学记数法表示为A.3.12×105B.3.12×106C.31.2×105D.0.312×1074.如果一个角的余角是50°，则这个角的补角的度数是A.130°B.140°C.40°D.150°5.如图是每个面都有一个汉字的正方体的一种平面展开图，那么在原正方体中和“祝”字相对的面是A.新B.年C.快D.乐6.下图是由八个相同的小正方体组合而成的几何体，其左视图是7.已知多项式2222A x y z =+-，222=432B x y z -++，且0A B C ++=，则C 为A.2225x y z --B.22235x y z --C.22233x y z --D.22235x y z -+8.如图，点O 在直线AB 上，射线OC 、OD 在直线AB 的同侧，∠AOD =50°，∠BOC =40°，OM 、ON 分别平分∠BOC 和∠AOD ，则∠MON 的度数为A.135°B.140°C.152°D.145° 9.如图，直线l 1∥l 2，则∠α为 A.150° B.140° C.130° D.120° 10.若8,5a b ==，且a b +＞0，则a b -的值为 A.3或13 B.13或－13 C.3或－3 D. －3或－1311.已知A 、B 、C 三点在同一直线上，M 、N 分别为线段AB 、BC 中点，且AB =60，BC =40，则MN 的长为A.10B.50C.20或50D.10或12.下面每个表格中的四个数都是按相同规律填写的： 根据此规律确定x 的值为A.135B.170C.209D.252第Ⅱ卷（非选择题共72分）乐快年新你祝D C B A NMD C B A l 2············第4个第3个第2个第1个35834∙∙∙···x 20b a 541054206329421二、填空题（本大题共4小题，每小题4分，共16分，请将最后答案填在题中横线上）13.312m a b 与212n a b -是同类项，则m n -=________； 14.规定符号＊运算为a ＊b =21ab a b -++，那么－3＊4=_____________；15.若代数式2245x x --的值为6，则2122x x --的值为_________； 16.为庆祝“六·一”儿童节，某幼儿园举行用火柴棒摆“金鱼”比赛，如图所示：按照上面的规律，摆第（n ）图，需用火柴棒的根数为_____________________.三、解答题（本大题共6个小题，共56分，解答时应写出必要的文字说明或演算步骤.）17.（本小题满分10分）计算与化简：（1）2241325(2)4-+----⨯-（）（） （2）224(6)3(2)x xy x xy +---18.（本小题满分8分）先化简，再求值：2211312()()2323a a b a b ----，其中22,3a b =-=.19.（本小题满分9分）一辆货车从货场A出发，向东走了2千米到达批发部B，继续向东走了1.5千米到达商场C，又向西走了4.5千米到达超市D，最后回到货场.（1）用一个单位长度表示1千米，以东为正方向，货场为原点，画出数轴并在数轴上标明货场A，批发部B，商场C，超市D的位置；（2）超市D距货场A多远？（3）货车一共行驶了多少千米？20.（本小题满分8分）某中学初一（四）班3位教师决定带领本班a名学生在五一期间取北京旅游，A旅行社的收费标准为：教师全价，学生半价；而B旅行社的收费标准为：不分教师、学生，一律八折优惠.（1）分别用代数式表示参加这两家旅行社所需的费用；（2）如果这3位教师要带领该班30名学生参加旅游，你认为选择哪一家旅行社较为合算，为什么？21.（本小题满分10分）如图，已知AB∥CE，∠A=∠E，试说明∠CGD=∠FHB.22.（本小题满分11分）HGFEDCBA将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起（其中，∠A=60°，∠D=30°，∠E=∠B=45°）.（1）1若∠DCE=45°，则∠ACB的度数为_________：2 若∠ACB=140°，则∠DCE的度数为______；（2）由（1）猜想∠ACB与∠DCE的数量关系，并说明理由；（3）当∠ACE＜180°且点E在直线AC的上方时，这两块三角尺是否存在一组边互相平行？若存在，请直接写出∠ACE所有可能的值（不必说明理由）；若不存在，请说明理由.。

一、主要存在的问题及其分析1、选择题和填空题得分率80%左右，选择题错得最多的是第11，12题，填空题错得最多的是第16题。

2、第17题，此题考察了平面向量的线性运算及数量积的坐标表示，涉及的知识面较全。

1、学生做题中较容易把向量平行的坐标表示与数量积的坐标表示混淆。

2、计算出现符号弄反的较多，估计是学生粗心所致。

3、第18题，本题有2个小题。

第（1）小题主要考查同角三角函数的基本关系，第（2）小题主要考查向量数量积，模的坐标表示及向量夹角余弦值，属于基础题型，基本上是公式的应用，但平均分不高，大概有6分。

存在问题主要是公式记不牢，计算不准确，对此，要加强对学生基本功，计算能力的提高。

4、第19题，本题主要考查学生对三角函数周期对称轴、对称中心、零点等方面知识的记忆与理解，属于中等偏易题型。

从学生的答题情况来看并不理想。

能拿满分12分的估计只有的学生，能拿到6分的也只有不到，甚至很多学生拿0分。

从学生答案分析，只要能对三角函数的周期、对称轴、对称中心熟练记忆与正确理解的都能拿到12分，但不少同学没有熟记或错误理解这些知识，从而没有答对。

例如对零点理解为坐标点，对称轴记为对称中心等。

另外还有部分同学因计算能力不好，在解方程时出现错误。

今后教学建议：（1）加强基础知识教学；（2）加强计算能力培养；（3）鼓励学生积极参与课堂教学积极应用所学的知识解题，答题。

5、第20题，考查目标：向量的坐标运算（加、减、数乘、数量积、求模均有考查）试题评价：该题目命题角度灵活，能很好体现向量法解决平面几何问题，在解决过程中几乎考查了“向量坐标运算”所有知识点。

能很好的考查学生对向量有关概念，定理的掌握。

难度：易主要存在问题：1、向量表示不规范，漏写“→”。

2、求对角线（求模）漏求另一条。

3、向量坐标求法（好多用起点减终点）4、第（2）问主要运算出错。

补救措施：1、加强基本概念、定理的讲解；2、加强基本题型的训练，让学生理解，巩固向量有关概念、定理等；3、加强答题书写的规范性；4、平时加强限时训练，提高计算的准确度、速度；6、第21题：本题主要考查函数的单调性、零点存在性定理和对数函数三个知识点，该题得分率偏低，大部分同学没能推理出最后的答案，平均得分7.1分，得分率为75.1%，主要存在的问题是推理问题，少部分学生是题目看不明。

2015-2016学年四川省成都七中高二（上）期末数学模拟试卷（理科）（一）一、选择题:本大题共12小题，每小题5分,共60分。

在每小题给出的四个选项中,只有一项是符合题目要求的.1．对某商店一个月内每天的顾客人数进行了统计，得到样本的茎叶图（如图所示），则该样本的中位数、众数、极差分别是（)A．46，45，56 B．46,45,53 C．47,45,56D．45，47，532．执行如图的框图，第3次和最后一次输出的A的值是（）A．7，9 B．5，11 C．7,11 D．5，93．对于线性回归方程，下列说法中不正确的是（）A．直线必经过点B．x增加一个单位时，y平均增加个单位C．样本数据中x=0时，可能有D．样本数据中x=0时,一定有4．如图,以等腰直角三角形斜边BC上的高AD为折痕，把△ABD和△ACD折成互相垂直的两个平面后,某学生得出下列四个结论:①；②∠BAC=60°;③三棱锥D﹣ABC是正三棱锥;④平面ADC的法向量和平面ABC的法向量互相垂直．其中正确的是（）A．①②B．②③C．③④D．①④5．若A、B两点的坐标分别是A（3cosa,3sina，1），B （2cosb，2sinb，1），则｜|的取值范围是( )A．B．C．（1，5） D．6．平面α与正四棱柱的四条侧棱AA1、BB1、CC1、DD1分别交于E、F、G、H．若AE=3，BF=4，CG=5，则DH等于( ）A．6 B．5 C．4 D．37．已知直线l的倾斜角为α,且60°＜α≤135°，则直线l斜率的取值范围是( ）A．B．C．D．8．已知：,求z=x2+y2最小值为（）A．13 B．C．1 D．9．已知圆C1：（x+1）2+(y﹣1）2=1，圆C2与圆C1关于直线x﹣y﹣1=0对称,则圆C2的方程为（）A．（x+2)2+（y﹣2）2=1 B．（x﹣2)2+（y+2)2=1C．（x+2）2+（y+2）2=1 D．(x﹣2）2+（y﹣2）2=110．已知圆x2+y2+2x﹣2y+a=0截直线x+y+2=0所得弦的长度为4，则实数a的值是( ）A．﹣2 B．﹣4 C．﹣6 D．﹣8 11．两个圆C1：x2+y2+2x+2y﹣2=0与C2:x2+y2﹣4x﹣2y+1=0的公切线有且仅有（)A．1条B．2条C．3条D．4条12．已知直线x+ay﹣1=0是圆C：x2+y2﹣4x﹣2y+1=0的对称轴，过点A（﹣4,a）作圆C的一条切线，切点为B,则|AB|=（)A．2 B．6 C．4D．2二、填空题:本大题共4小题，每小题4分，共16分。

广东省深圳市龙岗区2015-2016学年第一学期期末高二理科数学试题带答案龙岗区2015-2016学年第一学期期末质量监测试题高二（理科）数学本试卷共分为选择题和非选择题两部分，共22小题，满分150分，考试用时120分钟。

注意事项如下：1.答卷前，请检查答题卡是否整洁无缺损。

考生必须使用规定的笔将自己的学校、班级、姓名和考号填写在答题卡指定的位置上，并将监考教师发放的条形码正向准确粘贴在答题卡的贴条形码区。

请保持条形码整洁、不污损。

2.选择题请使用2B铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，请用橡皮擦干净后，再选涂其他答案。

不按以上要求作答的答案无效。

3.非选择题必须用黑色字迹钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上。

如需改动，请先划掉原来的答案，然后再写上新的答案。

不准使用铅笔和涂改液。

不按以上要求作答的答案无效。

4.请保持答题卡的整洁，不折叠、不破损。

考试结束后，请将试卷和答题卡一并交回。

第Ⅰ卷选择题（共60分）一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的。

1.已知命题p:x R，sinx1，则下列哪个命题是对p的否定？A．p:x R，sinx-1B．p:x R，sinx≥-1C．p:x R，sinx≤-1D．p:x R，sin(x2y2)+x≠12.1<k<4是方程4-kk-1的充分不必要条件。

A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分又不必要条件3.已知三角形ABC的三内角A，B，C成等差数列，且AB=1，BC=4，则该三角形面积为A．3B．2C．2/3D．4/34.在空间直角坐标系中，给定点M(2,-1,3)，若点A与点M关于xOy平面对称，点B与点M关于x轴对称，则AB=?A.2B.4C.25D.375.当a<-1时，不等式(x-a)/(x+1)(x-3)≤0的解集是A.(-∞,-1)∪[a,3]B.(-∞,a)∪[-1,3]C.(-∞,a)∪(-1,3)D.(-∞,a]∪(-1,3)6.若椭圆(a>b>0)的方程为x^2/a^2+y^2/b^2=1，离心率为e，则双曲线x^2/a^2-y^2/b^2=1的离心率为？A.2√5/5B.√3/2C.√5/2D.√3/5以下省略）7.已知等比数列{a_n}中，a_3=7，前3项之和S_3=21，则公比q的值为1或-1.8.若不等式组{x+3y≥4，XXX表示平面区域被直线y=kx分为面积相等的两部分，则k的值是3/4.9.如图所示的5×5正方形表格中共有20个空格，若在每一个空格中填入一个正整数，使得每一行和每一列都成等差数列，则字母a所代表的正整数是18.10.不等式f(x)=ax^2-x-c>0的解集为{x|-2<x<1}，则函数y=f(-x)的图象大致是关于y轴对称的。

2015～2016学年度第一学期期末考试试卷 高二（理） 数学 座位号第I 卷（选择题 共60分）一、选择题（本大题共12小题，每小题5分，共60分）1、向量(1,2,2),(2,4,4)a b =-=--，则a b 与 （ ） A 、相交 B 、垂直 C 、平行 D 、以上都不对2、如果双曲线的半实轴长为2，焦距为6，那么该双曲线的离心率是 （ ）A 、32B 、62C 、32D 、23、已知命题:,sin 1,p x R x ∀∈≤则p ⌝是 （ ） A 、,sin 1x R x ∃∈≥ B 、,sin 1x R x ∀∈≥ C 、,sin 1x R x ∃∈> D 、,sin 1x R x ∀∈>4、若向量)0,2,1(=a ，)1,0,2(-=b ，则（ ）A 0120,cos >=<b aB b a ⊥C b a //D ||||b a =5、若原命题“0,0,0a b ab >>>若则”，则其逆命题、否命题、逆否命题中（ ） A 、都真 B 、都假 C 、否命题真 D 、逆否命题真6、 “2320x x -+≠”是“1x ≠” 的（ ）条件 （ ） A 、充分不必要 B 、必要不充分 C 、充要 D 、既不充分也不必要 7、若方程x 225－m ＋y 2m ＋9＝1表示焦点在y 轴上的椭圆，则实数m 的取值范围是( )A 、－9＜m ＜25B 、8＜m ＜25C 、16＜m ＜25D 、m ＞88、已知△ABC 的周长为20，且顶点B (0，－4)，C (0，4)，则顶点A 的轨迹方程是（ ）A ．1203622=+y x （x ≠0）B ．1362022=+y x （x ≠0）C ．120622=+y x （x ≠0）D ．162022=+y x （x ≠0）9、一位运动员投掷铅球的成绩是14m ，当铅球运行的水平距离是6m 时，达到最大高度4m .若铅球运行的路线是抛物线，则铅球出手时距地面的高度是（ ） A ． 1.75m B ． 1.85mC ． 2.15mD ． 2.25m 10、设a R ∈，则1a >是11a< 的（ ） A ．充分但不必要条件 B ．必要但不充分条件C ．充要条件D ．既不充分也不必要条件 11.抛物线281x y -=的准线方程是 ( ) A ． 321=x B ． 2=y C ． 321=y D ． 2-=y12. 若A )1,2,1(-，B )3,2,4(，C )4,1,6(-，则△ABC 的形状是（ ） A ．不等边锐角三角形 B ．直角三角形C ．钝角三角形D ．等边三角形第II 卷（非选择题共90分）二、填空题(本大题共4小题，每小题5分，共20分)13、经过点(1,3)A -，并且对称轴都在坐标轴上的等轴双曲线的方程为 。