届高三数学下学期第一次开学考试试题文

绝密★考试结束前2023学年第二学期浙江七彩阳光新高考研究联盟返校考高三数学学科试题考生须知：1.本试卷共4页，满分150分，考试时间120分钟.2.答题前，在答题卷指定区域填写班级､姓名､考场号､座位号及准考证号.3.所有答案必须写在答题卷上，写在试卷上无效.4.考试结束后，只需上交答题卷.一､单项选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.若,M N 是I 的非空子集，M N M ∪=，则（ ） A.M N ⊆ B.N M ⊆ C.I N M ⊆ D.I M N ⊆2.若()1i 1z −=（i 是复数单位），则z =（ ）D.23.6611x x x x ++−的展开式中含2x 项的系数为（ ）A.-30B.0C.15D.304.设,a b 为正实数，则“a b >”是“22log ab >”的（ ） A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件5.某校1000名学生参加数学期末考试，每名学生的成绩服从()2105,15X N ∼，成绩不低于120分为优秀，依此估计优秀的学生人数约为（ ） A.23 B.46 C.159 D.317附：若()2,N ξµσ∼，则()0.6827,(22)0.9545P P µσξµσµσξµσ−<<+=−<<+=. 6.已知,a b 是异面直线，P 是空间任意一点，存在过P 的平面（ ） A.与,a b 都相交 B.与,a b 都平行 C.与,a b 都垂直 D.与a 平行，与b 垂直7.已知抛物线C ：22(0)y px p =>的焦点为F ，过F 作不与x 轴垂直的直线l 交C 于,A B 两点，设OAB 的外心和重心的纵坐标分别为,m n （O 是坐标原点），则mn的值为（ ） A.1 B.34 C.12 D.388.已知数列{}n a 的前n 项和为()2*1221,1,2,N n n n n S a a a a a n n ++===+∈，则下列结论不正确的是（ ）A.1n n a a +是递增数列 B.{}221n n a a +−是递增数列 C.101023S < D.13n na a +< 二､多项选择题：本题共3小题，每小题6分，共18分.在每小题给出的四个选项中，有多项符合题目要求.全部选对的得6分，部分选对的得部分分，有选错的得0分.9.已知向量()()1,1,2,0a b ==−，则下列结论正确的是（ ）A.||||a b =B.a 与b 的夹角为3π4C.()a b a +⊥D.b 在a 上的投影向量是()1,1−−10.已知函数()π2sin (0)6f x x ωω=−>图象关于点π,04中心对称，则下列结论正确的是（ ） A.()f x 的最小正周期3π B.π12f=C.()f x 的图象关于直线πx =对称D.()f x 的图象向左平移π4个单位长度后关于y 轴对称 11.已知函数()(),f x g x 定义域为R ，且()()()()()()()()()(),f x g y f y g x f x y g x g y f x f y g x y −=−−=−，()00g ≠，则下列结论正确的是（ ） A.()f x 为奇函数 B.()g x 为偶函数C.若()()111f g +=，则()()1001001f g −=D.若()()111f g −=，则()()1001001f g += 三､填空题：本题共3小题，每小题5分，共15分.12.一个宿舍的6名同学被邀请参加一个晚会，如果其中甲和乙两位同学要么都去，要么都不去，则不同去法的种数为__________.（用数字作答）13.函数()()π2cos sin2R 4f x x x x=−+∈的值域为__________. 14.已知正四面体ABCD 的边长为1,P 是空间一点，若222253PA PB PC PD +++=，则PA 的最小值为__________.四､解答题：本题共5小题，共77分.解答应写出文字说明､证明过程或演算步骤.15.（13分）已知等差数列{}n a 的各项均为正数，15932,5a a a a =+=. （1）求数列{}n a 的通项公式；（2）若数列{}n b 满足()*1211,N n n n n b a b a b n ++==∈，求{}n b 的通项公式及其前n 项和n S . 16.（15分）如图，四棱锥P ABCD −中，平面PAC ⊥平面,ABCD PAC 为等边三角形，AD ∥BC ，,22,BC CD BC CD AD M ⊥==是棱PA 的中点.（1）证明：PB MC ⊥；（2）求平面PAB 与平面PCD 所成角的余弦值.17.（15分）许多小朋友热衷于“套娃娃”游戏.在一个套娃娃的摊位上，若规定小朋友套娃娃成功1次或套4次后游戏结束，每次套娃娃成功的概率为13，每次套娃娃费用是10元. （1）记随机变量X 为小朋友套娃娃的次数，求X 的分布列和数学期望；（2）假设每个娃娃价值18元，每天有30位小朋友到此摊位玩套娃娃游戏，求摊主每天利润的期望.18.（17分）如图，已知椭圆221:12x C y +=，双曲线222:1(0).2x C y x P −=>是1C 的右顶点，过P 作直线1l 分别交1C 和2C 于点,A C ，过P 作直线2l 分别交1C 和2C 于点,B D ，设12,l l 的斜率分别为12,k k .（1）若直线AB 过椭圆1C 的右焦点，求12k k ⋅的值；（2）若121k k ⋅=−，求四边形ABCD 面积的最小值. 19.（17分）设实数0a >，已知函数()()2ln xf x e ax a ax =−+. （1）当1a =时，求函数()y f x =在()()1,1f 处的切线方程； （2）若()0f x ≥在[)1,x ∞∈+上恒成立，求a 的取值范围.2023学年第二学期浙江七彩阳光新高考研究联盟返校考高三数学参考答案一､单项选择题：本题共8小题，每小题5分，共40分，在每小题给出的四个选项中，只有一项是符合题目要求的.题号 1 2 3 4 5 6 7 8 答案BBDACADC8.提示：由题意易得0n a >，由221n n n a a a n ++=+得21121112n n n n n n n n a a a a na a a a a a ++++++>≥，所以A 正确；且1121212n n n n n n a a a a a a a −−−−=⋅> ，所以91010122211023S >+++=−= ，故C 错误；由上面知{}n a 也是递增数列，所以2222122n n n n n a a an a a ++++<+=，即22222221112n n n n n n a a a a n a a ++++−>−+>−，所以B 正确；由上得211112111222n n n n n n n n n n n n n a a a a n n na a a a a a ++++−−++=+<+=+⋅，累加得()1223351112322222n n n a a n n a a +−−<+++++≥ ，用错位相减法可求得()352323123183122222992n n n n n −−−+++++=−≥⋅ ， 所以12383123992n n n a n a +−+=+−<⋅，故D 正确. 二､多项选择题：本题共3小题.每小题6分，共18分.在每小题给出的四个选项中，有多项符合题目要求，全部选对的得6分，部分选对的得部分分，有选错的得0分.题号 9 10 11 答案BCDBCABD11.提示：由()()()()()f x g y f y g x f x y −=−得()()()()()f y g x f x g y f y x −=−， 所以()()f y x f x y −=−−，故()f x 是奇函数，所以A 正确； 由()()()()()g x g y f x f y g x y −=−得()()()()()g y g x f y f x g y x −=−， 所以()()g y x g x y −=−，故()g x 是偶函数，所以B 正确；由题意得()()()()()()()()()()f x y g x y f x g y f y g x g x g y f x f y −−−=−−+()()()()f y g y f x g x =+⋅− ，令1y =得()()()()()()1111f x g x f g f x g x −−−=+−由()f x 是奇函数得()00f =，且()()()()220]0]0,00g f g g −=≠ ，解得()01g =当()()111f g +=时，()()()()100100001f g f g −=−=− ，所以C 错误. 由题意得()()()()()()()()()()f x y g x y f x g y f y g x g x g y f x f y −+−=−+−()()()()g y f y f x g x =−⋅+ ，令1y =得()()()()()()1111f x g x g f f x g x −+−=−+ 当()()111f g −=时，()()()()100100100(1)001f g f g +=−+=，所以D 正确. 三､填空题：本题共3小题，每小题5分，共15分.12.32； 13.3,32−；； 15.提示：设O 是正四面体ABCD 内切球的球心，由体积法可求正四面体ABCD，正四面体ABCD，则 22222222PA PB PC PD PA PB PC PD +++=+++2222()()()()PO OA PO OB PO OC PO OD =+++++++()22424PO PO OA OB OC OD OA =+++++22235404423PO PO +++=，即PO = 所以P 是正四面体ABCD 内切球上一点，故PA的最小值为OA PA −==.四､解答题：本题共5小题，共77分解答应写出文字说明､证明过程或演算步骤.15.【解析】（1）设{}n a 的公差为d ，由题意得，()1121252a d a d +=+，所以，3d = 故，{}n a 的通项公式为()1131n a a n d n =+−=−.（2）由21n n n n a b a b ++=得，123135n n n n a b n b a n ++−==+，所以()()11221112113103231n n n n n n n n n b b b a a b a b b b b a a a n n −−−+−−=⋅=⋅=+− ， 所以()()103231n b n n =+−.由()()101011323133132nb n n n n==− +−−+得1110115101111313232323232558nnS n n n n =−+−++−=−−= −+++ . 16.【解折】（1）在梯形ABCD 中，由AD ∥,,22BC BC CD BC CD AD ⊥==，得AB AC ⊥.又平面ABCD ⊥平面PAC ，平面ABCD ∩平面,PAC AC AB =⊂平面ABCD ， 所以AB ⊥平面PAC ，所以平面PAB ⊥平面PAC 又等边,PAC M 是棱PA 的中点，所以MC PA ⊥， 所以MC ⊥平面PAB ， 故PB MC ⊥.（2）方法一：取AC 中点O ，易知OP AC ⊥，所以OP ⊥平面ABCD ，建立如图空间直角坐标系O xyz −，设4BC =，则()C()(()0,,,0,,A P M D ，由（1）知平面PAB的一个法向量是0,CM =，又)(,0,DCCP == 设(),,n x y z =是平面PCD 的法向量，则000n DC n CP ⋅= ⇒ ⋅=+= ， 令1z =，可得()n =，所以cos ,n CM n CM CMn ⋅===故，平面PAB 与平面PCD.方法二：延长BA 和CD 交于E 点，连接PE ，则平面PAB ∩平面PCD PE =因为由（1）MC ⊥平面PAB 所以过M 作MF PE ⊥于F 点，连接FC ，又因为CM PE ⊥，PE CM ⊥所以PE ⊥面MCF ，所以PE CF ⊥则MFC ∠为平面PAB 与平面PCD 所成角的平面角.又因为设4BC =则4,1,PB MF MC===CF =cos MFC ∠=故平面PAB 与平面PCD. 17.【解析】（1）由题意知，随机变量X 的取值为1,2,3,4，则()()()()231212214281,2,3,433393327327P X P X P X P X ==×========×= ， 即X 的分布列为所以()124865123439272727E X =×+×+×+×=. （2）易知小朋友套娃娃未成功的概率为4216381 =.，则小朋友套娃娃成功的概率为166518181−=. 记摊主每天利润为Y 元，则Y 的期望为()()65656526003010183010188127819E Y E X =××−×=××−×=，故摊主每天利润的期望为26009元.18.【解析】（1）设()()1122,,,A x y B x y ，直线AB 方程为1x my =+，与椭圆方程联立，得 ()22121222212210,,,22m my my y y y y m m −−=+=−=++++ ()()()212122121224222,1122m x x m y y x x my my m m −++=++==++=++，所以12k k ⋅（2）设()()()()11223344,,,,,,,A x y B x y C x y D x y ，直线,AC BD 方程分别为12121x n y x n y n n =+=−，联立1x n y =+与2212x y +=得1y =2y =，联立1x n y =+与2212x y −=得3y =，同理4y =， 所以四边形ABCD面积为412S AC BD y =⋅=−−令2212t n n =+，易知221202,02n n <<<<，且121n n =−，则52,,2t S ∈，因为S 关于t 单调递增，所以min 64212825169S ×==−， 当S 取最小值1289时，122,1,1t n n ===−，经检验满足题意. 19.【解析】（1）当1a =时，()()12ln ,2xxf x e x x f x e x=−+−+′= ()()12,11f e f e =−=−′所以所求切线方程为()()()112y e x e =−−+−，即()11y e x =−−. （2）由()0f x ≥得，()ln xe ax ax a ax −≥−（*）令()()ln ,x ag x x a x g x x′−=−=，易知()g x 在()0,a 上单调递减，(),a ∞+上单调递增当(]0,a e ∈时，因为[)1,x ∞∈+，所以,x e e a ax a ≥≥≥， 所以不等式（*）等价于()()xg eg ax ≥，也等价于xe ax ≥，即xe a x≤，又()'210x x e x e x x − =≥，所以x e x 在[)1,x ∞∈+上单调递增，x e e x ≥， 故(]0,a e ∈满足题意.当(),a e ∞∈+时，由xe x 在[)1,∞+上单调递增知，x e ax =在[)1,∞+上有唯一实数解，设为0x ，且()()000001,,,ln x x e ax ax x ∞∈+==. 所以()00002ln 0xf x e ax a ax =−+=， 所以要使()0f x ≥在[)1,x ∞∈+上恒成立，则()00f x ′=，另一方面，()()020000001220x a x a a f x e a ax a x x x ′−=−+=−+=>，矛盾.故(),a e ∞∈+不满足题意， 综合得，a 的取值范围为0a e <≤.（2）解法二：先证明()10f ≥对任意0a >恒成立，设()()()12ln (0),ln 1g a f e a a a a g a a ==−+>′=−，当()0,a e ∈时，()()0,g a g a ′<在()0,e 上单调递减，(),a e ∞∈+时，()()0,g a g a ′>在(),e ∞+上单调递增，所以()()0g a g e ≥=，即()10f ≥对任意0a >恒成立. 又()2xa f x e a x =−+′，设()2xa h x e a x =−+，则()2x a h x e x=−′， 易知()h x ′单调递增，所以()()1h x h ′≥′. 当(]0,a e ∈时，()()10,0h e a h x =−≥′≥′，所以()h x 单调递增，()()()()10,f x h x h e a f x =≥=−≥′单调递增， 所以()()10f x f ≥≥，符合题意. 当(),a e ∞∈+时，同解法一.。

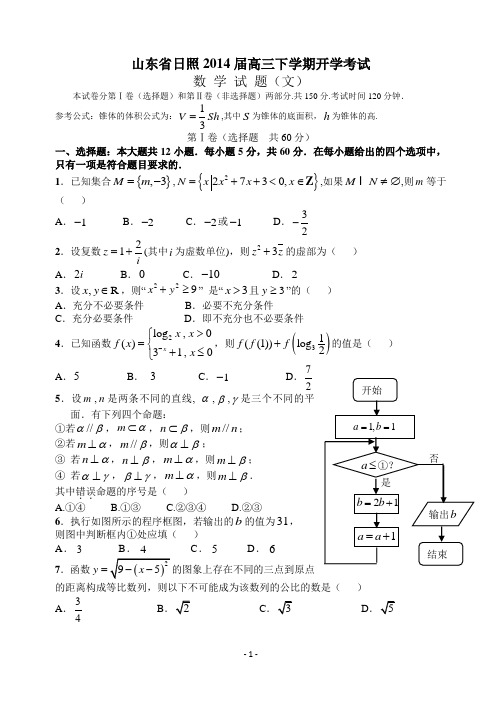
山东省日照2014届高三下学期开学考试数 学 试 题（文）本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分.共150分.考试时间120分钟． 参考公式：锥体的体积公式为：13VSh =,其中S 为锥体的底面积，h 为锥体的高. 第Ⅰ卷（选择题 共60分）一、选择题：本大题共12小题．每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知集合{},3M m =-,{}22730,N x x x x =++<∈Z ,如果M N ≠∅ ,则m 等于（ ）A ．1-B ．2-C ．2-或1-D ．32- 2．设复数21z i=+(其中i 为虚数单位)，则23z z +的虚部为（ ） A ．2i B ．0 C ．10- D ．23．设,R x y ∈，则“229x y +≥” 是“3x >且3y ≥”的（ ）A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．即不充分也不必要条件 4．已知函数2log ,0()31,0xx x f x x ->⎧=⎨+≤⎩，则()31((1))log 2f f f +的值是（ ）A ．5B ． 3C ．1-D ．725．设m ,n 是两条不同的直线, α,β,γ是三个不同的平面．有下列四个命题：①若//αβ，m α⊂，n β⊂，则//m n ； ②若m α⊥，//m β，则αβ⊥；③ 若n α⊥，n β⊥，m α⊥，则m β⊥； ④ 若αγ⊥，βγ⊥，m α⊥，则m β⊥． 其中错误．．命题的序号是（ ） A.①④ B.①③ C.②③④ D.②③6．执行如图所示的程序框图，若输出的b 的值为31， 则图中判断框内①处应填（ ）A ．3B ．4C ．5D ．67．函数y =的距离构成等比数列，则以下不可能成为该数列的公比的数是（ ） A ．34BCD甲 乙14628543974237228514158．以下正确命题的个数为（ ）①命题“存在R x ∈，220x x --≥”的否定是：“不存在R x ∈，220x x --<”；②函数131()()2x f x x =-的零点在区间11(,32内； ③ 函数()xx f x ee -=-的图象的切线的斜率的最大值是2-；④线性回归直线y bx a =+ 恒过样本中心(),x y ，且至少过一个样本点.A ．3B ．1C ．0D ．2 9．下图是某赛季甲、乙两名篮球运动员每场比赛 得分的茎叶图，则甲、乙两人这几场比赛得分的中位数之和是（ ）A ．68B ．70C ．69D ．71 10．已知函数1π()cos ,[,222f x x x x π=+∈-，01sin 2x =,0π[,]22x π∈-．那么下面命题中真命题的序号是（ ）①()f x 的最大值为0()f x ② ()f x 的最小值为0()f x ③()f x 在0[,]2x π-上是增函数 ④ ()f x 在0π[,2x 上是增函数 A ．①③ B ．①④ C ．②③D ．②④11．一个几何体的三视图如图所示，其中正视图是一个正三角形，则这个几何体的 （ ）A ．外接球的半径为3B1CD ．外接球的表面积为4π12．过双曲线)0,0(12222>>=-b a b y a x 的左焦点)0)(0,(>-c c F 作圆4222a y x =+的切线，切点为E ,延长FE 交双曲线右支于点P ，若2OF OP OE +=,则双曲线的离心率为（ ）A ．2B ．510C ．210D ．10第Ⅱ卷（非选择题 共90分）二、填空题：本大题共4小题，每小题4分，共16分．13．若tan 2,sin cos ==ααα则 .14．已知直线y x a =+与圆224x y +=交于A 、B 两点，且0OA OB ⋅=，其中O 为坐标原点，则正实数a 的值为.正视图侧视图俯视图AB1A 1B 1C 15．设等轴双曲线221y x -=的两条渐近线与直线2x =围成的三角形区域（包含边界）为M ，(,)P x y 为M 内的一个动点，则目标函数2z x y =-的最大值为 . 16．已知函数()f x 的定义域为[]15,-，部分对应值如下表, ()f x 的导函数()y f x '=的图象如图所示. 下列关于()f x 的命题： ①函数()f x 的极大值点为0，4； ②函数()f x 在[]02,上是减函数； ③如果当[]1x ,t ∈-时，()f x 的最大值是2，那么t 的最大值为4；④当12a <<时，函数()y f x a =-有4个零点； ⑤函数()y f x a =-的零点个数可能为0、1、2、3、4个．其中正确命题的序号是 ．三、解答题：本大题共6小题，共74分，解答时应写出必要的文字说明、证明过程或演 算步骤． 17．（本小题满分12分）已知向量)cos ,(sin ),sin 3,(sin x x x x -==，设函数x f ⋅=)(.（Ⅰ）求函数()f x 在3[0,]2π上的单调递增区间； （Ⅱ）在ABC ∆中，a ，b ，c 分别是角A ，B ，C 的对边，A 为锐角，若162sin()(=-+πA A f ，7=+c b ，ABC ∆的面积为32，求边a 的长．18．（本小题满分12分）一汽车厂生产A,B,C 三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如表所示(单位:辆)，若按A,B,C 三类用分层抽样的方法在这个月生产的轿车中抽取50辆,则A 类轿车有10辆.（Ⅰ）求z 的值；（Ⅱ）用随机抽样的方法从B 类舒适型轿车中抽取8辆,经检测它们的得分如下: 9.4, 8.6, 9.2, 9.6, 8.7, 9.3,9.0, 8.2. 把这8辆轿车的得分看作一个总体,从中任取一个分数a .记这8辆轿车的得分的平均数为x ，定义事件E ={0.5a x -≤，且函数()2 2.31f x ax ax =-+没有零点}，求事件E 发生的概率.19．（本小题满分12分）如图，在多面体111ABC A B C -中，四边形11ABB A 是正方形，1AC AB ==，11AC A B =，11//B C BC ，1112B C =BC . （Ⅰ）求证：面1A AC ⊥面ABC ； （Ⅱ）求证：1//AB 面11AC C .20．（本小题满分12分）已知集合{}21,N A x x n n *==--∈,{}63,N B x x n n *==-+∈，设n S 是等差数列{}n a 的前n 项和,若{}n a 的任一项B A a n ∈,且首项1a 是A B 中的最大数,10750300S -<<-.（Ⅰ）求数列{}n a 的通项公式;（Ⅱ）若数列{}n b 满足139(2n a n n b +-=， 求12233445212221n n n n a b b a a b b a a b b a -+-+-++- 的值.21．（本小题满分13分）设1F ,2F 分别是椭圆D ：)0(12222>>=+b a by a x 的左、右焦点，过2F 作倾斜角为3π的直线交椭圆D 于A ,B 两点, 1F 到直线AB 的距离为3,连结椭圆D 的四个顶点得到的菱形面积为4.（Ⅰ）求椭圆D 的方程； （Ⅱ）过椭圆D 的左顶点P 作直线1l 交椭圆D 于另一点Q , 若点),0(t N 是线段PQ 垂直平分线上的一点,且满足4=⋅,求实数t 的值．22．（本小题满分13分）已知函数()3213f x x ax bx =++()R a,b ∈. （Ⅰ）若曲线()C :y f x =经过点()12P ,，曲线C 在点P 处的切线与直线2140x y +-=垂直，求a,b 的值；（Ⅱ）在（Ⅰ）的条件下，试求函数()()()2713g x m f x x ⎡⎤=--⎢⎥⎣⎦（m 为实常数，1m ≠±）的极大值与极小值之差；（Ⅲ）若()f x 在区间()12,内存在两个不同的极值点，求证：02a b <+<.数学 (文科) 参考答案及评分标准一、选择题：本大题共12小题．每小题5分，共60分． C D B A A B D D C A B C二、填空题：本大题共4小题，每小题4分，共16分． 13.2514. 2 15. 6 16. ①②⑤ 三、解答题：本大题共6小题，共74分，解答时应写出必要的文字说明、证明过程或演 算步骤． 17．（本小题满分12分）解：（Ⅰ）由题意得21cos 2()sin cos 222x f x x x x x -==-1sin(2)26x π=-+ ………………………………………………………………………3分 令3222262k x k πππππ+≤+≤+,Z k ∈ 解得：263k x k ππππ+≤≤+，Z k ∈ 30,2x π⎡⎤∈⎢⎥⎣⎦，263x ππ∴≤≤，或7362x ππ≤≤所以函数()f x 在3[0,]2π上的单调递增区间为2[,]63ππ，73,62ππ⎡⎤⎢⎥⎣⎦…………………6分（Ⅱ）由1)62sin()(=-+πA A f 得：1)62sin()62sin(21=-++-ππA A化简得：212cos -=A又因为02A π<<，解得：3π=A …………………………………………………………9分由题意知：32sin 21==∆A bc S ABC，解得8=bc ， 又7=+c b ,所以22222cos ()2(1cos )a b c bc A b c bc A =+-=+-+14928(1)252=-⨯⨯+=故所求边a 的长为5. ……………………………………………………………………12分18. （本小题满分12分）解：(Ⅰ)设该厂本月生产轿车为n辆,由题意得:5010100300n =+,所以2000n =.z =2000-100-300-150-450-600=400 ………………………………4分(Ⅱ) 8辆轿车的得分的平均数为1(9.48.69.29.68.79.39.08.2)98x =+++++++=…………………………………………6分把8辆轿车的得分看作一个总体,从中任取一个分数a 对应的基本事件的总数为8个, 由0.5a x -≤，且函数()2 2.31f x ax ax =-+没有零点290.58.59.249.240a a a a ⎧-≤⇒⇒≤<⎨∆=-<⎩………………………………………………10分 ∴E 发生当且仅当a 的值为：8.6, 9.2, 8.7, 9.0共4个,()4182p E ∴== ……………………………………………………………………12分19．（本小题满分12分） 证明：（Ⅰ） 四边形11ABB A 为正方形, ∴11A A AB AC ===, 1A A AB ⊥∴1A B = …………………………………2分11AC A B =∴1AC = ∴190A AC O ∠= ∴1A A AC ⊥ ………………………………4分 AB AC A = ，∴1A A ⊥面ABC 又 1A A ⊂面1A AC ，∴面1A AC ⊥面ABC ………………………………6分 （Ⅱ）取BC 的中点E ，连结AE ，1C E ，1B E11B C //BC ，11B C =12BC ，1111//,B C EC B C EC ∴= ∴四边形11CEB C 为平行四边形 ∴1B E //1C C 1C C ⊂面11AC C ，1B E ⊄面11AC C ∴1B E //面11AC C ……………………8分11//B C BC ，11B C =12BC ， 1111//,B C BE B C BE ∴=∴四边形11BB C E 为平行四边形∴11//B B C E ，且1B B =1C E 又 11ABB A 是正方形，∴11//A A C E ，且1A A =1C E ∴11AEC A 为平行四边形，∴11//AE AC , 11AC ⊂面11AC C ，AE ⊄面11AC C ∴//AE 面11AC C ………………………………………………………………………10分 1AE B E E = ，∴面1//B AE 面11AC C 1AB ⊂面1B AE ，∴1//AB 面11AC C ………………………………………………12分20．（本小题满分12分）解: （Ⅰ）由题设知: 集合A 中所有元素可以组成以3-为首项,2-为公差的递减等差数列；集合B 中所有的元素可以组成以3-为首项,6-为公差的递减等差数列. 由此可得,对任意的N n *∈,有B B A =A B 中的最大数为3-,即13a =- …………………………………………………3分1A 1B 1C A BCE设等差数列{}n a 的公差为d ,则3(1)n a n d =-+-,1101010()45302a a S d +==-因为10750300S -<<-, ∴7504530300d -<-<-,即616-<<-d 由于B 中所有的元素可以组成以3-为首项,6-为公差的递减等差数列,所以)0,(6≠∈-=m Z m m d ,由1666m -<-<-2m ⇒=，所以12-=d所以数列{}n a 的通项公式为912n a n =-（*∈N n ） …………………………………8分（Ⅱ）139n a n n nb +-==…………………………………………………………9分 于是有12233445212221n n n n a b b a a b b a a b b a -+-+-++-21343565722121()()()()n n n b a a b a a b a a b a a -+=-+-+-++-21．（本小题满分13分）解：（Ⅰ）设1F ,2F 的坐标分别为)0,(),0,(c c -,其中0>c由题意得AB 的方程为:)(3c x y -= 因1F 到直线AB 的距离为3,所以有31333=+--cc ,解得3=c …………………1分所以有3222==-c b a……………………①由题意知: 42221=⨯⨯b a ,即2=ab ……②联立①②解得:1,2==b a所求椭圆D 的方程为1422=+y x …………………………………………5分 （Ⅱ）由（Ⅰ）知:)0,2(-P , 设),(11y x Q根据题意可知直线1l 的斜率存在，可设直线斜率为k ,则直线1l 的方程为)2(+=x k y把它代入椭圆D 的方程,消去y ,整理得: 0)416(16)41(2222=-+++k x k x k由韦达定理得22141162k k x +-=+-,则2214182k k x +-=,=+=)2(11x k y 2414k k +，222284,1414k k Q k k ⎛⎫-∴ ⎪++⎝⎭，线段PQ 的中点坐标为,418(22k k +-)4122k k +………………7分 (ⅰ)当0=k 时, 则有)0,2(Q ,线段PQ 垂直平分线为y 轴于是),2(),,2(t t -=--=由442=+-=⋅t ,解得:22±=t ……………………………………………9分因为点),0(t N 是线段PQ 垂直平分线的一点,令0=x,得:2416k kt +-=，于是),(),,2(11t y x NQ t NP -=--=由4)41()11516(4)(2222411=+-+=---=⋅k k k t y t x ,解得:714±=k代入2416kk t +-=,解得:5142±=t 综上, 满足条件的实数t 的值为22±=t 或5142±=t ……………………………13分246211[1()]12224()2424(1)1212n n nb b b b -=++++=⨯=-- …………………………12分22.（本小题满分13分） 解：（Ⅰ）⇒()22f x x ax b '=++，直线2140x y +-=的斜率为12-，∴曲线C 在点P 处的切线的斜率为2, ()1122f a b '∴=++=……①曲线()C :y f x =经过点()12P ,，()1123f a b ∴=++=……②由①②得：2,37.3a b ⎧=-⎪⎪⎨⎪=⎪⎩……………………………………………………………………3分 （Ⅱ）由（Ⅰ）知：()32127333f x x x x =-+，∴()()232123m g x x x -=-，()()2413g x m x x ⎛⎫'∴=-- ⎪⎝⎭, 由()00g x x '=⇒=，或43x =.当210m ->，即1m ,>或1m <-时，x ，()g x '，()g x 变化如下表()()()403g x g x g g ⎛⎫-=- ⎪⎝⎭极大极小()()2232320118181m m ⎡⎤=---=-⎢⎥⎣⎦ ……………5分当210m ,-<即11m -<<时，x ，()g x '，()g x 变化如下表()()()403g x g x g g ⎛⎫-=- ⎪⎝⎭极大极小()()2232321018181m m =---=--………………7分综上可知：当1m ,>或1m <-时，()()g x g x -=极大极小()232181m -；当11m -<<时，()()g x g x -=极大极小()232181m --……………………………………8分 （Ⅲ）因为()f x 在区间()12,内存在两个极值点 ，所以()0f x '=，即220x ax b ++=在(1,2)内有两个不等的实根． ∴2(1)120,(1)(2)440,(2)12,(3)4()0.(4)f a b f a b a a b '=++>⎧⎪'=++>⎪⎨<-<⎪⎪∆=->⎩ …………………………………………………………10分 由 （1）+（3）得：0a b +>，………………………………………………………11分由（4）得：2a b a a +<+，由（3）得：21a -<<-，∴2211()224a a a +=+-<，∴2ab +<．故02a b <+< …………………………………………………………………………13分。

2024届奉贤中学高三（下）数学开学一､填空题（第1-6题每题4分，第7-12题每题5分，满分54分）1.函数2()1f x x =-的定义域是________.2.函数y =2x+6从x =2到x =2.5的平均变化率是_________.3.若一个圆锥的母线长是底面半径的3倍，则该圆锥的侧面积是底面积的_________倍；4.已知两个单位向量a ，b满足4a b +=，则向量a ，b 的夹角为______．5.已知虚数1+2i 是方程20()x ax b a b R ++=∈、的一个根，则a b +=____6.下列命题中错误的是__．①将一组数据中的每个数都加上或减去同一个常数后，均值与方差都不变；②在一组样本数据()()()1122,,,,,,n n x y x y x y （122,,,,nn x x x ≥L不全相等）的散点图中，若所有样本点(),(1,2,,)i i x y i n = 都在直线112y x =-+上，则这组样本数据的线性相关系数为12-；③在吸烟与患肺病这两个分类变量的计算中，若由独立性检验知，在犯错误率不超过0.01的前提下，认为吸烟与患肺病有关系．若某人吸烟，则他有99%的可能性患肺病．7.从1，2，3，…，15中，甲，乙两人各任取一数（不重复），已知甲取到的是5的倍数，则甲数大于乙数的概率是_______．8.在10202311x x ⎛⎫++ ⎪⎝⎭的展开式中，2x 项的系数为__________.（结果用数值表示）9.图1为一种卫星接收天线，其曲面与轴截面的交线为抛物线的一部分，已知该卫星接收天线的口径6AB =，深度2MO =，信号处理中心F 位于焦点处，以顶点O 为坐标原点，建立如图2所示的平面直角坐标系xOy ，若P 是该抛物线上一点，点15,28Q ⎛⎫⎪⎝⎭，则PF PQ+的最小值为__________．10.已知定义在R 上的偶函数()f x 满足()()114f x f x ++-=.若()00f =，且()f x 在[]0,1单调递增，则满足π()sin24xf x ⋅≥的x 的取值范围是__________.11.若函数()sin cos 1sin cos f x a x b x b x a x=+-+-(,R a b ∈)的最大值为11，则22a b +=___________.12.已知n S 为数列{}n a 的前n 项和，数列{}n a 满足12a =-，且32n n S a n =+，()f x 是定义在R 上的奇函数，且满足()()2=f x f x -，则()2021f a =______．二､单选题（本大题共4题，满分20分）13.已知实数a 、b ，那么||||||a b a b +=-是0ab <的（）条件．A.充分不必要B.必要不充分C.充要D.既不充分也不必要14.设两个正态分布2111()(0)N μσσ>，和2222()(0)N μσσ>，的密度函数图像如图所示．则有A .1212,μμσσ<<B.1212,μμσσ<>C.1212,μμσσ><D.1212,μμσσ>>15.在圆锥PO 中，已知高2PO =，底面圆的半径为4，M 为母线PB 的中点，根据圆锥曲线的定义，下列四个图中的截面边界曲线分别为圆、椭圆、双曲线及抛物线，下面四个命题，正确的个数为（）①圆的面积为4π；；③双曲线两渐近线的夹角正切值为34；④抛物线的焦点到准线的距离为455A.1个B.2个C.3个D.4个16.如图，正四棱锥P ABCD -的底面边长和高均为2，M 是侧棱PC 的中点，若过AM 作该正四棱锥的截面，分别交棱PB ､PD 于点E ､F (可与端点重合)，则四棱锥P AEMF -的体积的取值范围是（）A.1,12⎡⎤⎢⎥⎣⎦B.14,23⎡⎤⎢⎥⎣⎦C.41,3⎡⎤⎢⎣⎦D.8,19⎡⎤⎢⎥⎣⎦三､解答题（本大题共有5题，满分76分）17.在三棱锥A BCD -中，2AB AD BD ===，BC DC ==，2AC =.（1）求证：BD AC ⊥；（2）若P 为AC 上一点，且34AP AC =，求直线BP 与平面ACD 所成角的正弦值.18.在△ABC 中，a ，b ，c 分别是内角A ，B ，C 的对边，()2,m a c b =+ ，()cos ,cos n B C =，0m n ⋅=.（1）求角B 大小；（2）设()()2π2cos sin 2sin sin 2sin cos cos 3f x x x x B x x A C ⎛⎫=+-++ ⎪⎝⎭，当2,63ππx ⎡⎤∈⎢⎥⎣⎦时，求()f x 的最小值及相应的x .19.一项试验旨在研究臭氧效应.实验方案如下：选40只小白鼠，随机地将其中20只分配到实验组，另外20只分配到对照组，实验组的小白鼠饲养在高浓度臭氧环境，对照组的小白鼠饲养在正常环境，一段时间后统计每只小白鼠体重的增加量（单位：g ）.（1）设X 表示指定的两只小白鼠中分配到对照组的只数，求X 的分布列和数学期望；（2）实验结果如下：对照组的小白鼠体重的增加量从小到大排序为：15.218.820.221.322.523.225.826.527.530.132.634.334.835.635.635.836.237.340.543.2实验组的小白鼠体重的增加量从小到大排序为：7.89.211.412.413.215.516.518.018.819.219.820.221.622.823.623.925.128.232.336.5（i ）求40只小鼠体重的增加量的中位数m ，再分别统计两样本中小于m 与不小于的数据的个数，完成如下列联表：m<m≥对照组实验组（ii ）根据（i ）中的列联表，能否有95%的把握认为小白鼠在高浓度臭氧环境中与正常环境中体重的增加量有差异．附：()()()()22(),n ad bc K a b c d a c b d -=++++0k 0.1000.0500.010()20P K k ≥ 2.7063.8416.63520.已知点12F F 、为双曲线()222210,0x y a b a b-=>>的左右焦点，过2F 作垂直于x 轴的直线，在x 轴上方交双曲线于点M ，且121230,MF F MF F ∠=︒△的面积为.圆O 的方程是222x y r +=.（1）求双曲线的方程；（2）过双曲线上任意一点P 作该双曲线两条渐近线的垂线，垂足分别为12P P 、，求12PP PP ⋅的值；（3）过圆O 上任意一点Q 作圆O 的切线l 交双曲线C 于A B 、两点，AB 中点为N ，若||2||AB ON =恒成立，试确定圆O 半径r .21.已知()f x 是定义在[],a b 上的函数，如果存在常数0M >，对区间[],a b 的任意划分：011n n a x x x x b -=<<<<=L ，和式()()11ni i i f x f x M -=-≤∑恒成立，则称()f x 为[],a b 上的“绝对差有界函数”，注：121nin i aa a a ==+++∑ .（1）求证：函数()sin cos f x x x =+在,02p轾-犏犏臌上是“绝对差有界函数”；（2）记集合(){|A f x =存在常数0k >，对任意的[]12,,x x a b ∈，有()()1212f x f x k x x -≤-成立.求证：集合A 中的任意函数()f x 为“绝对差有界函数”；（3）求证：函数()cos,01{20,0x x f x xx π<≤==不是[]0,1上的“绝对差有界函数”.2024届奉贤中学高三（下）数学开学一､填空题（第1-6题每题4分，第7-12题每题5分，满分54分）1.函数()1f x x =-的定义域是________.【答案】{|2x x - 且1}x ≠【解析】【分析】根据分明不为零以及偶次根式下被开方数非负列不等式求解.【详解】由题意，要使函数有意义，则1020x x -≠⎧⎨+≥⎩，解得，1x ≠且2x ≥-；故函数的定义域为：{|2x x - 且1}x ≠.故答案为：{|2x x - 且1}x ≠.【点睛】本题考查函数定义域，考查基本分析求解能力，属基础题.2.函数y =2x+6从x =2到x =2.5的平均变化率是_________.【答案】2【解析】【分析】计算自变量的增量 2.52x ∆=-与函数值的增量(2.5)(2)y f f ∆=-，可得平均变化率y x∆∆.【详解】函数y=2x+6从x=2到x=2.5的平均变化率是()2 2.56226ΔΔ 2.52y x ⨯+-⨯+=-=2.故答案为2.【点睛】本题考查平均变化率的概念、计算，属于简单题.3.若一个圆锥的母线长是底面半径的3倍，则该圆锥的侧面积是底面积的_________倍；【答案】3；【解析】【分析】分别计算侧面积和底面积后再比较．【详解】由题意3l r =，23S rl r ππ==侧，2S r π=底，∴3S S 侧底＝．故答案为3．【点睛】本题考查圆锥的侧面积，掌握侧面积计算公式是解题关键．属于基础题．4.已知两个单位向量a ，b 满足4a b += ，则向量a ，b 的夹角为______．【答案】23π##120 【解析】【分析】首先根据平面向量的运算律求出a b ⋅，再根据夹角公式计算可得；【详解】解：由单位向量a ，b满足4a b += 2413a b += ，所以2216813a a b b +⋅+= ，12a b ⋅=- ，所以1cos ,2a b a b a b ⋅==-⋅，又[],0,π∈ a b ,所以2,3a b π= .故答案为：23π5.已知虚数1+2i 是方程20()x ax b a b R ++=∈、的一个根，则a b +=____【答案】3【解析】【分析】根据实系数的一元二次方程20x ax b ++=的两个虚数根互为共轭复数，再利用根与系数的关系，即可求出a 、b 的值．【详解】虚数12i +是方程20x ax b ++=的一个根，∴共轭虚数12i -也是此方程的一个根，12()(1212)2a x x i i ∴=-+=-++-=-；12(12)(12)5b x x i i ==+-=；253a b ∴+=-+=．故答案为：3．【点睛】本题考查了实系数的一元二次方程两个虚数根互为共轭复数以及根与系数关系的应用问题，是基础题．6.下列命题中错误的是__．①将一组数据中的每个数都加上或减去同一个常数后，均值与方差都不变；②在一组样本数据()()()1122,,,,,,n n x y x y x y （122,,,,n n x x x ≥L 不全相等）的散点图中，若所有样本点(),(1,2,,)i i x y i n = 都在直线112y x =-+上，则这组样本数据的线性相关系数为12-；③在吸烟与患肺病这两个分类变量的计算中，若由独立性检验知，在犯错误率不超过0.01的前提下，认为吸烟与患肺病有关系．若某人吸烟，则他有99%的可能性患肺病．【答案】①②③【解析】【分析】根据均值和方差的性质，相关系数的特点，独立性检验的相关知识，对每个选项进行逐一分析，即可判断和选择.【详解】对于①，将一组数据中的每个数都加上或减去同一个常数后，均值改变，方差不变，所以①错误；对于②，在散点图中，若所有样本点都在直线112y x=-+上，则这组样本数据的线性相关系数为1-，所以②错误；对于③，由独立性检验得，有99%的把握认为吸烟与患肺病有关系时，是指有1%的可能性使推断出现错误，所以③错误．综上，错误的命题序号是①②③．故答案为：①②③.7.从1，2，3，…，15中，甲，乙两人各任取一数（不重复），已知甲取到的是5的倍数，则甲数大于乙数的概率是_______．【答案】9 14【解析】【分析】先求出基本事件总数，再求出甲数a大于乙数b包含的基本事件(),a b个数，再由古典概型的概率公式求解.【详解】从1，2，3，…，15中，甲、乙两人各取一数(不重复)，甲取到的数是5的倍数，则基本事件总数31442n=⨯=，则甲数a大于乙数b包含的基本事件(),a b有：()(5,1),(5,2),(5,3),(5,4),(10,1),(10,2),10,3，(10,4),(10,5),(10,6),(10,7),(10,8),(10,9),(15,1)，(15,2),(15,3),(15,4),(15,(15,5),(7),(15,6),15,8)，()(15,9),(15,10),(15,11),(15,12),(15,13),15,14，共27个，∴甲数大于乙数的概率2794214 P==．故答案为：9 148.在10202311xx⎛⎫++⎪⎝⎭的展开式中，2x项的系数为__________.（结果用数值表示）【答案】45【解析】【分析】由二项式展开得2x 项只能在10(1)x +展开式中，进一步结合二项式系数即可求解.【详解】()101010191020232023202311111(1)C (1)x x x x x x x ⎛⎫⎛⎫++=++=++++ ⎪ ⎪⎝⎭⎝⎭ ，2x ∴项只能在10(1)x +展开式中，即为8210C x ，系数为810120109452C C 1⨯===⨯.故选：45.9.图1为一种卫星接收天线，其曲面与轴截面的交线为抛物线的一部分，已知该卫星接收天线的口径6AB =，深度2MO =，信号处理中心F 位于焦点处，以顶点O 为坐标原点，建立如图2所示的平面直角坐标系xOy ，若P 是该抛物线上一点，点15,28Q ⎛⎫⎪⎝⎭，则PF PQ +的最小值为__________．【答案】3【解析】【分析】由题意可知点()2,3在抛物线上，利用待定系数法求抛物线方程，结合抛物线定义求PF PQ +的最小值.【详解】设抛物线的方程为()220y px p =>，因为6AB =，2MO =，所以点()2,3A 在抛物线上，所以94p =，故94p =，所以抛物线的方程为292y x =，所以抛物线的焦点F 9,08⎛⎫⎪⎝⎭，准线方程为98x =-，在方程292y x =中取158x =可得2135416y =>，所以点Q 在抛物线内，过点P 作PP '与准线垂直，P '为垂足，点Q 作QQ '与准线垂直，Q '为垂足，则PF PP '=，所以159388PF PQ PP PQ QQ ''+=+≥=+=，当且仅当直线PQ 与准线垂直时等号成立，所以PF PQ +的最小值为3.故答案为：3.10.已知定义在R 上的偶函数()f x 满足()()114f x f x ++-=.若()00f =，且()f x 在[]0,1单调递增，则满足π()sin 4x f x ⋅≥的x 的取值范围是__________.【答案】[]18,38,Z k k k ++∈【解析】【分析】由题意可知，()f x 是周期为4的周期函数，πsin4y x =的最小正周期为8，结合()f x 与πsin 4y x =的单调性，易知在一个周期内，由π()sin 4xf x ⋅≥，可得[]1,3x ∈，再结合周期求出范围即可.【详解】因为()f x 是偶函数，所以()()f x f x -=，由()()114f x f x ++-=，可得()f x 关于()1,2对称，因为()()114f x f x ++-=，所以()()13134f x f x ⎡⎤⎡⎤+++-+=⎣⎦⎣⎦，则()()()()41313424f x f x f x f x ⎡⎤⎡⎤⎡⎤+=++=--++=--++⎣⎦⎣⎦⎣⎦，因为()f x 是偶函数，所以()()22f x f x ⎡⎤--+=-+⎣⎦，因为()()114f x f x ++-=，所以()()11114f x f x ⎡⎤⎡⎤+++-+=⎣⎦⎣⎦，则()()()()()()42411411f x f x f x f x f x f x ⎡⎤⎡⎤+=-++=-+++=-+=-=⎣⎦⎣⎦，所以函数()f x 是周期为4的周期函数.因为()f x 是偶函数，且在[]0,1单调递增，所以()f x 在[]1,0-单调递减，令()()114f x f x ++-=中0x =，则()()114f f +=，则()12f =，又因为()f x 关于()1,2对称，所以()f x 在[]1,2上单调递增，[]2,3上单调递减，结合函数()f x 是周期为4的周期函数，综上可得()f x 在[]0,2，[]4,6上单调递增，[]2,4，[]6,8上单调递减.因为πsin 4y x =的最小正周期为2π8π4T ==，结合πsin 4y x =图象可知，πsin4y x =在[]0,2，[]6,8上单调递增，在[]2,6上单调递减，令()()114f x f x ++-=中1x =，则()()204f f +=，则()24f =，当π1,sin42x y ===，又()12f =，所以()π1sin 4f ⋅=，当3π23,sin42x y ===，又()()()3112f f f =-==，所以()3π3sin 4f ⋅=，所以当[]0,8x ∈时，π()sin 4xf x ⋅≥[]1,3x ∈.又因为()f x 与πsin 4y x =均为周期函数，且8均为其周期，所以π()sin4xf x ⋅≥x 的取值范围是[]18,38,Z k k k ++∈.故答案为：[]18,38,Z k k k ++∈.【点睛】本题解题的关键是求出()y f x =与πsin4y x =的周期性，由()π1sin 4f ⋅=，()3π3sin4f ⋅=，结合函数的单调性和周期性求解即可.11.若函数()sin cos 1sin cos f x a x b x b x a x =+-+-(,R a b ∈)的最大值为11，则22a b +=___________.【答案】50【解析】【分析】根据绝对值的几何意义圆的三角代换即可求解.【详解】())1)f x x x ϕϕ=+-++的几何意义为：以原点为为半径的圆周上点到1y =与到y 轴距离之和的最大值为11，故111=.所以2250a b +=.故答案为：50.12.已知n S 为数列{}n a 的前n 项和，数列{}n a 满足12a =-，且32n n S a n =+，()f x 是定义在R 上的奇函数，且满足()()2=f x f x -，则()2021f a =______．【答案】0【解析】【分析】利用数列通项公式与前n 项和公式的关系求通项的递推关系，再构造等比数列求出{}n a 通项公式.根据()()2=f x f x -和f (x )是R 上奇函数可得f (x )是周期为4的函数，且f (0)＝f (2)＝0.()20212021202131411a =-+=--+，将()202141-用二项式定理展开，其中能被4整除的部分在计算()2021f a 时即可“去掉”，由此即可求出答案.【详解】32n n S a n =+ ，()113122n n a n S n --∴=+-≥，两式相减得，133122n n n a a a -=-+，即()1311n n a a -=--，1131n n a a --∴=-，即数列{}1n a -是以3-为首项，3为公比的等比数列，11333n n n a -∴-=-⋅=-，31n n a ∴=-+.()f x 是定义在R 上的奇函数，且满足()()2=f x f x -，∴令2x =，则()()200f f ==，又()()2=f x f x -＝－f (－x )，∴f (2＋x )＝－f (x )，∴f (x ＋4)＝f (x ＋2＋2)＝－f (x ＋2)＝－[－f (－x )]＝f (x )，即f (x ＋4)＝f (x )，即()f x 是以4为周期的周期函数.()20212021202131411a =-+=--+ ()()()()120202021020211202020201202102021202120212021C 41C 41C 41C 411⎡⎤=-⋅-+⋅-++⋅-+⋅-+⎣⎦()()()012020020211202020201202120212021C 41C 41C 412⎡⎤=-⋅-+⋅-+⋅-+⎣⎦…+其中()()()12020020211202020201202120212021C 41C 41C 41⋅-+⋅-+⋅-…+能被4整除，()()()202120213120f a f f ∴=-+==.故答案为：0．【点睛】本题综合考察了数列求通项公式的两个方法：利用通项公式和前n 项和公式的关系，以及构造等比数列，考察了函数周期的求法，还考查了利用二项式定理处理整除问题，属于难题.二､单选题（本大题共4题，满分20分）13.已知实数a 、b ，那么||||||a b a b +=-是0ab <的（）条件．A.充分不必要B.必要不充分C.充要D.既不充分也不必要【答案】D 【解析】【分析】等式两边平方结合反例即可判断.【详解】因为2222||||||2|2|||0a b a b a ab b a ab b ab ab ab +=-⇒++=-+⇒=-⇒≤，所以必要性不成立；当1,2a b ==-时，满足0ab <，但||||||a b a b +≠-，所以充分性不成立；所以||||||a b a b +=-是0ab <的既不充分也不必要条件.故选:D ．14.设两个正态分布2111()(0)N μσσ>，和2222()(0)N μσσ>，的密度函数图像如图所示．则有A.1212,μμσσ<<B.1212,μμσσ<>C.1212,μμσσ><D.1212,μμσσ>>【答案】A 【解析】【详解】根据正态分布函数的性质：正态分布曲线是一条关于对称，在处取得最大值的连续钟形曲线；越大，曲线的最高点越底且弯曲较平缓；反过来，越小，曲线的最高点越高且弯曲较陡峭，选A ．15.在圆锥PO 中，已知高2PO =，底面圆的半径为4，M 为母线PB 的中点，根据圆锥曲线的定义，下列四个图中的截面边界曲线分别为圆、椭圆、双曲线及抛物线，下面四个命题，正确的个数为（）①圆的面积为4π；；③双曲线两渐近线的夹角正切值为34；④抛物线的焦点到准线的距离为455A.1个B.2个C.3个D.4个【答案】B 【解析】【分析】对于①，利用圆锥的几何性质确定圆的半径，即可求得圆的面积；对于②，结合圆锥的轴截面可求得椭圆的长轴长；对于③，建立平面直角坐标系，设双曲线方程，确定双曲线上的点的坐标，即可求得双曲线方程，进而求得双曲线两渐近线的夹角正切值；对于④，建立平面直角坐标系，设抛物线方程，确定抛物线上的点的坐标，即可求得参数，由此可判断出答案.【详解】对于①，M 为母线PB 的中点，因此截面圆的半径为底面圆的半径的12，即截面圆半径为2，则圆的面积为4π，故①正确；对于②，如图，在圆锥的轴截面PAB 中，作MC AB ⊥,垂足为C ，由题意可得M 为母线PB 的中点，则11,4262MC PO AC ===+=,故椭圆的长轴长为AM ===,②正确；对于③，如图，在与平面PAB 垂直且过点M 的平面内，建立平面直角坐标系，坐标原点与点P 到底面距离相等，则点M 坐标为(1,0)，双曲线与底面圆的一个交点为D ，其坐标为(2,，则设双曲线方程为22221,(0,0)x y a b a b-=>>，则1a =，将(2,代入双曲线方程，得224121,41b b-=∴=，设双曲线的渐近线b y x a =与x 轴的夹角为θ，则tan 2baθ==，故双曲线两渐近线的夹角正切值为224tan 2||143θ⨯==-，③错误；对于④，如图，建立平面直角坐标系，设抛物线与底面圆的一个交点为H ，则12OM PA ===4)H ,设抛物线方程为22,(0)y px p =>，则285425p p =∴=，即抛物线的焦点到准线的距离为5，④错误，故正确的命题有2个，故选：B16.如图，正四棱锥P ABCD -的底面边长和高均为2，M 是侧棱PC 的中点，若过AM 作该正四棱锥的截面，分别交棱PB ､PD 于点E ､F (可与端点重合)，则四棱锥P AEMF -的体积的取值范围是（）A.1,12⎡⎤⎢⎥⎣⎦ B.14,23⎡⎤⎢⎥⎣⎦C.41,3⎡⎤⎢⎣⎦D.8,19⎡⎤⎢⎥⎣⎦【答案】D 【解析】【分析】设,PE PFx y PB PD==,则,PE xPB PF yPD ==，然后利用等体积法由P AEMF P AEF P EMF V V V ---=+()223P AFM P AEMV V xy x y --=+==+，得到331y x y =-，再消元得到223331P AEMF y V y -=⋅-，令31y t -=，利用对勾函数的性质求解.【详解】设,PE PFx y PB PD==,则,PE xPB PF yPD ==所以412,323P AEF P ABD P MEF P BCD V xy V xy V xyV xy ----=⋅===，1212,2323P AFM P ACD P AEM P ABC V y V y V x V x ----=⋅==⋅=，()223P AEMF P AEF P EMF P AFM P AEM V V V V V xy x y -----=+=+==+，所以3x y xy +=，则331yx y =-，令31y t -=，因为1,12y ⎡⎤∈⎢⎥⎣⎦，所以1,22t ⎡⎤∈⎢⎥⎣⎦，所以()221311412,319992t y t y t t +⎛⎫⎡⎤==++∈ ⎪⎢⎥-⎝⎭⎣⎦，所以2238,13319P AEMF y V y -⎡⎤=⋅∈⎢⎥-⎣⎦，故选：D【点睛】方法点睛：求解棱锥的体积时，等体积转化是常用的方法，转化原则是其高易求，底面放在已知几何体的某一面上．求不规则几何体的体积，常用分割或补形的思想，将不规则几何体转化为规则几何体以便于求解．三､解答题（本大题共有5题，满分76分）17.在三棱锥A BCD -中，2AB AD BD ===，BC DC ==，2AC =.（1）求证：BD AC ⊥；（2）若P 为AC 上一点，且34AP AC =，求直线BP 与平面ACD 所成角的正弦值.【答案】（1）证明见解析；（2）437.【解析】【分析】（1）取BD 中点O ，连接AO ，OC ，证明BD ⊥平面AOC 即可；（2）首先证明AO ⊥平面BDC ，然后以射线OB ，OC ，OD 为x ，y ，z 正半轴建系，然后算出BP和平面ACD 的法向量即可得到答案.【详解】（1）取BD 中点O ，连接AO ，OC ，因为AB AD =，BC DC =，所以BD AO ⊥，BD OC ⊥，又因为AO OC O = ，所以BD ⊥平面AOC ，即BD AC ⊥.（2）由（1）得，BD ⊥平面AOC ，又因为BD ⊂平面BCD ，所以平面AOC ⊥平面BDC ，易得AO =，1OC =，所以222AO OC AC +=，即AO OC ⊥，又因为平面AOC I 平面BDC OC =，所以AO ⊥平面BDC ，如图所示，以射线OB ，OC ，OD 为x ，y ，z正半轴建系，(A ，()1,0,0B ，()0,1,0C ，()1,0,0D -，30,,44P ⎛⎫⎪ ⎪⎝⎭，31,44BP ⎛⎫=- ⎪ ⎪⎝⎭，DA =，(1,1,0)DC = ，设(,,)n x y z = 为平面ADC一个法向量，则有0000n DA x n DC x y ⎧⎧⋅=+=⎪⎪⇒⎨⎨⋅=+=⎪⎪⎩⎩，取(n =-，设θ为直线BP 与平面ACD 所成角，则9334344sin 7n BP n BPθ++⋅===⋅.即直线BP 与平面ACD所成角的正弦值为7.18.在△ABC 中，a ，b ，c 分别是内角A ，B ，C 的对边，()2,m a c b =+ ，()cos ,cos n B C =，0m n ⋅=.（1）求角B 大小；（2）设()()2π2cos sin 2sin sin 2sin cos cos 3f x x x x B x x A C ⎛⎫=+-++ ⎪⎝⎭，当2,63ππx ⎡⎤∈⎢⎥⎣⎦时，求()f x 的最小值及相应的x .【答案】（1）2π3B =（2）当7π12x =时，()f x 有最小值2-.【解析】【分析】（1）利用向量垂直的充要条件和正弦定理即可求解；（2）先利用两角和的正弦公式及余弦的二倍角公式化简，再用辅助角公式化为()π2sin 23f x x ⎛⎫=+ ⎪⎝⎭，最后利用三角函数的性质求出最小值及其取得最小值时的x 值.【小问1详解】由已知条件得()2cos cos 0m n a c B b C ⋅=++=，由正弦定理得()2sin sin cos sin cos 0A C B B C ++=，即2sin cos sin cos sin cos 0A B C B B C ++=，()2sin cos sin =0A B B C ++,则2sin cos sin 0A B A +=，∵sin 0A ≠，∴1cos 2B =-，又∵()0,πB ∈,∴2π3B =;【小问2详解】()()2π2cos sin 2sin sin 2sin cos cos 3f x x x x B x x A C ⎛⎫=+-++ ⎪⎝⎭212cos sin cos sin cos22x x x x x x ⎛⎫=+-+ ⎪ ⎪⎝⎭222sin cos x x x x =+-sin 22x x =+π2sin 23x ⎛⎫=+ ⎪⎝⎭,∵2,63ππx ⎡⎤∈⎢⎥⎣⎦,∴π2π5π2,333x ⎡⎤+∈⎢⎣⎦,π22sin 23x ⎛⎫-≤+≤ ⎪⎝⎭，则()f x 的最小值2-，其中π3π232x +=，即当7π12x =时，()f x 有最小值2-.19.一项试验旨在研究臭氧效应.实验方案如下：选40只小白鼠，随机地将其中20只分配到实验组，另外20只分配到对照组，实验组的小白鼠饲养在高浓度臭氧环境，对照组的小白鼠饲养在正常环境，一段时间后统计每只小白鼠体重的增加量（单位：g ）.（1）设X 表示指定的两只小白鼠中分配到对照组的只数，求X 的分布列和数学期望；（2）实验结果如下：对照组的小白鼠体重的增加量从小到大排序为：15.218.820.221.322.523.225.826.527.530.132.634.334.835.635.635.836.237.340.543.2实验组的小白鼠体重的增加量从小到大排序为：7.89.211.412.413.215.516.518.018.819.219.820.221.622.823.623.925.128.232.336.5（i ）求40只小鼠体重的增加量的中位数m ，再分别统计两样本中小于m 与不小于的数据的个数，完成如下列联表：m<m≥对照组实验组（ii ）根据（i ）中的列联表，能否有95%的把握认为小白鼠在高浓度臭氧环境中与正常环境中体重的增加量有差异．附：()()()()22(),n ad bc K a b c d a c b d -=++++0k 0.1000.0500.010()20P K k ≥ 2.7063.8416.635【答案】（1）分布列见解析，()1E X=（2）（i）23.4m=；列联表见解析，（ii）能【解析】【分析】（1）利用超几何分布的知识即可求得分布列及数学期望；（2）（i）根据中位数的定义即可求得23.4m=，从而求得列联表；（ii）利用独立性检验的卡方计算进行检验，即可得解.【小问1详解】依题意，X的可能取值为0,1,2，则022020240C C19(0)C78P X===，12022401C C20(1)C39P X===，202020240C C19(2)C78P X===，所以X的分布列为：X012P 197820391978故192019 ()0121783978E X=⨯+⨯+⨯=.【小问2详解】（i）依题意，可知这40只小白鼠体重增量的中位数是将两组数据合在一起，从小到大排后第20位与第21位数据的平均数，观察数据可得第20位为23.2，第21位数据为23.6，所以23.223.623.42m+==，故列联表为：m<m≥合计对照组61420实验组14620合计202040（ii ）由（i ）可得，2240(661414) 6.400 3.84120202020K ⨯⨯-⨯==>⨯⨯⨯，所以能有95%的把握认为小白鼠在高浓度臭氧环境中与正常环境中体重的增加量有差异.20.已知点12F F 、为双曲线()222210,0x y a b a b-=>>的左右焦点，过2F 作垂直于x 轴的直线，在x 轴上方交双曲线于点M ，且121230,MF F MF F ∠=︒△的面积为.圆O 的方程是222x y r +=.（1）求双曲线的方程；（2）过双曲线上任意一点P 作该双曲线两条渐近线的垂线，垂足分别为12P P 、，求12PP PP ⋅的值；（3）过圆O 上任意一点Q 作圆O 的切线l 交双曲线C 于A B 、两点，AB 中点为N ，若||2||AB ON =恒成立，试确定圆O 半径r .【答案】（1）22124x y -=；（2）49；（3）2r =.【解析】【分析】（1）由面积可求c =，再根据双曲线的定义可求a ，从而可求双曲线的方程；（2）求出双曲线的渐近线方程，设两渐近线的夹角为θ，根据到角公式可求tan θ与cos θ，根据点到直线的距离公式可求12,PP PP ，根据平面向量的数量积运算结合00(,)P x y 在双曲线22124x y -=上即可求解；（3）由题意可得OA OB ⊥，设11(,)A x y ，22(,)B x y ，当l 的斜率存在时，设直线:l y kx b =+，与双曲线方程联立，根据韦达定理及0OA OB ⋅=可得2244b k =+，根据点到直线的距离公式可求2r =，当l 的斜率不存在时亦可求得.【小问1详解】因为121230,MF F MF F ∠=︒△的面积为2MF =所以122c ⋅=c =22a ==，所以2224a b c a ==-=，故双曲线的方程为22124x y -=.【小问2详解】由题意得两条渐近线分别为120;0l y l y -=+=，设双曲线C 上的点00(,)P x y ，设两渐近线的夹角为θ，则tan θ==，得1cos 3θ==．则点P到两条渐近线的距离分别为12PP PP ==，因为00(,)P x y 在双曲线22124x y -=上，所以220024x y -=，又1cos 3θ=，所以22001221cos 3394x y PP PP θ-⋅===.【小问3详解】AB 中点为N ，若||2||AB ON =，则OA OB ⊥．设11(,)A x y ，22(,)B x y ，当l 的斜率存在时，设直线:l y kx b =+，由22124x y y kx b ⎧-=⎪⎨⎪=+⎩得()2222240k x kbx b ----=，所以212122224,22kb b x x x x k k --+==--，所以()()12121212OA OB x x y y x x kx b kx b =⋅=++++()()22121201k x x kb x x b =++++=，所以()22222421022b kb k kb b k k--+⋅+⋅+=--，所以()()()22222214220kbk b k b +--++-=，所以2224420b k b ---+=，所以2244b k =+,2=.当l 的斜率不存在时，直线2x =±，得2y =±，也满足OA OB ⊥，综上，圆O 半径2r =．【点睛】解决直线与双曲线的综合问题时，要注意：(1)注意观察应用题设中的每一个条件，明确确定直线、双曲线的条件；(2)强化有关直线与双曲线联立得出一元二次方程后的运算能力，重视根与系数之间的关系、弦长、斜率、三角形的面积等问题．21.已知()f x 是定义在[],a b 上的函数，如果存在常数0M >，对区间[],a b 的任意划分：011n n a x x x x b -=<<<<=L ，和式()()11ni i i f x f x M -=-≤∑恒成立，则称()f x 为[],a b 上的“绝对差有界函数”，注：121nin i aa a a ==+++∑ .（1）求证：函数()sin cos f x x x =+在,02p轾-犏犏臌上是“绝对差有界函数”；（2）记集合(){|A f x =存在常数0k >，对任意的[]12,,x x a b ∈，有()()1212f x f x k x x -≤-成立.求证：集合A 中的任意函数()f x 为“绝对差有界函数”；（3）求证：函数()cos,01{20,0x x f x xx π<≤==不是[]0,1上的“绝对差有界函数”.【答案】（1）见解析（2）见解析（3）见解析【解析】【分析】（1）将()f x整理为4x π⎛⎫+⎪⎝⎭，可知()f x 在,02π⎡⎤-⎢⎥⎣⎦上单调递增；可知()()1i i f x f x +<，从而可将()()11ni i i f x f x -=-∑化简为()022f f π⎛⎫--= ⎪⎝⎭，从而可知()()112nii i f x f x -=-≤∑，得到结论；（2）取()f x A ∈，根据()()1212f x f x k x x -≤-，可得()()()1111nnii ii i i f x f x k x xk b a --==-≤-=-∑∑，从而可取()M k b a =-得到结论；（3）取一个划分：111012212n n <<<⋯<<-，可将()()11n i i i f x f x -=-∑整理为11ni i=∑；根据放缩可知只要n 足够大，可使得()()11nii i f x f x M -=->∑，从而得到结论.【详解】（1）()sin cos 4f x x x x π⎛⎫=+=+ ⎪⎝⎭当,02x ⎡⎤∈-⎢⎥⎣⎦π时，,444x πππ⎡⎤+∈-⎢⎥⎣⎦()f x \在区间,02π⎡⎤-⎢⎥⎣⎦上为单调递增函数∴当1i i x x +<，0,1,2,,1i n =⋅⋅⋅-时，有()()1i i f x f x +<，0,1,2,,1i n =⋅⋅⋅-所以()()()()()1111022nni i i i i i f x f x f x f x f f π--==⎛⎫-=-=--=⎡⎤ ⎪⎣⎦⎝⎭∑∑从而对区间,02π⎡⎤-⎢⎥⎣⎦的任意划分：01102n n x x x x π--=<<<<=L 存在2M =，使得()()112nii i f x f x -=-≤∑成立综上，函数()sin cos f x x x =+在,02π⎡⎤-⎢⎥⎣⎦上是“绝对差有界函数”（2）证明：任取()f x A∈从而对区间[],a b 的任意划分：011n n a x x x x b -=<<⋯<<=和式()()()1111n nii ii i i f x f x k x xk b a --==-≤-=-∑∑成立则可取()Mk b a =-所以集合A 中的任意函数()f x 为“绝对差有界函数”（3）取区间[]0,1的一个划分：111012212n n <<<⋯<<-，*n ∈N 则有：()()()211211211212cos 0cos cos cos cos 2221222222ni i i n n n f x f x n n n πππππ-=--=-+-+⋅⋅⋅+--∑1481111111111111244881616222ni i=↑↑=>+++++⋅⋅⋅+++⋅⋅⋅++⋅⋅⋅=+++⋅⋅⋅++⋅⋅⋅∑所以对任意常数0M >，只要n 足够大，就有区间[]0,1的一个划分：111012212n n <<<⋯<<-满足()()11ni i i f x f x M-=->∑所以函数()cos ,0120,0x x f x xx π⎧<≤⎪=⎨⎪=⎩不是[]0,1的“绝对差有界函数”【点睛】本题考查与新定义有关的证明问题，关键是能够理解新定义的具体含义，进而可通过单调性、不等关系、放缩的方式把关系式进行化简，从而可求得临界值的具体取值，再根据取值确认函数是否符合新定义，属于难题.。

第二中学2021届高三数学下学期开学考试试卷文本卷贰O贰贰年贰月捌日编写；出题人：令狐学复；欧阳化语；令狐理总。

一、选择题〔本大题一一共12小题，一共分〕1.设集合，，那么等于A. {}3>x xB. RC.D.2.设复数z满足，那么A. B. C. D. 23.偶函数在区间单调递增，那么满足的x取值范围是A. B. C. D.4.方程表示双曲线的一个充分不必要条件是A. B.B.C. D.5.中国古代有计算多项式值的秦九韶算法，如图是实现该算法的程序框图执行该程序框图，假设输入的，，依次输入的a为2，2，5，那么输出的s= )A. 7B. 12C. 17D. 346.是边长为2的等边三角形，P为平面ABC内一点，那么的最小值是A. B.C.D.7. 某几何体的三视图如下图，那么该几何体的体积为A. 12B. 18C. 24D. 308. 等差数列的前n 项和为，且，，那么使取最小值时的n 为A. 1B. 6C. 7D. 6或者79.，x ，y 满足约束条件，的最小值为，那么A.B.C. 1D. 2 10. 双曲线C ：的左、右焦点分别为，，P 是双曲线C 右支上一点，且假设直线与圆相切，那么双曲线的离心率为 A. B.C. 2D. 311.，将的图象向右平移个单位，再向上平移1个单位，得到的图象假设对任意实数x ，都有成立，那么A.B. 1C.D. 012. 函数)(x f 的定义域为R ，且xxe x f x f -=+'2)()(，假设f(0)=1，那么函数)()(x f x f '的取值范围为〔 〕A. ]1,0[B. ]2,0[C. ]0,1[-D. ]0,2[-二、填空题〔本大题一一共4小题，一共分〕 13. 函数，是偶函数，那么______．14. 三棱锥的三条侧棱两两互相垂直，且，，那么此三棱锥外接球的外表积为__________．15. 锐角三角形ABC 中，角A,B,C 的 对边分别为a,b,c ，假设b 2=a(a+c), 那么ac的取值范围为 .16. 在平面直角坐标系xOy 中，双曲线的右支与焦点为F 的抛物线交于A ，B 两点，假设，那么该双曲线的渐近线方程为_________．三、解答题〔本大题一一共7小题，一共70分〕 17.(此题满分是12分) 各项均为正实数的数列的前n 项和为，对于一切成立．Ⅰ求；Ⅱ求数列的通项公式；Ⅲ设为数列的前n 项和，求证．18. (此题满分是12分)某校高三举行了一次数学竞赛，为了理解本次竞赛学生的成绩情况，从中抽取了局部学生的分数得分取正整数，满分是为作为样本样本容量为进展统计，按照，，，，的分组作出频率分布直方图，得分在，的频数分别为8，2．求样本容量n 和频率分布直方图中的x ，y 的值； 估计本次竞赛学生成绩的中位数；在选取的样本中，从竞赛成绩在80分以上含80分的学生中随机抽取2名学生，求所抽取的2名学生中至少有一人得分在内的概率．19.(此题满分是12分)如图，三棱柱中，侧面为菱形，的中点为O，且平面C.证明：；假设，，，求三棱柱的高．20. (此题满分是12分)设椭圆的左焦点为F，右顶点为A，离心率为A是抛物线的焦点，F到抛物线的准线l的间隔为．求椭圆的方程和抛物线的方程；设l上两点P，Q关于x轴对称，直线AP与椭圆相交于点异于，直线BQ与x轴相交于点假设的面积为，求直线AP的方程．21. (此题满分是12分)函数，其中e是自然对数的底数．假设，求函数在上的最大值；假设，关于x的方程有且仅有一个根，务实数k的取值范围；假设对任意的、，，不等式都成立，务实数a的取值范围．请考生在第22,23题中任选一题做答，假如多做，那么按所做的第一题计分，做答时请写清题号22.(此题满分是10分) 曲线C 的参数方程为为参数，以直角坐标系原点O 为极点，x轴正半轴为极轴建立极坐标系．Ⅰ求曲线C 的极坐标方程；Ⅱ设 6:1πθ=l ，3:2πθ=l ，假设、与曲线C 相交于异于原点的两点A 、B ，求的面积．23. (此题满分是10分)函数．Ⅰ求不等式的解集；Ⅱ假设关于x 的不等式有解，务实数m 的取值范围．高三数学〔文〕答案一、选择题：题号 1 2 3 4 5 6 7 8 9 10 11 12答案 D C A A C B C B B B B D二、填空题：13.4 14. 8 15.(1, 2) 16.三、解答题〔本大题一一共7小题，一共70分〕的前n项和为，对于一切成立．Ⅰ求；Ⅱ求数列的通项公式；Ⅲ设为数列的前n项和，求证．【答案】解：Ⅰ当时，，，得，或者，由条件，所以．Ⅱ当时，，；那么，所以，，，由条件，所以，故正实数列是首项为3，公差为2的等差数列，所以Ⅲ由Ⅰ，，，将上式两边同乘以，得，得，即．，．18.某校高一举行了一次数学竞赛，为了理解本次竞赛学生的成绩情况，从中抽取了局部学生的分数得分取正整数，满分是为作为样本样本容量为进展统计，按照，，，，的分组作出频率分布直方图，得分在，的频数分别为8，2．求样本容量n和频率分布直方图中的x，y的值；估计本次竞赛学生成绩的中位数；在选取的样本中，从竞赛成绩在80分以上含80分的学生中随机抽取2名学生，求所抽取的2名学生中至少有一人得分在内的概率．【答案】本小题满分是12分解：由题意可知，样本容量，．设本次竞赛学生成绩的中位数为m，那么，解得，本次竞赛学生成绩的中位数为71．由题意可知，分数在内的学生有5人，记这5人分别为，，，，，分数在内的学生有2人，记这2人分别为，．抽取的2名学生的所有情况有21种，分别为：，，，，，，，，，，，，，，，，，，，，其中2名同学的分数都不在内的情况有10种，分别为：，，，，，，，，，所抽取的2名学生中至少有一人得分在内的概率．19.如图，三棱柱中，侧面为菱形，的中点为O，且平面C.证明：；假设，，，求三棱柱的高．【答案】证明：连接，那么O为与的交点，侧面为菱形，，平面，，，平面ABO，平面ABO，；解：作，垂足为D，连接AD，作，垂足为H，，，，平面AOD，，，，平面ABC，，为等边三角形，，，，，由，可得，，为的中点，根据相似性到平面ABC的间隔为，三棱柱的高．的左焦点为F，右顶点为A，离心率为A是抛物线的焦点，F到抛物线的准线l的间隔为．求椭圆的方程和抛物线的方程；设l上两点P，Q关于x轴对称，直线AP与椭圆相交于点异于，直线BQ与x轴相交于点假设的面积为，求直线AP的方程．【答案】Ⅰ解：设F的坐标为．依题意可得，解得，，，于是．所以，椭圆的方程为，抛物线的方程为Ⅱ解：直线l的方程为，设直线AP的方程为，联立方程组，解得点，故联立方程组，消去x，整理得，解得，或者．直线BQ的方程为，令，解得，故D．．又的面积为，，整理得，解得，．直线AP的方程为，或者．，其中e是自然对数的底数．假设，求函数在上的最大值；假设，关于x的方程有且仅有一个根，务实数k的取值范围；假设对任意的、，，不等式都成立，务实数a的取值范围．【答案】解：假设，那么，，时，，时， 0'/>，函数在区间上单调递减，在区间上单调递增，又，故函数的最大值为．由题意得：有且只有一个根，令，那么故在上单调递减，上单调递增，上单调递减，所以，因为在单调递减，且函数值恒为正，又当时，，所以当时，有且只有一个根．设，因为在单调递增，故原不等式等价于在、，且恒成立，所以在、，且恒成立，即，在、，且恒成立，那么函数和都在单调递增，那么有，在恒成立，当恒成立时，因为在单调递减，所以的最大值为，所以；当恒成立时，因为在单调递减，在单调递增，所以的最小值为，所以，综上：．C的参数方程为为参数，以直角坐标系原点O为极点，x轴正半轴为极轴建立极坐标系．Ⅰ求曲线C的极坐标方程；Ⅱ设：，假设、与曲线C相交于异于原点的两点A、B ，求的面积．【答案】解：Ⅰ曲线C的普通方程为，将代入得：Ⅱ由，解得，解得23函数．Ⅰ求不等式的解集；Ⅱ假设关于x的不等式有解，务实数m的取值范围．【答案】解：Ⅰ不等式，即，可化为或者或者，分解得，解得，解得，综合得：，即原不等式的解集为分Ⅱ因为，当且仅当时，等号成立，即，分又不等式有解，那么，解得：或者分本卷贰O贰贰年贰月捌日编写；出题人：令狐学复；欧阳化语；令狐理总。

2022-2023学年高三下学期开学考试数学（文科）试卷一、单选题（本大题共12小题，共60.0分。

在每小题列出的选项中，选出符合题目的一项）1. 设集合A={x|−2<x<4}，B={2,3,4,5}，则A∩B=( )A. {2,3,4}B. {3,4}C. {2,3}D. {2}2. 已知a,b∈R，i是虚数单位，若(a+i)(1+i)=bi，则a+bi=( )A. −1+2iB. 1+2iC. 1−2iD. 1+i3. 已知向量a⃗，b⃗均为单位向量，若它们的夹角是60°，则|a⃗−3b⃗|等于( )A. √7B. √10C. √13D. 44. 已知在△ABC中，cos(A−π6)=−13，那么sin(A+π6)+cosA等于( )A. −√33B. √33C. −2√33D. 2√335. 根据有关资料，围棋状态空间复杂度的上限M约为3361，而可观测宇宙中普通物质的原子总数N约为1080.则下列各数中与MN最接近的是(参考数据：lg3≈0.48)( )A. 1033B. 1053C. 1073D. 10936. 函数f(x)=12x2−xsin x的大致图象可能是( )A. B. C. D.7. 已知为等比数列，，，则A. B. C. D. 8. 如图，正方体ABCD−A1B1C1D1的棱长为2，线段D1B1上有两个动点E、F，且EF=√2，则下列结论中错误的是( )A. AA1//平面BEFB. 三棱锥E−FAB的体积为定值C. 二面角A−EF−C的余弦值为13D. 当EF⃗⃗⃗⃗⃗ =2FB1⃗⃗⃗⃗⃗⃗⃗⃗ 时，点A到E的距离为√69. “湖畔波澜飞，耕耘战鼓催”，合肥一六八中学的一草一木都见证了同学们的成长.某同学为了测量澜飞湖两侧C，D两点间的距离，除了观测点C，D外，他又选了两个观测点P1，P2，且P1P2=a，已经测得两个角∠P1P2D=α，∠P2P1D=β，由于条件不足，需要再观测新的角，则利用已知观测数据和下面三组新观测的角的其中一组，就可以求出C，D间距离的有组( )①∠DP1C和∠DCP1；②∠P1P2C和∠P1CP2；③∠P1DC和∠DCP1A. 0B. 1C. 2D. 310. 定义在R上的函数f(x)满足：f′(x)>1−f(x)，f(0)=6，f′(x)是f(x)的导函数，则不等式e x f(x)>e x+5(其中e为自然对数的底数)的解集为( )A. (0,+∞)B. (−∞,0)∪(3,+∞)C. (−∞,0)∪(1,+∞)D. (3,+∞)11. 已知椭圆x2a2+y2b2=1(a>b>0)的左右焦点分别是F1,F2，焦距为2c，若直线y=√3(x+c)与椭圆交于M点，且满足∠MF1F2=2∠MF2F1，则椭圆的离心率是( )A. √22B. √3−1C. √3−12D. √3212. 已知侧棱长为2√3的正四棱锥各顶点都在同一球面上．若该球的表面积为36π，则该正四棱锥的体积为 A.163B.8√23C. 83D.323二、填空题（本大题共4小题，共20.0分）13. 设等差数列{a n }的前n 项为S n ，若a 3=8，S 4=26，则公差d =________． 14. 已知实数x ，y 满足约束条件{x −2≥02x +y −7≤0x −y −2≤0，则z =3x +4y 的最大值是______．15. 已知f(x)是定义在R 上的偶函数，且f(x +4)=f(x −2).若当x ∈[−3,0]时，f(x)=6−x ，则f(919)= ．16. 已知点M(1,2)，点P 是双曲线C ：x 29−y216=1左支上的动点，F 2为其右焦点，N 是圆D ：(x +5)2+y 2=1的动点，则|PM|−|PN|的最小值为 ．三、解答题（本大题共6小题，共70.0分。

济南2024届高三开学摸底考语文真题及答案解析山东省济南市2024届高三下学期开学考试语文试题注意事项：1.本试卷满分150分，考试时间150分钟。

2.答卷前，考生务必将自己的姓名、座号、考生号填写在答题卡上，并将条形码横贴在答题卡的“贴条形码区”。

3.作答选择题时，选出每小题答案后，用2B铅笔把答题卡上对应题目选项的答案信息点涂黑;如需改动，用橡皮擦干净后，再选涂其他答案，答案不能答在试卷上。

4.非选择题必须用直径0.5毫米黑色字迹钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上;如需改动，先划掉原来的答案，然后再写上新的答案;不准使用铅笔和涂改液，不按以上要求作答的答案无效。

5.考生必须保持答题卡的整洁。

考试结束后，将试卷和答题卡一并交回。

一、现代文阅读(35分)(一)现代文阅读I(本题共5小题，19分)阅读下面的文字，完成1-5题材料一：我国自古就有声诗统一的传统，从艺术起源看，诗、乐、舞三位一体，在先秦时期便是如此。

《诗经》与《楚辞》实则都是可以演唱的歌词。

到两汉和魏晋南北朝时期，乐府诗还是可以演唱的，甚至唐代时，还有乐工可以歌唱汉魏乐府诗。

到了唐代，除了乐府诗以外，一部分或五言、或七言的近体诗(律诗和绝句)也可以演唱。

但唐代大部分的诗都不能演唱了。

宋诗不能唱，代之而起的是可以演唱的词。

元代又有了可以演唱的曲子，即套曲和小令。

诗词既然能唱，就应该有乐谱。

现在我们能够见到的最早乐谱是在敦煌藏经洞里发现的唐代琵琶乐谱和现藏于日本阳明文库的原近卫家所藏唐五弦琵琶谱，但都有谱无诗。

南宋朱熹《仪礼经传通解》收录的南宋赵彦肃传的《风雅十二诗谱》，是为《诗经》所配的曲子。

如果确实是唐开元年间传下来的诗谱的话，它应该是流传下来的最早的声诗兼备的诗谱，即最早的诗歌曲。

中国古代曲谱都有曲与歌词同载的习惯，唐宋以来有文字谱、减字谱、俗字谱、律吕谱、工尺谱等复杂的记谱法。

南宋姜夔曾把唐代名曲《霓裳曲》中的两段曲谱破译成当时流行的俗字谱，以便时人歌唱。

高三文科数学考生注意：1.本试卷分选择题和非选择题两部分.满分150分，考试时间120分钟.2.答题前，考生务必用直径0.5毫米黑色墨水签字笔将密封线内项目填写清楚.3.考生作答时，请将答案答在答题卡上，选择题每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑；非选择题请用直径0.5毫米黑色墨水签字笔在答题卡上各题的答题区域内作答，超出答题区域书写的答案无效，在试题卷､草稿纸上作答无效.4.本试卷主要命题范围：高考范围.一､选择题：本题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.已知集合{}2M x y x ==+，{}53N x x =-<<，则MN =（）A.{}23x x -<≤B.{}5x x >- C.{}3x x < D.{}52x x -<-≤ 2.复数312ii z -=在复平面内对应的点位于（） A.第一象限B.第二象限 C.第三象限D.第四象限3.已知函数()2ln f x ax x =-的图象在点()()1,1f 处的切线与直线3y x =-平行，则该切线的方程为（）A.210x y ++=B.330x y +-=C.320x y +-=D.210x y +-=4.我国传统剪纸艺术历史悠久，源远流长，最早可追潮到西汉时期.下图是某一窗花的造型，在长为3，宽为2的矩形中有大小相同的两个圆，两圆均与矩形的其中三边相切，在此矩形内任取一点，则该点取自两圆公共（图中阴影）部分的概率为（）A.31824π-B.31216π-C.3912π- D.368π-5.古代名著《九章算术》中记载了求“方亭”体积的问题，方亭是指正四棱台，今有一个方亭型的水库，该水库的下底面的边长为20km ，上底面的边长为40km ，若水库的最大蓄水量为932810m 3⨯，则水库深度（棱台的高）为（） A.10m B.20m C.30m D.40m6.已知抛物线C ：()220y px p =>，过焦点F 的直线4340x y +-=与C 在第四象限交于M 点，则MF =（） A.3B.4C.5D.67.执行如图所示的程序框图，则输出的k 的值为（）A.14B.15C.16D.178.某部门统计了某地区今年前7个月在线外卖的规模如下表： 月份代号x1 2 3 4 5 6 7 在线外卖规模y （百万元）111318★28★35其中4､6两个月的在线外卖规模数据模糊，但这7个月的平均值为23.若利用回归直线方程y bx a =+来拟合预测，且7月相应于点()7,35的残差为-0.6，则ˆˆab -=（） A.1.0B.2.0C.3.0D.4.09.已知等比数列{}n a 的前4项和为30，且54314a a a =-，则9a =（） A.14B.18C.116D.13210.记函数()()2cos 0,2f x x b πωϕωϕ⎛⎫=++><⎪⎝⎭的最小正周期为T ，若24T f ⎛⎫=-⎪⎝⎭，且函数()f x 的,36π⎛⎫- ⎪⎝⎭对称，则当ω取得最小值时，8f π⎛⎫= ⎪⎝⎭（） A.2B.1C.-1D.-211.已知双曲线C ：()222210,0x y a b a b-=>>的左焦点为F ，过F 的直线与C 的两条渐近线分别交于A ，B 两点，与C 交于P ，Q 两点，若P ，F ，Q 四等分线段AB ，则C 的离心率为（）A.33D.12.已知球O 的半径为2，四棱锥的顶点均在球O 的球面上，当该四棱锥的体积最大时，其高为（） A.53B.2C.73D.83二､填空题：本题共4小题，每小题5分，共20分.13.已知向量()1,2m a a =-+-，()3,4n a a =-+，若()m n m +∥，则实数a =___________.14.记n S 为等差数列{}n a 的前n 项和，已知1233a a a +-=，34511a a a +-=，则n S =___________.15.写出与圆()2211x y -+=和()()22134x y -+-=都相切的一条直线的方程___________. 16.已知函数()3ln22a f x x b x ⎛⎫=-- ⎪-⎝⎭（a ，b ∈R 且0a ≠）是偶函数，则a =___________，b =___________.（本题第1问2分，第2问3分）三､解答题：共70分.解答应写出文字说明､证明过程或演算步骤.第17~21题为必考题，每个试题考生都必须作答.第22､23题为选考题，考生根据要求作答. （一）必考题：共60分.17.（12分）已知△ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，()sin tan sin sin B C A B C -=. （1）若A B =，求2sin A 的值；（2）证明：222a b c +为定值.18.（12分）青少年近视问题备受社会各界广泛关注，某研究机构为了解学生对预防近视知识的掌握情况，对某校学生进行问卷调查，并随机抽取200份问卷，发现其得分（满分：100分）都在区间[]50,100中，并将数据分组，制成如下频率分布表：（1）估计这200份问卷得分的平均值（同一组中的数据用该组区间的中点值代表）；（2）用分层抽样的方法从这200份问卷得分在[)70,80，[)80,90，[]90,100内的学生中抽取6人，再从这6人中随机抽取3人进行调查，求这3人来自不同组（3人中没有2人在同一组）的概率.19.（12分）如图，在四棱锥P -ABCD 中，PD ⊥底面ABCD ，AB AD ⊥，4AB =，2AD =，23BC =，6CD =.（1）证明：平面PCD ⊥平面PBC ； （2）若4PD =，求三棱锥P -ABC 的体积. 20.（12分）已知函数()33xf x xe x x =-+.（1）求函数()f x 的单调区间； （2）当13x ≥时，()26f x ax x +≥恒成立，求实数a 的取值范围. 21.（12分）已知椭圆E 的中心为坐标原点O ，对称轴分别为x 轴､y 轴，且过A （-1，0），212B ⎛⎫- ⎪ ⎪⎝⎭两点. （1）求E 的方程；（2）设F 为椭圆E 的一个焦点，M ，N 为椭圆E 上的两动点，且满足0MN AF ⋅=，当M ，O ，N 三点不共线时，求△MON 的面积的最大值.（二）选考题：共10分.请考生在第22､23题中任选一题作答.如果多做，则按所做的第一题计分.22.[选修4-4：坐标系与参数方程]（10分）在直角坐标系xOy 中，曲线C 的参数方程为11323133t t t t x y ⎧⎛⎫=+ ⎪⎪⎪⎝⎭⎨⎪=-⎪⎩（t 为参数），以坐标原点为极点，x轴正半轴为极轴建立极坐标系，已知直线l 的极坐标方程为cos sin 10m ρθρθ+-=. （1）求曲线C 的普通方程；（2）若l 与C 有两个不同公共点，求m 的取值范围.23.[选修4-5：不等式选讲]（10分） 已知函数()112f x x x =-++. （1）求不等式()3f x ≤的解集；（2）设函数()2g x x a x =-+-，若对任意1x ∈R ，都存在2x ∈R ，使得()()12f x g x =成立，求实数a 的取值范围.高三文科数学参考答案､提示及评分细则1.B {}{}22,{53}M xy x x x N x x ==+=-=-<<∣∣∣，所以{5}M N x x ⋃=>-∣.故选B.2.A 312i 12i 2i i i z --===+-，所以复数312i iz -=在复平面内对应的点为()2,1.故选A. 3.C ()12f x ax x'=-，则()1213f a -'==-，解得1a =-，所以()11f =-，则该切线的方程为()131y x +=--，即320x y +-=.故选C.4.C 如图所示，设两圆的圆心分别为12,O O ，两圆相交于,A B 两点，则两圆互过圆心，连接111222,,,,,,O A O B O O O A O B AB AB 与12O O 交于C ，则12111,1,2O O AB O A O C ⊥==，所以160AO C ∠=，则21120AO B AO B ∠∠==，所以弓形2AO B 的面积为211131332234S ππ=⨯⨯-⨯⨯=-，在矩形内任取一点，该点取自两圆公共部分的概率为3234332912p ππ⎛⎫⨯- ⎪⎝⎭==-⨯.故选C.5.A 设水库深度为km h ，由题意，(22221282040204033h ++⨯⋅=，解得0.01km h =，即10m h =.故选A.6.C 由题意可知，F 的坐标为()1,0，则12p=，所以2p =，则抛物线C 的方程为24y x =，设(00,2M x x -，由00243MF x k -==-，解得04x =，所以052p MF x =+=.故选C.7.B 由题知111111,152231S k k k ⎛⎫⎛⎫⎛⎫=-+-++-= ⎪ ⎪ ⎪+⎝⎭⎝⎭⎝⎭时，111111514122315161615S ⎛⎫⎛⎫⎛⎫=-+-++-=> ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，开始出现1415S >，故输出的k 的值为15.故选B. 8.B ()112345674,237x y =++++++==，所以ˆˆ423b a +=.因为相应于点()7,35的残差为0.6-，则点()7,35.6在回归直线ˆˆˆy bx a =+上，即ˆˆ735.6b a +=，解得ˆˆ 6.2, 4.2ab ==，则ˆˆ 2.0ab -=.故选B. 9.C 设等比数列{}n a 的公比为q ，前n 项和为n S ，由54314a a a =-，得214q q =-，解得12q =，由414112112a S ⎡⎤⎛⎫-⎢⎥ ⎪⎝⎭⎢⎥⎣⎦==-30，解得116a =，所以891116216a ⎛⎫=⨯= ⎪⎝⎭.故选C. 10.D 由题意可知，2,3T b πω==-，由24T f ⎛⎫=- ⎪⎝⎭，得2cos 322πϕ⎛⎫+-=- ⎪⎝⎭，所以1sin 2ϕ=-，因为2πϕ<，所以6πϕ=-，又函数()f x 的图象关于点,36π⎛⎫- ⎪⎝⎭对称，所以,662k k ωππππ-=+∈Z ，所以64,k k =+∈Z ，因为0ω>，所以当0k =时，ω取得最小值4，则()2cos 436f x x π⎛⎫=-- ⎪⎝⎭，故2cos 32826f πππ⎛⎫⎛⎫=--=- ⎪ ⎪⎝⎭⎝⎭.故选D. 11.A 不妨设交点的顺序自上而下为,,,A P Q B ，则AP PF FQ QB ===，由对称性可知，AB x ⊥轴，则AB 的方程为x c =-，代入b y x a =-，求得,bc A c a ⎛⎫- ⎪⎝⎭，代入22221x ya b -=，求得2,b P c a ⎛⎫- ⎪⎝⎭，则22,bc b b AP PF a a-==，所以22bc b b a a -=，所以2c b =，则a =，所以C 的离心率为3c e a ===.故选A. 12.D 四棱锥的底面内接于圆，当底面为正方形时，底面面积最大（论证如下：设底面四边形ABCD 的外接圆半径为r ，AC 与BD 的夹角为α，则四边形ABCD 的面积2111sin 222222S AC BD AC BD r r r α=⋅⋅⨯⨯=，当且仅当四边形ABCD 是正方形时，四边形ABCD 的面积取到最大值22r ）.要使四棱锥的体积最大，则从顶点作底面的垂线过球心O ，该四棱锥为正四棱锥，设底面的边长为a ，四棱锥的高为h ，底面外接圆的半径为2r a ==，由题意可知，22(2)4r h +-=，即221(2)42a h +-=，所以()2224a h h =-，则04h <<，四棱锥的体积为()22312433V a h h h =⨯=-，令()234(04)f x x x x =-<<，则()283f x x x -'=，由()0f x '=，得83x =，由80,3x ⎛⎫∈ ⎪⎝⎭，得()0f x '>，由8,43x ⎛⎫∈ ⎪⎝⎭，得()0f x '<，所以()f x 在80,3⎛⎫⎪⎝⎭上单调递增，在8,43⎛⎫ ⎪⎝⎭上单调递减，则当83x =时，()f x 取得极大值，也就是最大值，此时83h =.故选D. 13.54()2,6m n +=，由()m n m +∥，得()()61220a a -+--=，解得54a =. 14.225n n +设等差数列{}n a 的公差为d ，由1233453,11a a a a a a +-=+-=两式相减得28d =，解得4d =，由(()111)23a a d a d ++-+=，得17a =，故()2174252n n n S n n n -=+⨯=+.15.3y =--或3y =--+或1y =（答案不唯一，3个中任填一个即可）易知圆22(1)1x y -+=和22(1)(3)4x y -+-=外切，显然1y =与这两圆都相切.设直线y kx b=+与圆22(1)1x y -+=和22(1)(3)4x y -+-=1=2=，所以23k b k b +=+-，令k b t +=，则2230t t +-=，解得1t =或3t =-，当1t =时，解得0k =，此时1b =，直线方程即为1y =；当3t =-3=，解得k =±，当k =3b =--；当k =-3b =-+，所以直线方程为3y =--或3y =--+.16.8ln2易知3y x =是奇函数，因为函数()3ln22af x x b x ⎛⎫=-- ⎪-⎝⎭是偶函数，所以()ln22ag x b x=---是奇函数，又知2x ≠，根据奇函数的定义域关于原点对称，则2x ≠-，当2x =-时，204a-=，所以8a =，所以()824ln 2ln 22x g x b b x x +=--=---，则()040ln020g b +=-=-，解得ln2b =.经检验，8,ln2a b ==时符合题意. 17.（1）解：由A B =及已知，得()sin sin sin sin cos AA C A C A-=， 又sin 0A ≠，所以()sin cos sin A C A C -=，即sin cos cos sin cos sin A C A C A C -=， 所以sin cos 2cos sin A C A C =，又2C A π=-，则()()sin cos 22cos sin 2A A A A ππ-=-，所以-sin cos22cos sin2A A A A =，则()22sin 2cos 14cos sin A A A A --=， 所以-222cos 14cos A A +=，解得21cos 6A =， 故225sin 1cos 6A A =-=. （2）证明：由题意知，（sin sin cos cos sin )sin sin cos AB C B C B C A-=， 所以()sin sin cos sin sin cos cos sin A B C C B A B A =+， 则()2sin sin cos sin sin sin A B C C A B C =+=，由正弦定理，得2cos ab C c =，由余弦定理，得22222a b c ab c ab+-⨯=，整理，得2222223,3a b c a b c +=+=，故222a b c+为定值，得证. 18.解：（1）由频率分布表可知，10.150.250.300.100.20m =----=.这200份问卷得分的平均值估计为550.15650.25750.20850.30950.1074.5⨯+⨯+⨯+⨯+⨯=. （2）由分层抽样的方法可知，抽取的6人中，成绩在[)70,80内的有2人，分别记为12,A A ； 成绩在[)80,90内的有3人，分别记为123,,B B B ；成绩在[]90,100内的有1人，记为1C ，则从这6人中随机抽取3人的所有基本事件为{}{}{}{}{}121122123121112,,,,,,,,,,,,,,A A B A A B A A B A A C A B B ，{}{}{}{}{}{}{}{}113111123121131212213211,,,,,,,,,,,,,,,,,,,,,,,A B B A B C A B B A B C A B C A B B A B B A B C ，{}{}{}{}{}{}{}223221231123121131231,,,,,,,,,,,,,,,,,,,,A B B A B C A B C B B B B B C B B C B B C ，共20个，记这3人来自不同组为事件A ，其基本事件有{}{}{}{}{}111121*********,,,,,,,,,,,,,,A B C A B C A B C A B C A B C ，{}231,,A B C ，共6个，故这3人来自不同组的概率为()632010P A ==. 19.（1）证明：连结BD ，因为PD ⊥底面,ABCD BC ⊂平面ABCD ，所以PD BC ⊥.因为,4,AB AD AB AD ⊥==22218BD AD AB =+=.又BC CD ==222,BD CD BC BC CD =+⊥.又,PD CD D PD ⋂=⊂平面,PCD CD ⊂平面PCD ，所以BC ⊥平面PCD ， 又BC ⊂平面PBC ，故平面PCD ⊥平面PBC .（2）解：法一：由（1），得BD =所以()sin sin sin cos cos sin ABC ABD DBC ABD DBC ABD DBC ∠∠∠∠∠∠∠=+=+3==，则ABC 的面积为11sin 422ABCSAB BC ABC ∠=⨯=⨯⨯=故三棱锥P ABC -的体积为11433ABCP ABC V S PD -=⨯⨯=⨯=三校倠法二：因为,AB AD BC CD ⊥⊥，所以ABC ADC ∠∠π+=， 所以cos cos ABC ADC ∠∠=-.在ABC 与ADC 中， 由余弦定理得222222cos 2cos AC AB BC AB BC ABC AD CD AD CD ADC ∠∠=+-⋅⋅=+-⋅⋅，因此22224242ABC ABC ∠∠+-⨯⨯=++，解得cos ABC ∠=，所以sin ABC ∠=则ABC 的面积为11sin 422ABC S AB BC ABC ∠=⨯⋅=⨯⨯=，故三棱锥P ABC -的体积为114333ABC P ABC V S PD -=⨯⨯=⨯=三校倠. 20.解：（1）()()()()21e 331e 33x x f x x x x x =+-+=+-+'， 设()e 33x h x x =-+，则()e 3xh x '=-， 当(),ln3x ∞∈-时，()0h x '<，当()ln3,x ∞∈+时，()0h x '>，所以()h x 在(),ln3∞-上单调递减，在()ln3,∞+上单调递增，所以()()ln363ln30h x h =->，则e 330x x -+>，所以当(),1x ∞∈--时，()0f x '<，当()1,x ∞∈-+时，()0f x '>，故()f x 的单调递减区间为(),1∞--，单调递增区间为()1,∞-+.（2）当13x 时，()26f x ax x +恒成立，等价于e 3x a x x x --在1,3∞⎡⎫+⎪⎢⎣⎭上恒成立. 设()e 313x g x x x x x ⎛⎫=-- ⎪⎝⎭，则()()()22221e 1e 331x x x x x g x x x x---+=-+'=， 设()()211e 33x x x x x ϕ⎛⎫=--+ ⎪⎝⎭，则()()e 2x x x ϕ'=-， 当1,ln23x ⎛⎫∈ ⎪⎝⎭时，()0x ϕ'<，当()ln2,x ∞∈+时，()0h x '>， 所以()x ϕ在1,ln23⎛⎫ ⎪⎝⎭上单调递减，在()ln2,∞+上单调递增，则()()()()()22ln22ln21(ln2)32ln21(ln2)2ln22ln20x ϕϕ=--+>--+=->， 所以()0g x '>，则()g x 在1,3∞⎡⎫+⎪⎢⎣⎭上单调递增，故()g x 的最小值为12833g ⎛⎫= ⎪⎝⎭，所以3283e 3a-，所以实数a 的取值范围为283∞⎛⎤- ⎥⎝⎦. 21.解：（1）设E 的方程为221(0,0,)sx ty s t s t +=>>≠，由题意，1,1,2s s t =⎧⎪⎨+=⎪⎩解得11,2s t ==， 故E 的方程为2212y x +=. （2）由椭圆的对称性，不妨设F 为下焦点，则()0,1F -，所以()1,1AF =-， 因为0MN AF ⋅=，所以直线MN 的斜率为1，设直线MN 的方程为()()()11220,,,,y x m m M x y N x y =+≠，由221,2,y x y x m ⎧+=⎪⎨⎪=+⎩消去y 并整理得223220x mx m ++-=，则()()222Δ4432830m m m =-⨯⨯-=->，所以23m <且0m ≠.2121222,33m m x x x x -+=-=所以12MN x =-=== 原点O 到直线MN的距离为d =， 则MON的面积为)()223112223322MON m mS MN d +-=⨯⨯=⨯=⨯=， 当且仅当232m =，即2m =±时，MON 的面积最大， 显然2m =±满足23m <且0m ≠，所以MON22.解：（1）因为113123t t x ⎛⎫=+ ⎪⎝⎭，且22222211132,32433t t t t x y ⎛⎫=++=+- ⎪⎝⎭， 所以2244x y -=，则曲线C 的普通方程为()22114y x x -=. （2）由cos sin 10m ρθρθ+-=，化为直角坐标方程为10mx y +-=. 由2210,1,4mx y y x +-=⎧⎪⎨-=⎪⎩消去y 并整理得()224250m x mx -+-=. 则()2222240,Δ42040,20,450,4m m m m m m ⎧-≠⎪=+->⎪⎪⎨->⎪-⎪-⎪>-⎩解得2m <<， 故m的取值范围为(. 23.解：（1）()12,1,231,1,22112,,22x x f x x x x ⎧--<-⎪⎪⎪=-⎨⎪⎪+>⎪⎩当1x <-时，由1232x --，得714x -<-； 当112x -时，()3f x 恒成立； 当12x >时，由1232x +，得1524x <. 综上，()3f x 的解集为7544xx ⎧⎫-⎨⎬⎩⎭∣. （2）因为对任意1x ∈R ，都存在2x ∈R ，使得()()12f x g x =，所以(){}(){}yy f x y y g x =⊆=∣∣. 又()()()11311,22222f x x x x x g x x a x a =-++--+==-+--，等号都能取到，所以322a -，解得1722a ， 所以实数a 的取值范围是17,22⎡⎤⎢⎥⎣⎦.。

侧视图0.5俯视图1正视图10.5成都石室中学2023-2024年度上期高2024届入学考试数学试题（文）（总分：150分，时间：120分钟）第Ⅰ卷（共60分）一、选择题（本题共12道小题，每小题5分，共60分）1.已知集合{}14A x x =∈-≤<N ，{}2230B x x x =--<，则A B =I （）A ．{}1,2B ．{}0,1,2C ．{}1,2,3D ．{}0,1,2,32.若复数z 满足(13i)24i z ⋅+=-，则z =()A ．22B ．1C D ．23.函数23()e xx xf x -=的图象大致是()AB C D 4.已知实数,x y 满足()01x ya a a <<<，则下列关系式恒成立的是（）A ．221111x y >++B ．()()22ln 1ln 1x y +>+C ．sin sin x y>D ．33x y>5.若()0,0,lg lg lg a b a b a b >>+=+，则a b +的最小值为（）A.8B.6C.4D.26.已知命题:p 若22,ac bc >则a b >；命题:q 在ABC ∆中，sin sin A B =是A B =的必要不充分条件，则下列命题为真命题的是（）A ．p q ⌝∨ B.()p q ⌝∨ C.p q ∧ D.p q ∧⌝7.某四棱锥的三视图如图所示，则该四棱锥的体积是（）A ．14B.12C.1D.28.已知函数()sin(4)(0)f x A x ϕϕ=+<<π的图象与y 轴交点的坐标为，且图象关于直线24x π=-对称，将()f x 图象上所有点的纵坐标保持不变，横坐标变为原来的2倍，得到函数()g x 的图象，则()g x 在区间0,12π⎡⎤⎢⎥⎣⎦上的最大值为()A ．12B ．1C D ．29.已知ABC ∆中，若23A π=，2c =，ABC ∆的面积为32，D 为边BC 的中点，则AD 的长度是（）A.5714B.32C.1D.210.已知0.90.930.7,log 2a c ==，b=0.8，则a ，b ，c 的大小关系为（）A ．c a b <<B ．a c b <<C ．b a c <<D ．b c a<<11.已知圆2212316:()33C x y +-=过双曲线22222:1(0,0)x y C a b a b -=>>的左右焦点12,F F ,曲线1C 与曲线2C 在第一象限交点为M ，1212,MF MF ⋅=则双曲线2C 的离心率为（）A ．2B ．3C ．2D ．312.已知函数()114x xf x e e --=-+，若方程()4(0)f x kx k k =+->有三个不同的根1x ，2x ，3x ，则123x x x ++=（）A.4B.3C.2D.k第Ⅱ卷（共90分）二、填空题（本题共4道小题，每小题5分，共20分）13.已知倾斜角为α的直线l 与直线:230m x y -+=垂直，则cos 2α=.14.设x ，y 满足约束条件⎪⎩⎪⎨⎧≥-≥+≤--+0202222y x y x y x y x ，则y x z +=2的最大值是_________.15.直线01=--y x 与抛物线x y 42=交于,A B 两点，过线段AB 的中点作直线1-=x 的垂线，垂足为M ，则=⋅MB MA .16.已知三棱锥BCD A -中,2====AD BC CD AB ,t BD AC ==,当三棱锥BCD A -体积最大时,t 的值为.三、解答题（本题共6道小题，17题10分，其余各题12分，共70分）17．（本小题满分12分）已知数列{}n a 满足13a =，121n n a a n +=-+，数列{}n b 满足12b =，1n n n b b a n +=+-.（1）证明：{}n a n -是等比数列；（2）数列{}n c 满足()()111n n n n a nc b b +-=++，求数列{}n c 的前n 项的和n T .18．（本小题满分12分）如图，在四棱锥P -ABCD 中，四边形ABCD 为正方形，平面ADP ⊥底面ABCD ，AP =DP ，且AP ⊥DP ，设E ，F 分别为CP ，BD 的中点，2FP =．（1）求证：AP ⊥CP ；（2）求三棱锥P -ADE 的体积．已知某绿豆新品种发芽的适宜温度在6℃~22℃之间，一农学实验室研究人员为研究温度x （℃）与绿豆新品种发芽数y （颗）之间的关系，每组选取了成熟种子50颗，分别在对应的8℃~14℃的温度环境下进行实验，得到如下散点图：其中24y =,71()(70i i i x x y y =--=∑，721()=176i i y y =-∑．（1）运用相关系数进行分析说明，是否可以用线性回归模型拟合y 与x 的关系？（2）若求出 y 关于 x 的线性回归方程y bx a =+$$$，并预测在19℃的温度下，种子的发芽的颗数．参考公式：相关系数()()nii xx y y r --=∑y bx a =+$$$，其中121()(()nii i nii xx y y bxx ==--=-∑∑ ，a y bx =-$$8.77≈．20．（本小题满分12分）已知椭圆1C ：22221x y a b+=（0a b >>）左、右焦点分别为1F ,2F ，且2F 为抛物线22:8C y x=的焦点，P 为椭圆1C 上一点.（1）求椭圆1C 的方程；（2）已知A ，B 为椭圆1C 上不同两点，且都在x 轴上方，满足12F A F B λ=.（ⅰ）若3λ=，求直线1F A 的斜率；（ⅱ）若直线1F A 与抛物线2y x =无交点，求四边形12F F BA 面积的取值范围.设()ln f x x =．（1）证明：()y f x =的图象与直线xy e=-有且只有一个横坐标为α的公共点，且1(,1)e α∈；（2）求所有的实数k ，使得直线y kx =与函数2()y f x =的图象相切；（3）设2,,((,)a b c eα∈+∞（其中α由（1）给出），且3a b c ++=，()ln 2g x x =+，求g 2(a )+g 2(b )+g 2(c )的最大值．22．（本小题满分10分）在直角坐标系中，直线的方程为，曲线的参数方程为（为参数），点，分别在直线和曲线上运动，的最小值为.(1)求的值；(2)以坐标原点为极点，轴正半轴为极轴建立极坐标系，射线与曲线交于不同的两点与直线交于点，若，求的值.成都石室中学2023-2024年度上期高2024届入学考试数学试题（文）参考答案一、选择题题号123456789101112答案BCADCDACBACB二、填空题13.35-;14.3+15.0;16.433.三、解答题17．解：（1）121n n a a n +=-+()()112n n a n a n +∴-+=-，又因为112a -=，所以{}n a n -是首项为2，公比为2的等比数列.．．．．．．．．．．．．．5分（2）()11122n nn a n a --=-⋅=1n n n b b a n +=+-12nn n b b +∴-=()()()()121112*********n n n n n n n n b b b b b b b b n -----∴=-+-+-+=++++=≥ 12b =满足上式.2nn b ∴=()()()()1112111121212121n n n n n n n n n a n c b b +++-===-++++++12231111111111212121212121321n n n n T ++⎛⎫⎛⎫⎛⎫∴=-+-++-=- ⎪ ⎪ ⎪+++++++⎝⎭⎝⎭⎝⎭ .．．．．．．．．．．．．．12分18．解：（1）∵ABCD 是正方形，∴AD ⊥CD ．（1分）∵侧面PAD ⊥底面ABCD ，侧面PAD 底面ABCD =AD ，AD ⊂平面PAD ，∴CD ⊥平面PAD ，（3分）∴CD ⊥AP ．又AP ⊥DP ，CD ∩DP =D ，∴AP ⊥平面PCD ，（5分）∴PA PC ⊥．（6分）（2）∵四边形ABCD 为正方形，连接AC ，则AC ∩BD =F ，F 为AC 中点．∵E 为PC 中点，∴在△ACP 中，EF PA ∥．∵PA ⊂平面ADP ，EF ⊄平面ADP ，∴EF 平面ADP ．∴E 到面ADP 的距离等于F 到面ADP 的距离．（8分）由（1）知，PA PC ⊥，∴12PF AC ==AC=，∴2AB AD ==,PA PD ==（9分）（法一）取AD 中点M ，连接AC ，MF ，则MF ∥CD ，又CD ⊥平面ADP ，∴MF ⊥平面ADP ．∴111113323P ADE E PAD F PAD PAD V V V MF ---∆===⋅=⨯=．（12分）（法二）取AD 中点M ，连接AC ，MF ，则PM ⊥AD ．∵侧面PAD ⊥底面ABCD ，侧面PAD 底面ABCD =AD ，PM ⊂平面PAD ，∴PM ⊥底面ABCD ，112PM AD ==．∴11111213323P ADE E PAD F PAD P ADF ADF V V V V S PM ----∆====⋅=⨯⨯⨯⨯=．（12分）19．解：（1）根据题意，得()1891011121314117x =++++++=．（1分）()()()()()()()()2222227122811+911+1011+1111+1211+1311+1411=28i i x x =-------=-∑（2分）70.16．（3分）因而相关系数()()7700.99870.16iix x y y r --==≈∑．（5分）由于0.998r ≈很接近1，∴可以用线性回归方程模型拟合y 与x 的关系．（6分）（2）()()()7172178ˆ0522i ii ii x x yy bx x ==--===-∑∑，（8分）5724112ˆ2a=-⨯=-，（9分）∴ y 关于 x的回归方程为5722ˆy x =-．（11分）若19x =，则5719442ˆ2y=⨯-=颗．∴在19℃的温度下，种子的发芽颗数为44．（12分）20．解：（1）依题意得2c =，则1(2,0)F -，2(2,0)F .于是12a PF =2PF +=，从而a =又222a b c =+，解得2b =所以椭圆1C 的方程为22184x y +=.．．．．．．．．．．．．．3分（2）如图，设1F A 直线交椭圆于另一点'B ，2F B 直线交椭圆于另一点A'，由12F A F B λ=，故12//F A F B ，由椭圆对称性，2112',A'BF B F AF F ==，且四边形''ABA B 为平行四边形.．．．．．．．．．．．．．5分○1由题意直线'AB 的斜率不为0，设直线'AB ：2x ty =-，由22228x ty x y =-⎧⎨+=⎩，消去x 整理得()222440t y ty +--=，设()11,A x y ，()22',B x y ，则12242t y y t +=+，12242y y t =-+，由12111233'3F A F B F A F B y y =⇒=-⇒=-（*）带入上式，解得：122262,22t ty y t t -==++故2222124,0(),1(2)2t t t t t -=->∴=++由图Q ，故1F A 的斜率为1.．．．．．．．．．．．．．8分○2由22x ty y x=-⎧⎨=⎩，消去x 整理得220y ty -+=，由()280t ∆=--<得28t <.所以12'AB y =-=)2212t t +=+，'AB 与'BA 间的距离d =2F 到'AB 的距离），故1212AF F BAB A B S S ''==)221122t t +⋅+28212t =+，[)1,3s =∈，则1222AF F BS t=+211s s s==++5⎛∈ ⎝，所以四边形12AFF B的面积的取值范围为5⎛⎝⎦.．．．．．．．．．．．．．12分21．解：（1）考虑函数()ln xu x x e =+，易知()u x 在(0,1)上单调递增，且(1)0u >，1()0u e<．因此有且只有1(,1)e α∈使得()0u α=，即()y f x =的图象与直线x y e=-有且只有一个公共点，且该公共点的横坐标为α．…………3分（2）22ln [()]xf x x'=．设200(,ln )P x x 是2()y f x =的图象上一点，则该点处的切线为200002ln ln ()x y x x x x -=-，整理得200002ln 2ln ln x y x x x x =-+．令2002ln ln 0x x -+=，解得01x =或20x e =．因此0y =与24y x e=与函数2()y f x =的图象相切．因此所求实数k 的值为0或24e ．…………7分（3）设224()ln h x x x e =-，则22ln 4()x h x x e '=-．设ln ()x x x ϕ=，则21ln ()xx xϕ-'=．当2x e α<<时，()0x ϕ'>；当x e >时，()0x ϕ'<．因此()x ϕ在2(,)e α上单调递增，在(,)e +∞上单调递减．从而()h x '在2(,)e α上单调递增，(,)e +∞上单调递减．注意到2()0h e '=，故当2e x e <<时()0h x '>，当2x e >时()0h x '<，因此()h x 在2(,)e e 上单调递减，在2(,)e +∞上单调递增．所以当[,)x e ∈+∞时，2()()0h x h e ≤=．另一方面，注意到24(1)0h e '=-<，故必然存在0(1,)x e ∈，使得0()0h x '=，且当20x x α<<时()0h x '<，当0x x e <<时()0h x '>．因此()h x 在20(,)x α上单调递减，在0(,)x e 上单调递增．显然2()()0h e h e <=，而22222422()ln (2ln )(2ln )0h e e eααααα=-=+-=．因此当2(,)x e α∈时，()0h x <．综上可知当2x α>时()0h x ≤，即224ln x x e≤，当且仅当2x e =时等号成立．由于222()ln ()g x e x =，故当22e x α>，即2()x e α>时，2224()()4g x e x x e<⋅=，当且仅当22e x e =，即1x =时等号成立．因此222()()()44412g a g b g c a b c ++≤++=，当且仅当1a b c ===时等号成立．因此222322……5分（2）曲线:2cos C ρθ=，直线:(cos sin )4l ρθθ+=，分别代入θα=，得2cos A ρα=，4sin cos B ραα=+，由||||OA AB =知2B A ρρ=，即44cos sin cos ααα=+，2sin cos cos 1ααα∴+=即π2sin(2)42α+=，故π3π244α+=即π4α=.……10分。

高三数学注意事项：1.答题前，考生务必将自已的姓名，为生号，考场号，座位号填写在答题卡上.2.回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题号的答案标号涂黑.如需改动，用橡皮擦干净后，再选涂其他答案标号.回答非选择题时，将答案写在答题卡上.写在本试卷上无效.3.考试结束后，将本试卷和答题卡一并交回.4.本试卷主要考试内容：高考全部内容.一､选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.已知集合{}1,0,1,2,{|11}A B x x =-=->，则A B Ç=（）A.{}0B.{}1-C.{}1,0,1-D.{}1,0,1,2-2.()()32i 22i +-=（）A.102i -+B.102i-- C.102i+ D.102i -3.已知()2xf x =，则()3f =（）A.8B.9C.2log 3D.3log 24.国家统计局发布的2018年至2022年我国居民消费水平情况如图所示，则下列说法正确的是（）（居民消费水平：´´农村居民消费水平农村人口数+城镇居民消费水平城镇人口数农村人口数+城镇人口数）A.2018年至2022年我国居民消费水平逐年提高B.2018年至2022年我国城镇居民消费水平逐年提高C.2018年至2022年我国居民消费水平数据的60%分位数为27504元D.2022年我国城镇人口数比农村人口数的1.5倍还要多5.已知ππsin cos sin 44a a a æöæö-+-=ç÷ç÷èøèø，则πtan 4a æö-=ç÷èø（）A.0B.1C.-1 6.某班级举行“变废为宝”手工活动，某学生用扇形纸壳裁成扇环（如图1）后，制成了简易笔筒（如图2）的侧面，在它的轨截面ABCD 中，10cm,15cm AB AD CD ===，则原扇形纸壳中扇形的圆心角为（）A.π3B.π2C.π4D.π67.过原点O 的直线:l y kx =与圆22:66160M x x y y -+-+=交于,A B 两点，且OA AB =，则k =（）A.1B.2C.128.已知函数()()sin (0)f x x w j w =+>，若任意(),f x j ÎR 在π0,2æöç÷èø上有零点，则w 的取值范围为（）A.()0,¥+B.()1,¥+C.()2,¥+D.()3,¥+二､多选题：本题共3小题，每小题6分，共18分.在每小题给出的选项中，有多项符合题目要求.全部选对的得6分，部分选对的得部分分，有选错的得0分.9.已知双曲线2222:1(0,0)x y C a b a b-=>>的左､右焦点分别为12,,F F O 为坐标原点，直线y b =与双曲线C的渐近线交于点,A B （A 在第二象限，B 在第一象限），下列结论正确的是（）A.12BF BF ^B.2BF ∥AOC.若OAB V 的面积为2，则双曲线C 的焦距的最小值为4D.若OAB V 的面积为2，则双曲线C 的焦距的最小值为810.如图，三角形数阵由一个等差数列2,5,8,11,14,L 排列而成，按照此规律，下列结论正确的是（）A.数阵中前7行所有数的和为1190B.数阵中第8行从左至右的第4个数是101C.数阵中第10行的第1个数是137D.数阵中第10行从左至右的第4个数是14611.已知定义在R 上的函数()f x 满足()()()()f x f x f x y f xy éù--=ëû，当()(),00,x ¥¥Î-È+，时，()0f x ¹.下列结论正确的是（ ）A.1122f æö=ç÷èø B.()101f =C.()f x 是奇函数D.()f x 在R 上单调递增三､填空题：本题共3小题，每小题5分，共15分.12.已知抛物线2:2(0)C y px p =>的焦点为F ，点,4p P a æöç÷èø在抛物线C 上，且3PF =，则p =__________.13.甲､乙两位同学进行羽毛球比赛，约定赛制如下：累计赢2局者胜，分出胜负即停止比赛.已知甲每局赢的概率为35，每局比赛的结果相互独立.本次比赛到第3局才分出胜负的概率为__________，本次比赛甲获胜的概率为__________.14.如图，将正四棱柱1111ABCD A B C D -斜立在平面a 上，顶点1C 在平面a 内，1AC ^平面1,26AA AB a ==.点P 在平面a 内，且1PC =若将该正四棱柱绕1AC 旋转，PC 的最大值为__________.四､解答题：本题共5小题，共77分.解答应写出文字说明､证明过程或演算步骤.15.（13分）已知正项等比数列{}n a 满足121316,a a a a a +==.（1）求{}n a 的通项公式；（2）记{}n a 的前n 项中最大值为n M ，最小值为n m （规定：111M m a ==），令2n nn M m b +=，求数列{}n b 的前n 项和n S .16.（15分）将3个数字1，2，3随机填入如下99个空格中，每个空格中最多填一个数字，且填入的3个数字从左到右依次变大.（1）求数字2填在第2个空格中的概率；（2）记数字2填在第x 个空格中的概率为()P x ，求()P x 的最大值.17.（15分）如图，在四棱锥P ABCD -中，四边形ABCD 是菱形，,,PA AC BD PC PA AB ^^=.（1）证明：PA ^平面ABCD .（2）若4,60PC PE ABC Ð==o uuu r uuu r，求二面角A BD E --的余弦值.18.（17分）已知椭圆C 的方程为22221(0)x y a b a b+=>>，右焦点为()1,0F ，且离心率为12（1）求椭圆C 的方程；（2）过点F 的直线l 与椭圆C 交于,A B 两点，证明，圆22325416x y æö-+=ç÷èø恒与以弦AB 为直径的圆相切.19.（17分）已知函数()f x =.（1）若曲线()y f x =在点()(),a f a 处的切线过点()4,2，求a 的值；（2）若()1ex f x a -…恒成立，求a 的取值范围.高三数学参考答案1.B ()(){},02,,1B A B ¥¥=-È+Ç=-.2.D()()232i 22i 66i 4i 4i 102i +-=-+-=-.3.C 令23x =，可得2log 3x =，则()23log 3f =.4.D 2019年的居民消费水平比2020年的居民消费水平高，A 错误.2019年的城镇居民消费水平比2020年的城镇居民消费水平高，B 错误.2018年至2022年我国居民消费水平数据从小到大排序为25245,27439,27504,31013,31718,560%3,2018´=年至2022年我国居民消费水平数据的60%分位数为275043101329258.52+=元，C 错误.设我国农村人口数为x ，城镇人口数为y ，则195303828931718x y x y +=+，化简得12188365712y x =>，所以2022年我国城镇人口数比农村人口数的1.5倍还要多，D 正确.5.C 因为ππsin cos 44a a a æöæö-+-=ç÷ç÷èøèøsin a a =，则sin 0a =，即π,k k a =ÎZ ，所以ππtan tan π144k a æöæö-=-=-ç÷ç÷èøèø.6.B 延长,CB DA 交于点O ，设圆台上､下个底面的闪心分别为21,O O .连接1OO ，设21,,OB x O B r O C R ===.因为21OO B OO C V V ∽，所以r OBR OC=，则20cm x =.设所求圆心角为q ，则2πx r q =，所以2ππ2r x q ==.7.A 圆22:66160M x x y y -+-+=，即圆22:(3)(3)2M x y -+-=，圆心()3,3M 到直线l 的距离为,d AB 的中点为C .因为OA AB =，所以3OC AC =.因为OM ==，所以OC ==.又因为AC ==，解得0d =，所以直线l 经过圆心()3,3M ，所以30130k -==-.8.C 令t x w j =+，由题意可得sin 0t =在π,2w j j æö+ç÷èø上有解.因为sin 0t =在[],a b 内有解的最短区间长度为πb a -=.所以ππ2wj j +->，解得2w >.9.AC12OB c OF OF ===，点B 在以O 为圆心，1OF 为半径的圆上，所以12BF BF ^，A 正确.直线2BF 的斜率为b c a --，直线AO 的斜率为,b b a c a---与b a -不一定相等，所以直线2BF 与直线AO 不一定平行，B 错误.OAB V 的面积为1222a b ab ××==，双曲线C 的焦距为24c ===，当且仅当a b ==时，等号成立，所以双曲线C 的焦距的最小值为4,C 正确，D 错误.10.ACD 设等差数列2,5,8,11,14,L 的通项公式为31n b n =-.数阵中前7行共123728++++=L 个数，数阵中前7行所有数的和为2827322811902´´´+=，A 正确.令31101n b n =-=，解得34n =，前7行共28个数，第8行有8个数，所以101是数阵中第8行从左至右的第6个数，B 错误.记每一行的第1个数组成数列{}n a ，则()121324312,3,632,933,,31n n a a a a a a a a a n -=-=-==´-==´-=´-L ，累加得()()131312312n n n a a n --=´++++-=L ，所以210334,1372n n n a a -+==，C 正确.数阵中第10行从左至右的第4个数是()137413146+-´=，D 正确.11.ACD 令0x y ==，可得()00f =.令1x y ==，可得()()2[1]1f f =.因为当0x >时，()0f x ¹，所以()11f =.令x y =，可得()()22[]0f x f x =….因为20x …，所以当0x …时，()0f x ….又因为当0x >时，()0f x ¹，所以当0x >时，()0f x >.令1y =，可得()()()()1f x f x f x f x éù--=ëû，①所以()()()()11,11f x f x f x f x --=+-=，两式相加可得()()112f x f x +--=.令1y =-，可得()()()()1f x f x f x f x éù-+=-ëû.②①-②可得()()()()()11f x f x f x f x f x éù+--=--ëû，化简可得()()f x f x =--，所以()f x 是奇函数，C 正确.由()()11f x f x --=，可得()()()()()()()2112,3213,4314,,1010f f f f f f f =+==+==+==L ，B 错误.由()()()()11,,fx f x fx f x ì+-=ïí=--ïî可得111,2211,22f f ff ìæöæö--=ç÷ç÷ïïèøèøíæöæöï=--ç÷ç÷ïèøèøî解得11,A 22f æö=ç÷èø正确.令112,x x y x x ==-，可得()()()()()112121f x x x f x f x f x --=.令210x x <<，则()121120,0x x x x x ->->.因为当0x >时，()0f x >，所以()()()11120,0f x f x x x >->，所以()()()()()1121210f x x x f x f x f x --=>，即()()12f x f x >，所以()f x 在()0,¥+上单调递增.因为()f x 为奇函数，所以()f x 在R 上单调递增，D 正确.12.4 342p pPF =+=，解得4p =.13.1225；81125（本题第一空2分，第二空3分）到第3局才分出胜负，则前两局甲､乙各赢一局，其概率为123212C 5525´´=.若甲获胜，分2种情况：①甲连赢2局，其概率为3395525´=，②前两局甲､乙各赢一局，第三局甲赢，其概率为1232336C 555125´´´=.故甲获胜的概率为9368125125125+=.14. 过点C 作1CE AC ^，垂足为E ，连接AC .易得CE ∥平面a ，所以点C 到平面a的距离为11.C E AC AC ==1CE C E =====过点C 作CC ¢^平面a ，垂足为C ¢（图略）.当1,,C C P ¢三点共线，且11C P C C C P +¢=¢时，PC==.15.解：（1）设{}n a 的公比为q ，则11231116,,a a q a a q a q +=ìí×=î解得12a q ==或3q =-（舍去）.所以{}n a 的通项公式为2nn a =.（2）因为{}n a 是递增数列，所以2,2nn n M m ==，1222122n n n n n M m b -++===+.122112nn n S n n -=-=+--.16.解：（1）数字2填在第2个空格中的概率为197399C 1C 1617=.（2）由题意可得298x ……，且x +ÎN .()()()11199339999199C C C C x xx x P x ----==.当50x =时，()P x 取得最大值，最大值为23994949C 3201=.17.（1）证明：记AC BD O Ç=.因为四边形ABCD 是菱形，所以BD AC ^.因为,BD PC PC ^Ì平面,PAC AC Ì平面PAC .且AC PC C Ç=，所以BD ^平面PAC .因为PA Ì平面PAC ，所以BD PA ^.因为,PA AC AC ^Ì平面,,ABCD BD Ì平面ABCD ，且AC BD O Ç=，所以PA ^平面ABCD .（2）解：以O 为坐标原点，分别以,OC OD uuu r uuu r的方向为,x y 轴的正方向，建立如图所示的空间直角坐标系.设4AB =，则()()()()0,,0,1,0,3,1,,(0B D E BE BD -×-=-=uuu r uuu r，.设平面BDE 的法向量为(),,m x yz =r，则30,m BD m BE x z ì×=ïí×=-++=ïîuuu r r uuu r r 令3x =，得()3,0,1m =r .平面ABD 的一个法向量为()0,0,1n =r.cos ,n =r 易得二面角A BD E --为锐角，故二面角A BD E --.18.（1）解：由题意得椭圆C 的半焦距1c =，且12c e a ==，所以2a =.又因为2223b a c =-=，所以椭圆C 的方程为22143x y +==.（2）证明：当直线l 的斜率为0时，直线l 的方程为0x =此时AB 为椭圆C 的长轴，以弦AB 为直径的圆的方程为224x y +=，该圆的半径为2.圆22325416x y æö-+=ç÷èø的半径为54，两圆的圆心距为53244-=.满足圆22325416x y æö-+=ç÷èø恒与以弦AB 为直径的圆相切.当直线l 的斜率不为0时，设直线l 的方程为()()11221,,,,,x ty A x y B x y AB =+的中点为()00,M x y .联立221,1,43x ty x y =+ìïí+=ïî得()2234690t y ty ++-=，所以12122269,3434t y y y y t t +=-=-++，120002234,123434y y t y x ty t t +==-=+=++.()2212134t AB t +==+.记圆22325416x y æö-+=ç÷èø的圆心为3,04N æöç÷èø，()2294434t t +=+.()()()()2222226153419452344434434t t t AB MN t t t +++-=-==+++.满足圆22325416x y æö-+=ç÷èø恒与以弦AB 为直径的圆相切.综上，圆22325416x y æö-+=ç÷èø恒与以弦AB 为直径的圆相切.19.解：（1）()()()f a f x f a =¢¢==曲线()y f x =在点()(),a f a处的切线方程为)y x a -=-.因为该场线过点()4,2，所以)24a -=-，解得4a =.（2）因为()1e x f x a -=，所以0a >，且2a x >.两边平方可得222e 2x a x a --….令函数()()()222222e2,2e 12x x a g x a x a x g x a --æö=-+>=¢-ç÷èø.令函数()()222222e1,2e 0x x h x a h x a --=-=>¢，所以()h x 是增函数.令()()2222e 10x g x a -=-=¢，得1ln x a =-.下面比较1ln a -与2a 的大小.令函数()()()21ln ,0,22a a u a a u a u a a ¢+=--=-<是减函数.因为()()110,2ln202u u =>=-<，所以存在()01,2a Î，使得当()00,a a Î时，()0u a >，即1ln 2a a ->.当[)0,a a ¥Î+时，()0u a …，即1ln 2a a -….当()00,a a Î时，当,1ln 2a x a æöÎ-ç÷èø时，()0h x <，即()0g x ¢<；当()1ln ,x a ¥Î-+时，()0h x >，即()0g x ¢>.所以()g x 在,1ln 2a a æö-ç÷èø上单调递减，在()1ln ,a ¥-+上单调递增.()()22ln min ()1ln e 21ln 2ln 1a g x g a a a a a a -=-=--+=+-.令函数()()22ln 1,10v a a a v a a=+-=+>¢，所以()v a 是增函数.由题意可得min ()2ln 10g x a a =+-…，又因为()10v =，所以01a a <….当[)0,a a ¥Î+时，min ()02a g x g æö=>ç÷èø，符合题意.综上，a 的取值范围为[)1,¥+.。