下载文档原格式
多面体体积面积计算公式大全
以下是常见多面体的体积和面积计算公式大全：
1. 立方体
体积：V = l × w × h
表面积：A = 6l^2
2. 正方体
体积：V = s^3
表面积：A = 6s^2
3. 三棱柱
体积：V = Bh，其中B为底面积，h为高
表面积：A = 2B + Ph，其中P为底边周长
4. 四棱锥
体积：V = 1/3Bh，其中B为底面积，h为高
表面积：A = B + 1/2Pl，其中P为底边周长，l为斜高5. 圆柱
体积：V = πr^2h，其中r为底面半径，h为高
表面积：A = 2πr^2 + 2πrh
6. 圆锥
体积：V = 1/3πr^2h，其中r为底面半径，h为高
表面积：A = πr^2 + πrl，其中l为斜高
7. 球体
体积：V = 4/3πr^3，其中r为半径
表面积：A = 4πr^2
8. 正多边形棱柱
体积：V = (1/4)na^2h/tan(π/n)，其中n为边数，a为边长，h为高
表面积：A = nah + 2B，其中B为底面积
9. 正多边形棱锥
体积：V = (1/3)nAa/2h，其中n为边数，a为边长，h为高，A 为底面积
表面积：A = nA + 1/2Pl，其中P为底边周长
注意：以上公式仅限于各部分均为规则多边形的情况。
对于不规则多边形或不均匀的物体，需要采用更复杂的方法进行计算。
多面体体积和面积公式多面体是指有多个面的立体图形，常见的多面体有立方体、正四面体、正六面体、正八面体、正十二面体等。
每种多面体都有其独特的体积和面积公式。
一、立方体：立方体是一个长宽高相等的六面体。
它的体积公式为：V=边长^3它的表面积公式为：A=6*边长^2二、正四面体：正四面体是一个底面为等边三角形，且其余三个面均为等边三角形的四面体。
它的体积公式为：V=√2/12*边长^3它的表面积公式为：A=√3*边长^2三、正六面体：正六面体是一个六个面均为正方形的立体图形。
它的体积公式为：V=边长^3它的表面积公式为：A=6*边长^2四、正八面体：正八面体是一个八个面均为等边三角形的立体图形。
它的体积公式为：V=√2*边长^3它的表面积公式为：A=2*√3*边长^2五、正十二面体：正十二面体是一个十二个面均为正五边形的立体图形。
它的体积公式为：V=(3+√5)/12*边长^3它的表面积公式为：A=3*√25+10*√3*边长^2以上是常见多面体的体积和面积公式，可以根据不同的多面体类型进行使用。
此外还有许多其他多面体，每个多面体都有其一系列的特性和公式，需要具体问题具体分析。
除了常见多面体的公式外，还有一些统一的多面体公式，适用于凸多面体。
1.多面体的体积公式：对于凸多面体，可以利用封闭曲面积分的方法求解其体积。
V=1/3*Σ(S_i*h_i)其中，S_i表示多面体第i个面的面积，h_i表示从多面体重心到第i个面的垂直高度，Σ表示求和。
2.多面体的表面积公式：对于凸多面体，可以利用表面积的计算公式求解其表面积。
多面体表面积公式可以表示为：A=1/2*Σ(S_i*l_i)其中，S_i表示多面体第i个面的面积，l_i表示第i个面的边长，Σ表示求和。
综上所述，多面体的体积和面积公式可以根据具体的多面体类型进行选择，对于凸多面体还可以使用统一的公式来计算。
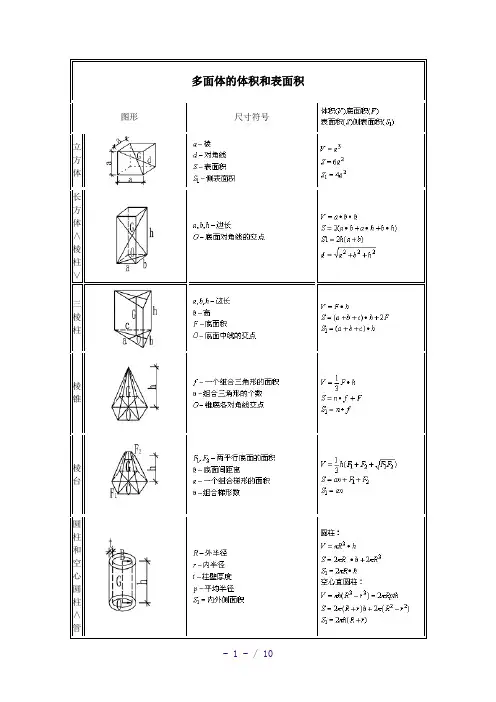
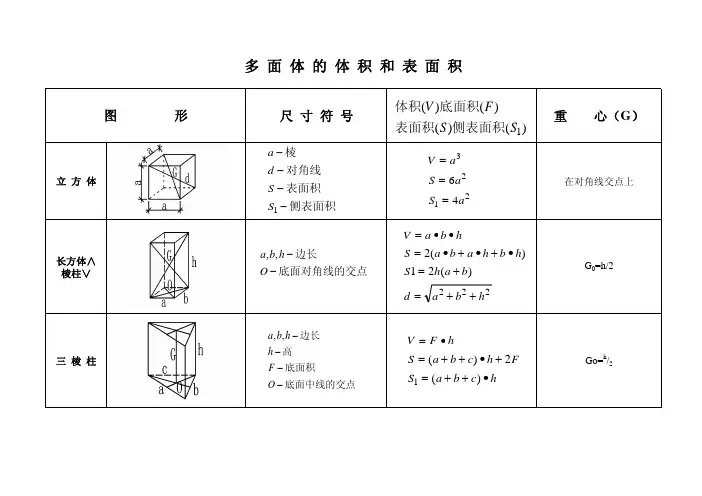
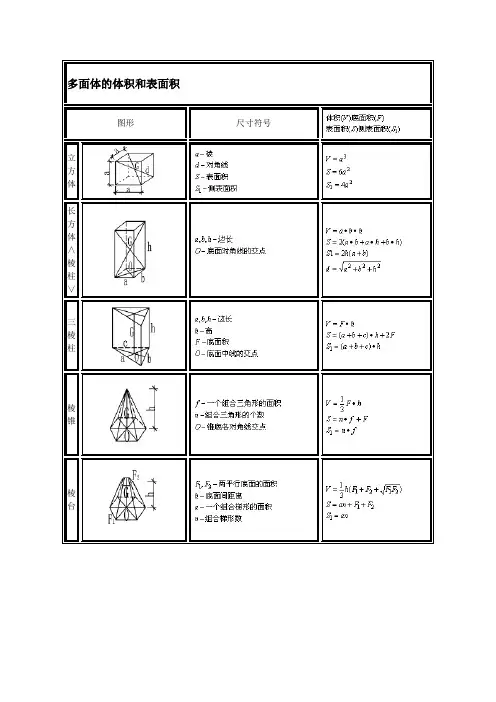
多面体的体积和表面积图形尺寸符号
立
方
体
长
方
体
∧
棱
柱
∨
三
棱
柱
棱
锥
棱
台
圆
柱
和
空
心
圆
柱
∧
管
斜线直圆柱
直圆锥
圆台
球
球扇形∧球楔∨
球缺
圆环体∧胎∨
球
带
体
桶
形
椭
a,b,c-半轴
球
体
交
叉
圆
柱
体
梯
形
体
常用图形求面积公式
图形尺寸符号面积（F）表面积（S）
正方形
长方形
三角形
平行四边形
任意四边形
正多边形
菱形
梯形
圆形
椭
a·b-主轴F= (π/4) a·b
圆
形
扇
形
弓
形
圆
环
部
分
圆
环
新
月
形
L d/102d/10 3d/10 4d/105d/10 6d/10 7d/10 P 0.400.79 1.18 1.56 1.91 2.25 2.55
抛物线形
等多边形
（注：文档可能无法思考全面，请浏览后下载，供参考。
可复制、编制，期待你的好评与关注）。
