各种多面体体积、面积计算公式大全(施工员必备)

多面体公式计算大全
1.正方体：
-面数：6面
-边数：12条
-顶点数：8个
-表面积：每个面都是边长的平方，总表面积等于6倍的边长平方。

-体积：边长的立方。

2.正四面体：
-面数：4面
-边数：6条
-顶点数：4个
-表面积：底面积加上3个侧面积，底面积是边长的平方再乘以根号3除以4
-体积：边长的立方再乘以根号2除以12
3.正六面体（立方体）：
-面数：6面
-边数：12条
-顶点数：8个
-表面积：每个面都是边长的平方，总表面积等于6倍的边长平方。

-体积：边长的立方。

4.正八面体：
-面数：8面
-边数：12条
-顶点数：6个
-表面积：底面积加上6个侧面积，底面积是边长的平方再乘以根号3
-体积：边长的立方再乘以根号2除以3
5.正十二面体：
-面数：12面
-边数：30条
-顶点数：20个
-表面积：每个面都是边长的平方再乘以根号3除以4，总表面积等于12倍的边长平方乘以根号3
-体积：边长的立方再乘以根号2除以3
6.正二十面体：
-面数：20面
-边数：30条
-顶点数：12个
-表面积：每个面都是边长的平方再乘以根号3除以4，总表面积等于20倍的边长平方乘以根号3
-体积：边长的立方再乘以根号2除以3
除了以上常见的多面体，还有其他更复杂形状的多面体需要使用更复杂的计算公式。

在实际计算中，我们也可以使用符号计算软件、几何计算器等工具进行更准确和复杂的计算。

希望以上多面体的计算公式可以对您有所帮助。

多面体的体积和表面积y = F*hE - (c +b +u)・ A + ；F E\=g +&+f ) • #2I 評耳+马+应） £ =㈱H ■巧十尽5j = cm图形 尺寸符号体积（町唐面积（F ） 表輪⑸佩俵翻斶）口-楼 止-寰面积侧表面积r = a 3£=討 商=4a a长 方 体 A 棱 柱 V龟以1边按。

-尿面对角线的交点f 二2仗*方+Q •丙+B*月) 51 = 2^+^)棱 锥棱 厶务马-两平行底面的面积 h■麻面间距盅 位-Y 爼台棉殛的面科 皿-殂合梯幣埶口,冊-述长b ■高F -底直积口 L 底面中钱的敦f-一①组舍三请形的面枳腥-组合三轴我的个数0-镀底各刑第钱交直棱 柱£ = 2?rji •/] 4-2JC JE^圆 柱 和 空 心、 圆 柱A管V斜 线 直 圆 柱球扇 形A球楔覇=时偽十址)球V圆 台”克径BS ：r -鹿面半径用—高 J 世錢长「-碌半径 用-弓形底圆直径 h-弓托高艮-外芈径 一内半径 !-柱壘厚愛 卩-平均半轻 场=内汁侧面积R?■-底面半径 h -奩廿胪+胖二曲』r= -^^ = 20^3*3屈=吃（联+町=157班価+百U岛-棗才'高度 阳-最丸高度r-底面半孫£■圖坯+岛）斗寸—（1+—i —）V ■—宀------- 0.5236^3 6 S u JrtT 2 - mF八争(C®Sj = nf(J?+r)百=$1十试沪十宀"4学§= 2n-R * h 空心苴圆柱■F =锁/—田=2碑朽£=2机卫4町；!+2代皿一以）$ =2囲只+H。

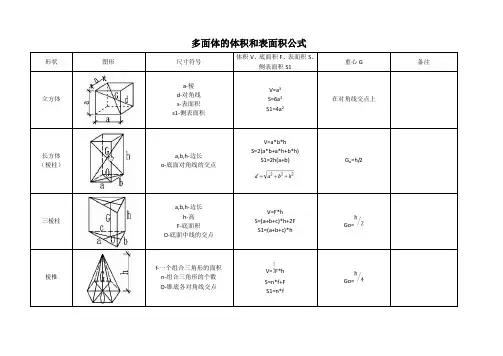
多面体的体积和表面积公式形状图形尺寸符号体积V、底面积F、表面积S、侧表面积S1重心G 备注立方体a-棱d-对角线s-表面积s1-侧表面积V=a3S=6a2S1=4a2在对角线交点上长方体（棱柱）a,b,h-边长o-底面对角线的交点V=a*b*hS=2(a*b+a*h+b*h)S1=2h(a+b) G o=h/2三棱柱a,b,h-边长h-高F-底面积O-底面中线的交点V=F*hS=(a+b+c)*h+2FS1=(a+b+c)*hGo=棱椎f-一个组合三角形的面积n-组合三角形的个数O-锥底各对角线交点V=F*hS=n*f+FS1=n*fGo=多面体的体积和表面积公式形状图形尺寸符号体积V、底面积F、表面积S、侧表面积S1重心G 备注棱台F1,F2-两平行底面的面积h-底面间距离a-一个组合梯形的面积n-组合梯形数V=h(F1+F2+S=an+F1+F2S1=an圆柱和空心圆柱（管）R-外半径r-内半径t-柱壁厚度P-平均半径S1=内外侧面积圆柱：V=πR2*hS=2πR*h+2πR2S1=2πR*h空心直圆柱：V=πh(R2-r2)=2πRpthS=2π(R+r)h+2π(R2-r2)S1=2πh(R+r)Go=h/2斜线直圆柱r-底面半径h- 高l-母线长V=πr2hS1=πr=πrll=S=S1+πr2Go=h/4直圆椎h1-最小高度h2-最大高度r-底面半径V=πr2*S=πr(h1+h2)+πr2*(1+)S1=πr(h1+h2)多面体的体积和表面积公式形状图形尺寸符号体积V、底面积F、表面积S、侧表面积S1重心G 备注圆台R，r-底面半径h-高l-母线V=*(R2+R2+Rr)S1=πl(R+r)l=S=S1+π(R2+r2)球r-半径d-直径V=πr3=πd3/6=0.5236d3S=4πr2=πd2在球心上球扇形（球楔）r-球半径d-弓形底圆直径h –弓形高V=πr2h=2.0944r2hS=(4h+d)=1.57r(4h+d)Go=3/4(r-h/2)球缺h- 球缺的高r- 球缺半径d-平切圆直径S曲=曲面面积S-球缺表面积V=πh2(r-)S曲=2πrh=π(d2/4+h2)S=πh(4r-h)d2=4h(2r-h)Go=3(2r-h)2/4(3r-h)多面体的体积和表面积公式形状图形尺寸符号体积V、底面积F、表面积S、侧表面积S1重心G 备注圆环体（胎）R-圆球体平均半径D-圆环体平均半径d-圆环体截面直径r-圆环体截面半径V=2πr2R*r2=2Dd2S=4πr2Rr=π2Dd=39.478Rr在环中心上球带体R-球半径r1,r2-底面半径h-腰高h1-球心O至带底圆心O1的距离V=(3R12+3r22+h2)S1=2πRhS=2πRh+π(r12+r22)Go=h1+h/2桶形D-中间断面直径d-底直径l-桶高对于抛物线形桶体V=(2D2+Dd+d2)对于圆形桶体V=(2D2+d2)在轴交点上椭球体a,b,c-半轴V=abcπS=2*b*在轴交点上多面体的体积和表面积公式形状图形尺寸符号体积V、底面积F、表面积S、侧表面积S1重心G 备注交叉圆柱体r-圆柱半径l1,l-圆柱长V=πr2(l+l1-)在二轴交点上梯形体a,b-下底边长a1,b1-上底边长h-上、下底边距离（高）V=[(2a+a1)b+(2a1+a)b1]=[ab+(a+a1)(b+b1)+a1b1]。

多面体的表面积与体积计算多面体是指由若干个平面多边形组成的立体图形，其中多边形的边之间都相交或者相接。

多面体有很多种类，包括三棱锥、四棱锥、五棱锥、六棱锥、正方体、正八面体等等。

计算多面体的表面积和体积是数学中的一个重要问题，它不仅在几何学中有着广泛的应用，也在工程、建筑等领域中起到重要的作用。

一、多面体的表面积计算表面积是指多面体的所有面的面积之和。

不同种类的多面体的表面积计算方法略有不同。

1. 三棱锥的表面积计算三棱锥的表面积计算公式为：S = 底面积 + 三个侧面积其中，底面积可以用三角形面积计算公式求得，而三个侧面积可以通过底面上的顶点到底面三边的距离和底面三边的长度计算得出。

2. 四棱锥的表面积计算四棱锥的表面积计算公式为：S = 底面积 + 四个侧面积其中，底面积可以用四边形面积计算公式求得，而四个侧面积可以通过底面上的顶点到底面四边的距离和底面四边的长度计算得出。

3. 六棱锥的表面积计算六棱锥的表面积计算公式为：S = 底面积 + 六个侧面积其中，底面积可以用六边形面积计算公式求得，而六个侧面积可以通过底面上的顶点到底面六边的距离和底面六边的长度计算得出。

4. 正方体的表面积计算正方体的表面积计算公式为：S = 6 * 边长的平方其中，正方体的每个面都是一个正方形，所以可以直接将一个正方形的面积乘以6得到整个正方体的表面积。

5. 正八面体的表面积计算正八面体的表面积计算公式比较复杂，可以通过将正八面体划分为不同的三角形、正方形等来计算各个面的面积，然后将各个面积相加得到整个正八面体的表面积。

二、多面体的体积计算体积是指多面体所占的空间大小，可以理解为多面体内部的容积。

不同种类的多面体的体积计算方法也有所不同。

1. 三棱锥的体积计算三棱锥的体积计算公式为：V = 底面积 * 高 / 3其中，底面积可以用三角形面积计算公式求得，高是三棱锥的高度。

2. 四棱锥的体积计算四棱锥的体积计算公式为：V = 底面积 * 高 / 3其中，底面积可以用四边形面积计算公式求得，高是四棱锥的高度。

多面体的体积和表面积计算公式大
全(共6页)
--本页仅作为文档封面，使用时请直接删除即可--
--内页可以根据需求调整合适字体及大小--
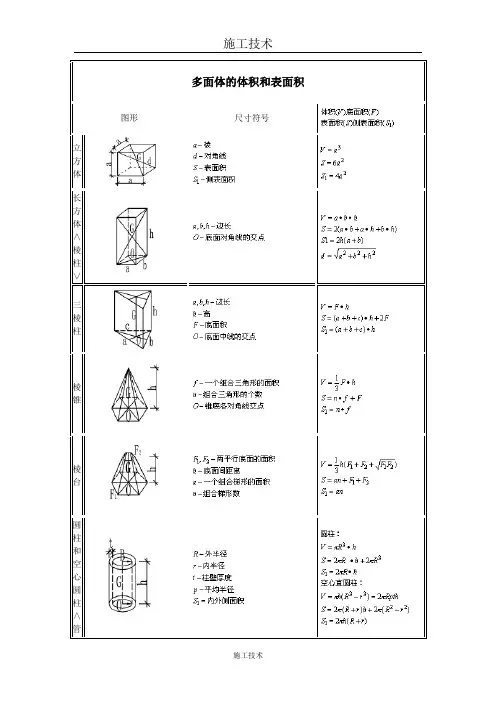
多面体的体积和表面积图形尺寸符号
立
方
体
长
方
体
∧
棱
柱
∨
三
棱
柱
棱
锥
棱
台
圆
柱
和
空
心
圆
柱
∧
管
∨
斜线直圆柱
直圆锥
圆台
球
球扇形∧球楔∨球缺
圆环体∧胎∨
球
带
体
桶
形
椭
球
体
a,b,c-半轴
交
叉
圆
柱
体
梯
形
体
常用图形求面积公式
图形尺寸符号面积（F）表面积
（S）
正方形
长方形
三角形
平行四边形
任意四边形
正多边形
菱形梯形圆形
椭圆
a·b-主轴F= (π/4) a·b
形
扇形
弓形
圆环
部分
圆环
新月
形
L d/102d/10 3d/10 4d/105d/10 6d/10 7d/10 P
抛物线形
等多边形。