六年级分数简便运算分类讲义

六年级数学上册分数简便计算Prepared on 22 November 2020分数简便运算常见题型第一种：连乘——乘法交换律的应用例题：1）1474135⨯⨯ 2）56153⨯⨯ 3）266831413⨯⨯ 涉及定律：乘法交换律 b c a c b a ⋅⋅=⋅⋅基本方法：将分数相乘的因数互相交换，先行运算。

第二种：乘法分配律的应用例题：1）27)27498(⨯+ 2）4)41101(⨯+ 3）16)2143(⨯+ 涉及定律：乘法分配律 bc ac c b a ±=⨯±)(基本方法：将括号中相加减的两项分别与括号外的分数相乘，符号保持不变。

第三种：乘法分配律的逆运算例题：1）213115121⨯+⨯ 2）61959565⨯+⨯ 3）751754⨯+⨯ 涉及定律：乘法分配律逆向定律 )(c b a c a b a ±=⨯±⨯基本方法：提取两个乘式中共有的因数，将剩余的因数用加减相连，同时添加括号，先行运算。

第四种：添加因数“1”例题：1）759575⨯- 2）9216792⨯- 3）23233117233114+⨯+⨯ 涉及定律：乘法分配律逆向运算基本方法：添加因数“1”，将其中一个数n 转化为1×n 的形式，将原式转化为两两之积相加减的形式，再提取公有因数，按乘法分配律逆向定律运算。

第五种：数字化加式或减式例题：1）16317⨯ 2）19718⨯ 3）316967⨯ 涉及定律：乘法分配律逆向运算基本方法：将一个大数转化为两个小数相加或相减的形式，或将一个普通的数字转化为整式整百或1等与另一个较小的数相加减的形式，再按照乘法分配律逆向运算解题。

注意：将一个数转化成两数相加减的形式要求转化后的式子在运算完成后依然等于原数，其值不发生变化。

例如：999可化为1000-1。

其结果与原数字保持一致。

第六种：带分数化加式例题：1）4161725⨯ 2）351213⨯ 3）135127⨯ 涉及定律：乘法分配律基本方法：将带分数转化为整数部分和分数部分相加的形式，再按照乘法分配律计算。

六年级上册第一讲 分数乘法简便运算专题简析：计算过程中，我们先整体地分析算式的特点，然后进行一定的转化，创造条件运用乘法分配律来简算，这种思考方法在四则运算中用处很大。

第一种：乘法分配律的应用 例题：1）27)27498(⨯+ 2）4)41101(⨯+练习：（ 34 ＋58 ）×32 42×（65－74）(32＋43－21)×12 16)2143(⨯+第二种：乘法分配律的逆运算 例题：1）213115121⨯+⨯ 2）61959565⨯+⨯ 3）23233117233114+⨯+⨯练习：59 × 34 ＋59 × 14 53×914－94×53 910 ×1317 ＋910 × 417751754⨯+⨯ 759575⨯- 9216792⨯-第三种：数字化加式或减式 例题：1）16317⨯2）316967⨯练习：36×937 2008×20062007 46×454417× 916第四种：带分数化加式 计算：73115 ×18练习：计算下面各题：64117 ×19 22120 ×121 17 ×5716 4113 ×34 +5114 ×45第五种：乘法交换律与乘法分配律的综合运用计算：15 ×27+35 ×41练习：计算下面各题：14 ×39+34 ×27 16 ×35+56 ×17 18 ×5+58 ×5+18 ×10117 ×49 +517 ×19 17 ×34 +37 ×16 +67 ×112家庭作业3536 ×29 73×2372 49111 ×16 23 ×46+13 ×2819 ×311 +49 ×211 17 ×20+47 ×16 433 ×133 ******** ×20001315 ×56 +2827 ×79 413 ×2+113 ×6+213 ×6 111 ×6+311 ×7+2×311511 ×120 +311 ×12 +511 ×15 43×52+43×0.4 257×101-2571113 －1113 ×1333 19718⨯ 59 ×791617 +50×19 +19 ×517517 ×38 +115 ×716 +115 ×312 1981361961311⨯+⨯ 1381137138137137⨯+⨯资料赠送以下资料考试知识点技巧大全一、考试中途应饮葡萄糖水大脑是记忆的场所，脑中有数亿个神经细胞在不停地进行着繁重的活动,大脑细胞活动需要大量能量。

人教版数学五升六暑期精编专项讲义—新课衔接站第一单元《分数乘法》第4课《分数的混合运算和简便运算》学习目标：1.掌握分数乘加.乘减混合运算的运算顺序。

2.会用整数乘法的运算定律推广运用到分数乘法.并使一些计算简便。

新知讲解：【典例引入】（2018秋•黄山区校级月考）20减少它的是多少？正确列式是（）A．20﹣B．20×C．20﹣20×【分析】求一个数的几分之几用乘法.一个数减少多少用减法．【解答】解：20减少它的列式为：20﹣20×.故选：C．【变式训练】（2014秋•瑞安市校级期中）×+×简算可以运用运算定律是乘法分配律．【分析】依据乘法分配律的意义：求一个数同两个数分别相乘.再把求得的积相加.可以先求这两个数的和.再用这个数与求得的和相乘.结果不变即可解答．【解答】解：×+×＝（+）×＝3×＝1．故答案为：乘法分配律．【知识点总结】（一）分数乘法混合运算1.分数乘法混合运算顺序与整数相同.先乘.除后加.减.有括号的先算括号里面的.再算括号外面的。

2.整数乘法运算定律对分数乘法同样适用.运算定律可以使一些计算简便。

乘法交换律：a×b=b×a乘法结合律：(a×b)×c=a×(b×c)乘法分配律：a×(b±c)=a×b±a×c（二）倒数的意义：乘积为1的两个数互为倒数。

1.倒数是两个数的关系.它们互相依存.不能单独存在。

单独一个数不能称为倒数。

（必须说清谁是谁的倒数）2.判断两个数是否互为倒数的唯一标准是：两数相乘的积是否为“1”。

例如：a×b=1则a.b互为倒数。

3.求倒数的方法：①求分数的倒数：交换分子.分母的位置。

②求整数的倒数：整数分之1。

③求带分数的倒数：先化成假分数.再求倒数。

④求小数的倒数：先化成分数再求倒数。

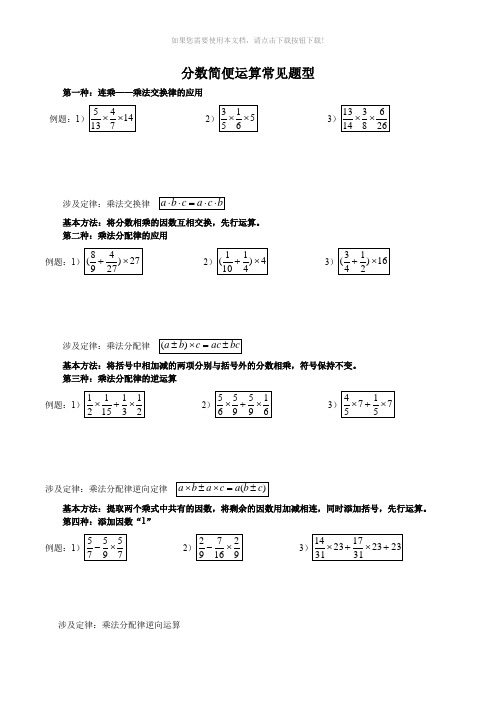
分数简便运算常见题型第一种：连乘——乘法交换律的应用例题：123涉及定律：乘法交换律基本方法：将分数相乘的因数互相交换，先行运算。

第二种：乘法分配律的应用例题：123涉及定律：乘法分配律基本方法：将括号中相加减的两项分别与括号外的分数相乘，符号保持不变。

第三种：乘法分配律的逆运算例题：123涉及定律：乘法分配律逆向定律基本方法：提取两个乘式中共有的因数，将剩余的因数用加减相连，同时添加括号，先行运算。

第四种：添加因数“1”例题：123涉及定律：乘法分配律逆向运算基本方法：添加因数“1”，将其中一个数n转化为1×n的形式，将原式转化为两两之积相加减的形式，再提取公有因数，按乘法分配律逆向定律运算。

第五种：数字化加式或减式例题：123涉及定律：乘法分配律逆向运算基本方法：将一个大数转化为两个小数相加或相减的形式，或将一个普通的数字转化为整式整百或1等与另一个较小的数相加减的形式，再按照乘法分配律逆向运算解题。

注意：将一个数转化成两数相加减的形式要求转化后的式子在运算完成后依然等于原数，其值不发生变化。

例如：999可化为1000-1。

其结果与原数字保持一致。

第六种：带分数化加式例题：123涉及定律：乘法分配律基本方法：将带分数转化为整数部分和分数部分相加的形式，再按照乘法分配律计算。

第七种：乘法交换律与乘法分配律相结合例题：123涉及定律：乘法交换律、乘法分配律逆向运算基本方法：将各项的分子与分子（或分母与分母）互换，通过变换得出公有因数，按照乘法分配律逆向运算进行计算。

注意：只有相乘的两组分数才能分子和分子互换，分母和分母互换。

不能分子和分母互换，也不能出现一组中的其中一个分子（或分母）和另一组乘式中的分子（或分母）进行互换。

第八种：分数乘法和分数除法的简便计算例题：1）基本方法：将分数除法转化成分数乘法再进行计算，乘法分配律。

分数简便运算（能简算的简算）59 × 34 ＋59 × 14 （ 34 ＋58 ）×32 15 ＋ 29 × 310 44－72×512 23 ＋( 47 ＋ 12 )×7252008×2006200738 +38 ×47 +38 ×372534 ×4= 54×（89 - 56 ) 229 ×(15×2931)1113 －1113 ×1333 （ 38 －0.125）×41318（注：可编辑下载，若有不当之处，请指正，谢谢!）。

人教版数学六年级上册说课稿-第1单元分数乘法-第7课时分数简便运算一. 教材分析分数乘法是小学数学中的重要内容，它不仅涉及到分数的运算规则，还涉及到乘法分配律等数学思想。

在本节课中，我们以分数简便运算为主题，通过分数乘法的学习，让学生掌握分数乘法的运算规则，以及灵活运用乘法分配律进行简便运算。

教材通过丰富的例题和练习题，帮助学生巩固所学知识，提高解决问题的能力。

二. 学情分析六年级的学生已经掌握了分数的基本概念和运算规则，对乘法分配律有一定的了解。

但学生在实际操作中，可能会对分数乘法的运算规则理解不深，对乘法分配律的应用还不够灵活。

因此，在教学过程中，我们需要注重引导学生理解分数乘法的运算规则，培养学生运用乘法分配律进行简便运算的能力。

三. 说教学目标1.知识与技能目标：学生能理解分数乘法的运算规则，掌握分数乘法的运算方法，能灵活运用乘法分配律进行简便运算。

2.过程与方法目标：通过自主学习、合作交流，培养学生解决问题的能力。

3.情感态度与价值观目标：培养学生对数学的兴趣，感受数学的乐趣。

四. 说教学重难点1.教学重点：分数乘法的运算规则，分数乘法的运算方法。

2.教学难点：乘法分配律在分数简便运算中的应用。

五. 说教学方法与手段本节课采用自主学习、合作交流的教学方法，利用多媒体课件、例题、练习题等教学手段，帮助学生理解和掌握分数乘法的运算规则，提高学生的运算能力。

六. 说教学过程1.导入新课：通过复习分数的乘法和乘法分配律，引出本节课的主题——分数简便运算。

2.自主学习：学生自主探究分数乘法的运算规则，尝试解决例题。

3.合作交流：学生之间相互讨论，分享解题心得，教师引导学生运用乘法分配律进行简便运算。

4.巩固练习：学生完成练习题，教师及时给予反馈，巩固所学知识。

5.课堂小结：教师引导学生总结本节课所学内容，加深对分数乘法运算规则的理解。

6.课后作业：布置适量作业，让学生巩固所学知识，提高运算能力。

六年级上册分数乘法简便计算专项讲解、典型题型与练习一、分数乘法的简便计算需要熟记的基本知识。

1、四则运算定律① a＋b＝b＋a（加法交换律）＋② a＋b＋c＝a＋（b＋c）（加法结合律）① a－b－c＝a－c－b（减法性质1）－② a－b－c＝a－（b＋c）（减法性质2）① ab＝ba（乘法交换律）×② abc＝a（bc）（乘法结合律）③ a（b±c）＝ab±ac（乘法分配律）① a÷b÷c＝a÷c÷b（除法性质1）÷② a÷b÷c＝a÷（c×b）（除法性质2）2、符号搬家只有同级运算的算式中，数字可以带着运算符号移动位置，计算结果不变。

a＋b－c＝a－c＋b 或a×b÷c＝a÷c×b3、去括号和添括号的法则：（1）加减运算：在只有加减运算的算式里，如果括号前面是“＋”号，则不论去掉括号或添上括号，括号里面的算式运算符号都不变；如果括号前面是“－”号，则不论去掉括号或添上括号，括号里面的运算符号都要改变，即“＋”变“－”，“－”变“＋”，如：a＋（b＋c＋d）＝a＋b＋c＋da－（b＋c＋d）＝a－b－c－da－（b－c）＝a－b＋c（2）乘除运算：在只有乘除运算的算式里，如果括号前面是“×”号，则不论去掉括号或添上括号，括号里面的算式运算符号都不变；如果括号前面是“÷”号，则不论去掉括号或添上括号，括号里面的运算符号都要改变，即“×”变“÷”，“÷”变“×”，如：a×（b×c×d）＝a×b×c×da÷（b×c×d）＝a÷b÷c÷da÷（b÷c）＝a÷b×c注意：每个数前面的运算符号就是这个数的符号，如算式3.9÷（1.3×5）中，×5，而3.9和1.3前面虽然没有符号，其实是省略了×号。

第六讲 六年级数学简便算法6―1、六年级分数加减运算（一）、分数加减法运算法则分数加法与整数加法意义相同；都是把两个数合并成一个数的运算。

分数减法与整数减法意义相同；都是已知两个加数的和与其中的一个加数；求另一个加数的运算。

①、同分母分数加、减法。

同分母分数相加、减；分母不变；只把分子相加减。

即 521041031103101==+=+ ②、异分母分数加、减法：异分母分数相加、减；先通分；然后按照同分母分数加、减法的法则进行计算。

即402340154088351=+=+ ③、带分数相加、减法：现可先把整数部分与分数部分分别相加、减；再把所得的数合并起来。

即87870)8289()33(823893823814413814=+=-+-=-=-=- ④、分数、小数加减混合运算：一是；能将算式中所有的分数都能化成有限小数的；把分数化成小数计算比较简便；这是因为减少了通分的麻烦。

即32.145.325.551145.3415=+-=+- 另一是；不能将算式中的分数化成有限小数的；可以把小数化成分数计算。

即 20194201232011853355.8=-=- （二）、分数加减法运算例题例6-1-1： 计算： 4.75 - 9.63 +（8.25 - 1.37）［思路分析］：先去掉小括号；使4.75和8.25相加凑整；再运用减法的性质：a – b - c = a -（b + c ）；使运算过程简便。

4.75 - 9.63 +（8.25 - 1.37）= 4.75 + 8.25 - 9.63 - 1.37= 13 -（9.63 + 1.37）= 13–11= 2例6-1-2： 计算： 1234 + 2341 + 3412 + 4123［思路分析］：整体观察全式；可以发现题中的4个四位数均由数1、2、3、4组成；且4个数字在每个数位上各出现一次。

1234 + 2341 + 3412 + 4123= 1×1111 + 2×1111 + 3×1111 + 4×1111=（1 + 2 + 3 + 4）×1111= 10×1111= 11110例6-1-3： 计算： 561542133011209127311-+-+- ［思路分析］：因为4131127+=；5141209+=；61513011+=；……。