蒋中一数理经济学的基本方法第4版课后习题详解

第11章多于一个选择变量的情况练习11.2运用教材表11.1分别求下列四个函数的极值，并确定其为极大值还是极小值。

1．z＝x2＋xy＋2y2＋3。

解：首先求出所有一阶、二阶导数，f x＝2x＋y，f y＝x＋4y，f xx＝2，f xy＝1，f yy＝4。

由最大化一阶条件：2x＋y＝0以及x＋4y＝0，解得x*＝0，y*＝0，则z*＝3。

又f xx＞0，f yy＞0，f xx f yy＞f xy2，故函数存在极小值3。

2．z＝－x2－y2＋6x＋2y。

解：首先求出所有一阶、二阶导数，f x＝－2x＋6，f y＝－2y＋2，f xx＝－2，f yy＝－2，f xy ＝0。

由最大化一阶条件：－2x＋6＝0及－2y＋2＝0，解得x*＝3，y*＝1，z*＝10。

又f xx ＜0，f yy＜0，f xx f yy＞f xy2。

故函数存在极大值10。

3．z＝ax2＋by2＋c，考察下面三种情况：（a）a＞0，b＞0；（b）a＜0，b＜0；（c）a与b符号相反。

解：首先求出所有一阶、二阶导数，f x＝2ax，f y＝2by，f xx＝2a，f yy＝2b，f xy＝0，由最大化一阶条件：2ax＝0，以及2by＝0，解得x*＝0，y*＝0，则z*＝c。

（a）当a＞0，b＞0，有f xx＞0，f yy＞0，f xx f yy＞f xy2，故函数有极小值c。

（b）当a＜0，b＜0，有f xx＜0，f yy＜0，f xx f yy＞f xy2，故函数有极大值c。

（c）当a与b符号相反，有f xx f yy＜f xy2，故z*为鞍点。

4．z＝e2x－2x＋2y2＋3。

解：首先求出所有一阶、二阶导数，f x＝2e2x－2，f y＝4y，f xx＝4e2x，f yy＝4，f xy＝0，由最大化一阶条件：2e2x－2＝0及4y＝0，解得x*＝0，y*＝0，则z*＝4。

又因为f xx＞0，f yy ＞0，f xx f yy＞f xy2，故函数有极小值4。

计量经济学（第四版）习题参考答案潘省初第一章 绪论1.1 试列出计量经济分析的主要步骤。

一般说来，计量经济分析按照以下步骤进行：（1）陈述理论（或假说） （2）建立计量经济模型 （3）收集数据 （4）估计参数 （5）假设检验 （6）预测和政策分析 1.2 计量经济模型中为何要包括扰动项?为了使模型更现实，我们有必要在模型中引进扰动项u 来代表所有影响因变量的其它因素，这些因素包括相对而言不重要因而未被引入模型的变量，以及纯粹的随机因素。

1.3什么是时间序列和横截面数据? 试举例说明二者的区别。

时间序列数据是按时间周期（即按固定的时间间隔）收集的数据，如年度或季度的国民生产总值、就业、货币供给、财政赤字或某人一生中每年的收入都是时间序列的例子。

横截面数据是在同一时点收集的不同个体（如个人、公司、国家等）的数据。

如人口普查数据、世界各国2000年国民生产总值、全班学生计量经济学成绩等都是横截面数据的例子。

1.4估计量和估计值有何区别？估计量是指一个公式或方法，它告诉人们怎样用手中样本所提供的信息去估计总体参数。

在一项应用中，依据估计量算出的一个具体的数值，称为估计值。

如Y就是一个估计量，1nii YY n==∑。

现有一样本，共4个数，100，104，96，130，则根据这个样本的数据运用均值估计量得出的均值估计值为5.107413096104100=+++。

第二章 计量经济分析的统计学基础2.1 略，参考教材。

2.2请用例2.2中的数据求北京男生平均身高的99％置信区间NSS x ==45=1.25 用α=0.05，N-1=15个自由度查表得005.0t =2.947，故99%置信限为 x S t X 005.0± =174±2.947×1.25=174±3.684也就是说，根据样本，我们有99%的把握说，北京男高中生的平均身高在170.316至177.684厘米之间。

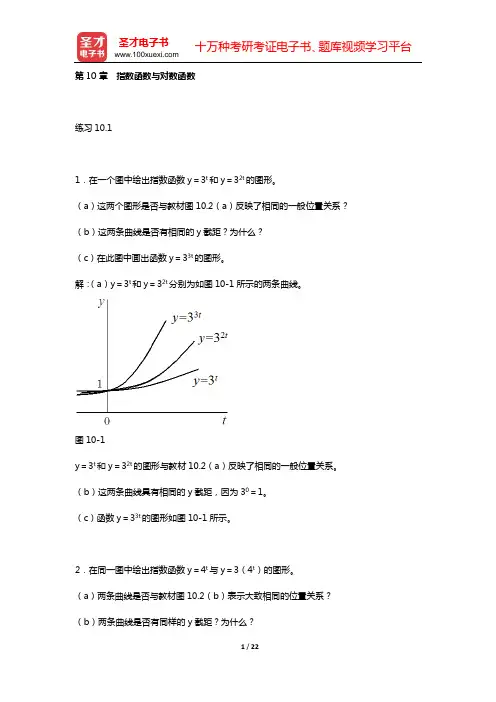
第10章指数函数与对数函数练习10.11．在一个图中绘出指数函数y＝3t和y＝32t的图形。

（a）这两个图形是否与教材图10.2（a）反映了相同的一般位置关系？（b）这两条曲线是否有相同的y截距？为什么？（c）在此图中画出函数y＝33t的图形。

解：（a）y＝3t和y＝32t分别为如图10-1所示的两条曲线。

图10-1y＝3t和y＝32t的图形与教材10.2（a）反映了相同的一般位置关系。

（b）这两条曲线具有相同的y截距，因为30＝1。

（c）函数y＝33t的图形如图10-1所示。

2．在同一图中绘出指数函数y＝4t与y＝3（4t）的图形。

（a）两条曲线是否与教材图10.2（b）表示大致相同的位置关系？（b）两条曲线是否有同样的y截距？为什么？（c）在同一图中绘出函数y＝3（4t）/2的图形。

解：（a）y＝4t和y＝3（4t）曲线为如图10-2所示的两条曲线。

y＝4t和y＝3（4t）的曲线与教材10.2（b）中的曲线有大致相同的位置关系。

图10-2（b）两条曲线不具有同样的y截距，因为40＝1，3×40＝3。

（c）函数y＝3（4t）/2的图形如图10-2所示。

3．认可e t的导数为其自身，运用链式法则求下列函数的dy/dt：（a）y＝e5t；（b）y＝4e3t；（c）y＝6e－2t。

解：（a）dy/dt＝[dy/d（5t）][d（5t）/dt]＝5e5t。

（b）dy/dt＝[dy/d（3t）][d（3t）/dt]＝12e3t。

（c）dy/dt＝[dy/d（－2t）][d（－2t）/dt]＝－12e－2t。

4．根据我们对（10.1）的讨论，你能预期函数y＝e t是以递增速率单调地递增吗？通过确定此函数的一阶和二阶导数的符号验证你的答案。

在验证答案时，记住此函数的定义域为全体实数的集合，即区间（－∞，＋∞）。

解：y′＝e t＞0，y″＝e t＞0。

所以，函数是以递增速率单调地递增。

5．在（10.2）中，若a与c被赋予负值，则教材图10.2中的曲线图形便不再适用。

第20章 最优控制理论练习20.2找出下面问题的控制变量、状态变量和协状态变量的最优路径：1．，且y （0）＝2，y （1）自由。

解：这个问题的哈密尔顿函数为H ＝y －u 2＋λu，对于u 是凹的，并且u 没有任何限制，所以应用一阶条件使H 最大化：∂H/∂u ＝－2u ＋λ＝0，从而u （t ）＝λ/2或y ′＝λ/2①λ的运动方程是λ′＝－∂H/∂y ＝－1，对其积分可解出λ＝c 1－t 。

又横截性条件为λ（1）＝0，从而c 1＝0，最优协状态变量的路径是λ*（t ）＝1－t 。

由①式，得到y′＝（1/2）（1－t ），通过积分得到y （t ）＝（1/2）t －（1/4）t 2＋c 2，通过初始条件y （0）＝2可确定c 2＝2。

这样状态变量的最优路径为y *（t ）＝（1/2）t －（1/4）t 2＋2。

对应的最优控制路径是u *（t ）＝（1/2）（1－t ）。

2．，且y （0）＝10，y （8）自由，u （t ）∈[0，2]。

解：哈密尔顿函数为H ＝6y ＋λ（y ＋u ）＝（6＋λ）y ＋λu ，是关于u 的线性函数，斜率为λ。

为使H 最大化，当λ＞0时，取u ＝2；当λ＜0时，取u ＝0。

λ的运动方程是λ′＝－∂H/∂y ＝－6－λ，该方程的通解是λ（t ）＝Ae －t －6。

通过横截性条()120Max d ..y u t s t y u -' =⎰80Max 6d ..y t s t y y u ' =+⎰件λ（T ）＝λ（8）＝0可以确定A ＝6e 8，从而协状态变量的最优路径是λ*（t ）＝6e 8－t －6。

这是一个关于t 的单减函数，且λ*（8）＝0，从而对于t ∈[0，8]，λ*（t ）≥0。

所以取控制变量u 的最优路径为u *＝2。

由运动方程有y ′＝y ＋u ＝y ＋2，该方程的通解为y （t ）＝ce t －2。

由初始条件y （0）＝10可确定出c ＝12，从而状态变量的最优路径为y *（t ）＝12e t －2。

蒋中一《数理经济学的基本方法》（第4版）课后习题详细分析和解答第17章离散时间：一阶差分方程练习17.21．将下列差分方程变换为（17.2″）的形式。

（a）Δy t＝7（b）Δy t＝0.3y t（c）Δy t＝2y t－9解：（a）y t＋1＝y t＋7。

（b）y t＋1＝1.3y t。

（c）y t＋1＝3y t－9。

2．用迭代法解下列差分方程：（a）y t＋1＝y t＋1（y0＝10）；（b）y t＋1＝αy t（y0＝β）；（c）y t＋1＝αy t－β（当t＝0时，y t＝y0）。

解：（a）y1＝y0＋1，y2＝y1＋1＝y0＋2，y3＝y2＋1＝y0＋3。

不难看出，一般而言，对任意时期t，y t＝y0＋t＝10＋t。

（b）y1＝αy0，y2＝αy1＝α2y0，y3＝αy2＝α3y0。

不难看出，一般而言，对任意时期t，y t＝αt y0＝βαt。

（c）y 1＝αy 0－β，y 2＝αy 1－β＝α2y 0－αβ－β，y 3＝αy 2－β＝α3y 0－α2β－αβ－β。

不难看出，一般而言，对任意时期t，()120=1t t t t y y αβααα---++++ 3．按（17.6）式改写上题中的差分方程，并用公式（17.8′）或（17.9′）解之（哪个方便用哪个）。

答案与用迭代法求得的答案一致吗？解：（a）改写：y t＋1－y t ＝1（y 0＝10）。

a＝－1，c＝1，由（17.9′），定解为y t ＝y 0＋ct＝10＋t。

答案与用迭代法求得的答案一致。

（b）改写：y t＋1－αy t ＝0（y 0＝β）。

a＝－α，c＝0。

若α≠1，由（17.8′），定解为y t ＝y 0αt ＝βαt 。

若α＝1，则a＝－1，由（17.9′），定解为y t ＝y 0＋ct＝β。

不难发现，定解的形式可以统一为y t ＝βαt 。

答案与用迭代法求得的答案一致。

（c）改写：y t＋1－αy t ＝－β（当t＝0时，y t ＝y 0）。

第9章最优化：一类特殊的均衡分析练习9.21．假设定义域为全部实数的集合，求下列函数的稳定值，并检验其为相对极大值、极小值还是拐点：（a）y＝－2x2＋8x＋7；（b）y＝5x2＋x；（c）y＝3x2＋3；（d）y＝3x2－6x＋2。

解：（a）令y′＝－4x＋8＝0，解得x＝2。

当x＜2时，y′＞0；当x＞2时，y′＜0。

所以，稳定值y＝－2×22＋8×2＋7＝15是函数的极大值。

（b）令y′＝10x＋1＝0，解得x＝－1/10。

当x＜－1/10时，y′＜0；当x＞－1/10时，y′＞0。

所以，稳定值y＝5×（－1/10）2－1/10＝－1/20是函数的极小值。

（c）令y′＝6x＝0，解得x＝0。

当x＜0时，y′＜0；当x＞0时，y′＞0。

所以，稳定值y ＝3是函数的极小值。

（d）令y′＝6x－6＝0，解得x＝1。

当x＜1时，y′＜0；当x＞1时，y′＞0。

所以，稳定值y＝3×1－6×1＋2＝－1是函数的极小值。

2．假设定义域为区间[0，∞），求下列函数的稳定值，并检验其为相对极小值、极大值，还是拐点：（a）y＝x3－3x＋5；（b）y＝x3/3－x2＋x＋10；（c）y＝－x3＋4.5x2－6x＋6。

解：（a）令y′＝3x2－3＝0，解得x＝1。

当0≤x＜1时，y′＜0；当x＞1时，y′＞0。

所以，稳定值y＝1－3＋5＝3是函数的极小值。

（b）令y′＝x2－2x＋1＝0，解得x＝1。

当0≤x＜1时，y′＞0；当x＞1时，y′＞0。

所以，稳定值y＝1/3－1＋1＋10＝31/3是函数的拐点。

（c）令y′＝－3x2＋9x－6＝0，解得x1＝1，x2＝2。

当0≤x＜1时，y′＜0；当1＜x＜2时，y′＞0；当x＞2时，y′＜0。

所以，稳定值y＝－1＋4.5－6＋6＝3.5是函数的极小值，稳定值y＝－23＋4.5×22－6×2＋6＝4是函数的极大值。