平行线及其判定(证明应用题)

平行线的判定练习题一、选择题1. 以下哪项不是平行线的基本判定条件？A. 同位角相等B. 内错角相等C. 同旁内角互补D. 两直线相交2. 如果两条直线相交，它们的角度关系是：A. 同位角相等B. 内错角相等C. 同旁内角互补D. 两直线不平行3. 根据平行线判定定理，以下哪项说法是错误的？A. 同位角相等，两直线平行B. 内错角相等，两直线平行C. 同旁内角互补，两直线平行D. 两直线不相交，则它们平行4. 已知直线AB与CD平行，若直线EF与AB相交，则EF与CD的关系是：A. 一定相交B. 可能相交C. 可能平行D. 一定平行5. 如果两条直线的斜率相等，那么它们：A. 一定相交B. 一定平行C. 可能相交D. 可能平行二、填空题1. 根据平行线判定定理，如果两条直线的______相等，则它们平行。

2. 两条平行线之间的距离处处______。

3. 在同一平面内，如果两条直线不相交，则它们______。

4. 如果两条直线的同旁内角不互补，则它们______。

5. 两条直线的斜率不相等，则它们______。

三、判断题1. 如果两条直线的同位角不相等，则它们一定相交。

（对/错）2. 两条平行线与第三条直线相交，同位角一定相等。

（对/错）3. 两条直线的内错角不相等，它们一定不平行。

（对/错）4. 两条直线的同旁内角相等，它们一定相交。

（对/错）5. 如果两条直线的斜率相等，它们可能平行。

（对/错）四、解答题1. 已知直线l1: y = 2x + 3与直线l2: y = 2x + b平行，请求解b 的值。

2. 如果直线AB与CD平行，且AB与EF相交，求证EF与CD也平行。

3. 已知直线m: y = -3x + 5与n: y = -3x + c，判断m与n是否平行，并说明理由。

4. 证明：如果两条直线的斜率相等，则它们一定平行。

5. 已知两条平行线AB与CD，若直线EF与AB相交，求证EF与CD的交点与AB与CD的交点在一条直线上。

平行线的判定练习题(有答案)平行线的判定专项练习60题（有答案)1．已知：如图，BE平分∠ABC，∠1=∠2．求证：BC∥DE．2．如图，已知∠A=∠F，∠C=∠D，试说明BD∥CE．3．如图所示，AB⊥BC，BC⊥CD，BF和CE是射线，并且∠1=∠2，试说明BF∥CE．4．如图，AB⊥BC，∠1+∠2=90°，∠2=∠3，求证：BE∥DF．5．如图，OP平分∠MON，A、B分别在OP、OM上，∠BOA=∠BAO，那么AB平行于ON吗？若平行，请写出证明过程；若不平行，请说明理由．6．已知：如图，∠1=∠2，∠A=∠C．求证：AE∥BC．平行线的判定--- 第 1 页共 1 页7．已知，如图B、D、A在一直线上，且∠D=∠E，∠ABE=∠D+∠E，BC是∠ABE的平分线，求证：DE∥BC．8．如图，已知∠AEC=∠A+∠C，试说明：AB∥CD．9．如图，已知AC∥ED，EB平分∠AED，∠1=∠2，求证：AE∥BD．10．如图，直线AB、CD与直线EF相交于E、F，已知：∠1=105°，∠2=75°，求证：AB∥CD．11．如图，∠D=∠A，∠B=∠FCB，求证：ED∥CF．12．如图，已知AB⊥BC，CD⊥BC，∠1=∠2，求证：EB∥FC．平行线的判定---第 2 页共 2 页13．如图所示所示，已知BE是∠B的平分线，交AC于E，其中∠1=∠2，那么DE∥BC吗？为什么？14．如图，已知∠C=∠D，DB∥EC．AC与DF平行吗？试说明你的理由．15．如图，AC⊥AE，BD⊥BF，∠1=35°，∠2=35°，求证：AE∥BF．16．如图，已知AB∥CD，∠1=∠2，求证：BE∥CF．17．已知∠BAD=∠DCB，∠1=∠3，求证：AD∥BC．18．如图，AD是三角形ABC的角平分线，DE∥CA，并且交AB与点E，∠1=∠2，DF与AB是否平行？为什么？平行线的判定---第 3 页共 3 页19．如图，已知：∠C=∠DAE，∠B=∠D，那么AB平行于DF吗？请说明理由．20．如图，已知点B在AC上，BD⊥BE，∠1+∠C=90°，问射线CF与BD平行吗？说明理由．21．已知∠1的度数是它补角的3倍，∠2等于45°，那么AB∥CD吗？为什么？22．已知：如图，BDE是一条直线，∠ABD=∠CDE，BF平分∠ABD，DG平分∠CDE，求证：BF∥DG．23．如图，四边形ABCD中，∠A=∠C=90°，BF、DE分别平分∠ABC、∠ADC．判断DE、BF是否平行，并说明理由．24．如图，若∠CAB=∠CED+∠CDE，求证：AB∥CD．25．如图，CD⊥AB，GF⊥AB，∠1=∠2．试说明DE∥BC．平行线的判定---第 4 页共 4 页26．如图所示，∠CAD=∠ACB，∠D=90°，EF⊥CD．试说明：∠AEF=∠B．27．已知：如图所示，C，P，D三点在同一条直线上，∠BAP+∠APD=180°，∠E=∠F，求证：∠1=∠2．28．如图，∠D=∠1，∠E=∠2，DC⊥EC．求证：AD∥BE．29．如图，在四边形ABCD中，∠A=∠C，BE平分∠ABC，DF平分∠ADC，试说明BE∥DF．30．已知：如图，∠1=∠2，∠A=∠F，则∠C与∠D相等吗？试说明理由．31．如图，在四边形ABCD中，∠A=∠C=90°，∠1=∠2，∠3=∠4，求证：BE∥DF．平行线的判定---第 5 页共 5 页平行线测姓名：一、选择题1．下列命题中，不正确的是____ [ ]A．两条直线被第三条直线所截，如果同位角相等，那么这两条直线平行B．两条直线被第三条直线所截，如果同旁内角互补，那么这两条直线平行C．两条直线被第三条直线所截，那么这两条直线平行D．如果两条直线都和第三条直线平行，那么这两条直线也互相平行2．如图，可以得到DE∥BC的条件是______ [ ]（2题）（5题）（3题）(7题) （8题）A．∠ACB=∠BAC B．∠ABC+∠BAE=180° C．∠ACB+∠BAD=180°D．∠ACB=∠BAD3．如图，直线a、b被直线c所截，现给出下列四个条件: (1)∠1=∠2(2)∠3=∠6(3)∠4+∠7=180° (4)∠5+∠8=180°，其中能判定a∥b的条件是_________[ ]A．(1)(3) B．(2)(4)C．(1)(3)(4) D．(1)(2)(3)(4)4．一辆汽车在笔直的公路上行驶，两次拐弯后，行驶的方向与原来的方向相同，这两次拐弯的角度可能是________[ ]A．第一次向右拐40°，第二次向左拐40° B．第一次向右拐50°，第二次向左拐130°C．第一次向右拐50°，第二次向右拐130° D．第一次向左拐50°，第二次向左拐130°5．如图，如果∠1=∠2，那么下面结论正确的是_________．[ ]A．AD∥BC B．AB∥CD C．∠3=∠4 D．∠A=∠C6．同一平面内有四条直线a、b、c、d，若a∥b，a⊥c，b⊥d，则直线c、d的位置关系为（）A．互相垂直 B．互相平行 C．相交 D．无法确定7．如图，在平行四边形ABCD中，下列各式不一定正确的是（）A．∠1+∠2=180° B．∠2+∠3=180° C．∠3+∠4=180° D．∠2+∠4=180°8．如图，AD∥BC，∠B=30°，DB平分∠ADE，则∠DEC的度数为（）A．30° B．60° C．90° D．120°二、填空题 9．如图，由下列条件可判定哪两条直线平行，并说明根据．(1)∠1=∠2，．(2)∠A=∠3，．(3)∠ABC+∠C=180°．10．如果两条直线被第三条直线所截，一组同旁内角的度数之比为3∶2，差为36°，那么这两条直线的位置关系是________．11．同垂直于一条直线的两条直线_______．同一平面内，不重合的两直线的位置关系是。

平行线的证明100道经典习题练习（含答案在卷尾）一、选择题（本大题共64小题，共192.0分）1.一个三角形三个内角的度数之比是1:2:3，则这个三角形一定是()A. 锐角三角形B. 直角三角形C. 钝角三角形D. 等腰直角三角形2.如图，能判断直线AB//CD的条件是()A. ∠1=∠2B. ∠3=∠4C. ∠1+∠3=180∘D. ∠3+∠4=180∘3.如图，点F，E分别在线段AB和CD上，下列条件能判定AB//CD的是()A. ∠1=∠2B. ∠1=∠4C. ∠4=∠2D. ∠3=∠44.如图，直线a//b，直线c与直线a，b分别交于点D，E，射线DF⊥直线c，则图中与∠1互余的角有()A. 4个B. 3个C. 2个D. 1个5.如图，∠BDC=98°，∠C=38°，∠A=37°，∠B的度数是()A. 33°B. 23°C. 27°D. 37°6.命题“垂直于同一条直线的两条直线互相平行”的条件是()．A. 垂直B. 两条直线C. 同一条直线D. 两条直线垂直于同一条直线7.如图，BC//DE，若∠A=35°，∠C=24°，则∠E等于()A. 24°B. 59°C. 60°D. 69°8.在如图所示的四种沿AB进行折叠的方法中，不一定能判断纸带两条边a，b互相平行的是()A. 如图1，展开后测得∠1=∠2B. 如图2，展开后测得∠1=∠2且∠3=∠4C. 如图3，测得∠1=∠2D. 在图④中，展开后测得∠1+∠2=180°9.一次数学活动中，检验两条纸带 ①、 ②的边线是否平行，小明和小丽采用两种不同的方法：如图，小明对纸带 ①沿AB折叠，量得∠1=∠2=50∘;小丽对纸带 ②沿GH折叠，发现GD与GC重合，HF与HE重合.则下列判断正确的是()A. 纸带 ①的边线平行，纸带 ②的边线不平行B. 纸带 ①的边线不平行，纸带 ②的边线平行C. 纸带 ① ②的边线都平行D. 纸带 ① ②的边线都不平行10.对于命题“若a2>b2，则a>b”，下面四组关于a，b的值中，能说明这个命题是假命题的是()A. a=3，b=2B. a=−3，b=2C. a=3，b=−1D. a=−1，b=311.将一个长方形纸片按如图所示折叠，若∠1=40°，则∠2的度数是()A. 40°B. 50°C. 60°D. 70°12.通过观察你能肯定的是()A. 图形中线段是否相等B. 图形中线段是否平行C. 图形中线段是否相交D. 图形中线段是否垂直13.学习了平行线后，小敏想出了过已知直线外一点画这条直线的平行线的新方法，她是通过折一张半透明的纸得到的，如图：从图中可知，小敏画平行线的依据有①两直线平行，同位角相等；②两直线平行，内错角相等；③同位角相等，两直线平行；④内错角相等，两直线平行。

平行线的判定及性质一、【基础知识精讲】1、平行线的判定（1）平行公理：经过直线外一点，有且只有一条直线与已知直线平行. （2）平行公理的推论：平行于同一条直线的两条直线. （3）在同一平面内，垂直于同一条直线的两条直线. （4）同位角相等，两直线平行. （5）内错角相等，两直线平行.（6）同旁内角互补，两直线平行.3、平行线的性质（1）两直线平行，同位角相等. （2）两直线平行，内错角相等.（3）两直线平行，同旁内角互补.二、【例题精讲】专题一：余角、补角、对顶角与三线八角例题1：∠A的余角与∠A的补角互为补角，那么2∠A是（）A．直角 B.锐角 C.钝角 D.以上三种都有可能【活学活用1】如图2-79中，下列判断正确的是（）A.4对同位角，2对内错角，4对同旁内角B.4对同位角，2对内错角，2对同旁内角C.6对同位角，4对内错角，4对同旁内角D.6对同位角，4对内错角，2对同旁内角【活学活用2】如图2-82，下列说法中错误的是( )A.∠3和∠5是同位角B.∠4和∠5是同旁内角C.∠2和∠4是对顶角D.∠1和∠2是同位角【活学活用3】如图,直线AB与CD交于点O,OE⊥AB于O,图中∠1与∠2的关系是（）A.对顶角B.互余C.互补D相等例题2：如果两个角的两边分别平行，而其中一个角比另一个角的4倍少30°，那么这两个角分别是_______.【活学活用4】如图，∠AOC +∠DOE +∠BOF = .专题二：平行线的判定例题3：如图，已知∠EFB+∠ADC=180°，且∠1=∠2，试说明DG ∥AB.1 2A BCDF E G【活学活用】1、长方体的每一对棱相互平行，那么这样的平行棱共有 ( )A ．9对B ．16对 C.18对 D ．以上答案都不对2、已知:如图2-96,DE ⊥AO 于E,BO ⊥AO,FC ⊥AB 于C ，∠1=∠2,求证：DO ⊥AB.3、如图2-97,已知：∠1=∠2=，∠3=∠4，∠5=∠6.求证:AD ∥BC.4、如图2—101，若要能使AB ∥ED ，∠B 、∠C 、∠D 应满足什么条件?ABCDOE F5、同一平面内有四条直线a 、b 、c 、d ，若a ∥b ，a ⊥c ，b ⊥d ，则c 、d 的位置关系为（ ） A.互相垂直 B ．互相平行 C.相交 D ．没有确定关系专题三：平行线的性质1、如图，110,ABC ACB BO ∠+∠=、CO 分别平分ABC ∠和,ACB EF ∠过点O 与BC 平行，则BOC ∠= . 2、如图，AB //CD ，BC //DE ，则∠B+∠D = .3、如图，直线AB 与CD 相交于点O ，OB 平分∠DOE .若60DOE ∠=，则∠AOC 的度数是 .4、 如图，175,2120,375∠=∠=∠=，则4∠= .13 425、如图，//AB CD ，直线EF 分别交AB 、CD 于E 、F ，ED 平分BEF ∠，若172∠=，则2∠= .【例题讲解】例1：如图，已知：AD ∥BC, ∠AEF=∠B,求证：AD ∥EF 。

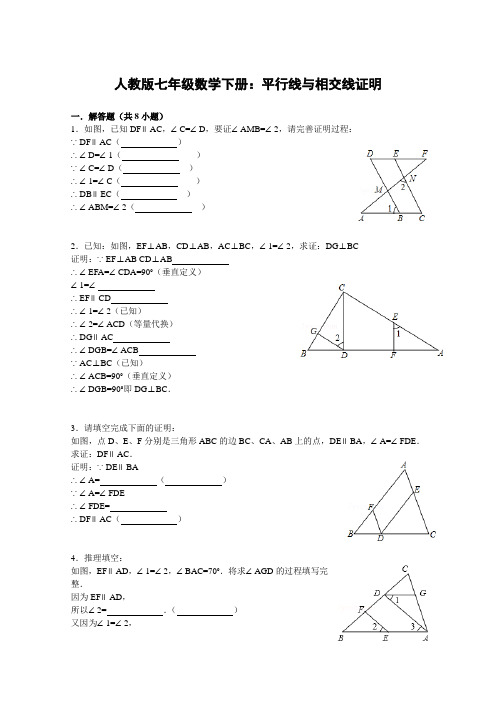
人教版七年级数学下册：平行线与相交线证明一．解答题（共8小题）1．如图，已知DF∥AC，∠C=∠D，要证∠AMB=∠2，请完善证明过程：∵DF∥AC（_________）∴∠D=∠1（_________）∵∠C=∠D（_________）∴∠1=∠C（_________）∴DB∥EC（_________）∴∠ABM=∠2（_________）2．已知：如图，EF⊥AB，CD⊥AB，AC⊥BC，∠1=∠2，求证：DG⊥BC证明：∵EF⊥AB CD⊥AB_________∴∠EFA=∠CDA=90°（垂直定义）∠1=∠_________∴EF∥CD_________∴∠1=∠2（已知）∴∠2=∠ACD（等量代换）∴DG∥AC_________∴∠DGB=∠ACB_________∵AC⊥BC（已知）∴∠ACB=90°（垂直定义）∴∠DGB=90°即DG⊥BC．3．请填空完成下面的证明：如图，点D、E、F分别是三角形ABC的边BC、CA、AB上的点，DE∥BA，∠A=∠FDE．求证：DF∥AC．证明：∵DE∥BA∴∠A=_________（_________）∵∠A=∠FDE∴∠FDE=_________∴DF∥AC（_________）4．推理填空：如图，EF∥AD，∠1=∠2，∠BAC=70°．将求∠AGD的过程填写完整．因为EF∥AD，所以∠2=_________．（_________）又因为∠1=∠2，所以∠1=∠3．（_________）所以AB∥_________．（_________）所以∠BAC+_________=180°（_________）又因为∠BAC=70°，所以∠AGD=_________．5．如图：∠ABC=∠ACB，BD平分∠ABC，CE平分∠ACB，∠DBF=∠F，那么EC与DF平行吗？为什么？请完成下面的解题过程解：∵BD平分∠ABC，CE平分∠ACB （已知）∴∠DBC=∠_________，∠ECB=∠_________∵∠ABC=∠ACB （已知）∴∠_________=∠_________．∠_________=∠_________（已知）∴∠F=∠_________∴EF∥AD_________．6．补全下列推理过程：如图，EF∥AD，∠1=∠2，∠BAC=80°．求∠AGD的度数．因为EF∥AD （已知）所以∠2=_________（_________）又因为∠1=∠2 （已知）所以∠1=∠3（等量代换）所以AB∥_________（_________）所以∠BAC+_________=180°（两直线平行，同旁内角互补）因为∠BAC=80°（已知）所以∠AGD=_________（等量代换）7．完成下面的证明：（1）如图1，点D，E，F分别是三角形ABC的边BC，CA，AB上的点，DE∥BA，DF∥CA．求证：∠FDE=∠A．证明：∵DE∥BA，∴∠FDE=_________（_________），∵DF∥CA，∴∠A=_________（_________），∴∠FDE=∠A；（2）如图2，AB和CD相交于点O，∠C=∠COA，∠D=∠BOD，求证：AC∥BD；证明：∵∠C=∠COA，∠D=∠BOD，∵∠COA=∠BOD（_________），∴∠C=_________，∴AC∥BD（_________）．参考答案与试题解析一．解答题（共8小题）1．如图，已知DF∥AC，∠C=∠D，要证∠AMB=∠2，请完善证明过程：∵DF∥AC（已知）∴∠D=∠1（两直线平行，内错角相等）∵∠C=∠D（已知）∴∠1=∠C（等量代换）∴DB∥EC（同位角相等，两直线平行）∴∠ABM=∠2（两直线平行，同位角相等）考点：平行线的判定与性质．专题：推理填空题．分析：先根据平行线的性质由DF∥AC得到∠D=∠1，再根据等量代换得到∠1=∠C，于是可根据平行线的判定方法得到DB∥EC，然后根据平行线的性质得到∠AMB=∠2．解答：证明：∵DF∥AC（已知），∴∠D=∠1（两直线平行，内错角相等），∵∠C=∠D（已知），∴∠1=∠C（等量代换），∴DB∥EC（同位角相等，两直线平行），∴∠AMB=∠2（两直线平行，同位角相等）．故答案为：已知，两直线平行，内错角相等，已知，等量代换，同位角相等，两直线平行，两直线平行，同位角相等．点评：本题考查了平行线的判定与性质：同位角相等，两直线平行；内错角相等，两直线平行；两直线平行，同位角相等；两直线平行，内错角相等．2．已知：如图，EF⊥AB，CD⊥AB，AC⊥BC，∠1=∠2，求证：DG⊥BC 证明：∵EF⊥AB CD⊥AB已知∴∠EFA=∠CDA=90°（垂直定义）∠1=∠ACD∴EF∥CD（两直线平行，同位角相等）∴∠1=∠2（已知）∴∠2=∠ACD（等量代换）∴DG∥AC（内错角相等，两直线平行）∴∠DGB=∠ACB（两直线平行，同位角相等）∵AC⊥BC（已知）∴∠ACB=90°（垂直定义）∴∠DGB=90°即DG⊥BC．考点：平行线的判定与性质；垂线．专题：推理填空题．分析：根据垂直定义求出∠EFA=∠CDA=90°，求出∠1=∠ACD，推出EF∥CD，根据平行线的性质得出∠2=∠ACD，推出DG∥AC，根据平行线的性质推出∠ACB=∠DGB即可．解答：证明：∵EF⊥AB，CD⊥AB（已知），∴∠EFA=∠CDA=90°（垂直定义），∴EF∥CD（同位角相等，两直线平行），∴∠1=∠ACD（两直线平行，同位角相等），∵∠1=∠2（已知），∴∠2=∠ACD（等量代换），∴DG∥AC（内错角相等，两直线平行），∴∠DGB=∠ACB（两直线平行，同位角相等），∵AC⊥CB，∴∠ACB=90°，∴∠DGB=90°，即DG⊥BC，故答案为：已知，ACD，（两直线平行，同位角相等），（内错角相等，两直线平行），（两直线平行，同位角相等）．点评：本题考查了平行线的判定和性质，三角形内角和定理，垂直定义的应用，主要考查学生的推理能力．3．请填空完成下面的证明：如图，点D、E、F分别是三角形ABC的边BC、CA、AB上的点，DE∥BA，∠A=∠FDE．求证：DF∥AC．证明：∵DE∥BA∴∠A=∠DEC（两直线平行，同位角相等）∵∠A=∠FDE∴∠FDE=∠DEC∴DF∥AC（内错角相等，两直线平行）考点：平行线的判定与性质．专题：推理填空题．分析：根据平行线的性质得出∠A=∠DEC，求出∠FDE=∠DEC，根据平行线的判定推出即可．解答：证明：∵DE∥BA，∴∠A=∠DEC（两直线平行，同位角相等），∵∠A=∠FDE（已知），∴∠FDE=∠DEC（等量代换），∴DF∥AC（内错角相等，两直线平行），故答案为：∠DEC，两直线平行，同位角相等；∠DEC，内错角相等，两直线平行．点评：本题考查了平行线的性质和判定的应用，注意：①两直线平行，同位角相等，②内错角相等，两直线平行．4．推理填空：如图，EF∥AD，∠1=∠2，∠BAC=70°．将求∠AGD的过程填写完整．因为EF∥AD，所以∠2=∠3．（两直线平行，同位角相等）又因为∠1=∠2，所以∠1=∠3．（等量代换）所以AB∥DG．（内错角相等，两直线平行）所以∠BAC+∠AGD=180°（两直线平行，同旁内角互补）又因为∠BAC=70°，所以∠AGD=110°．考点：平行线的判定与性质．专题：推理填空题．分析：根据平行线的性质推出∠1=∠2=∠3，推出AB∥DG，根据平行线的性质得出∠BAC+∠DGA=180°，代入求出即可．解答：解：∵EF∥AD，∴∠2=∠3（两直线平行，同位角相等），∵∠1=∠2，∴∠1=∠3（等量代换），∴AB∥DG（内错角相等，两直线平行），∴∠BAC+∠DGA=180°（两直线平行，同旁内角互补），∵∠BAC=70°，∴∠AGD=110°，故答案为：∠3，两直线平行，同位角相等，等量代换，DG，内错角相等，两直线平行，∠AGD，两直线平行，同旁内角互补，110°．点评：本题考查了平行线的性质和判定的应用，注意：平行线的性质是①两直线平行，同位角相等，②两直线平行，内错角相等，③两直线平行，同旁内角互补，反之亦然．5．如图：∠ABC=∠ACB，BD平分∠ABC，CE平分∠ACB，∠DBF=∠F，那么EC与DF 平行吗？为什么？请完成下面的解题过程解：∵BD平分∠ABC，CE平分∠ACB （已知）∴∠DBC=∠ABC，∠ECB=∠ACB∵∠ABC=∠ACB （已知）∴∠DBC=∠ECB．∠F=∠DBF（已知）∴∠F=∠ECB∴EF∥AD（同位角相等，两直线平行）．考点：平行线的判定．专题：推理填空题．分析：利用角平分线的性质得出∠DBC=∠ABC，∠ECB=∠ACB，进而求出∠F=∠ECB，得出答案即可．解答：解：∵BD平分∠ABC，CE平分∠ACB（已知）∴∠DBC=∠ABC，∠ECB=∠ACB，∵∠ABC=∠ACB （已知）∴∠DBC=∠ECB．∵∠DBF=∠F，（已知）∴∠F=∠ECB，∴EF∥AD（同位角相等，两直线平行）．点评：此题主要考查了平行线的判定以及角平分线的性质，得出∠F=∠ECB是解题关键．6．补全下列推理过程：如图，EF∥AD，∠1=∠2，∠BAC=80°．求∠AGD的度数．因为EF∥AD （已知）所以∠2=∠3（两直线平行，同位角相等）又因为∠1=∠2 （已知）所以∠1=∠3（等量代换）所以AB∥DG（内错角相等，两直线平行）所以∠BAC+∠AGD=180°（两直线平行，同旁内角互补）因为∠BAC=80°（已知）所以∠AGD=100°（等量代换）考点：平行线的判定与性质．专题：推理填空题．分析：根据平行线性质推出∠2=∠3，推出∠1=∠3，根据平行线的判定推出AB∥DG，根据平行线的性质得出∠BAC+∠AGD=180°，代入求出即可．解答：解：∵EF∥AD，∴∠2=∠3（两直线平行，同位角相等），∵∠1=∠2，∴∠1=∠3，∴AB∥DG（内错角相等，两直线平行），∴∠BAC+∠AGD=180°，∵∠BAC=80°，∴∠AGD=100°，故答案为：∠3，两直线平行，同位角相等，DG，内错角相等，两直线平行，∠AGD，100°．点评：本题考查了平行线的性质和判定的应用，注意：平行线的性质是：①两直线平行，同位角相等，②两直线平行，内错角相等，③两直线平行，同旁内角互补，反之亦然．7．完成下面的证明：（1）如图1，点D，E，F分别是三角形ABC的边BC，CA，AB上的点，DE∥BA，DF∥CA．求证：∠FDE=∠A．证明：∵DE∥BA，∴∠FDE=∠BFD（两直线平行，内错角相等），∵DF∥CA，∴∠A=∠BFD（两直线平行，同位角相等），∴∠FDE=∠A；（2）如图2，AB和CD相交于点O，∠C=∠COA，∠D=∠BOD，求证：AC∥BD；证明：∵∠C=∠COA，∠D=∠BOD，∵∠COA=∠BOD（对顶角相等），∴∠C=∠D，∴AC∥BD（内错角相等，两直线平行）．考点：平行线的判定与性质．专题：推理填空题．分析：（1）根据平行线的性质得出∠FDE=∠BFD，∠A=∠BFD，推出即可；（2）根据对顶角相等和已知求出∠C=∠D，根据平行线的判定推出即可．解答：（1）证明：∵DE∥BA，∴∠FDE=∠BFD（两直线平行，内错角相等），∵DF∥CA，∴∠A=∠BFD（两直线平行，同位角相等），∴∠FDE=∠A，故答案为：∠BFD，两直线平行，内错角相等，∠BFD，两直线平行，同位角相等；（2）证明：∵∠C=∠COA，∠D=∠BOD，又∵∠COA=∠BOD（对顶角相等），∴∠C=∠D，∴AC∥BD（内错角相等，两直线平行），故答案为：对顶角相等，∠D，内错角相等，两直线平行．点评：本题考查了平行线的性质和判定的应用，注意：①两直线平行，同位角相等，②两直线平行，内错角相等，③两直线平行，同旁内角互补，反之亦然，题目比较好，难度适中．8．如图，在△ABC中，DE∥BC，连结DC，点F是边BC上一点，GF⊥AB，垂足为G，∠1=∠2，求证：CD⊥AB．考点：平行线的判定与性质；垂线．专题：证明题．分析：求出∠BGF=90°，根据平行线的性质和已知求出∠2=∠BCD，推出FG∥CD，根据平行线的性质得出∠CDB=∠BGF=90°即可．解答：证明：∵FG⊥AB，∴∠BGF=90°，∵DE∥BC，∴∠1=∠BCD，∵∠1=∠2，∴∠2=∠BCD，∴FG∥CD，∴∠CDB=∠BGF=90°，∴CD⊥AB．点评：本题考查了平行线的性质和判定，垂直的定义的应用，主要考查学生的推理能力．。

平行线的性质判定专项练习40题1.已知BE平分∠ABC，且∠1=∠2，要证明BC∥DE。

2.在图中，AB⊥BC，BC⊥CD，BF和CE是两条射线，且∠1=∠2，需要说明XXX。

3.在图中，AB⊥BC，且∠1+∠2=90°，∠2=∠3，要证明BE∥DF。

4.在图中，OP平分∠MON，A、B分别在OP、OM上，且∠BOA=∠BAO，需要判断AB是否平行于ON。

若平行，需要给出证明过程；若不平行，需要说明理由。

5.已知在图中，B、D、A在一直线上，且∠D=∠E，∠XXX∠D+∠E，BC是∠ABE的平分线，要证明DE∥BC。

6.在图中，直线AB、CD与直线EF相交于E、F，已知∠1=105°，∠2=75°，需要证明AB∥CD。

7.已知∠D=∠A，∠B=∠FCB，需要证明ED∥CF。

8.已知∠1的度数是它补角的3倍，∠2等于45°，需要判断AB是否平行于CD。

理由需要说明。

9.在图中，已知AC∥ED，且EB平分∠AED，∠1=∠2，需要证明AE∥BD。

10.在图中，AC⊥AE，BD⊥BF，且∠1=35°，∠2=35°，需要证明AE∥BF。

11.在△ABC中，点D在AB上，且∠XXX∠A，∠BDC的平分线交BC于点E。

需要证明DE∥AC。

12.已知∠XXX∠A+∠C，需要说明AB∥CD。

13.在图中，已知BE是∠B的平分线，交AC于E，且∠1=∠2，需要判断DE是否平行于BC。

理由需要说明。

14.已知∠C=∠D，且DB∥EC。

需要判断AC是否平行于DF。

理由需要说明。

15.直线AB、CD被EF所截，且∠3=∠4，∠1=∠2，XXX。

需要证明AB∥CD。

16.已知AB∥CD，且∠1=∠2，需要证明BE∥CF。

17.已知∠BAD=∠DCB，且∠1=∠3，需要证明AD∥BC。

18.在图中，AD是三角形ABC的角平分线，DE∥CA，并且交AB于点E，且∠1=∠2.需要判断DF是否平行于AB。

精品文档 。 1欢迎下载

平行线的判定与性质综合应用题 1.、已知：BC//EF，∠B=∠E， 求证：AB//DE。

2. 如图，已知MN⊥AB于P，MN⊥CD于Q，∠2=80°，求∠1的度数． 3．已知：如图，∠ADE＝∠B，∠DEC＝115°， 求∠C的度数。

A B E P D C

F

2 1

D C B

A

Q P N M

DE

BC

A精品文档

。 2欢迎下载

4.如图，EB∥DC，∠C=∠E，请你说出∠A=∠ADE的理由。 5、如图：已知： ，求 ∠4的度数 6、如图，AD是∠EAC的平分线，AD∥BC，∠B=30 o， 求∠EAD、∠DAC、∠C的度数。 精品文档

。 3欢迎下载

7．已知：如图⑿，CE平分∠ACD，∠1=∠B， 求证：AB∥CE

8、如图，已知、BE平分∠ABC，∠CBE=25°，∠BED=25°， ∠C=30°，求∠ADE与∠BEC的度数。

9.DE∥BC，CD是∠ACB的平分线，∠B =800，∠ACB=500 ，求∠EDC，∠CDB A

B C D E

E B A D C 精品文档

。 4欢迎下载

10.、如图，AB∥EF，∠B =1350，∠C=670 ，则求∠1的度数． 11．如图，CDAB//，AE平分BAD，CD与AE相交于F,ECFE。 求证：BCAD//。

12．如图，已知CDAB//，40B，CN是BCE的平分线，CNCM，求BCM的度数。

21

F

E

D

CBA

NM

EDC

BA精品文档

。 5欢迎下载

欢迎您的下载， 资料仅供参考！

致力为企业和个人提供合同协议，策划案计划书，学习资料等等 打造全网一站式需求

1．：如图，BE平分∠ABC，∠1=∠2．求证：BC∥DE．4．如图，AB⊥BC，∠1+∠2=90°，∠2=∠3，求证：BE∥DF．2．如图，∠A=∠F，∠C=∠D，试说明BD∥CE．5．如图，OP平分∠MON，A、B分别在OP、OM上，∠BOA=∠BAO，那么AB平行于ON吗？假设平行，请写出证明过程；假设不平行，请说明理由．3．如下图，AB⊥BC，BC⊥CD，BF和CE是射线，6．：如图，∠1=∠2，∠A=∠C．求证：AE∥BC．并且∠1=∠2，试说明BF∥CE．7．，如图B、D、A在一直线上，且∠D=∠E，10．如图，直线AB、CD与直线EF相交于E、F，：∠ABE=∠D+∠E，BC是∠ABE的平分线，∠1=105°，∠2=75°，求证：AB∥CD．求证：DE∥BC．8．如图，∠AEC=∠A+∠C，试说明：AB∥CD．11．如图，∠D=∠A，∠B=∠FCB，求证：ED∥CF．9．如图，AC∥ED，EB平分∠AED，∠1=∠2，12．如图，AB⊥BC，CD⊥BC，∠1=∠2，求证：求证：AE∥BD．EB∥FC．13．如下图所示，BE是∠B的平分线，交AC16．如图，AB∥CD，∠1=∠2，求证：BE∥CF．于E，其中∠1=∠2，那么DE∥BC吗？为什么？14．如图，∠C=∠D，DB∥EC．AC与DF平行吗？17．∠BAD=∠DCB，∠1=∠3，求证：AD∥BC．试说明你的理由．15．如图，AC⊥AE，BD⊥BF，∠1=35°，∠2=35°，求18．如图，AD是三角形ABC的角平分线，DE∥CA，证：AE∥BF．并且交AB与点E，∠1=∠2，DF与AB是否平行？为什么？19．如图，：∠C=∠DAE，∠B=∠D，那么AB平22．：如图，BDE是一条直线，∠ABD=∠CDE，行于DF吗？请说明理由．BF平分∠ABD，DG平分∠CDE，求证：BF∥DG．20．如图，点B在AC上，BD⊥BE，∠1+∠C=90°，23．如图，四边形ABCD中，∠A=∠C=90°，BF、DE问射线CF与BD平行吗？说明理由．分别平分∠ABC、∠ADC．判断DE、BF是否平行，并说明理由．21．∠1的度数是它补角的3倍，∠2等于45°，那么AB∥CD吗？为什么？24．如图，假设∠CAB=∠CED+∠CDE，求证：AB∥CD．25．如图，CD⊥AB，GF⊥AB，∠1=∠2．试说明DE∥BC．28．如图，∠D=∠1，∠E=∠2，DC⊥EC．求证：AD∥BE．26．如下图，∠CAD=∠ACB，∠D=90°，EF⊥CD．试29．如图，在四边形ABCD中，∠A=∠C，BE平分说明：∠AEF=∠B．∠ABC，DF平分∠ADC，试说明BE∥DF．27．：如下图，C，P，D三点在同一条直线上，30．：如图，∠1=∠2，∠A=∠F，那么∠C与∠D相∠BAP+∠APD=180°，∠E=∠F，等吗？试说明理由．求证：∠1=∠2．31．如图，在四边形ABCD中，∠A=∠C=90°，∠1=∠2，34．如图，∠1=∠2，∠C=∠CDO，求证：CD∥OP．∠3=∠4，求证：BE∥DF．32．如图，∠1=∠2求证：a∥b．35．如图，DE平分∠BDF，AF平分∠BAC，且∠1=∠2．求证〔1〕DF∥AC；〔2〕DE∥AF．33．如图，DE⊥AO于E，BO⊥AO于O，FC⊥AB于36．如图，AD平分∠BAC，EF平分∠DEC，且∠1=∠2，试说明DE与AB的位置关系．C，∠1=∠2，找出图中互相平行的线，并加以说明．37．如图，在△ABC中，点D在AB上，∠ACD=∠A，40．如图，直线AB、CD被直线EF所截，∠1+∠4=180°，∠BDC的平分线交BC于点E．求证：AB∥CD．求证：DE∥AC．38．如图，AB与CD相交于点O，并且∠A=∠1，试问41．如下图，：∠1=∠2，∠E=∠F．试说明∠2与∠B满足什么关系时，AC∥BD？说明理由．AB∥CD．39．如图，∠1=∠A，∠2=∠B，那么MN与EF平42．如图，EF⊥CD于F，∠GEF=25°，∠1=65°，行吗？如果平行，请说明理由．那么AB与CD平行吗？请说明理由．43．如图，∠1=∠2=90°，∠3=30°，∠4=60°，图中46．如图，B、C、D三点在同一条直线上，∠B=∠1，有几对平行线？说说你的理由．∠2=∠E，试说明AD∥CE．44．直线AB，CD被直线EF所截，∠1=∠2，直线AB47．直线AB、CD与GH交于E、F，EM平分∠BEF，和CD平行吗？为什么？FN平分∠DFH，∠BEF=∠DFH，求证：EM∥FN．45．：如图，AD⊥BC，EF⊥BC，∠1=∠2．求证：48．如下图，∠ABC=∠BCD，BE、CF分别平分∠ABC和∠BCD，请你说出BE与CF的位置关系，并说出你AB∥GF．的理由．49．如图，假设∠1=∠2，请判断DB与EC的位置关系，52．：如图，∠C=∠1，∠2和∠D互余，BE⊥FD并说明理由．于点G．求证：AB∥CD．50．如图，在△ABC中，CD⊥AB，垂足为D，点E在53．如图，直线AB，CD被EF所截，∠3=∠4，∠1=∠2，BC上，EF⊥AB，垂足为F．EG⊥FG．〔1〕CD与EF平行吗？为什么？求证：AB∥CD．〔2〕如果∠1=∠2，DG∥BC吗？为什么？51．如图，：HG平分∠AHM，MN平分∠DMH，54．：如图，CD是直线，E在直线CD上，∠1=130°，且∠AHM=∠DMH．∠A=50°，求证：AB∥CD．问：GH与MN有怎样的位置关系，请说明理由．〔请注明每一步的理由〕55．如图，∠1=∠2，∠DAB=∠DCA，且DE⊥AC，58．如图，AD⊥BC于点D，∠1=2，∠CDG=∠B，请你判断EF与BC的位置关系，并加以证明，要求写出BF⊥AC，问：〔1〕AD∥BC吗？每步证明的理由．〔2〕AB∥CD吗？为什么？56．如图，四边形ABCD，∠1=30°，∠B=60°，AB⊥AC，59．：如图，CE平分∠ACD，∠1=∠B，求证：那么AD与BC一定平行吗？AB与CD呢？假设平行请说明AB∥CE．理由，反之那么不用说明理由．57．：如图，∠A=∠F，∠C=∠D．60．如图，∠1=∠2，∠3=∠4，可以判定哪两条直求证：BD∥CE．线平行？--------。

初一平行线证明题(精选多篇)第一篇：初一平行线证明题初一平行线证明题用反证法a平面垂直与一条直线，设平面和直线的交点为pb平面垂直与一条直线，设平面和直线的交点为q假设a和b不平行，那么一定有交点。

设有交点r，那么做三角形pqrpr垂直pqqr垂直pq没有这样的三角形。

因为三角形的内角和为180所以a一定平行于b证明：如果a‖b,a‖c,那么b‖c证明:假使b、c不平行则b、c 交于一点o又因为a‖b,a‖c所以过o有b、c两条直线平行于a这就与平行公理矛盾所以假使不成立所以b‖c由同位角相等，两直线平行，可推出：内错角相等，两直线平行。

同旁内角互补，两直线平行。

因为a‖b,a‖c,所以b‖c(平行公理的推论)2“两直线平行，同位角相等.”是公理，是无法证明的，书上给的也只是说明而已，并没有给出严格证明，而“两直线平行，内错角相等“则是由上面的公理推导出来的，利用了对等角相等做了一个替换，上面两位给出的都不是严格的证明。

一、怎样证明两直线平行证明两直线平行的常用定理(性质)有:1.两直线平行的判定定理:①同位角相等,两直线平行;②内错角相等,两直线平行;③同旁内角互补,两直线平行;④平行(或垂直)于同一直线的两直线平行.2、三角形或梯形的中位线定理.3、如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例,那么这条直线平行于三角形的第三边.4、平行四边形的性质定理.5、若一直线上有两点在另一直线的同旁).(a)艺l=匕3(b)/2=艺3(c)匕4二艺5(d)匕2+/4=18)分析:利用平行线判定定理可判断答案选c认六一值!小人﹃夕叱的一试勺洲洲川jlze一b/(一、图月一飞/匕一|求且它们到该直线的距离相等,则两直线平行.例1(2014年南通市)已知:如图l,下列条件中,不能判断直线l,//l:的是(b).例2(2014年泉州市)如图2,△注bc中,匕bac的平分线ad交bc于d,④o过点a,且和bc切于d,和ab、ac分别交b于e、f,设ef交ad于c,连结df.(l)求证:ef//bc(1)根据定义。

1.已知：如图，BE平分/ ABC , /仁/ 2 .求证：BC // DE . 4 .如图，AB 丄BC ,Z 1 + / 2=90 ° / 2= / 3,求证: BE //DF.5 .如图，OP平分/ MON , A、B分别在OP、OM上, /BOA= / BAO，那么AB平行于ON吗？若平行，请写出证明过程；若不平行，请说明理由.3.如图所示，AB丄BC, BC丄CD , BF和CE是射线, 并且/1 = / 2，试说明BF // CE .6.已知：如图，/ 1 = / 2,Z A= / C.求证：AE // BC .7.已知，如图B、D、A在一直线上，且/ D= / E,/ ABE= / D+ / E, BC 是/ ABE 的平分线，10.如图，直线AB、CD与直线EF相交于E、F,已知: / 仁105 ° / 2=75 ° 求证：AB // CD .&如图，已知/ AEC= / A+ / C,试说明：AB // CD . 11.如图，/ D= / A，/ B= / FCB，求证：ED // CF.9.如图，已知AC // ED, EB 平分/ AED，/ 1 = / 2, 求证：AE // BD .12 .如图，已知AB丄BC , CD丄BC ,Z 1= / 2,求证:114.如图，已知/ C=Z D , DB // EC . AC 与DF 平行吗? 试说明你的理由.17 .已知/ BAD= / DCB ，/ 1 = / 3，求证：AD // BC .B C15.如图，AC 丄 AE , BD 丄 BF ，/ 仁35° / 2=35° 求 证：AE // BF .18 .如图，AD 是三角形 ABC 的角平分线，DE // CA , 并且交AB 与点E ,/仁/ 2, DF 与AB 是否平行？为什么？13 •如图所示所示，已知 BE 是/ B 的平分线，交 AC 于E ,其中/ 1 = / 2，那么DE // BC 吗？为什么？16.如图，已知 AB // CD ，/ 1 = / 2，求证: BE // CF.19.如图，已知：/ C= / DAE ，/ B=/ D ，那么 AB 平 行于DF 吗？请说明理由.20 .如图，已知点B 在AC 上，BD 丄BE ，/ 1 + / C=90 ° 问射线CF 与BD 平行吗？说明理由.23.如图，四边形 ABCD 中，/ A= / C=90 ° BF 、DE 分别平分/ ABC 、/ ADC .判断DE 、BF 是否平行，并 说明理由.21.已知/ 1的度数是它补角的 3倍，/ 2等于45°那 么AB // CD吗？为什么？AB // CD .匸BDE 是一条直线，/ ABD= / CDE , DG平分/ CDE ，求证：BF // DG .24.如图，若/ CAB= / CED+ / CDE ，求证:22.已知：如图, BF 平分/ ABD ,25. 如图，CD 丄AB ,GF丄AB，/ 1 = / 2 .试说明DE //BC .28.如图，/ D= / 1, Z E=Z 2, DC丄EC.求证：AD // BE.26. 女口图所示，Z CAD= Z ACB , Z D=90 ° EF± CD .试说明：Z AEF= Z B .29.如图，在四边形ABCD中，Z A= Z C, BE平分Z ABC，DF 平分Z ADC，试说明BE // DF.27. 已知：如图所示，C, P, D三点在同一条直线上,Z BAP+ Z APD=180 ° Z E= Z F,求证：Z 1 = Z 2.30.已知：如图，Z 1 = Z 2,Z A= Z F，则Z C与Z D相等吗？试说明理由.31.如图，在四边形 ABCD 中，/ A= / C=90 ° / 1= / 2 / 3= / 4，求证：BE // DF .3C BCC BD334 .如图，已知/ 1 = / 2，/ C= / CDO ，求证：CD // OP .32.如图，已知/ 仁/2 求证：a // b35.如图，已知 DE 平分/ BDF , AF 平分/ BAC ，且 / 仁 / 2.求证(1) DF // AC ; (2) DE // AF .33.如图，DE 丄AO 于E , BO 丄AO 于O , FC 丄AB 于 C ,Z 仁/ 2,找出图中互相平行的线，并加以说明.36.如图，AD 平分/ BAC , EF 平分/ DEC ,且/ 1 = / 2 试说明DE 与AB 的位置关系.OO B37. 如图，在△ ABC中，点D在AB上，/ ACD= / A , /BDC的平分线交BC于点E.40.如图，直线AB、CD被直线EF所截，/ 1+ / 4=180° 求证：AB // CD .38. 如图，AB与CD相交于点0,并且/ A= / 1,试问 / 2与/B满足什么关系时，AC // BD ?说明理由.41 •如图所示，已知：/ 1 = / 2，/ E= / F.试说明AB // CD .39. 如图，已知/ 1 = / A，/ 2= / B,那么MN 与EF平行吗？如果平行，请说明理由.42 .如图，已知EF 丄CD 于F,/ GEF=25 ° / 1=65° 则AB与CD平行吗？请说明理由.求证：DE // AC .43.如图，已知/ 1= / 2=90° / 3=30° / 4=60 ° 图中有几对平行线？说说你的理由.46. 如图，已知B、C、D三点在同一条直线上， / B= / 1 , /2= / E,试说明AD // CE.44 .直线AB , CD被直线EF所截，/ 1 = 7 2，直线AB 和CD平行吗？为什么？F47. 直线AB、CD与GH交于E、F, EM平分/ BEF , FN 平分/ DFH , 7 BEF= 7 DFH , 求证：EM // FN .45.已知：如图，AD丄BC , EF丄BC ,7 1 = 7 2 .求证: AB// GF.48. 女口图所示，7 ABC= 7 BCD , BE、CF 分另U平分7 ABC和7 BCD，请你说出BE与CF的位置关系，并说出你的理由.C49. 如图，若/ 1= / 2,请判断DB与EC的位置关系, 并说明理由.52. 已知：如图，/ C= / 1，/ 2和/D互余，BE丄FD 于点G .求证：AB // CD.50. 如图，在△ ABC中，CD丄AB，垂足为D，点E在BC上，EF丄AB，垂足为F.(1)CD与EF平行吗？为什么？(2)如果/ 1 = / 2, DG // BC吗？为什么？53. 女口图，直线AB , CD 被EF 所截，/ 3= / 4, / 1 = 7 2,EG 丄FG.求证：AB // CD .51. 如图，已知：HG平分/ AHM , MN平分/ DMH , 且/AHM= 7 DMH .问：GH与MN有怎样的位置关系，请说明理由.(请注明每一步的理由)54. 已知：如图，CD是直线，E在直线CD上，7仁130°7 A=50 ° 求证：AB // CD .55. 如图，已知/ 仁/2, / DAB= / DCA ,且 DE 丄AC , 58. 如图，AD 丄BC 于点D ，/仁2,/ CDG= / B ,请 你判断EF与BC 的位置关系，并加以证明，要求写出 每步证明的理由.C56. 如图，四边形 ABCD , / 仁30 ° / B=60 ° AB 丄AC , 则AD 与BC 一定平行吗？ 理由，反之则不用说明理由. 59. 已知：如图， CE 平分/ ACD , / 1 = / B ,求证:AB // CE .AB 与CD 呢？若平行请说明ADBF 丄AC ，问：(1) AD // BC 吗？ (2) AB // CD 吗？为什么?D57.已知：如图，/ 求证：BD // CE .A= / F, / C= / D . 60.如图，已知/ 1 = / 2,/ 3= / 4,可以判定哪两条直。