下面是一张一种可变生产要素的短期生产函数的产量表

(完整word版)第四章生产者行为理论习题亲爱的读者：本文内容由我和我的同事精心收集整理后编辑发布到文库，发布之前我们对文中内容进行详细的校对，但难免会有错误的地方，如果有错误的地方请您评论区留言，我们予以纠正，如果本文档对您有帮助，请您下载收藏以便随时调用。

下面是本文详细内容。

最后最您生活愉快 ~O(∩_∩)O ~第四章生产者行为理论习题一、概念固定投入可变投入生产函数技术系数边际报酬递减规律等产量曲线边际技术替代率等成本线等斜线扩展线二、选择题：1.如果连续地增加某种生产要素，在总产量达到最大值的时候，边际产量曲线与（）A.平均产量曲线相交。

B.纵轴相交。

C.横轴相交。

2.当生产函数Q=f(L,K0)的AP L为正且递减时，MP L可以是：（）A.递减且为正；B.递减且为负C.为零D.上述任何一种情况3.在总产量、平均产量和边际产量的变化过程中（）A.边际产量的下降首先发生。

B.平均产量的下降首先发生。

C.总产量的下降首先发生。

4.边际收益递减规律发生作用的前提条件是（）A.连续地投入某种生产要素而保持其他生产要素不变。

B.按比例同时增加各种生产要素。

C.不按比例同时增加各种生产要素。

5.在边际收益递减规律的作用下，边际产量会发生递减。

此情况下，如果要产出同样数量的产品，应该（） A.停止增加变动的生产要素。

B.减少变动的生产要素的投入量。

C.增加变动的生产要素的投入量。

6.规模收益递减是在下述情况下发生的（）A. 连续地投入某种生产要素而保持其他生产要素不变B. 按比例连续增加各种生产要素C. 不按比例连续增加各种生产要素D.上述都正确7.如果规模收益不变，单位时间里增加了10%的劳动的使用，但保持资本量的不变，则产出将（）A.增加10%B.减少10%C.增加大于10%D.增加小于10%8.等成本曲线向外平行移动表明（）A. 产量提高了。

B.成本增加了。

C.生产要素的价格按相同比例上升了。

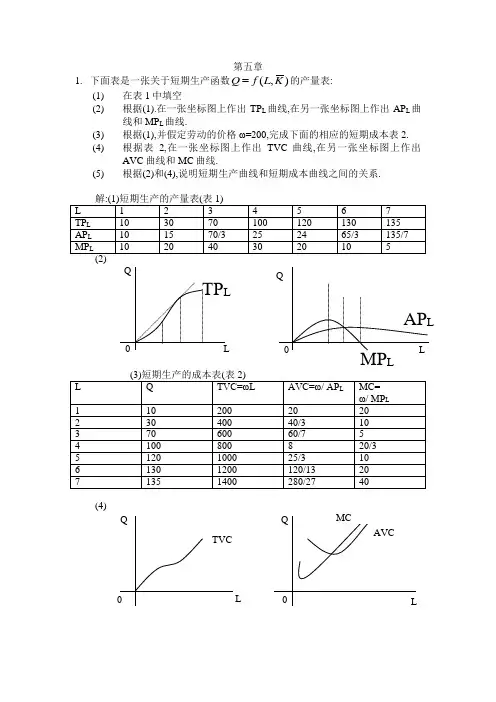
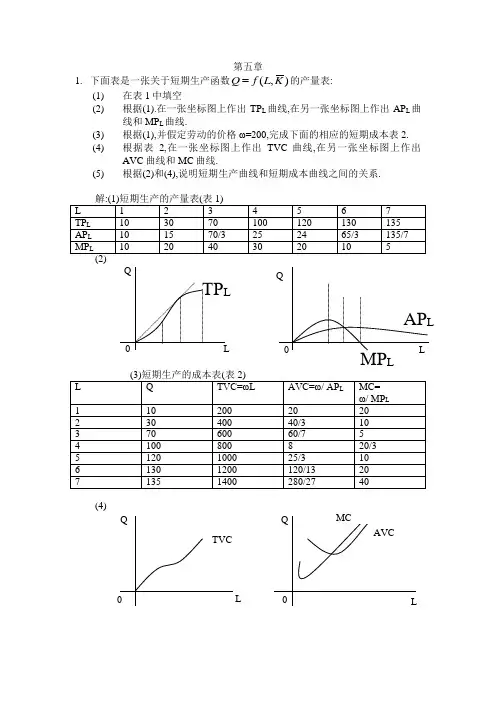
第五章1. 下面表是一张关于短期生产函数),(K L f Q 的产量表:(1) 在表1中填空 (2) 根据(1).在一张坐标图上作出TP L 曲线,在另一张坐标图上作出AP L 曲线和MP L 曲线.(3) 根据(1),并假定劳动的价格ω=200,完成下面的相应的短期成本表2. (4) 根据表2,在一张坐标图上作出TVC 曲线,在另一张坐标图上作出AVC 曲线和MC 曲线.(5) 根据(2)和(4),说明短期生产曲线和短期成本曲线之间的关系.(4)(5)边际产量和边际成本的关系,边际MC 和边际产量MP L 两者的变动方向是相反的.总产量和总成本之间也存在着对应系:当总产量TP L 下凸时,总成本TC 曲线和总可变成本TVC 是下凹的;当总产量曲线存在一个拐点时, 总成本TC 曲线和总可变成本TVC 也各存在一个拐点.平均可变成本和平均产量两者的变动方向是相反的.MC 曲线和AVC 曲线的交点与MP L 曲线和AP L 曲线的交点是对应的.2.下图是一张某厂商的LAC 曲线和LMC 曲线图.请分别在Q1和Q2的产量上画出代表最优生产规模的SAC 曲线和SMC 曲线.解:在产量Q1和Q2上,代表最优生产规模的SAC 曲线和SMC 曲线是SAC 1和SAC 2以及SMC 1和SMC 2. SAC 1和SAC 2分别相切于LAC 的A 和B SMC 1和SMC 2则分别相交于LMC 的A 1和B 1.3.假定某企业的短期成本函数是TC(Q)=Q 3-5Q 2+15Q+66: (1) 指出该短期成本函数中的可变成本部分和不变成本部分; (2) 写出下列相应的函数:TVC(Q)AC(Q)AVC(Q) AFC(Q)和MC(Q). 解(1)可变成本部分: Q 3-5Q 2+15Q不可变成本部分:66 (2)TVC(Q)= Q 3-5Q 2+15Q AC(Q)=Q 2-5Q+15+66/Q AVC(Q)= Q 2-5Q+15 AFC(Q)=66/Q MC(Q)= 3Q 2-10Q+15OMCQLMCSMC 1SAC 1SAC 2SMC 2 LACA 1B 1Q 1 Q 2长期边际成本曲线与短期成本曲线A4已知某企业的短期总成本函数是STC(Q)=0.04 Q 3-0.8Q 2+10Q+5,求最小的平均可变成本值.解: TVC(Q)=0.04 Q 3-0.8Q 2+10Q AVC(Q)= 0.04Q 2-0.8Q+10 令08.008.0=-='Q C AV 得Q=10又因为008.0>=''C AV 所以当Q=10时,6=MIN AVC5.假定某厂商的边际成本函数MC=3Q 2-30Q+100,且生产10单位产量时的总成本为1000.求:(1) 固定成本的值.(2)总成本函数,总可变成本函数,以及平均成本函数,平均可变成本函数. 解:MC= 3Q 2-30Q+100所以TC(Q)=Q 3-15Q 2+100Q+M 当Q=10时,TC=1000 ，所以有： 32101510100101000TC a =-⨯+⨯+= 解得 a =500即总固定成本TFC=500.（2）由（1），可得：TC(Q)=Q 3-15Q 2+100Q+500TVC(Q)= Q 3-15Q 2+100Q AC(Q)= Q 2-15Q+100+500/Q AVC(Q)= Q 2-15Q+1006.某公司用两个工厂生产一种产品,其总成本函数为C=2Q 12+Q 22-Q 1Q 2,其中Q 1表示第一个工厂生产的产量,Q 2表示第二个工厂生产的产量.求:当公司生产的总产量为40时能够使得公司生产成本最小的两工厂的产量组合. 解:构造F(Q)=2Q 12+Q 22-Q 1Q 2+λ(Q 1+ Q 2-40)令⎪⎩⎪⎨⎧-===⇒⎪⎪⎪⎭⎪⎪⎪⎬⎫=-+=∂∂=+-=∂∂=+-=∂∂3525150400204Q 2121122211λλλλQ Q Q Q FQ Q Q F Q Q F 使成本最小的产量组合为Q 1=15,Q 2=257已知生产函数Q=A 1/4L 1/4K 1/2;各要素价格分别为P A =1,P L =1.P K =2;假定厂商处于短期生产,且16=k .推导:该厂商短期生产的总成本函数和平均成本函数;总可变成本函数和平均可变函数;边际成本函数.)2(111)1(4,16:4/34/14/14/34/34/14/14/34/14/1A L P P L A L A LQ A QMP MP L A L QMP L A A QMP L A Q K L A L A LA =====∂∂∂∂==∂∂==∂∂===----所以所以因为解 由(1)(2)可知L=A=Q 2/16又TC(Q)=P A &A(Q)+P L &L(Q)+P K &16 = Q 2/16+ Q 2/16+32 = Q 2/8+32AC(Q)=Q/8+32/Q TVC(Q)= Q 2/8 AVC(Q)= Q/8 MC= Q/48已知某厂商的生产函数为Q=0.5L 1/3K 2/3;当资本投入量K=50时资本的总价格为500;劳动的价格P L =5,求: (1) 劳动的投入函数L=L(Q). (2) 总成本函数,平均成本函数和边际成本函数.当产品的价格P=100时,厂商获得最大利润的产量和利润各是多少? 解:(1)当K=50时，P K ·K=P K ·50=500,所以P K =10. MP L =1/6L -2/3K 2/3 MP K =2/6L 1/3K -1/310562613/13/13/23/2===--K L KL P P K L KL MP MP整理得K/L=1/1,即K=L.将其代入Q=0.5L 1/3K 2/3,可得:L(Q)=2Q（2）STC=ω·L （Q ）+r·50 =5·2Q+500 =10Q +500 SAC= 10+500/Q SMC=10（3）由(1)可知,K=L,且已知K=50,所以.有L=50.代入Q=0.5L 1/3K 2/3, 有Q=25. 又π=TR -STC =100Q-10Q-500 =1750所以利润最大化时的 产量Q=25,利润π=17509.假定某厂商短期生产的边际成本函数为SMC(Q)=3Q 2-8Q+100,且已知当产量Q=10时的总成本STC=2400，求相应的STC 函数、SAC 函数和AVC 函数。

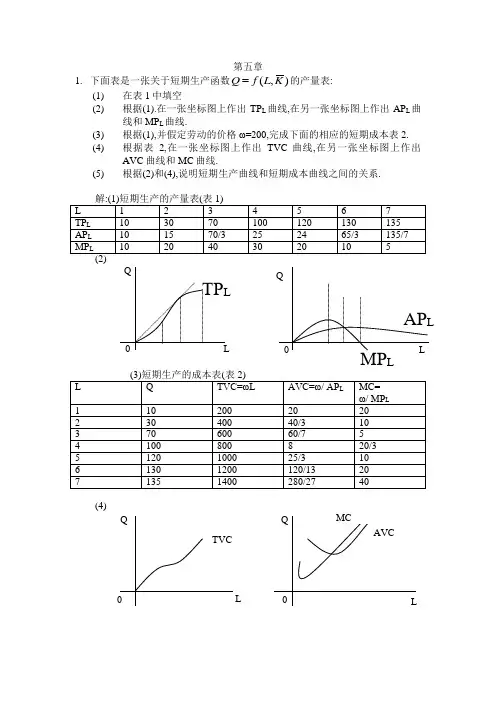
第五章1. 下面表是一张关于短期生产函数),(K L f Q 的产量表:(1) 在表1中填空 (2) 根据(1).在一张坐标图上作出TP L 曲线,在另一张坐标图上作出AP L 曲线和MP L 曲线.(3) 根据(1),并假定劳动的价格ω=200,完成下面的相应的短期成本表2. (4) 根据表2,在一张坐标图上作出TVC 曲线,在另一张坐标图上作出AVC 曲线和MC 曲线.(5) 根据(2)和(4),说明短期生产曲线和短期成本曲线之间的关系.(4)(5)边际产量和边际成本的关系,边际MC 和边际产量MP L 两者的变动方向是相反的.总产量和总成本之间也存在着对应系:当总产量TP L 下凸时,总成本TC 曲线和总可变成本TVC 是下凹的;当总产量曲线存在一个拐点时, 总成本TC 曲线和总可变成本TVC 也各存在一个拐点.平均可变成本和平均产量两者的变动方向是相反的.MC 曲线和AVC 曲线的交点与MP L 曲线和AP L 曲线的交点是对应的.2.下图是一张某厂商的LAC 曲线和LMC 曲线图.请分别在Q1和Q2的产量上画出代表最优生产规模的SAC 曲线和SMC 曲线.解:在产量Q1和Q2上,代表最优生产规模的SAC 曲线和SMC 曲线是SAC 1和SAC 2以及SMC 1和SMC 2. SAC 1和SAC 2分别相切于LAC 的A 和B SMC 1和SMC 2则分别相交于LMC 的A 1和B 1.3.假定某企业的短期成本函数是TC(Q)=Q 3-5Q 2+15Q+66: (1) 指出该短期成本函数中的可变成本部分和不变成本部分; (2) 写出下列相应的函数:TVC(Q)AC(Q)AVC(Q) AFC(Q)和MC(Q). 解(1)可变成本部分: Q 3-5Q 2+15Q不可变成本部分:66 (2)TVC(Q)= Q 3-5Q 2+15Q AC(Q)=Q 2-5Q+15+66/Q AVC(Q)= Q 2-5Q+15 AFC(Q)=66/Q MC(Q)= 3Q 2-10Q+15OMCQLMCSMC 1SAC 1SAC 2SMC 2 LACA 1B 1Q 1Q 2长期边际成本曲线与短期成本曲线A4已知某企业的短期总成本函数是STC(Q)=0.04 Q 3-0.8Q 2+10Q+5,求最小的平均可变成本值.解: TVC(Q)=0.04 Q 3-0.8Q 2+10Q AVC(Q)= 0.04Q 2-0.8Q+10 令08.008.0=-='Q C AV 得Q=10又因为008.0>=''C AV 所以当Q=10时,6=MIN AVC 5.假定某厂商的边际成本函数MC=3Q 2-30Q+100,且生产10单位产量时的总成本为1000.求:(1) 固定成本的值.(2)总成本函数,总可变成本函数,以及平均成本函数,平均可变成本函数. 解:MC= 3Q 2-30Q+100所以TC(Q)=Q 3-15Q 2+100Q+M 当Q=10时,TC=1000 ，所以有： 32101510100101000TC a =-⨯+⨯+= 解得 a =500即总固定成本TFC=500.（2）由（1），可得：TC(Q)=Q 3-15Q 2+100Q+500TVC(Q)= Q 3-15Q 2+100Q AC(Q)= Q 2-15Q+100+500/Q AVC(Q)= Q 2-15Q+1006.某公司用两个工厂生产一种产品,其总成本函数为C=2Q 12+Q 22-Q 1Q 2,其中Q 1表示第一个工厂生产的产量,Q 2表示第二个工厂生产的产量.求:当公司生产的总产量为40时能够使得公司生产成本最小的两工厂的产量组合. 解:构造F(Q)=2Q 12+Q 22-Q 1Q 2+λ(Q 1+ Q 2-40)令⎪⎩⎪⎨⎧-===⇒⎪⎪⎪⎭⎪⎪⎪⎬⎫=-+=∂∂=+-=∂∂=+-=∂∂3525150400204Q 2121122211λλλλQ Q Q Q FQ Q Q F Q Q F 使成本最小的产量组合为Q 1=15,Q 2=257已知生产函数Q=A 1/4L 1/4K 1/2;各要素价格分别为P A =1,P L =1.P K =2;假定厂商处于短期生产,且16=k .推导:该厂商短期生产的总成本函数和平均成本函数;总可变成本函数和平均可变函数;边际成本函数.)2(111)1(4,16:4/34/14/14/34/34/14/14/34/14/1A L P P L A L A LQ A QMP MP L A L QMP L A A QMP L A Q K L A L A LA =====∂∂∂∂==∂∂==∂∂===----所以所以因为解 由(1)(2)可知L=A=Q 2/16又TC(Q)=P A &A(Q)+P L &L(Q)+P K &16 = Q 2/16+ Q 2/16+32 = Q 2/8+32AC(Q)=Q/8+32/Q TVC(Q)= Q 2/8 AVC(Q)= Q/8 MC= Q/48已知某厂商的生产函数为Q=0.5L 1/3K 2/3;当资本投入量K=50时资本的总价格为500;劳动的价格P L =5,求: (1) 劳动的投入函数L=L(Q). (2) 总成本函数,平均成本函数和边际成本函数.当产品的价格P=100时,厂商获得最大利润的产量和利润各是多少? 解:(1)当K=50时，P K ·K=P K ·50=500,所以P K =10. MP L =1/6L -2/3K 2/3 MP K =2/6L 1/3K -1/310562613/13/13/23/2===--K L KL P P K L KL MP MP整理得K/L=1/1,即K=L.将其代入Q=0.5L 1/3K 2/3,可得:L(Q)=2Q（2）STC=ω·L （Q ）+r·50 =5·2Q+500 =10Q +500 SAC= 10+500/Q SMC=10（3）由(1)可知,K=L,且已知K=50,所以.有L=50.代入Q=0.5L 1/3K 2/3, 有Q=25. 又π=TR -STC =100Q-10Q-500 =1750所以利润最大化时的 产量Q=25,利润π=17509.假定某厂商短期生产的边际成本函数为SMC(Q)=3Q 2-8Q+100,且已知当产量Q=10时的总成本STC=2400，求相应的STC 函数、SAC 函数和AVC 函数。

第四章生产者选择（1）一、选择题1、边际收益递减规律发生作用的前提是（ D ）A．存在技术进步B．生产技术水平不变C．只有一种可变要素的生产D．B与C2、当边际产量大于平均产量时，（ A ）A．平均产量增加B．平均产量减少C．平均产量不变D．平均产量达到最低点3、在规模报酬不变阶段，若劳动的使用量增加10%，资本的使用量不变，则（ D ）A．产出增加10% B．产出减少10% C．产出的增加大于10% D．产出的增加小于10%4、当劳动的（L）总产量下降时，（ C ）A/劳动的平均产量为负B劳动的平均产量为零C劳动的边际产量为负D劳动的边际产量为零5、当劳动的平均产量为正但递减时，劳动的边际产量是（ D ）A正 B 零C负D以上情况都有可能6、下列说法中错误的一种说法是（ B ）A只要总产量减少，边际产量一定是负数B只要边际产量减少，总产量一定也减少C随着某种生产要素投入量的增加，边际产量和平均产量增加到一定程度将趋于下降D边际产量曲线一定在平均产量曲线的最高点与之相交7、当劳动L的边际产量为负时，我们是处于（ C ）A L的第一阶段B L的第二阶段C 的第三阶段D 上述都不是8、等产量曲线是指在这条曲线上的各点代表（D ）A．为生产同等产量投入要素的各种组合比例是不能变化的B．为生产同等产量投入要素的价格是不变的C．不管投入各种要素量如何，产量总是相等的D．投入要素的各种组合所能生产的产量都是相等的9、如果连续地增加某种生产要素，在总产量达到最大时，边际产量曲线（ D ）A. 与纵轴相交B. 经过原点C. 与平均产量曲线相交D. 与横轴相交10、如果等成本线与等产量线没有交点，那么要生产等产量曲线所表示的产量，应该（B ）A. 增加投入B. 保持原投入不变C. 减少投入D. 上述均不正确11、等成本曲线围绕着它与纵轴（Y）的交点逆时针移动表明（ C ）A生产要素Y的价格上升了B生产要素X的价格上升了C生产要素X的价格下降了D生产要素Y的价格下降了四、分析讨论题1、已知生产函数Q=AL1/3K2/3，判断：（1）在短期生产中，该生产函数是否受边际报酬递减规律支配？（提示判断dMP/dL 的值是大于零还是小于零）（2）长期属于规模报酬的哪一种类型？解：（1）因为Q=F(L、K)=AL1/3K2/3，于是有：F(tL、tK)= A(tL)1/3(tK)2/3=t·F(L、K)所以，生产函数Q=AL1/3K2/3属于规模报酬不变的生产函数。

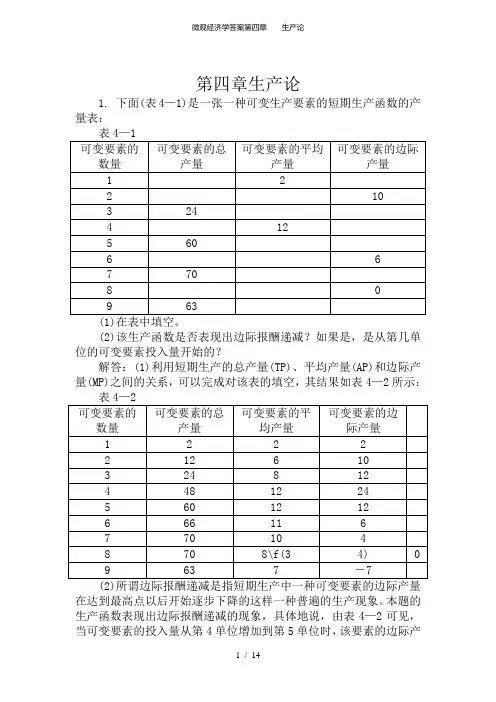
第四章生产论1. 下面(表4—1)是一张一种可变生产要素的短期生产函数的产量表：表4—1(2)该生产函数是否表现出边际报酬递减？如果是，是从第几单位的可变要素投入量开始的？解答：(1)利用短期生产的总产量(TP)、平均产量(AP)和边际产量(MP)之间的关系，可以完成对该表的填空，其结果如表4—2所示：在达到最高点以后开始逐步下降的这样一种普遍的生产现象。

本题的生产函数表现出边际报酬递减的现象，具体地说，由表4—2可见，当可变要素的投入量从第4单位增加到第5单位时，该要素的边际产量由原来的24下降为12。

2.用图说明短期生产函数Q ＝f(L ，K －)的TP L 曲线、AP L 曲线和MP L曲线的特征及其相互之间的关系。

解答：短期生产函数的TP L 曲线、AP L 曲线和MP L 曲线的综合图如图4—1所示。

图4—1由图4—1可见，在短期生产的边际报酬递减规律的作用下，MP L曲线呈现出先上升达到最高点A 以后又下降的趋势。

从边际报酬递减规律决定的MP L 曲线出发，可以方便地推导出TP L 曲线和AP L 曲线，并掌握它们各自的特征及相互之间的关系。

关于TP L 曲线。

由于MP L ＝d TP Ld L，所以，当MP L ＞0时，TP L 曲线是上升的；当MP L ＜0时，TP L 曲线是下降的；而当MP L ＝0时，TP L 曲线达最高点。

换言之，在L ＝L 3时，MP L 曲线达到零值的B 点与TP L 曲线达到最大值的B′点是相互对应的。

此外，在L ＜L 3即MP L ＞0的范围内，当MP′L ＞0时，TP L 曲线的斜率递增，即TP L 曲线以递增的速率上升；当MP′L ＜0时，TP L 曲线的斜率递减，即TP L 曲线以递减的速率上升；而当MP′＝0时，TP L 曲线存在一个拐点，换言之，在L ＝L 1时，MP L 曲线斜率为零的A 点与TP L 曲线的拐点A′是相互对应的。

关于AP L 曲线。

第四章生产函数一、简答题1.如何准确区分生产的短期和长期这两个基本概念?2.下面是一张一种可变生产要素的短期生产函数的产量表（表４—１）：（１）在表中填空。

（２）该生产函数是否表现出边际报酬递减？如果是，是从第几单位的可变要素投入量开始的？—3．区分边际报酬递增、不变和递减的情况与规模报酬递增、不变和递减的情况。

4.假设生产函数Q＝min{5L,2K}。

(1)作出Q＝50时的等产量曲线。

(2)推导该生产函数的边际技术替代率函数。

(3)分析该生产函数的规模报酬情况。

5.已知柯布道格拉斯生产函数为Q＝ALαKβ。

请讨论该生产函数的规模报酬情况。

二、计算题1.已知生产函数Q＝f(L，K)=2KL- 0.5L2-0.5K2，假定厂商目前处于短期生产，且K＝10，求：(1)写出在短期生产中该厂商关于劳动的总产量TP L 函数、劳动的平均产量AP L 函数和劳动的边际产量MP L 函数。

(2)分别计算当总产量TP L 、劳动平均产量AP L 和劳动边际产量MP L 各自达到极大值时的厂商劳动的投入量。

(3)什么时候AP L ＝MP L ？它的值又是多少？2．已知生产函数为Q ＝min(K L 3,2)。

求：（1）当Q ＝36时，L 与K 值分别是多少？（2）如果生产要素的价格分别为L P =2，K P =5，则生产480单位产量时的最小成本是多少？3.假设某厂商的短期生产函数为 Q ＝35L ＋8L 2－L 3。

求：(1)该企业的平均产量函数和边际产量函数。

(2)如果企业使用的生产要素的数量为L ＝6，是否处理短期生产的合理区间？为什么？5．令生产函数f （L ，K ）=a 0＋a 1(LK)1/2＋a 2K ＋a 3L ，其中0≤a i ≤1 i=0，1，2，3。

（1）当满足什么条件时，该生产函数表现出规模报酬不变的特征。

（2）证明：在规模报酬不变的情况下，相应的边际产量是递减的。

三、论述题用图说明短期生产函数Q ＝f(L ，k )的TP L 曲线，AP L 曲线和MP L 曲线的特征及其相互之间的关系。

第五章1. 下面表是一张关于短期生产函数),(K L f Q 的产量表:(1) 在表1中填空 (2) 根据(1).在一张坐标图上作出TP L 曲线,在另一张坐标图上作出AP L 曲线和MP L 曲线.(3) 根据(1),并假定劳动的价格ω=200,完成下面的相应的短期成本表2. (4) 根据表2,在一张坐标图上作出TVC 曲线,在另一张坐标图上作出AVC 曲线和MC 曲线.(5) 根据(2)和(4),说明短期生产曲线和短期成本曲线之间的关系.(5)边际产量和边际成本的关系,边际MC 和边际产量MP L 两者的变动方向是相反的.总产量和总成本之间也存在着对应系:当总产量TP L 下凸时,总成本TC 曲线和总可变成本TVC 是下凹的;当总产量曲线存在一个拐点时, 总成本TC 曲线和总可变成本TVC 也各存在一个拐点.平均可变成本和平均产量两者的变动方向是相反的.MC 曲线和AVC 曲线的交点与MP L 曲线和AP L 曲线的交点是对应的.2.下图是一张某厂商的LAC 曲线和LMC 曲线图.请分别在Q1和Q2的产量上画出代表最优生产规模的SAC 曲线和SMC 曲线.解:在产量Q1和Q2上,代表最优生产规模的SAC 曲线和SMC 曲线是SAC 1和SAC 2以及SMC 1和SMC 2. SAC 1和SAC 2分别相切于LAC 的A 和B SMC 1和SMC 2则分别相交于LMC 的A 1和B 1.3.假定某企业的短期成本函数是TC(Q)=Q 3-5Q 2+15Q+66: (1) 指出该短期成本函数中的可变成本部分和不变成本部分; (2) 写出下列相应的函数:TVC(Q)AC(Q)AVC(Q) AFC(Q)和MC(Q).解(1)可变成本部分: Q 3-5Q 2+15Q不可变成本部分:66 (2)TVC(Q)= Q 3-5Q 2+15Q AC(Q)=Q 2-5Q+15+66/Q AVC(Q)= Q 2-5Q+15 AFC(Q)=66/Q MC(Q)= 3Q 2-10Q+15OMCQLMCSMC 1SAC 1SAC 2SMC 2 LACA 1B 1Q 1 Q 2长期边际成本曲线与短期成本曲线A4已知某企业的短期总成本函数是STC(Q)=0.04 Q 3-0.8Q 2+10Q+5,求最小的平均可变成本值.解: TVC(Q)=0.04 Q 3-0.8Q 2+10Q AVC(Q)= 0.04Q 2-0.8Q+10 令08.008.0=-='Q C AV 得Q=10又因为008.0>=''C AV 所以当Q=10时,6=MINAVC5.假定某厂商的边际成本函数MC=3Q 2-30Q+100,且生产10单位产量时的总成本为1000.求:(1) 固定成本的值.(2)总成本函数,总可变成本函数,以及平均成本函数,平均可变成本函数. 解:MC= 3Q 2-30Q+100所以TC(Q)=Q 3-15Q 2+100Q+M 当Q=10时,TC=1000 ，所以有：32101510100101000TC a =-⨯+⨯+= 解得 a =500即总固定成本TFC=500.（2）由（1），可得：TC(Q)=Q 3-15Q 2+100Q+500TVC(Q)= Q 3-15Q 2+100Q AC(Q)= Q 2-15Q+100+500/Q AVC(Q)= Q 2-15Q+1006.某公司用两个工厂生产一种产品,其总成本函数为C=2Q 12+Q 22-Q 1Q 2,其中Q 1表示第一个工厂生产的产量,Q 2表示第二个工厂生产的产量.求:当公司生产的总产量为40时能够使得公司生产成本最小的两工厂的产量组合. 解:构造F(Q)=2Q 12+Q 22-Q 1Q 2+λ(Q 1+ Q 2-40)令⎪⎩⎪⎨⎧-===⇒⎪⎪⎪⎭⎪⎪⎪⎬⎫=-+=∂∂=+-=∂∂=+-=∂∂3525150400204Q 2121122211λλλλQ Q Q Q FQ Q Q F Q Q F使成本最小的产量组合为Q 1=15,Q 2=257已知生产函数Q=A 1/4L 1/4K 1/2;各要素价格分别为P A =1,P L =1.P K =2;假定厂商处于短期生产,且16=k .推导:该厂商短期生产的总成本函数和平均成本函数;总可变成本函数和平均可变函数;边际成本函数.)2(111)1(4,16:4/34/14/14/34/34/14/14/34/14/1A L P P L A L A LQ A QMP MP LAL Q MP LA A Q MP LA Q K L A LA L A =====∂∂∂∂==∂∂==∂∂===----所以所以因为解由(1)(2)可知L=A=Q 2/16又TC(Q)=P A &A(Q)+P L &L(Q)+P K &16 = Q 2/16+ Q 2/16+32 = Q 2/8+32AC(Q)=Q/8+32/Q TVC(Q)= Q 2/8 AVC(Q)= Q/8 MC= Q/48已知某厂商的生产函数为Q=0.5L 1/3K 2/3;当资本投入量K=50时资本的总价格为500;劳动的价格P L =5,求: (1) 劳动的投入函数L=L(Q). (2) 总成本函数,平均成本函数和边际成本函数.当产品的价格P=100时,厂商获得最大利润的产量和利润各是多少? 解:(1)当K=50时，P K ·K=P K ·50=500,所以P K =10. MP L =1/6L -2/3K 2/3 MP K =2/6L 1/3K -1/310562613/13/13/23/2===--KL KL P P KLKLMP MP整理得K/L=1/1,即K=L.将其代入Q=0.5L 1/3K 2/3,可得:L(Q)=2Q（2）STC=ω·L （Q ）+r·50 =5·2Q+500 =10Q +500 SAC= 10+500/Q SMC=10（3）由(1)可知,K=L,且已知K=50,所以.有L=50.代入Q=0.5L 1/3K 2/3, 有Q=25. 又π=TR -STC =100Q-10Q-500 =1750所以利润最大化时的 产量Q=25,利润π=17509.假定某厂商短期生产的边际成本函数为SMC(Q)=3Q 2-8Q+100,且已知当产量Q=10时的总成本STC=2400，求相应的STC 函数、SAC 函数和AVC 函数。

第四章生产函数第一部分教材配套习题本习题详解一、简答题1.如何准确区分生产的短期和长期这两个基本概念生产的短期：指生产者来不及调整全部生产要素的数量，至少有一种生产要素的数量是固定不变的时间周期。

短期不可调整的生产要素称不变生产要素，一般包括厂房、大型设备、高级管理者、长期贷款等，可调整的生产要素成为可变生产要素，一般包括原材料、燃料、辅助材料、普通劳动者等。

生产的长期：指生产者可以调整全部生产要素的数量的时间周期。

生产的短期和长期是相对的时间概念,不是绝对的时间概念，其与企业所属行业、所用技术设备和规模等因素有关。

2.下面是一张一种可变生产要素的短期生产函数的产量表（表４—１）：（１）在表中填空。

（２）该生产函数是否表现出边际报酬递减如果是，是从第几单位的可变要素投入量开始的表４—１解答：（１）在表４—１中填空得到表４—２。

表４—２3．区分边际报酬递增、不变和递减的情况与规模报酬递增、不变和递减的情况。

解答：边际报酬变化是指在生产过程中一种可变要素投入量每增加一个单位时所引起的总产量的变化量，即边际产量的变化，而其他生产要素均为固定生产要素，固定要素的投入数量是保持不变的。

边际报酬变化一般包括边际报酬递增、不变和递减三个阶段。

很显然，边际报酬分析可视为短期生产分析。

规模报酬分析方法是描述在生产过程中全部生产要素的投入数量均同比例变化时所引起的产量变化特征，当产量的变化比例分别大于、等于、小于全部生产要素投入量变化比例时，则分别为规模报酬递增、不变、递减。

很显然，规模报酬分析可视为长期生产的分析视角。

区别：①前提条件不同，边际报酬变化生产要素分为不变和可变生产要素，生产要素比例发生变化；规模报酬分析研究生产要素同比例变动。

②考察时间长短不同。

边际报酬变化分析的是短期生产规律；规模报酬研究长期生产规律。

③指导意义不同。

边际报酬变化指出要按比例配置生产要素；规模报酬指出要保持企业的适度规模。

④由于前提条件不同，两规律独立发挥作用，不存在互为前提，互为影响关系。

第一章作业题一、单选1.供给的变动引起（）。

A.均衡价格和均衡数量同方向变动B.均衡价格与均衡数量反方向变动C.均衡价格反方向变动，均衡数量同方向变动D.均衡价格同方向变动，均衡数量反方向变动2.政府为了扶植农业，对农产品实行支持价格。

但政府必须（）。

A.实行农产品配给制B.收购过剩的农产品C.增加对农产品的税收D.大量进口农产品3.政府为了扶植某一行业生产而规定的该行业的最低价格是（）A.限制价格B.支持价格C.领先价格D.歧视价格4.限制价格的运用会导致（）A.产品大量积压B.消费者随时可以购买到自己希望得到的产品C.供给增加D.黑市交易盛行5．需求的价格弹性是指（）。

A．需求函数的斜率B．收入变化对需求的影响程度C．消费者对价格变化的反映程度D．以上说法都正确6．假定某商品的价格从10美元下降到9美元，需求量从70增加到75，则需求为（）。

A．缺乏弹性B．富有弹性C．单位弹性D．难以确定7．某类电影现行平均票价为4元，对该类电影需求的价格弹性为－1.5，经常出现许多观众买不到票的现象，这些观众大约占可买到票的观众的15%，采取以下（）的方法，可以使所有想看电影而有能买得起票的观众都能买得到票。

A．电影票降价10%B．电影票提价15%C．电影票提价10%D．电影票降价15%8．下列（）情况使总收益增加。

A．价格上升，需求缺乏弹性B．价格下降，需求缺乏弹性C．价格上升，需求富有弹性D．价格下降，需求单位弹性二、判断1.牛奶的价格上涨，豆浆的需求量会上升（）2.胶卷的价格上涨，照相机的需求量会上升（）3.如果预期自行车的价格会上涨，则对它的需求量会下跌。

（）4.消费者A需要也愿意购买一台电脑，就构成对电脑的需求。

（）5. 一切商品和服务的需求曲线都是一条向右下方倾斜的、斜率为负值的曲线。

（）6.需求曲线向左平行移动，这表示需求减少。

（）7.供给曲线向右平行移动，这表示供给减少。

（）8.禽流感传播初期，鸡蛋的价格会上涨。

第四章生产函数第一部分教材配套习题本习题详解一、简答题1.如何准确区分生产的短期和长期这两个基本概念生产的短期：指生产者来不及调整全部生产要素的数量，至少有一种生产要素的数量是固定不变的时间周期。

短期不可调整的生产要素称不变生产要素，一般包括厂房、大型设备、高级管理者、长期贷款等，可调整的生产要素成为可变生产要素，一般包括原材料、燃料、辅助材料、普通劳动者等。

生产的长期：指生产者可以调整全部生产要素的数量的时间周期。

生产的短期和长期是相对的时间概念,不是绝对的时间概念，其与企业所属行业、所用技术设备和规模等因素有关。

|2.下面是一张一种可变生产要素的短期生产函数的产量表（表４—１）：（１）在表中填空。

（２）该生产函数是否表现出边际报酬递减如果是，是从第几单位的可变要素投入量开始的—解答：（１）在表４—１中填空得到表４—２。

·3．区分边际报酬递增、不变和递减的情况与规模报酬递增、不变和递减的情况。

解答：边际报酬变化是指在生产过程中一种可变要素投入量每增加一个单位时所引起的总产量的变化量，即边际产量的变化，而其他生产要素均为固定生产要素，固定要素的投入数量是保持不变的。

边际报酬变化一般包括边际报酬递增、不变和递减三个阶段。

很显然，边际报酬分析可视为短期生产分析。

规模报酬分析方法是描述在生产过程中全部生产要素的投入数量均同比例变化时所引起的产量变化特征，当产量的变化比例分别大于、等于、小于全部生产要素投入量变化比例时，则分别为规模报酬递增、不变、递减。

很显然，规模报酬分析可视为长期生产的分析视角。

区别：①前提条件不同，边际报酬变化生产要素分为不变和可变生产要素，生产要素比例发生变化；规模报酬分析研究生产要素同比例变动。

②考察时间长短不同。

边际报酬变化分析的是短期生产规律；规模报酬研究长期生产规律。

③指导意义不同。

边际报酬变化指出要按比例配置生产要素；规模报酬指出要保持企业的适度规模。

④由于前提条件不同，两规律独立发挥作用，不存在互为前提，互为影响关系。

微观经济学练习题均衡价格理论1、某市场的供给曲线与需求曲线分别为P=4Q s和P=12-2Q d;求出该市场的均衡价格和均衡数量;Q s =1/4P Q d=1/212-P Q s = Q d 1/4P=1/212-P P=8,Q=22、如果大豆是牛的一种饲料,那么对大豆市场的价格补贴计划会如何影响牛肉的均衡价格和均衡数量;价格补贴计划会抬高牛饲料的价格,这又会使牛肉的供给曲线向左上方移动;于是牛肉的均衡价格上涨,均衡数量减少;图略3、考虑一个市场,其供给曲线和需求曲线分别为：P=4Qs和P=12-2Qd;如果对场卖主出售的每单位产出课税为6,均衡价格和均衡数量将会受到什么影响如果对买主征收同样的税呢最初的均衡价格和均衡数量分别为：4Q s=12-2Q d,解出Q=2,P=8税后,供给曲线变为：P=6+4 Q s P′,Q′分别表示税后的均衡价格和均衡数量;得：=6+4Q′=12-2Q′,解出,P′=10,Q′=1P′代表买主支付的价格;P′-6=4是卖主收取的价格;若对买主课以6美元的税,则需求曲线变为P=6-2Q d,于是得到4Q″=6-2Q″,解出Q″=1,P″=4;P″代表卖主收取的价格;P″+T= P″+6=10是买主支付的价格;4、1986年7月某外国城市公共汽车票从32美分提高到40美分,同年8月的乘客为880万人次,与1985年同期相比减少了12%,求需求的价格弧弹性;解：P1=32 P2=40 Q2=880Q1=880/1－12%=1000E d= △Q/Q1+Q2· P1+P2 /△ P=880 －1000/40 －32×40+32/1000+880=-0.57所以,需求的价格弧弹性约为-0.575、X公司和Y公司是机床行业的两个竞争者,其主要产品的需求曲线分别为：PX=1000—5QX PY=1600—4QY这两家公司现在的销售量分别为100单位X和250单位Y;A：求X和Y当前的价格弹性;A：Q X=100 Q Y=250P X=1000－5Q X=1000 －5×100=500P Y=1600－4Q Y=1600 －4 ×250=600E dX=dQ X/dP X· P X/Q X=–1/5 ×500/100= –1E dY=dQ Y/dP Y· P Y/Q Y= –1/4 ×600/250 = –0.6B：假定Y降价以后,使Q Y增加到300单位;同时导致X销售量Q X下降到75单位;试问X公司产品X的交叉价格弹性是多少由题设Q Y=300 Q X=75 P Y=1600－4 Q Y=1600 －4 ×300=400△Q X=75 －100=-25 △P Y=400 －600=-200于是X对Y的交叉弹性为：E XY= -25/ -200 ×600+400/100+75=5/7C：假定Y公司目标是谋求销售收入极大,你认为它降价在经济上是否合理由A可知,Y公司生产的产品Y在价格P=600下的需求价格弹性为－0.6,也就是说其需求缺乏弹性,在这种情况下降低价格将减少其销售收入;验证如下：降价前,Y公司的销售收入为TR=600×250=150 000降价后,Y公司的销售收入为TR=400×300=120 000所以降价对Y公司在经济上是不合理的;在英国,对新汽车的需求价格弹性Ed= —1.2,需求收入弹性EY=3.0,试计算：A：其它条件不变,价格提高3%对需求的影响B：其它条件不变,收入增加2%对需求的影响C：如果价格提高8%,收入增加10%,1980年新汽车销售量为800万量,则1981年新汽车销售量为多少A：E d= dQ/Q·P/dP= dQ/Q ·1/3%=-1.2 dQ/Q=-3.6% 即价格提高3%使需求减少3.6% B： E Y= dQ/Q·Y/dY= dQ/Q ·1/2%=3 dQ/Q=6% 即收入增加2%使需求增加6%;C：价格提高8%时,使需求量减少 Q1=800×－1.2 ×8%收入增加10%时,使需求量增加 Q2=800×－3 ×10%于是1981年新汽车的销售量为Q=800+ Q1+ Q2=963.2万辆;消费者行为理论1、假定某消费者的收入M=100美元/周,全部花费在住房与食物上;如果住房价格P1=5美元/平方米,食物价格P2=10美元/磅;1请画出预算约束线;2如果住房价格由5美元/平方米下降到4美元/平方米,预算约束线如何变化3如果食物价格由10美元/磅涨到20美元/磅,预算约束线如何变化4如果住房价格住房价格由5美元/平方米上升到10美元/平方米,食物价格由10美元/磅涨到20美元/磅,预算约束线如何变化2、0.10美元/片,黄油价格是;那么他每个月可消费多少面包和黄油1 12=0.1X+0.2YX=2Y于是,X=24片面包月 Y=48片黄油/月2新的偏好是一片面包放一块黄油12=0.1X+0.2YX=Y于是,X=40片面包月 Y=40片黄油/月3、假设某消费者的均衡如下图;已知商品1的价格P1=2元X2 A：求消费者的收入20 B ：求商品2的价格I=P1X1+P2X2 C ：写出预算线方程,并求其斜率 100 X115 30A ： 当 P 1=2 X 1=30, 则I=60B ：P 2=60/20=3C ：2X 1+ 3X 2=60 其斜率为：20/-30=-2/34、已知某消费者每年用于商品1和商品2的收入为540元,两商品的价格分别为P1=20元和P2=30元;该消费者的效用函数为U=3X1X22,该消费者每年购买这两种商品的数量是多少每年从中得到的总效用是多少由题已知,20X 1+30X 2=540 U=3X 1X 22消费者均衡的条件为：MU 1 /P 1=MU 2 /P 2 即 3X 22/20=6X 1X 2/30 X 2=4/3X 1 20X 1+30X 2=540 X 2=4/3X 1X 1 =9 X 2= 12U=3×9×122=38885、假定某商品市场只有A 、B 两个消费者,他们的需求函数各自为QdA=20—4P,QdB=30—5P 1：列出这两个消费者的需求表和市场需求表2：根据1画出这两个消费者的需求曲线和市场需求曲线2图略6、若甲的效用函数为U=XY;1 X=40 Y=5时,他得到的效用是多少过点40,5的无差异曲线是什么2 若甲给予25单位X 的话, 愿给甲15单位Y,进行这种交换,甲所得到的满足会比40,5的组合高吗（3） 用15单位Y 同甲换取X,为使甲的满足与40,5组合相同,他最多只能得到多少单位X1当X=40,Y=5时,U=XY=200;过点40,5的无差异曲线是XY=200; 2 甲的商品组合为40,5,现在进行交换,甲得到15单位Y,失去25单位X,商品组合为15,20, 这时他的效用U=XY=300原来商品组合40,5提供的效用是200,现在交换后的商品组合15,20提供的效用是300,显然他的满足程度提高100;3 甲交换后的商品组合X,15+5所提供的满足程度与商品组合40,5提供的满足200相同时,他要放弃的X 量为： XY=X ×15+5=200 X=10,甲必须放弃40—10=30单位X也就是说最多只能得到30单位的X;把40元的收入有于购买两种商品A和B,PA=10元,PB=5元（1）写出预算方程2若把收入全部用于购买A,能买多少单位A3若把收入全部用于购买B,能买多少单位B 并画出预算线;4若收入下降为30元,两商品的价格都是5元,写出新的预算方程,并画出预算线;1 10A+5B=42 10A=40 A=43 5B=40 B=84 5A+5B=30 图略8、若某人用全部收入能购买4单位X和6单位Y,或者12单位X和2单位Y;1画出预算线 2商品X的价格与商品Y的价格之比是多少1预算线见图2P X·4+ P Y·6= P X·12+ P Y·2P X·8= P Y·4P X/ P Y=1/29、某大学生即将参加三门功课的期终考试,他能够用来复习功课的时间只有6小时;每门功课占用的时间和相应会有的成绩如下表：为了使这三门课的成绩总分最高,他应该怎样分配复习时间说明你的理由;从表中可知,经济学用3小时,数学用2小时,统计学用1小时,它们每小时的边际效用都是10分;而且所用总时间=3+2+1=6小时;注意：如果三门课分别用4、3、2小时,每小时的MU=8分,但总时间为9小时,大于6小时;10、假定某人将收入全部用于购买商品X和Y,其中PX=20元,PY=30元,收入为210元;（1）每种商品的消费量是多少 2 最大效用是多少（2）1当他购买X=3,Y=5时满足最大,因为,MU X/P X=20/20=1MU Y/P Y=30/30=1 而3×20+5×30=2102最大总效用=TU X+ TU Y=25+23+20+50+45+40+35+30 =26811、已知某人月收入120元,全部用于购买商品X 和Y,其效用函数为U=XY,PX=2元,PY=3元;（1）要使效用最大,该购买的X和Y各为多少（2）假如X的价格提高44%,Y的价格不变,为保持原有的效用水平,收入必须增加多少1由U=XY 得 MU X=Y MU Y=X于是 MU X/P X=MU Y/P Y即Y/2=X/3 又 2X+3Y=120Y/2=X/3可得 X=30 Y=202现在P X=2+2×44%=2.88MU X/P X=MU Y/P Y 即 Y/ 2.88=X/3 U=XY=60得 X=25 Y=24M=P X X+ P Y Y=2.88×25+3×24=144元△M=144－120=24元为保持原有的效用水平,必须增加收入24元;12、无差异曲线U=X0.4Y0.6=9 P X=2, P Y=3;1X、Y的均衡消费量 2效用等于9时的最小支出;1U=X0.4Y0.6 MU X=0.4X-0.6Y0.6 MU Y=0.6X0.4Y-0.4MU X/P X=MU Y/P Y 即 0.4X-0.6Y0.6 /2= 0.6X0.4Y-0.4 /3X0.4Y0.6=9 得X=Y=92效用等于9时的最小支出为：P X X+ P Y Y=2×9+3×9=45元生产理论1、下面是一张一种可变生产要素的短期生产函数的产量表：在表中填空该生产函数是否表现出边际报酬递减如果是,是从第几单位的可变生产要素投入量开始的是的, 该函数从第5单位可变生产要素投入量开始表现出边际报酬递减;2、已知某企业的生产函数为Q=L错误!K错误! ,劳动的价格w=2,资本的价格r=1;求：（1）当成本C=3000时,企业实现最大产量时的L、K和Q的均衡值;（2）当产量Q=800时,企业实现最小成本时的L、K和C的均衡值;1MP L=2/3L-1/3K1/3MP K =1/3L2/3K-2/3又MP L/P L= MP K/P K2/3L-1/3K1/3/2= 1/3L2/3K-2/3/1即K=L3000=2L+K L=K 得L=K=1000 Q=1000 2 由上可知L=K 则800=L=K TC=2L+K=24003、已知生产函数为Q=KL—0.5L2—0.32K2, 令上式K=10;（1）写出APPL函数和MPPL函数;（2）分别计算当TP、AP和MP达到极大值时厂商雇用的劳动;（3）证明当APPL达到极大时APPL=MPPL=21Q=KL－0.5L2 －0.32K2令K=10则Q=10L－0.5L2 －0.32×102 =－32+10L －0.5L2劳动的平均产量函数 APP L =Q/L=10 －0.5L －32/L劳动的边际产量函数 MPP L =dQ/dL=10－L2对于Q =－32+10L －0.5L2 ,求其最大值时,令MPP L =0即10－L =0 L=10又dQ/dL dQ/dL=-1﹤0 所求L=10为极大值;当总产量达到极大时厂商雇用的劳动为10;3由于 APP L =10－0.5L －32/L,当APP L达到最大时, APP L′=0即－0.5+32/L2=0L2=64 L=8负值舍去又APP L″=－64/L3﹤0,故L=8时为极大值;L=8时, APP L =10－0.5L －32/L=2MPP L=10－L=2故当APP L达到最大时, APP L= MPP L=24、已知生产函数为Q=K0.5L0.5,试证明：（1）该生产过程是规模报酬不变;（2）受报酬递减规律的支配1证明：Q=fK、L= K0.5L0.5,则 fλK、λL=λK0.5λL0.5 =λ0.5+0.5K0.5L0.5=λK0.5L0.5=λQ 故该生产过程是规模报酬不变;2资本K的投入量不变,而L为可变投入对于生产函数Q=K0.5L0.5,MPP L=0.5 K0.5L-0.5又 MPP L′= －0.25 K0.5L-1.5<0这表明：当资本使用量既定时,随着使用的劳动L的增加,劳动的边际产量是递减的;同样,MPP K=0.5 L0.5K-0.5 MPP K′= －0.25 L0.5K-1.5<0这表明：当劳动使用量既定时,随着使用的资本K的增加,资本的边际产量是递减的;下表是短期生产函数Q=fL、K的产量表：短期生产的产量表：1在表中填空2根据1画出TPL、、APL、、MPL曲线图;略3根据1,并假定劳动的价格w=200,完成下面相应的短期成本表;短期生产的成本表4根据3画出TVC、AVC和MC曲线;略6、假定某企业的短期成本函数TCQ=Q3—10Q2+17Q+66（1）指出该短期成本函数中的可变成本部分和不变成本部分;（2）写出下列相应的函数：TVCQ、ACQ、AVCQ、AFCQ、MCQ1TC=Q3－10Q2+17Q+66其中 VC= Q3－10Q2+17Q FC=662TVC= Q3－10Q2+17QAC= Q2－10Q+17 +66/QAVC= Q2－10Q+17AFC=66/QMC= 3Q2－20Q+177、已知某企业的短期成本函数STCQ=0.04Q3—0.8Q2+10Q+5,求最小的平均可变成本值;STC=0.04Q3－0.8Q2+10Q+5则TVC= 0.04Q3－0.8Q2+10QAVC= 0.04Q2－0.8Q+10AVC′=0即0.08Q－0.8=0Q=10这时AVC=6厂商理论1、假设完全竞争市场的需求函数和供给函数分别为Qd=50 000—2 000P和Qs=40 000+3 000P;求：（1）场均衡价格和均衡数量（2）商的需求函数1 Q d=50 000－2 000PQ s=40 000+3 000PQ d= Q s50 000－2 000P =40 000+3 000PP=2 Q=46 0002厂商的需求函数为 P=22、设某完全竞争厂商生产的某产品的边际成本函数为MC=0.4Q—12元/件,总收益函数为TR=20Q,且已知生产10件产品时总成本为100元,试求生产多少件时利润极大,其利润为多少已知MC=0.4Q－12 TR=20Q 则 P=MR=20利润最大时,MR=MC 即0.4Q－12 =20 Q=80时利润最大;又因MC= 0.4Q－12 , 则TC= 0.2Q2－12Q+FC又已知Q=10时,TC=100,即100=0.2×102－12 ×10+FC故 FC=200 因而总成本函数为TC= 0.2Q2－12Q+20Q=80时,p=TR－TC=PQ－0.2Q2－12Q+200=20×80－0.2 ×802－12 ×80 +200=10803、争厂商的短期成本函数为STC=0.04Q3—0.8Q2+10Q+5,求厂商的短期供给函数;AVC=0.04Q2－0.8Q+10MC= 0.12Q2－1.6Q+10令AVC=MC即 0.04Q2－0.8Q+10= 0.12Q2－1.6Q+10 解方程得,Q=10, Q=0舍去Q=10,当Q≥10时,MC≥AVC;于是厂商的短期供给函数为P=MC= 0.12Q2－1.6Q+10 Q ≥104、已知某完全竞争行业中单个厂商的短期成本函数为STC=0.1Q3—2Q2+15Q+10;试求：（1）当市场上产品的价格为P=55时,厂商的短期均衡产量和利润（2）当市场价格下降为多少时,厂商必须停产（3）厂商的短期供给函数1STC=0.1Q3－2Q2+15Q+10于是MC= 0.3Q2－4Q+15厂商的供给曲线为P=MC 当P=55时, 55= 0.3Q2－4Q+15则 0.3Q2－4Q－40=0 解方程得 Q=20,Q=﹣6.7舍去Q=20时,p=TR－TC=55×20－0.1×203－2×202+15×20+10=7902厂商停产时,P=AVC,而MC与AVC相交于AVC的最低点;TVC= 0.1Q3－2Q2+15QAVC= 0.1Q2－2Q+15AVC最低时, AVC′=0即0.2Q－2=0 Q=10 P=AVC=5即当市场价格下降为5时,厂商必须停产3厂商的短期供给函数为MC与AVC最低点相交之处以上的MC线;MC=TVC′ =0.3Q2－4Q +15所以厂商的短期供给函数：P= 0.3Q2－4Q +15 Q≥105、找出需求曲线P=12-3Q对应的边际收益曲线;MR=TR=12Q-3Q2=12-6Q6、某垄断厂商的产品的需求函数为P=12—0.4Q,总成本函数TC=0.6Q2+4Q+5;求：（1）Q为多少时总利润最大价格、总收益和总利润各为多少（2）（3）Q为多少时总收益最大价格、总收益和总利润各为多少（4）（5）Q为多少时总收益最大且π≥10价格、总收益和总利润各为多少（6）1利润最大的条件是MR=MC,已知P=12 － 0.4Q则MR=PQ′= 12 － 0.8Q又已知TC= 0.6Q2+4Q +5MC=1.2Q+4 MR=MC即12 － 0.8Q =1.2Q+4 则Q=4于是,P=12－0.4×4=10.4TR=41.6 p=TR －TC=112TR=PQ=12Q － 0.4Q2总收益最大,即TR′=012 － 0.8Q=0 于是 Q=15 又TR″=﹣ 0.8﹤0所以Q=15时TR最大;这时, P=6 TR=90 p=﹣1103既要使TR最大,又要使p≥10 p=TR －TC= 12Q － 0.4Q2 － 0.6Q2+4Q +5= －Q2 +8Q －5 ≥10 最少p=10即－Q2 +8Q －5=10 时得 Q1=3 Q2=5将Q1、 Q2分别代入TR=PQ中,得TR1=12－0.4 Q1Q1=32.4TR2=12－0.4 Q2Q2=50取其中TR大的值; 故当Q=5时,TR最大且p≥10 ;这时TR=50,p= 50 － 0.6×52+4×5+5=10P= 12 － 0.4Q =107、假设有两个寡头垄断厂商的行为遵循古诺模型,它们的成本函数分别为：TC1=0.1q12+20q1+100 000TC2=0.4q22+32q2+20 000这两个厂商生产一同质产品,其市场需求函数为： Q=4 000—10P 根据古诺模型,试求：1厂商1和厂商2的反应函数2均衡价格和厂商1和厂商2的均衡产量3厂商1和厂商2的利润1已知Q=4 000－10P则P=400 －0.1Q Q=q1+q2p1=TR1－TC1=400 q1－ 0.1 q12－ 0.1 q1 q2 － 0.1 q12－20 q1－100 000 p2=TR2－TC2=400 q2－ 0.1 q22－ 0.1 q1 q2 － 0.4q22－ 32 q2－20 000两厂商实现利润最大化的条件是：dp1/dq1=0dp2/dq2=0dp1/dq1=400－0.2 q1－0.1q2－0.2q1－200.4q1=380－0.1q2q1=950－0.25q2……厂商1的反应函数同样可求得：q2=368－0.1q1……厂商2的反应函数2均衡产量和均衡价格可从此二反应函数曲线的交点求得;q1=950 －0.25q2q2=368 －0.1q1联立解方程,得 q1=880 q2=280Q=q1+q2 =1160P=400 －0.1×1160=2843 p1=Pq1－TC1=284 ×880－0.1 ×880 2+20 ×880 +100 000=54 880 p2=Pq2－TC2 =284 ×280－0.4×280 2+32 ×280+20 000=19 200要素价格理论1、假定某特定劳动力市场的供求曲线分别为：DL=6 000-100W,SL=100W;试求：1均衡工资为多少2如政府对工人提供的每单位劳动课以10美元的税,则新的均衡工资为多少3实际上对单位劳动征收的10美元税收由谁支付4政府征收的总税收额是多少1市场均衡时,S L=D L即 6 000－100W=100W W=30美元2政府征税10美元后,S L′=100W′－10 S L′=D L即100W′－10 =6 000－100W′ W′=35美元3征税后厂商购买的劳动价格为35$,征税前为30$,故其中5$为厂商支付的税额;征税政策实施后工人提供每单位劳动获得35$,纳税后剩25$,比征税前的30$少了5$,此为工人实际支付的税款;这里,厂商、工人平均承担了政府征收的10税款;4征税后,W=35美元,这时厂商的劳动需求量L=25000,因此,政府征收的税收额T=10·L=10·25000=25万美元;2、假定对劳动的市场需求曲线为DL= ―10W+150,劳动的供给曲线SL=20W,其中DL、、SL分别为劳动市场需求、供给的人数,W为每日工资;1求该市场中劳动与工资的均衡水平;2如果政府想要把工资提高到6元/日,其方法是将钱直接补贴给企业,然后由企业给工人提高工资;这时政府需补贴给企业多少新的就业水平是多少3如果政府不直接补贴给企业,而是宣布法定最低工资为6元/日,则在这个工资水平下将需求多少劳动失业人数是多少1市场均衡时,S L=D L即﹣10W+150=20W W=5元这时 Q L= S L=D L=100人2当均衡工资提高到W′=6元时, QL ′= DL′= SL′=6×20=120即新的就业水平为120人;假设政府给予企业补贴X元,则补贴后劳动需求：D L′=10W′－X+150,其中, W′=6, Q L′=S L′=120, X=3政府给予企业补贴额=3×120=360企业付给职工的补贴为W′－WQ L′=6－5120=1203法定最低工资为6元/日时,D L=﹣10×6+150=90人S L=20×6=120人故失业人数为： S L－D L=30人3、某厂商只把劳动作为可变要素,其生产函授数为Q= -0.01L3+L2+36L,Q为厂商每天产量,L为工人的日劳动小时数;所有市场均为完全竞争的,单位产品价格为0.1美元,小时工资率为4.8美元,试求当厂商利润最大时：（1）商每天将投入多少劳动小时（2）如果厂商每天支付的固定成本为50美元,厂商每天所得的利润是多少1Q= -0.01L3+L2+36LP=0.1 W=4.8当厂商利润极大时W=VMP L=P·MPP L即 4.8=0.1×-0.03L2+2L+360.03L2－2L+12=0 L1=60L2=20/3舍去,因为L=20/3时,dMPP L/dL=-0.06L+2=1.6﹥0所以,L=60,即厂商每天投入劳动60小时;2p=TR-TC=P·Q-FC+VC= P·Q-50+W·L=22市场失灵与政府干预1、垄断是如何造成市场失灵的2、外部性的存在是如何干扰市场对资源的配置的3、公共物品为什么不能靠市场来提供4、市场机制能够解决信息不完全和信息不对称问题吗。

第四章1。

（1)利用短期生产的总产量（TP ）、平均产量(AP ）和边际产量（MP ）之间的关系，可以完成对该表的填空，其结果如下表:(2）所谓边际报酬递减是指短期生产中一种可变要素的边际产量在达到最高点以后开始逐步下降的这样一种普遍的生产现象。

本题的生产函数表现出边际报酬递减的现象，具体地说，由表可见，当可变要素的投入量由第4单位增加到第5单位时,该要素的边际产量由原来的24下降为12。

2．（1）.过TPL 曲线任何一点的切线的斜率就是相应的MPL 的值。

（2）连接TPL 曲线上热和一点和坐标原点的线段的斜率，就是相应的APL 的值。

（3)当MPL >APL 时，APL 曲线是上升的。

当MPL <APL 时，APL 曲线是下降的。

当MPL=APL时,APL曲线达到极大值。

3.解答：（1)由生产数Q=2KL-0。

5L2-0。

5K2，且K=10,可得短期生产函数为:Q=20L-0.5L2—0。

5*102=20L—0.5L2-50于是,根据总产量、平均产量和边际产量的定义，有以下函数：劳动的总产量函数TP L=20L—0.5L2-50劳动的平均产量函数AP L=20-0。

5L—50/L劳动的边际产量函数MP L=20-L(2）关于总产量的最大值：20—L=0解得L=20所以，劳动投入量为20时，总产量达到极大值。

关于平均产量的最大值:-0.5+50L—2=0L=10（负值舍去）所以，劳动投入量为10时,平均产量达到极大值。

关于边际产量的最大值：由劳动的边际产量函数MP L=20—L可知，边际产量曲线是一条斜率为负的直线。

考虑到劳动投入量总是非负的，所以，L=0时，劳动的边际产量达到极大值。

(3)当劳动的平均产量达到最大值时，一定有APL=MPL。

由（2）可知，当劳动为10时，劳动的平均产量APL达最大值，及相应的最大值为：APL的最大值=10MPL=20-10=10很显然APL=MPL=104。

第四章生产函数第一部分教材配套习题本习题详解一、简答题1. 如何准确区分生产的短期和长期这两个基本概念?生产的短期：指生产者来不及调整全部生产要素的数量，至少有一种生产要素的数量是固定不变的时间周期。

短期不可调整的生产要素称不变生产要素，一般包括厂房、大型设备、高级管理者、长期贷款等，可调整的生产要素成为可变生产要素，一般包括原材料、燃料、辅助材料、普通劳动者等。

生产的长期：指生产者可以调整全部生产要素的数量的时间周期。

生产的短期和长期是相对的时间概念,不是绝对的时间概念，其与企业所属行业、所用技术设备和规模等因素有关。

2.下面是一张一种可变生产要素的短期生产函数的产量表（表４—１）：（１）在表中填空。

（２）该生产函数是否表现出边际报酬递减？如果是，是从第几单位的可变要素投入量开始的？—解答：（１）在表４—１中填空得到表４—２。

3．区分边际报酬递增、不变和递减的情况与规模报酬递增、不变和递减的情况。

解答：边际报酬变化是指在生产过程中一种可变要素投入量每增加一个单位时所引起的总产量的变化量，即边际产量的变化，而其他生产要素均为固定生产要素，固定要素的投入数量是保持不变的。

边际报酬变化一般包括边际报酬递增、不变和递减三个阶段。

很显然，边际报酬分析可视为短期生产分析。

规模报酬分析方法是描述在生产过程中全部生产要素的投入数量均同比例变化时所引起的产量变化特征，当产量的变化比例分别大于、等于、小于全部生产要素投入量变化比例时，则分别为规模报酬递增、不变、递减。

很显然，规模报酬分析可视为长期生产的分析视角。

区别：①前提条件不同，边际报酬变化生产要素分为不变和可变生产要素，生产要素比例发生变化；规模报酬分析研究生产要素同比例变动。

②考察时间长短不同。

边际报酬变化分析的是短期生产规律；规模报酬研究长期生产规律。

③指导意义不同。

边际报酬变化指出要按比例配置生产要素；规模报酬指出要保持企业的适度规模。

④由于前提条件不同，两规律独立发挥作用，不存在互为前提，互为影响关系。

《经济学基础（第6版）》思考题解答第1章1.如何理解资源是稀缺的？一般的，相对于人类社会的无限欲望而言，生产人类所需物品的资源总是不足的，这就是资源的稀缺性。

资源的稀缺性不是指资源绝对数量的多少，而是指相对于无限的欲望而言，再多的资源也是不足的。

即稀缺性是就相对意义而言的。

欲望的基本特点在于无限性，即人们的欲望永远没有完全得到满足的时候。

人的欲望要用各种物品或劳务来满足，而物品要用各种资源来生产，这些资源包括人力资源和自然资源。

然而，人类赖以生存的地球的资源是有限的，这样无限的欲望和有限的资源的矛盾就形成了经济学所说的稀缺性。

2.说明人类社会所面临的基本经济问题。

面对资源稀缺性的事实，人类社会都必须面对和解决三个基本的经济问题。

他们是：生产什么；如何生产；为谁生产。

（1）生产什么商品和生产多少。

一个社会必须决定，在诸多可能的物品和劳务中每一种应该生产多少以及何时生产。

（2）如何生产物品。

一个社会必须决定谁类生产，使用何种资源，以及采用何种生产技术。

（3）为谁生产。

一个社会必须决定谁来享用经济活动的成果；社会产品如何在不同的居民之间进行分配；收入和财富的分配是否公平合理；是否会出现贫富差距。

3.微观经济学和宏观经济学有什么不同和联系？微观经济学以单个经济单位为研究对象，通过研究单个经济单位的经济行为和相应经济变量数值的决定来说明价格机制如何解决社会的资源配置问题。

可见，微观经济学研究的对象是单个经济单位的经济行为，即家庭和企业的经济行为。

微观经济学解决的问题是资源配置。

微观经济学的中心理论是价格理论。

微观经济学的研究方法是个量分析。

相对而言，宏观经济学以整个国民经济为研究对象，通过研究经济中各有关总量的决定以及变化来说明资源如何才能得到充分利用。

可见，与微观经济学的几个方面相对应的，宏观经济学研究的对象是整个经济，而不是经济中的各个单位。

宏观经济学解决的问题是资源利用。

它把资源配置作为既定前提，研究现有资源未能得到充分利用的原因，达到充分利用的途径以及如何增长等问题。

第四章练习题参考答案1.（1）利用短期生产的总产量（TP）、平均产量（AP）和边际产量（MP）之间的关系，可以完成对该表的填空，其结果如下表：可变要素的数量可变要素的总产量可变要素平均产量可变要素的边际产量1 2 2 22 12 6 103 24 8 124 48 12 245 60 12 126 66 11 67 70 10 48 70 35/4 09 63 7 -7（2）所谓边际报酬递减是指短期生产中一种可变要素的边际产量在达到最高点以后开始逐步下降的这样一种普遍的生产现象。

本题的生产函数表现出边际报酬递减的现象，具体地说，由表可见，当可变要素的投入量由第4单位增加到第5单位时，该要素的边际产量由原来的24下降为12。

2．（1）.过TPL曲线任何一点的切线的斜率就是相应的MPL的值。

（2）连接TPL曲线上热和一点和坐标原点的线段的斜率，就是相应的APL的值。

（3）当MPL>APL时，APL曲线是上升的。

当MPL<APL时，APL曲线是下降的。

当MPL=APL时，APL曲线达到极大值。

3.解答：（1）由生产数Q=2KL-0.5L2-0.5K2,且K=10，可得短期生产函数为：Q=20L-0.5L2-0.5*102=20L-0.5L2-50于是，根据总产量、平均产量和边际产量的定义，有以下函数：劳动的总产量函数TPL=20L-0.5L2-50劳动的平均产量函数APL=20-0.5L-50/L劳动的边际产量函数MPL=20-L（2）关于总产量的最大值：20-L=0解得L=20所以，劳动投入量为20时，总产量达到极大值。

关于平均产量的最大值：-0.5+50L-2=0 L=10（负值舍去）所以，劳动投入量为10时，平均产量达到极大值。

关于边际产量的最大值：由劳动的边际产量函数MPL=20-L可知，边际产量曲线是一条斜率为负的直线。

考虑到劳动投入量总是非负的，所以，L=0时，劳动的边际产量达到极大值。

一、单项选择题(只有一个选项正确，共14道小题)1. 在维持产量水平不变的条件下，如果企业增加2单位的劳动投入量就可以减少4单位的资本投入量，则有（）(A)(B)(C)(D)你选择的答案：未选择 [错误]正确答案：C解答参考：2. 在以横轴表示劳动数量和纵轴表示资本数量的平面坐标中所绘出的等成本线的斜率为（）(A)(B)(C)(D)你选择的答案：未选择 [错误]正确答案：B解答参考：3. 对于生产函数和成本方程而言,在最优的生产要素组合点上应该有( )(A)(B) 等产量曲线和等成本线相切(C)(D) 上述说法都对你选择的答案：未选择 [错误]正确答案：D解答参考：4. 等成本线平行向内移动,则( )(A) 产量减少(B) 成本增加(C) 生产要素价格按相同比例提高(D) 生产要素价格按相同比例降低你选择的答案：未选择 [错误]正确答案：C解答参考：5. 下列各项中，正确的是（）(A) 只要边际产量减少，平均产量就减少(B) 只要总产量减少，边际产量就一定为负值(C) 只要边际产量减少，总产量就减少(D) 只要平均产量减少，总产量就减少你选择的答案：未选择 [错误]正确答案：B解答参考：6. 理性的厂商将让生产过程在( )进行(A) 第一阶段(B) 第二阶段(C) 第三阶段(D) 不能确定你选择的答案：未选择 [错误]正确答案：B解答参考：7. 当厂商以最小成本生产出既定产量时，则其（）(A) 一定获得最大利润(B) 总收益为零(C) 未获得最大利润(D) 不能确定获得最大利润正确答案：A解答参考：8. 对应于边际报酬的递增阶段,STC曲线( )(A) 以递增的速率上升(B) 以递减的速率上升(C) 以递增的速率下降(D) 以递减的速率下降正确答案：B解答参考：9. 机会成本的经济含义是( )(A) 使用一种资源的机会成本是放弃这种资源另一种用途的收入(B) 使用一种资源的机会成本是放弃这种资源在其他用途中所能得到的最高收入(C) 使用一种资源的机会成本是放弃这种资源用于次优用途的收入(D) 使用一种资源的机会成本是放弃这种资源继续使用而必须支付的费用正确答案：B解答参考：10. 在任何产量上的LTC决不会大于该产量上由最优生产规模所决定的STC。

第四章生产函数第一部分教材配套习题本习题详解一、简答题1. 如何准确区分生产的短期和长期这两个基本概念?生产的短期：指生产者来不及调整全部生产要素的数量，至少有一种生产要素的数量是固定不变的时间周期。

短期不可调整的生产要素称不变生产要素，一般包括厂房、大型设备、高级管理者、长期贷款等，可调整的生产要素成为可变生产要素，一般包括原材料、燃料、辅助材料、普通劳动者等。

生产的长期：指生产者可以调整全部生产要素的数量的时间周期。

生产的短期和长期是相对的时间概念,不是绝对的时间概念，其与企业所属行业、所用技术设备和规模等因素有关。

2.下面是一张一种可变生产要素的短期生产函数的产量表（表４—１）：（１）在表中填空。

（２）该生产函数是否表现出边际报酬递减？如果是，是从第几单位的可变要素投入量开始的？—解答：（１）在表４—１中填空得到表４—２。

3．区分边际报酬递增、不变和递减的情况与规模报酬递增、不变和递减的情况。

解答：边际报酬变化是指在生产过程中一种可变要素投入量每增加一个单位时所引起的总产量的变化量，即边际产量的变化，而其他生产要素均为固定生产要素，固定要素的投入数量是保持不变的。

边际报酬变化一般包括边际报酬递增、不变和递减三个阶段。

很显然，边际报酬分析可视为短期生产分析。

规模报酬分析方法是描述在生产过程中全部生产要素的投入数量均同比例变化时所引起的产量变化特征，当产量的变化比例分别大于、等于、小于全部生产要素投入量变化比例时，则分别为规模报酬递增、不变、递减。

很显然，规模报酬分析可视为长期生产的分析视角。

区别：①前提条件不同，边际报酬变化生产要素分为不变和可变生产要素，生产要素比例发生变化；规模报酬分析研究生产要素同比例变动。

②考察时间长短不同。

边际报酬变化分析的是短期生产规律；规模报酬研究长期生产规律。

③指导意义不同。

边际报酬变化指出要按比例配置生产要素；规模报酬指出要保持企业的适度规模。

④由于前提条件不同，两规律独立发挥作用，不存在互为前提，互为影响关系。