--非正弦交流电路
- 格式:doc
- 大小:1.96 MB
- 文档页数:21

习题课一:非正弦式交流电有效值的计算与应用一、交流电有效值的定义:指对做功或发热有效。
让某个交流电和一个直流电对同样大小的电阻加热,如果在相等的时间内它们产生的热量相等,那么交流电的有效值就等于直流电的数量大小。
(注意4个相等:被加热电阻相等、时间相等、发热量相等,则交流电的有效值与直流的数量大小相等)交流电的有效值是根据电流的热效应来规定的,与电流的方向无关,但一般与所取的时间的长短有关,在无特别说明时,是以一个周期的时间来计算有效值的。
二、3个结论提示:⑴、按此定义某一直流电的有效值就是直流电本身。
应用见例1。
⑵、线性变化电流的有效值=平均值=(最大值+最小值)÷2。
⑶、“完整”的标准正弦交流电的有效值和最大值的关系为:E E m 2=,I I m 2=,U U m 2=。
注意:如果通电时间较短(短至1/4周期),但在起止时刻恰好等于正余弦的0值或峰值,也是满足前述关系的,见例2。
如果起止时刻不等于正余弦的0值或峰值,就不成立,见例0。
例0:有一正弦交流电的最大值为10伏,加在一直流电阻为10欧的纯电阻上。
已知它的周期为0.2秒,则它在0.05秒内的发热量可能为:(A 、B 、C )A 大于0.25焦,B 小于0.25焦,C 等于0.25焦,D 一定为0.25焦。
三、非正弦式交流电有效值的计算方法与例题方法说明:⑴、按有效值的定义通过加热来计算。
⑵、通常计算工作一个周期内的发热量。
⑶、为计算为一个周期内的发热量,焦耳热公式中所用的U 和I 仍然需要是有效值,如例3中前2秒内的有效值是20/2,后1秒内的有效值是10/2。
具体步骤:1、分析一个周期内不同时间段的电流特点,确认每一时段的有效值。
2、计算它在一个周期内的发热量。
3、根据有效值定义(交流、直流发热量相等)列方程计算出有效值。
【例1】计算下图所示交流电的有效值,如果该交流电加在一个5Ω的电阻元件上,它在4个周期内产生的焦耳热是多少。








电路名词解释1 电流(current):电荷在电场力作用下的有序运动形成电流,衡量电流大小的量是电流强度,简称电流。
其量值为单位时间内通过电路某一导体横截面的电荷量。
用符号i(t)表示,单位为A(安培)。
2 电压(voltage):电场力将单位正电荷由一点移到另一点时所做的功,是衡量电场力做功能力的物理量。
用符号u(t )表示,单位为V (伏特)。
3 电动势(electromotive force):电源中的局外力(非电场力)将单位正电荷从电源负极移到电源正极所做的功,是衡量局外力做功能力的物理量。
用符号e(t )表示,单位为V(伏特)。
4 电位(electric potential):在电路中任选一点为参考点,由某点到参考点之间的电压称为该点的电位,用符号V表示,单位为V(伏特)。
5 电能(electrical energy):在一段时间内电场力所做的功称为电能,用符号W表示,单位为J(焦耳)。
6 戴维宁定理(Thevenin’s theorem):在线性电路中,任何一个含有独立源的二端网络,对外电路而言,可以用一个理想电压源与电阻串联的电路等效代替。
电压源的电压等于有源二端网络的开路电压,电阻等于有源二端网络中所有独立电源置零后的等效电阻。
7 叠加定理(superposition theorem):在线性电路中,任一支路的电流或电压,均等于电路中各个独立电源单独作用时,在该支路产生的电流或电压的代数和。
8 基尔霍夫电流定律(Kirchhoff’s current law简称KCL):电路中任一瞬间,流入任一结点的支路电流之和恒等于流出该结点的支路电流之和。
或表述为电路中任一瞬间,任一结点的支路电流的代数和恒等于零。
9 基尔霍夫电压定律(Kirchhoff’s voltage law简称KVL):电路中任一瞬间,任一回路各元件电压升之和恒等于电压降之和。
或表述为电路中任一瞬间,任一回路各支路电压的代数和恒等于零。

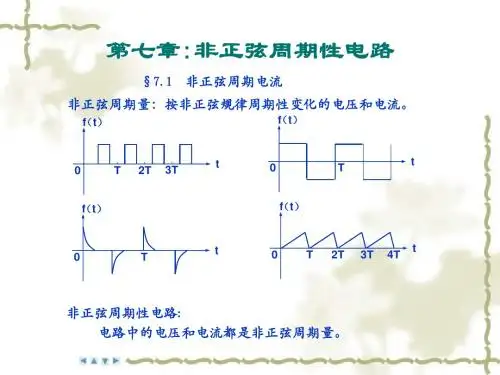
第7章 非正弦周期交流电路7.1非正弦周期交流电路习题一、填空题1.非正弦周期信号可以分解成________________________________________________,用数学中的——————————————————级数表示。
2.非正弦周期信号的谐波成分可能有直流分量(零次谐波)、奇次谐波及——————谐波。
3.电话中使用的电信号是——————(填正弦或非正弦)周期信号。
4.非正弦周期信号频谱的含义是——————————————————————————。
5.非正弦周期信号的频谱有————————————————————————————等特点。
6.频谱知识在——————————————————————领域中要用到频谱可以用仪器来测量,该仪器的名称叫———————————————————————。
7.请画出半波整流波形的频谱————————————————————————————。
8、非正弦周期交流电的有效值与它的各次谐波有效值之间的关系是——————————。
9、非正弦周期交流电的平均值指的是——————————(填写数学平均值还是绝对平均值)。
10、非正弦周期交流电的有效值和平均值————————(填写是或不)相同的。
11、非正弦周期交流电的最大值指的是——————————————,最大值与有效值之间——————(填写有或者没有)√2 倍关系。
12、线性非正弦周期电路的分析计算方法叫————————,它的依据是————————。
13.用谐波分析法求出电路中的各次谐波的电流分量后,应将电流分量的——————值(填写瞬时、有效或者相量)进行叠加求电路的非正弦电流。
14.若三次谐波的3L X =9Ω、3C X =6Ω,则一次谐波的1L X ——————,1C X ——————。
15.非正弦周期交流电的平均功率的公式是————————,同次谐波的电流、电压之间——————(填写:能或不能)产生平均功率。
第9章非正弦交流电路学习指导与题解一、基本要求1.建立几个频率为整数倍的正弦波可以合成为一非正弦周期的概念。
明确一个非正弦周期波可以分解为一系列频率为整数倍正弦波之和的概念(即谐波分析)、谐波中的基波与高次谐波的含义。
了解谐波分析中傅里叶级数的应用。
2.掌握波形对称性与所含谐波分量的关系。
能根据波形的特点判断所含谐波的情况。
了解波形原点选择对所含谐波的影响。
3.掌握非正弦周期电压和电流的平均值(即直流分量)和有效值的计算。
能根据给定波形计算出直流分量。
能根据非正弦周期波的直流分量和各次谐波分量,计算出它的有效值。
4.掌握运用叠加定理和谐波分析计算非正弦交流电路中的电压和电流的方法。
5.建立同频率的正弦电压和电流才能形成平均功率的概念。
掌握运用叠加定理和谐波分量计算非正弦交流电路中和平均功率。
二、学习指导在电工技术中,电路除了激励和响应是直流和正弦交流电和情况外,也还遇到有非正弦周期函数电量的情况。
如当电路中有几个不同频率的正弦量激励时,响应是非正弦周期函数;含有非线性元件的电路中,正弦激励下的响应也是非线性的;在电子、计算机等电路中应用的脉冲信号波形,都是非正弦周期函数。
因此,研究非正弦交流电路的分析,具有重要和理论和实际意义。
本章的教学内容可分为如下三部分:1.非正弦周期波由谐波合成的概念;2.非正弦周期波的谐波分析;3.非正弦交流电路的计算。
着重讨论非正弦周期波谐波分析的概念,非正弦周期量的有效值和运用叠加定理计算非正弦交流电路的方法。
现就教学内容中的几个问题分述如下。
(一)关于非正弦周期波的谐波的概念非正弦周期波是随时间作周期性变化的非正弦函数。
如周期性变化的方波、三角波等。
这类波形,与正弦波相比,都有变化的周期T和频率f,不同的是波形而已。
f t,可几个频率为整数倍的正弦波,合成是一个非正弦波。
反之,一个非正弦周期波()以分解为含直流分量(或不含直流分量)和一系列频率为整数倍的正弦波。
这些一系列频率为整数倍的正弦波,就称为非正弦周期波的谐波。
其中频率与非正弦周期波相同的正弦波,称为基波或一次谐波;频率是基波频率2倍的正弦,就称为二次谐波;频率是基波频率3倍的正弦波,称为三次谐波;频率是基波频率k 倍的正弦波,称为k 次谐波,k 为正整数。
人们通常将二次及二次以上的谐波,统称为高次谐波。
(二)关于谐波分析的方法在电路分析中,将非正弦周期波的分解,应用傅里叶级数展开的方法,分解为直流分量(或不含有)和频率为整数倍的一系列正弦波之和,称为傅里叶分析,又称为谐波分析。
一人周期为T 的函数()f t ,如果满足狄里赫利条件﹡,则()f t 可以展开为如下三角级数:01()(cos sin )k k k f t A A k t B k t ωω∞==++∑这是一个无穷级数,由法国人傅里叶(Fourier )提出来的,故称为傅里叶级数。
式中0A ,k A ,k B 称为傅里叶系数,由如下公式计算得出:00001()()2()cos 2()sin TTk Tk A f t dtT A f t k tdtT B f t k tdtT ωω===⎰⎰⎰直流分量0A 是()f t 一周期时间内的平均值,称直流分量。
1k =的正弦波,称为基波;2k =的正弦波,称为二次谐波;k n =的正弦波,称为n 次谐波。
当k 为奇数时,称为奇次谐波;k 为偶数时,称为偶次谐波。
非正弦周期波的傅里叶级数展开,关键是计算傅里叶系数的问题。
在电工技术中,遇到的非正弦周期波,都满足狄里赫利条件的,均可展开为傅里叶级数。
常见的非正弦周期波的傅里叶级数展开式,已在手册及教材中列出,如下表所示,以供查用。
常见非正弦周期波的傅里叶级数展开式()f t 波 形 图()f x 傅里叶级数展开式22()(1sin cos 2cos 4)2315mA f t t t t πωωωπ=+---L﹡ 狄利赫利条件:()f t 在〔2T -,2T 〕 或〔0,T 〕区间,(1)除有限个第一类间断点外,其余各点连续;(2)只有有限个极点。
()f t 波 形 图()f x 傅里叶级数展开式2222()(1cos 2cos 4cos6)31535m f t A t t t ωωωπ=----L411()(sin sin 3sin 5)35m f t A t t t ωωωπ=+++L211()(sin sin 2sin 3)23m f t A t t t ωωωπ=-+-L1111()[(sin sin 2sin 3)]223m f t A t t t ωωωπ=-+++L2811()(sin sin 3sin 5)925m f t A t t t ωωωπ=-+-L2811()(cos cos3cos5)925m f t A t t t ωωωπ=+++L411()(sin sin sin 3sin 3sin 5sin 5)925m f t A t t t αωαωαωαπ=+++L331111()(cos3cos 6cos9)283580m f t A t t t ωωωπ=+-+-L(三)关于波形对称性与所含谐波分量的关系在电工技术中遇到的非正弦周期波,许多具有某种对称性。
在对称波形中,傅里叶级数中,有些谐波分量(包括直流分量。
因直流分量是0k =的零次谐波分量)不存在。
因此,利用波形对称性与谐波分量的关系,可以简化傅里叶系数的计算。
1.波形对称性与谐波分量的关系 有如下几个对称性与谐波分量的关系 有如下几个对称性波形及其傅里叶系数情况。
(1)偶函数 ()f t 波形对称于纵坐标,满足()f t =()f t -条件,如图9-1所示。
则0k B =,傅里叶级数中只含0A 和cos k A k t ω∑项,k =1,2,3,…。
亦即这类对称性非正弦周期波,只含直流分量和一系列余弦 函数的谐波分量。
(2)奇函数 ()f t 波形对称于坐标原点,满足 图9-1 偶函数波形举例()()f t f t =--条件,如图9-2所示。
则00A =,k A=0,傅里叶级数中,只含sin kB k t ω∑项,k =1,2,3,…。
亦即这类对称性非正弦周期波,只含一系列正弦函数的谐波分量。
(3)奇半波对称函数 若()f t 波形移动半周()2T ±与 原波形成镜像,即对横轴对称,满足()()2Tf t f t =-±条件。
如图9-3所示,()f t 波形不对称于纵轴和原点,故它图9-2 奇函数举例 不是偶函数和奇函数,只是移动()2T±与原波形对称于 横轴,则傅里叶系数中,00A =,k A 和k B 中k 为奇数,即k =1,3,5,…。
这类非正弦周期波只含奇次谐波。
所以,这类奇半波对称函数()f t ,称为奇谐波函数。
以上是三种对称波形及其谐波分量情况,下面 再介绍半波重叠波和四种双重对称性波形及其谐波 分量情况。
(4)半波重叠函数 若()f t 波形移动半波()2T ± 与原波形重叠,满足()()2Tf t f t =±条件。
如图9-4 所示,()f t 不对称于纵轴和原点,故它不是偶函数和 奇函数,只是移动2T±与原波形重叠。
则傅里叶系数 图 9-3 奇半波对称波形举例k A 和k B 中k 为偶数,即k =0,2,4,6,…。
这类非正弦周期波只含偶次谐波。
所以,这类半波重叠函数,称为偶偕波函数。
图 9-4 半波重叠函数波形举例 图 9-5 奇函数且半波对称波形举例(5)奇函数且奇半波对称 若()f t 波形满足()()f t f t =--和()()2Tf t f t =-±两个条件。
如图9-5所示,()f t 波形对称于原点,是奇函数,且移动2T±与原波形对横轴成镜像对称,又是奇半波对称函数。
则傅里叶系数中00A =,0k A =,k B 中k 为奇数,即k =1,3,5…。
傅里叶级数中只含sin kB k t ω∑项的奇次谐波。
所以,这类奇函数且半波对称波,只含正弦函数的奇次谐波。
(6) 偶函数且奇半波对称 ()f t 波形满足()f t=()f t -和()()2Tf t f t =-±两个条件。
如图9-6所示,()f t 波形对称于纵坐标,是偶函数,且移动2T±与原波形对横轴成镜像对称,又是奇半波对称函数。
则傅里叶系000k A B ==,k A 中k 为奇数,即k =1,3,5…。
傅里叶级数中只含cos kA k t ω∑项的奇次谐波。
所以,这类偶函数且奇半波对称对称波,只含余弦函数的奇次谐波。
(7)偶函数且半波重叠 ()f t 波形满足()()f t f t =-和()()2Tf t f t =±两个条件。
如图9-7所示,()f t 波形对称于纵轴,是偶函数,且移动2T±与原波形重叠,又是半波重叠函数。
则傅里叶系数中,0k B =,k A 中k 为偶函数,即k =0,2,4,6,…。
傅里叶级数中只含0A 和cos kA k t ω∑项的偶次谐波。
所以,这类偶函数且半波重叠波,只含余弦函数的偶次谐波,包含直流分量。
(8)奇函数且半波重叠 ()f t 波形满足()()f t f t =--和()()2Tf t f t =±两个条件,如图9-8所示。
()f t 波形对称于原点,是奇函数,且移动2T±与原波形重叠,又是半波重叠函数。
则傅里叶系数中,00A =,0k A =,k B 中的k 为偶数,即k =2,4,6,…。
傅里叶级数中只含sin kB k t ω∑项的偶次谐波。
所以,这类奇函数且半波重叠波,只含正弦函数的偶次谐波。
图9-7 偶函数且半波重叠波形举例 图 9-8 奇函数且半波重叠波形举例﹡2。
非对称性非正弦周期波谐波分析的简化计算(1)非对称性非正弦周期波()f t ,可以分解为偶部()ef t 和奇部0()f t 之和。
偶部()ef t 是对称于纵轴的偶函数,奇部0()f t 是对称于原点的奇函数。
即 0()()()ef t f t f t =+1()[()()]2e f t f t f t =+-01()[()()]2f t f t f t =--图9-9 非对称性非正弦周期波()u t 及其偶部()eut 和奇部0()u t 波形图然后,利用波形的对称性来简化傅里叶系数的计算。
例如,如图9-9(a )所示的非对称性非正弦周期电压波()u t ,它的偶部()eu t 为如图9-9(b )所示,是偶函数且半波重叠波,从上述波形对称性可知,它的傅里叶级数只含0A 和cos kA k t ω∑项的偶次谐波。
即2111()[cos 2cos 4cos6]31535e mmU U u t t t t ωωωππ=+----L 奇部0()u t 如图9-9(c )所示,它是一正弦函数,即01()sin 2m u t U t ω=故非对称性非正弦周期波()u t 的傅里叶级数展开式为0()()()21sin [cos 22311cos 4cos 6]1535e m m m u t u t u t U U U t t t t ωωππωω=+=++----L(2)将非对称性非正弦周期波移动坐标原点位置,便可提到对称性波形,从而可以简化傅里叶级数展开式的计算。