第四章 正弦交流电路习题参考答案

电工基础习题册参考答案在学习电工基础的过程中，做习题是巩固知识、提升技能的重要环节。

这本习题册涵盖了众多关键知识点，以下是详细的参考答案。

首先，让我们来看第一章“电路的基本概念和基本定律”的习题。

对于概念性的题目，比如“什么是电路？电路的组成部分有哪些？”答案是：电路是电流通过的路径，它由电源、负载、导线和开关等组成。

电源提供电能，负载消耗电能，导线连接电路元件，开关控制电路的通断。

再看计算类的题目，例如“已知电路中某段电阻为 5 欧姆，通过的电流为 2 安培，求这段电阻两端的电压。

” 根据欧姆定律 U ＝ IR，可得出电压 U ＝ 2×5 ＝ 10 伏特。

第二章“电路的分析方法”中，有关于支路电流法、节点电压法和回路电流法的习题。

以一道用支路电流法求解的题目为例：“在一个具有三条支路的电路中，已知两条支路的电阻分别为 10 欧姆和 20 欧姆，电源电压为 30伏特，求各支路的电流。

” 我们设三条支路的电流分别为 I1、I2、I3，根据基尔霍夫定律列出方程组：I1 ＋ I2 ＋ I3 ＝ 0 （节点电流定律），10I1 ＋ 20I2 ＝ 30 （回路电压定律），解这个方程组可得 I1 ＝ 2 安培，I2 ＝ 1 安培，I3 ＝－3 安培（负号表示电流方向与假设方向相反）。

节点电压法的题目，如“在一个具有四个节点的电路中，已知三个节点的电位分别为 5 伏特、10 伏特和 15 伏特，各支路电阻分别为 1 欧姆、2 欧姆和 3 欧姆，求第四个节点的电位。

” 我们先设第四个节点的电位为 V4，然后根据节点电压法的公式列出方程，经过计算可得出V4 的值。

第三章“电路的暂态分析”，涉及到电容、电感的暂态过程。

像“一个电容初始电压为 0 伏特，充电至 10 伏特，电容值为 10 微法，求充电时间常数。

” 答案是：充电时间常数τ ＝ RC ＝ 10×10×10^（－6) ＝ 1×10^（－4) 秒。

工学第六版课后答案第一章习题1－1 指出图1－1所示电路中A 、B 、C 三点的电位。

图1－1 题 1－1 的电路解：图（a ）中，电流 mA I 51226.=+=, 各点电位 V C = 0 V B = 2×1.5 = 3V V A = (2+2)×1.5 = 6V图（b ）中，电流mA I 1246=+=， 各点电位 V B = 0 V A = 4×1 = 4VV C =－ 2×1 = －2V图（c ）中，因S 断开，电流I = 0， 各点电位 V A = 6V V B = 6VV C = 0图（d ）中，电流mA I 24212=+=， 各点电位 V A = 2×(4+2) =12V V B = 2×2 = 4V V C = 0图（e ）的电路按一般电路画法如图，电流mA I 12466=++=， 各点电位 V A = E 1 = 6VV B = (－1×4)+6 = 2V V C = －6V1－2 图1－2所示电路元件P 产生功率为10W ，则电流I 应为多少? 解：由图1－2可知电压U 和电流I 参考方向不一致，P = －10W ＝UI 因为U ＝10V , 所以电流I ＝－1A图 1－2 题 1－2 的电路1－3 额定值为1W 、10Ω的电阻器，使用时通过电流的限额是多少？ 解：根据功率P = I 2 R A R P I 3160101.===1－4 在图1－3所示三个电路中，已知电珠EL 的额定值都是6V 、50mA ，试问哪个电珠能正常发光？图 1－3 题 1－4 的电路解：图（a ）电路，恒压源输出的12V 电压加在电珠EL 两端，其值超过电珠额定值，不能正常发光。

图（b ）电路电珠的电阻Ω=Ω==120120506K R .，其值与120Ω电阻相同，因此电珠EL 的电压为6V ，可以正常工作。

图（c ）电路，电珠与120Ω电阻并联后，电阻为60Ω，再与120Ω电阻串联，电珠两端的电压为V 4126012060＝＋⨯小于额定值，电珠不能正常发光。

·第4章习题参考答案4.1 已知正弦交流电压220 V U =，f=50 Hz ，u =30ψ︒。

写出它的瞬时值式，并画出波形。

解： 0()2202sin(31430)V u t t =+4.2 已知正弦交流电流m =10 V I ，f=50 Hz ，i =45ψ︒。

写出它的瞬时值式，并画出波形。

解： ()︒+=45314sin 10t i4.3 比较以下正弦量的相位 （1）1u =310sin t+90ω︒（）V ，2u =537sin t+45ω︒（）V（2）u=1002sint+30ω︒（）V ，i=10cos t ωA （3）u=310sin100t+90︒（）V ，i=10sin1000t A （4）1i =100sin 314t+90︒（）A，2i =50sin 100t+135 π︒A （）解：（1）︒=︒-︒=454590ϕ，电压1u 超前电压2u ︒45（2）()10sin 90i t ω=+︒，︒=︒-︒=60-9030ϕ，电压u 滞后电流︒60（3）无法比较（4）︒=︒-︒=45-13590ϕ,电流1i 滞后电流2i ︒454.4 将以下正弦量转换为幅值相量和有效值相量，并用代数式、三角式、指数式和极坐标式表示，并分别画出相量图。

（1）u=310sint+90 V ω︒（） （2）i=10cos t A ω （3）u=1002sin t+30 V ω︒（）解：（1）().90m 31031090310310cos90sin90j U ej ︒==∠︒==︒+︒().9022022090220220cos90sin90j U ej ︒==∠︒==︒+︒相量图略（2）()10sin 90i t ω=+︒().901010901010cos90sin90j m I e j j ︒==∠︒==︒+︒ ().905252905252cos90sin90j I e j j ︒==∠︒==︒+︒相量图略（3）().3010021002301002cos 30sin 30506502j e j j m U ︒==∠︒=︒+︒=+()5025030sin 30cos 1003010010030.j j e U j +=︒+︒=︒∠==︒相量图略4.5 将以下相量转换为正弦量（1）50+j50U = （）V （2）m-30+j40I = （）A （3）j30m1002U e ︒= V （4）()1-30I=∠︒A 解：（1）()502sin 45u t ω=+︒V（2）4502sin 180-3i t arctg ω⎛⎫=+︒ ⎪⎝⎭A （3）()1002sin 30u t ω=+︒V （4）()2sin 30i t ω=-︒A4.6 已知：012202sin(314120)u t V =-，022202cos(31430)u t V =+ (1)画出它们的波形及确定其有效值，频率f 和周期T ； (2)写出它们的相量和画出相量图，并决定它们的相位差；解：（1） 01()2202sin(314-120)V u t t = 波形图略有效值220V 频率50Hz 、周期0.02s002()2202cos(31430)V=2202sin(31460)V u t t t =++ 波形图略有效值220V 频率50Hz 、周期0.02s（2）01220-120U =∠0222060U =∠相量图略 相位差01804.7 电路如题4.7图所示，电压，用相量法求电阻的电流和吸收的有功功率。

正弦交流电路 习题参考答案一、填空题：1. 表征正弦交流电振荡幅度的量是它的 最大值 ；表征正弦交流电随时间变化快慢程度的量是 角频率ω ；表征正弦交流电起始位置时的量称为它的 初相 。

三者称为正弦量的 三要素 。

2. 电阻元件上任一瞬间的电压电流关系可表示为 u = iR ；电感元件上任一瞬间的电压电流关系可以表示为dtdi Lu =L ；电容元件上任一瞬间的电压电流关系可以表示为dtdu Ci CC =。

由上述三个关系式可得， 电阻 元件为即时元件； 电感 和 电容 元件为动态元件。

3. 在RLC 串联电路中，已知电流为5A ，电阻为30Ω，感抗为40Ω，容抗为80Ω，那么电路的阻抗为 50Ω ，该电路为 容 性电路。

电路中吸收的有功功率为 450W ，吸收的无功功率又为 600var 。

二、 判断题：1. 正弦量的三要素是指最大值、角频率和相位。

（错）2. 电感元件的正弦交流电路中，消耗的有功功率等于零。

（对）3. 因为正弦量可以用相量来表示，所以说相量就是正弦量。

（错）4. 电压三角形是相量图，阻抗三角形也是相量图。

（错）5. 正弦交流电路的视在功率等于有功功率和无功功率之和。

（错）6. 一个实际的电感线圈，在任何情况下呈现的电特性都是感性。

（错）7. 串接在正弦交流电路中的功率表，测量的是交流电路的有功功率。

（错）8. 正弦交流电路的频率越高，阻抗越大；频率越低，阻抗越小。

（错）三、选择题：1. 某正弦电压有效值为380V ，频率为50Hz ，计时始数值等于380V ，其瞬时值表达式为（ B ）A 、t u 314sin 380=V ；B 、)45314sin(537︒+=t u V ；C 、)90314sin(380︒+=t u V 。

2. 一个电热器，接在10V 的直流电源上，产生的功率为P 。

把它改接在正弦交流电源上，使其产生的功率为P /2，则正弦交流电源电压的最大值为（ D ）A 、7.07V ；B 、5V ；C 、14V ；D 、10V 。

欢迎阅读欢迎阅读习 题2.1 电流π10sin 100π3i t ⎛⎫=- ⎪⎝⎭，问它的三要素各为多少？在交流电路中，有两个负载，已知它们的电压分别为1π60sin 3146u t ⎛⎫=- ⎪⎝⎭V ，2π80sin 3143u t ⎛⎫=+ ⎪⎝⎭V ，求总电压u 的瞬时值表达式，并说明u 、u 1、u 2三者的相位关系。

解：(1)最大值为10（V ），角频率为100πrad/s ，初相角为-60°。

（2）1U 则=m U 100=u 2.2 （1）i 1（2）i 1（3）i 1（4）i 1解：（1（2）I （3）=I （4）设+=1I I I 2.12=I 2.3 （1）u =t V （2）5i =-sin(314t – 60o) A解：(1)U =10/0o (V) (2)mI =－5/－60o =5/180o －60o=5/120o (A) 2.4 已知工频正弦电压u ab 的最大值为311V ，初相位为–60°，其有效值为多少？写出其瞬时值表达式；当t =0.0025s 时，U ab 的值为多少？解：∵U U ab abm 2=欢迎阅读∴有效值2203112121=⨯==U U abmab (V) 瞬时值表达式为 ()︒-=60314sin 311t u ab (V)当t =0.0025S 时，5.8012sin(31130025.0100sin 311-=-=⎪⎭⎫ ⎝⎛-⨯⨯=πππU ab (V)2.5 题解：（所以U a 由图b所以U a 2.6 （1（2（3解：（2=P U R ==R U I （2）P （32.7 把L =51mH 的线圈（线圈电阻极小，可忽略不计），接在u t +60o) V 的交流电源上，试计算： （1）X L 。

（2）电路中的电流i 。

（3）画出电压、电流相量图。

解：（1）16105131423=⨯⨯==-fL X L π(Ω)欢迎阅读（2）︒-=︒︒==30/75.1390/1660/220L jX U I （A ） )30314sin(275.13︒-=t i （A ）（3）相量图如图所示。

第一章 直流电路 复习与考工模拟参考答案一、填空题1．12 V 、24 V 、36 V 2．5 W 3．2.178×108 J 4．并联 5．12 K Ω 二、选择题 1．D2．A3．D4．D5．C三、判断题1．× 2．× 3．× 4．√ 5．√ 四、分析与计算题1．0.01 A ；10 mA ；1.0×104 μA 2．（1）A 115（或0.45 A ）（2）5.6 KW •h （3）2.8元第二章 电容与电感 复习与考工模拟参考答案一、填空题 1．106；1012 2．耐压3．储能；磁场；电场 4．103；1065．电阻（或欧姆） 二、选择题 1．D2．A3．C4．B5．A三、判断题1．√2．×3．×4．√5．√四、简答题略第三章磁场及电磁感应复习与考工模拟参考答案一、填空题1．安培定则（或右手螺旋定则）2．安培；BIlF=3．软磁物质；硬磁物质；矩磁物质4．电磁感应现象5．楞次二、选择题1．B 2．A 3．C 4．A 5．B三、判断题1．√2．√3．√4．×5．×四、分析与作图题1．略2．电流方向：BADCB第四章单相正弦交流电复习与考工模拟参考答案一、填空题1．振幅（最大值或有效值）；频率（周期或角频率）；初相2．V220（或311 V）；s2.0；rad/s)02（或314πrad/s1003．有效值4．电压与电流同频同相；电压超前电流900；电流超前电压9005．正比；反比6．在电感性负载两端并联一容量适当的电容器二、选择题1．B 2．B 3．B 4．D 5．C三、判断题1．×2．√3．×4．×5．√ 6. ×7. ×四、分析与计算题1．最大值：10 A；有效值：A5；周期：0.2 s；频率：5 Hz；初相：150022．440 W3．（1）R＝6Ω；L＝25.5 mH （2）0.6第五章三相正弦交流电复习与考工模拟参考答案一、填空题1．线电压；相电压；相电压；线电压2．220 V；380 V3．3；等于4．使不对称负载获得对称的相电压5．3；等于二、选择题1．D2．C3．A4．B5． A三、判断题1．√2．√3．√4．√5．×四、分析与作图题1．星形和三角形两种；画图略2．星形联结承受220V相电压；三角形联结时则承受380V线电压。

《电路与磁路》第四章三相正弦交流电路一、填空题1.三相电源绕组的连接方式有_________和_________两种，而常用的是_________连接。

2.三相四线制供电系统中，三个线电压为三相________，三个相电压也为三相________。

3.三相四线制供电系统中，线电压在数值上等于相电压的__________倍；相位上，线电压__________于相应的相电压__________。

4.三相对称负载三角形连接时，线电流在数值上等于相电流的__________倍。

在相位上，线电流比相对应的相电流__________。

5.三相对称负载的定义是：__________相等、__________相等、__________相同。

6.三相不对称负载作星形连接时，中线的作用是使三相负载成为三个_________________电路，保证各相负载都承受对称的电源____________。

7.三相负载作星形连接有中线，则每相负载承受的电压为电源的________电压，若作三角形连接，则每相负载承受的电压为电源的________电压。

8.已知三相电源的线电压为380V，而三相负载的额定相电压为220V，则此负载应作________形连接，若三相负载的额定相电压为380V，则此负载应作________形连接。

9.三相负载的连接方法有____________和____________两种。

10.三相电动机绕组可以连成__________或__________；由单相照明负载构成的三相不对称负载，一般都连成__________。

11.某三相异步电动机，定子每相绕组的等效电阻为8Ω，等效阻抗为6Ω,现将此电动机连成三角形接于线电压为380V的三相电源上。

则每相绕组的相电压为__________V，相电流为__________A，线电流为__________A。

12.某三相异步电动机，每相绕组的等效电阻R＝8Ω，等效感抗X L＝6Ω，现将此电动机连成星形接于线电压380V的三相电源上，则每相绕组承受的相电压为__________V，相电流为__________A，线电流为__________A。

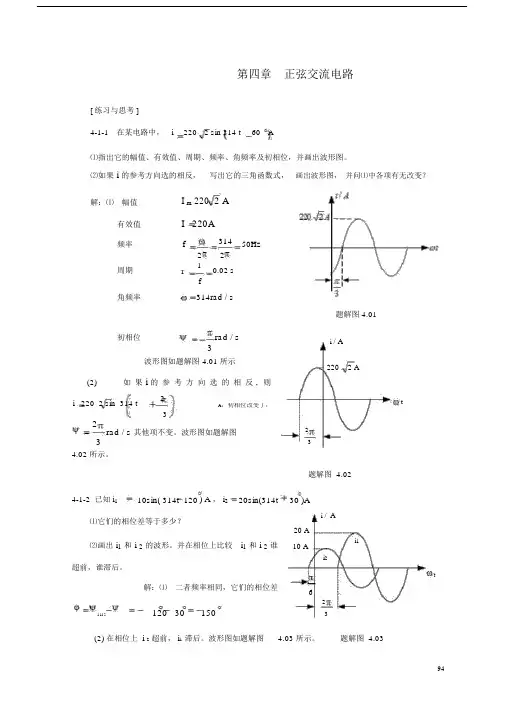
第四章正弦交流电路[ 练习与思考 ]4-1-1在某电路中，i 220 2 sin 314 t 60A⑴指出它的幅值、有效值、周期、频率、角频率及初相位，并画出波形图。

⑵如果 i 的参考方向选的相反，写出它的三角函数式，画出波形图，并问⑴中各项有无改变？解：⑴ 幅值I m 2202 A有效值I 220A频率f31450Hz22周期10.02 s Tf角频率314rad / s题解图 4.01初相位rad / s3波形图如题解图4.01 所示(2)如果 i 的参考方向选的相反,则i 220 2 sin 314 t 2A，初相位改变了，32rad / s 其他项不变。

波形图如题解图34.02 所示。

i / A220 2 At23题解图 4.024-1-2 已知i110sin( 314t 120) A ， i220sin(314t30 )A⑴它们的相位差等于多少？i /A20 Ai1⑵画出 i1和 i 2的波形。

并在相位上比较i1和 i 2谁10 Ai2超前，谁滞后。

t解：⑴ 二者频率相同，它们的相位差6120 301502i 1i 23(2) 在相位上i2超前，i1滞后。

波形图如题解图 4.03 所示。

题解图 4.034-2-1写出下列正弦电压的相量u1220sin ( t 45 )V ， u2100sin (314t 45 )V解：U1 110245V U2 50 2 45V4-2-2 已知正弦电流i18sin ( t60 )A 和 i2 6 sin ( t 30 )A ，试用复数计算电流i i1i2，并画出相量图。

解：由题目得到I m I m1I m28 60630+j(8 cos60j 8sin 60 )(6 cos30 6 sin30 )(4j 6.93)(5.2j 3)9.2j 3.931023.1 A所以正弦电流为I m 1I m 6023 .130+1 I m 2i110sin ( t 23.1 )A题解图 4.04相量图如题解图 4.04 所示。

习 题电流π10sin 100π3i t ⎛⎫=- ⎪⎝⎭，问它的三要素各为多少？在交流电路中，有两个负载，已知它们的电压分别为1π60sin 3146u t ⎛⎫=- ⎪⎝⎭V ，2π80sin 3143u t ⎛⎫=+ ⎪⎝⎭V ，求总电压u 的瞬时值表达式，并说明u 、u 1、u 2三者的相位关系。

解：(1)最大值为10（V ），角频率为100πrad/s ，初相角为-60°。

（2）︒-=30/601m U &（V ）︒=60/802mU &（V ） 则︒=︒+︒-=+=1.23/10060/8030/6021mm m U U U &&&（V ） )1.23314sin(100︒+=t u （V ）u 滞后u 2，而超前u 1。

两个频率相同的正弦交流电流，它们的有效值是I 1=8A ，I 2=6A ，求在下面各种情况下，合成电流的有效值。

（1）i 1与i 2同相。

（2）i 1与i 2反相。

（3）i 1超前i 2 90o 角度。

（4）i 1滞后i 2 60o 角度。

解：（1）146821=+=+=I I I （A ）（2）6821+=-=I I I （A ）（3）1068222221=+=+=I I I （A ）（4）设︒=0/81I &（A ）则︒=60/62I &（A ） ︒=︒+︒=+=3.25/2.1260/60/821I I I &&&（A ） 2.12=I （A ）把下列正弦量的时间函数用相量表示。

（1）u =t V （2）5i =-sin(314t – 60o) A解：(1)U &=10/0o (V) (2)mI &=－5/－60o =5/180o －60o=5/120o (A) 已知工频正弦电压u ab 的最大值为311V ，初相位为–60°，其有效值为多少？写出其瞬时值表达式；当t =时，U ab 的值为多少？解：∵U U ab abm 2=∴有效值2203112121=⨯==U U abm ab (V) 瞬时值表达式为 ()︒-=60314sin 311t u ab (V)当t =时，5.80)12sin(31130025.0100sin 311-=-=⎪⎭⎫ ⎝⎛-⨯⨯=πππU ab (V)题图所示正弦交流电路，已知u 1sin314t V ，u 2t –120o) V ，试用相量表示法求电压u a 和u b 。

图4-1 t rad f /3145014.322=⨯⨯==πωAt i Vt u )90314sin(2)45314sin(310︒-=︒+=︒=︒--︒=-=135)90(45i u ψψϕs T x 0075.0501360135360135=⨯︒︒=︒︒=25A t i i t A t t i f ）（，时，）（︒+=∴︒=∴===+=+⨯===3040sin 10305sin 10040sin 10)40sin(225402πψψψπψπππω︒∠=∠︒∠=︒∠=︒∠⨯︒∠=⋅+=+-+=-+=+++=+1.877.145657.51.53101.9857.5645657.51.531042)44()86(1210)44()86(21212121A A A A j j j A A j j j A A 2121)2(;)60sin(10,)sin(5)1(i i i A t i A t i +=︒+==ωω︒∠=︒∠+︒∠=+=︒∠=︒∠=∙∙∙∙∙89.4023.13601005)2(;6010,05)1(2121m m m m m I I I A I A I A I A I V U 25,10,22021===第四章习题4-1 已知正弦电压和正弦电流的波形如图4-1所示,频率为50Hz ，试指出它们的最大值、初相位以及它们之间的相位差，并说明哪个正弦量超前，超前多少度？超前多少时间？解： u 、i 的表达式为即：u 比i 超前135°，超前4-2 某正弦电流的频率为20Hz ，有效值为 A ，在t =0时，电流的瞬时值为5A ，且此时刻电流在增加，求该电流的瞬时值表达式。

解：4-3 已知复数A 1=6+j8Ω，A 2=4+j4Ω，试求它们的和、差、积、商。

解：4-4 试将下列各时间函数用对应的相量来表示。

解：4-5 在图4-2所示的相量图中，已知 ，它们的角频率是ω，试写出各正弦量的瞬时值表达式及其相量。

习题参考答案 A 选择题4.1.1 答案（2）提示：sin()m i I t ωψ=+ 依据题意sin3010m I = 4.1.2 答案（2）提示：100sin314100sin(314)u t t π=-=+ 10c o s 31410s i n (314)2i t t π==+ 4.2.1 答案（2）提示：向量表示中的三个要素 4.2.2 答案（1）提示：12340890490I I I I =++=∠︒+∠︒+∠-︒ 4.2.3 答案（2）提示：展开如30cos30jsin30∠︒=︒+︒ 4.3.1 答案（1）提示：jX j L L L L L U I I ω== 4.3.2 答案（3）提示：1j C CU I Cω= 4.3.3 答案（3）提示：j L LL U I X == 4.4.1 答案（2）提示：向量之比，有效值之比相互关系 4.4.2 答案（3）提示：1U II R jCω==- 注意加点不加点之区别4.4.3 答案（2） 提示：arctan L CX X Rϕ-=4.4.4 答案（1）提示：电路表现为纯电阻性，电流相位与电压相同。

4.4.5 答案（3） 提示：考虑1C X Cω=当电容C 增大对阻抗模以及幅角的影响。

4.5.1 答案（2）、（4）提示：A1、A2反向，//(jX )L C Z jX =- 4.5.2 答案（1） 提示：向量求解 4.5.3 答案（2）提示：//(jX )ab L C Z jX R =+- 4.7.1 答案（3）提示：RLC串联谐振频率0f = ，品质因数001LQ RCRωω==讨论电阻R 变化带来的影响4.7.2 答案（3）提示：分析方法与上题同。

B 基本题4.2.4 某实验中，在双踪示波器屏幕上显示出两个同频率正弦电压u 1和u 2的波形入图所示，（图略）（1）求电压u 1和u 2的周期和频率（2）若时间起点（t=0）选在图示位置，试写出u 1和u 2的三角函数式，并用向量式表示。

电工学少学时1-4章课后习题答案第一章电路的基本概念与基本定律11 电路和电路模型1、（1）实际电路是由各种电气器件按照一定的方式连接而成的，用于实现电能的传输、分配和转换，以及信号的传递、处理和控制等功能。

（2）电路模型是对实际电路的理想化和简化，它由理想电路元件组成，如电阻、电感、电容、电源等，用特定的符号表示，以便于对电路进行分析和计算。

2、常见的理想电路元件包括电阻元件、电感元件、电容元件、电压源和电流源。

电阻元件表示消耗电能并将电能转化为热能的元件；电感元件表示储存磁场能量的元件；电容元件表示储存电场能量的元件；电压源提供恒定的电压；电流源提供恒定的电流。

12 电流和电压的参考方向1、电流的参考方向是人为假定的电流流动的方向，若实际电流方向与参考方向相同，电流为正值；若实际电流方向与参考方向相反，电流为负值。

2、电压的参考方向也是人为假定的，通常从高电位指向低电位。

当实际电压方向与参考方向相同时，电压为正值；反之，电压为负值。

13 电功率和电能1、电功率是电路中单位时间内消耗或产生的电能，P ＝ UI。

当 P＞ 0 时，元件吸收功率；当 P ＜ 0 时，元件发出功率。

2、电能是电功率在一段时间内的积累，W ＝ Pt。

电能的单位通常是焦耳（J）。

14 电路元件1、电阻元件的伏安特性是一条通过原点的直线，其电阻值是常数。

2、电感元件的电压与电流的关系为：＄u ＝ L\frac{di}｛dt}＄。

3、电容元件的电流与电压的关系为：＄i ＝ C\frac{du}｛dt}＄。

15 电源元件1、理想电压源的端电压恒定不变，与通过它的电流无关。

2、理想电流源的输出电流恒定不变，其两端电压由外电路决定。

16 基尔霍夫定律1、基尔霍夫电流定律（KCL）：在任一时刻，流入一个节点的电流之和等于流出该节点的电流之和。

2、基尔霍夫电压定律（KVL）：在任一时刻，沿任一闭合回路，各段电压的代数和恒等于零。

第二章电路的分析方法21 电阻串并联连接的等效变换1、电阻串联时，等效电阻等于各个电阻之和，即＄R_{eq} ＝ R_1 ＋ R_2 ＋＼cdots ＋ R_n$。

主题4 正弦交流电路课题1 正弦交流电路的基本物理量一、判断题1．× 2．× 3．√ 4．√ 5．× 6．.× 7． × 8．× 9．√ 10．×二、选择题1．B 2．B 3．B 4．A 5．B 6．C 7．B 8．D 9．D三、填空题1．.正弦2．有效值，频率，初相3．方向4．50Hz ，0.02s5．V 2220 ，220V ，314rad/s ，314t+600，6006． mA 220，mA 240， 25×103Hz ， 450， -450， 40sin(157×103t+450) mA ， 80sin(157×103t-450) mA ，mA 220，mA 240-7．u U ϕ-∠8． -1200，i 2，i 19． V 240，V 230，600，-300，()V t 060sin 240+ω，()V t 030sin 230-ω，u 1超前u 2900四、简答题1． 矩形线圈在磁场中以ω角速度旋转产生交流电。

与直流电的区别：直流电的大小和方向不随时间变化，交流电的大小和方向均随时间变化。

让矩形线圈在磁场中以ω角速度旋转。

2．不能五、分析与计算1．(1)10A ，A 25，0.02s ，314rad/s ，1200， (2)()A i 350=，()A i 55-=，图略2． (1)0.408A3． V t e ⎪⎭⎫⎝⎛+⨯=43104sin 1006ππ，mA t i ⎪⎭⎫ ⎝⎛+=6sin 20πω，()V e 2500=，()mA i 100= 4． V E 010220∠=∙，V E 02120220-∠=∙，A I 01304-∠=∙，A I 02603∠=∙，图略5.略课题2 单相正弦交流电路的分析一、判断题1．× 2．× 3． √ 4． √ 5． × 6．×二、选择题1．.C 2．B 3．C 4．C 5．B 6．A 7．A 8．B三、填空题1．同相2．超前，2πf L ，Ω3．滞后， fc π21，Ω4．增大5．110，26．减小一倍7． 2Ω，1592μF8． tmA 314sin 2180，6.48W9． 10Ω，()A t 03120105sin 24.0-⨯，1.6var10． 10Ω，1.2A ，1.44var ，电流超前电压900四、简答题1．根据X L =2πf L 知，频率越高感抗越大2．根据fc X c π=21知，频率越高容抗越小五、分析与计算1． (1)44A ， (2) t i 314sin 244=，P=9680W ，图略2． (1)Im=1.58A ，I=1.12A ，()A t i 0120sin 58.1-=ω，(2) Q L =246.23var ，图略3． ()A t i c 0150314sin 245.3+=，Q C =759.8 var ，图略4． (1)tA i 314sin 222.0=，(2) P=48.4W ，图略5． (1) X L =50Ω，Q L =100 var ，()V t u 0460102sin 100+⨯=，(2) 略6． (1)C=450μF ，Q C =56.56var ，(2) 略课题3 RL 串联电路一、判断题1． √ 2．√ 3．√ 4． × 5． √ 6． √ 7． × 8．√ 9．√ 10． × 11．× 12． √ 13．√ 14．× 15． ×二、选择题1．A 2．C 3．B 4．B 5．A 6．A 7．B 8．A 9．C 10．B 11．C 12．B13．B三、填空题1．30Ω，127.4mH2．50V ，86.6V ，866var3．电源提供的总能量，V A4．ϕcos ⋅S ，ϕsin ⋅S ，22Q P +5．600，0.5，50W ，86.6var ，100var6．1，07．越小，越大8 ．66.27Kvar四、简答题1． 图略，电路中的电流将滞后电压一定的角度。

tωi /A222032πtωi /A 2032π6πA102i 1i 第四章 正弦交流电路[练习与思考]4-1-1 在某电路中，()A t i 60 314sin 2220-=⑴指出它的幅值、有效值、周期、频率、角频率及初相位，并画出波形图。

⑵如果i 的参考方向选的相反，写出它的三角函数式，画出波形图，并问⑴中各项有无改变？ 解：⑴ 幅值 A I m 2220有效值 A I 220= 频率 3145022f Hz ωππ===周期 10.02T s f== 角频率 314/rad s ω=题解图4.01 初相位 s rad /3πψ-=波形图如题解图4.01所示(2) 如果i 的参考方向选的相反, 则A t i ⎪⎭⎫ ⎝⎛+=32 314sin 2220π，初相位改变了，s r a d /32πψ=其他项不变。

波形图如题解图4.02所示。

题解图4.024-1-2 已知A )120314sin(101 -=t i ，A )30314sin(202 +=t i ⑴它们的相位差等于多少？⑵画出1i 和2i 的波形。

并在相位上比较1i 和2i 谁超前，谁滞后。

解：⑴ 二者频率相同，它们的相位差︒-=︒-︒-=-=1503012021i i ψψϕ (2)在相位上2i 超前，1i 滞后。

波形图如题解图4.03所示。

题解图4.03+1+j1m I ∙2m I ∙mI ∙︒60︒30︒1.234-2-1 写出下列正弦电压的相量V )45(sin 2201 -=t u ω，)V 45314(sin 1002 +=t u解：V U ︒-∠=∙4521101 V U︒∠=∙4525024-2-2已知正弦电流)A 60(sin 81 +=t i ω和)A 30(sin 62 -=t i ω，试用复数计算电流21i i i +=，并画出相量图。

解：由题目得到Aj j j j I I I m m m ︒∠=+=-++=︒-︒+︒+︒=︒-∠+︒∠=+=∙∙∙1.231093.32.9)32.5()93.64()30sin 630cos 6()60sin 860cos 8(30660821所以正弦电流为)A 1.23(sin 101 +=t i ω题解图4.04 相量图如题解图4.04所示。

图4-1 t rad f /3145014.322=⨯⨯==πωAt i Vt u )90314sin(2)45314sin(310︒-=︒+=︒=︒--︒=-=135)90(45i u ψψϕs T x 0075.0501360135360135=⨯︒︒=︒︒=25A t i i t A t t i f ）（，时，）（︒+=∴︒=∴===+=+⨯===3040sin 10305sin 10040sin 10)40sin(225402πψψψπψπππω︒∠=∠︒∠=︒∠=︒∠⨯︒∠=⋅+=+-+=-+=+++=+1.877.145657.51.53101.9857.5645657.51.531042)44()86(1210)44()86(21212121A A A A j j j A A j j j A A 2121)2(;)60sin(10,)sin(5)1(i i i A t i A t i +=︒+==ωω︒∠=︒∠+︒∠=+=︒∠=︒∠=•••••89.4023.13601005)2(;6010,05)1(2121m m m m m I I I A I A I A I A I V U 25,10,22021===第四章习题4-1 已知正弦电压和正弦电流的波形如图4-1所示,频率为50Hz ，试指出它们的最大值、初相位以及它们之间的相位差，并说明哪个正弦量超前，超前多少度？超前多少时间？解： u 、i 的表达式为即：u 比i 超前135°，超前4-2 某正弦电流的频率为20Hz ，有效值为 A ，在t =0时，电流的瞬时值为5A ，且此时刻电流在增加，求该电流的瞬时值表达式。

解：4-3 已知复数A 1=6+j8Ω，A 2=4+j4Ω，试求它们的和、差、积、商。

解：4-4 试将下列各时间函数用对应的相量来表示。

解：4-5 在图4-2所示的相量图中，已知 ，它们的角频率是ω，试写出各正弦量的瞬时值表达式及其相量。