平行圆柱体承受法向载荷时的接触应力分析

传递动力的高副机构，如摩擦轮、凸轮齿轮、链轮传动、滚动轴承、滚动螺旋等，都有接触强度问题，自然也涉及到接触应力。

在此对接触应力计算作较为全面的讨论。

两曲面的弹性体在压力作用下，相互接触时，都会产生接触应力，传递动力的高副机构在工作中往往出现的是交变应力，受交变接触应力的机器零件在一定的条件下会出现疲劳点蚀的现象，点蚀扩散到一定程度，零件就不能再用了，也就是说失效了，这样失效的形式称之为疲劳点蚀破坏，在ISO标准中是以赫兹应力公式为基础的。

本文较为集中地讨论了几种常见曲面的赫兹应力公式及常用机械零件的接触应力计算方法，便于此类零件的设计及强度验算。

1 任意两曲面体的接触应力1.1 坐标系图1所示为一曲面体的一部分，它在E点与另外一曲面体相接触，E点称为初始接触点。

取曲面在E点的法线为z轴，包括z轴可以有无限多个剖切平面，每个剖切平面与曲面相交，其交线为一条平面曲线，每条平面曲线在E点有一个曲率半径。

不同的剖切平面上的平面曲线在E点的曲率半径一般是不相等的。

这些曲率半径中，有一个最大和最小的曲率半径，称之为主曲率半径，分别用R′和R表示，这两个曲率半径所在的方向，数学上可以证明是相互垂直的。

平面曲线AEB所在的平面为yz平面，由此得出坐标轴x和y的位置。

任何相接触的曲面都可以用这种方法来确定坐标系。

由于z轴是法线方向，所以两曲面在E点接触时，z轴是相互重合的，而x1和x2之间、y1和y2之间的夹角用Φ表示(图2所示)。

图1 曲面体的坐标图2 坐标关系及接触椭圆1.2 接触应力两曲面接触并压紧，压力P沿z轴作用，在初始接触点的附近，材料发生局部的变形，靠接触点形成一个小的椭圆形平面，椭圆的长半轴a在x轴上，短半轴b在y轴上。

椭圆形接触面上各点的单位压力大小与材料的变形量有关，z轴上的变形量大，沿z轴将产生最大单位压力P0。

其余各点的单位压力P是按椭圆球规律分布的。

其方程为单位压力总压力P总＝∫PdF∫d F从几何意义上讲等于半椭球的体积，故接触面上的最大单位压力P0称为接触应力σH（1）a、b的大小与二接触面的材料和几何形状有关。

接触应力计算全面讨论图1 曲面体的坐标图2 坐标关系及接触椭圆1.2 接触应力两曲面接触并压紧，压力P 沿z 轴作用，在初始接触点的附近，材料发生局部的变形，靠接触点形成一个小的椭圆形平面，椭圆的长半轴a 在x 轴上，短半轴b 在y 轴上。

椭圆形接触面上各点的单位压力大小与材料的变形量有关，z 轴上的变形量大，沿z 轴将产生最大单位压力P 0。

其余各点的单位压力P 是按椭圆球规律分布的。

其方程为单位压力总压力 P 总＝∫PdF∫dF 从几何意义上讲等于半椭球的体积，故接触面上的最大单位压力P 0称为接触应力σH（1）a 、b 的大小与二接触面的材料和几何形状有关。

2 两球体的接触应力半径为R1、R2的两球体相互接触时，在压力P的作用下，形成一个半径为a的圆形接触面积即a＝b(图4)，由赫兹公式得式中：E1、E2为两球体材料的弹性模量；μ1、μ2为两球体材料的泊松。

图4 两球体外接触取综合曲率半径为R，则若两球体的材料均为钢时，E1＝E2＝E，μ1＝μ2＝μ＝0．3，则（2）如果是两球体内接触(图5)，综合曲率半径为，代入式(2)计算即可求出接触应力σH。

如果是球体与平面接触，即R2＝∞，则R＝R1代入式(2)计算即可。

图5 两球体内接触3 轴线平行的两圆柱体相接触时的接触应力轴线平行的两圆柱体接触时，变形前二者沿一条直线接触，压受力P 后，接触处发生了弹性变形，接触线变成宽度为2b 的矩形面(图6)，接触面上的单位压力按椭圆柱规律分布。

变形最大的x 轴上压力最大，以P 0表示，接触面上其余各点的压力按半椭圆规律分布，如图7，半椭圆柱的体积等于总压力P ，故图6 两圆柱体接触图7 轴线平行的两圆柱体相接触的压力分布最大单位压力（3）由赫兹公式知代入式(3)，得若两圆柱体均为钢时，E1＝E2＝E，μ1＝μ2＝0．3，取则接触应力为若为两圆柱体内接触(图8)，则以代入式(4)计算。

若是圆柱体与平面接触，则R2＝∞，R＝R1代入式(4)计算。

一. 是非题：正确的在（）中写“√”，错误的在（）中写“×”1、在不改变零件静强度的条件下,加大在一定载荷下零件的弹性变形量,将会降低该零件的冲击强度。

（ ）2、在不改变零件静强度的条件下，加大在一定载荷下零件的弹性变形量，可提高耐冲击强度。

（ ）3、设计零件时，安全系数应尽可能选大些，使该零件工作更可靠与安全。

（ ）4、某转轴采用40钢（σS MPa =335),经校核其扭转刚度不够，可改选高强度合金结构钢40Cr ()σS MPa =785，以提高刚度。

（ ）5、设计某普通碳钢零件时，校核后刚度不足，采用高强度合金钢时，对提高其刚度是不起作用的。

（ ）6、在变应力作用下，零件的主要失效形式将是疲劳断裂，而在静应力作用下，其失效形式将是塑性变形或断裂。

（ ）7、只要材料的平均极限应力σlim 大于零件的平均工作应力σm ，则安全系数S 就大于1，工作是可靠的。

（ ）8、若材料的平均极限应力σlim 大于零件的平均工作应力σm ，则零件的安全系数不一定总是大于1。

（ ）9、渐开线圆柱直齿轮传动空载运转时，可以认为是处于齿面线接触状态。

（ ）10、渐开线圆柱直齿轮传动工作时，齿面载荷的传递是通过真实的线接触进行的。

（ ）11、两圆柱体相接触，其轴线互相平行，在受法向压力作用下，则两零件的接触应力不等，直径大的零件所受接触应力小。

（ ）12、两圆柱体相接触，其轴线互相平行，受法向压力，则两零件的接触应力相等。

（ ）二、选择题：把正确的选项代号填入（）中1、在受轴向变载荷的紧螺栓联接中，采用柔性螺栓，是为了_____________。

A.增大变载荷下的剩余预紧力，提高联接可靠性；B.改善变载荷下的螺母支承面接触状态；C.降低应力幅σa；D.可减轻螺栓重量，节省材料。

2、已知某转轴在复合应力状态下工作，其弯矩作用与扭矩作用下的安全系数分别为Sσ=6.1，Sτ=18.5，则该转轴的实际安全系数大小为_____________________。

接触应力计算全面讨论传递动力的高副机构，如摩擦轮、凸轮齿轮、链轮传动、滚动轴承、滚动螺旋等，都有接触强度问题，自然也涉及到接触应力。

在此对接触应力计算作较为全面的讨论。

两曲面的弹性体在压力作用下，相互接触时，都会产生接触应力，传递动力的高副机构在工作中往往出现的是交变应力，受交变接触应力的机器零件在一定的条件下会出现疲劳点蚀的现象，点蚀扩散到一定程度，零件就不能再用了，也就是说失效了，这样失效的形式称之为疲劳点蚀破坏，在ISO标准中是以赫兹应力公式为基础的。

本文较为集中地讨论了几种常见曲面的赫兹应力公式及常用机械零件的接触应力计算方法，便于此类零件的设计及强度验算。

1 任意两曲面体的接触应力1.1 坐标系图1所示为一曲面体的一部分，它在E点与另外一曲面体相接触，E点称为初始接触点。

取曲面在E点的法线为z轴，包括z轴可以有无限多个剖切平面，每个剖切平面与曲面相交，其交线为一条平面曲线，每条平面曲线在E点有一个曲率半径。

不同的剖切平面上的平面曲线在E 点的曲率半径一般是不相等的。

这些曲率半径中，有一个最大和最小的曲率半径，称之为主曲率半径，分别用R′和R表示，这两个曲率半径所在的方向，数学上可以证明是相互垂直的。

平面曲线AEB所在的平面为yz平面，由此得出坐标轴x和y的位置。

任何相接触的曲面都可以用这种方法来确定坐标系。

由于z轴是法线方向，所以两曲面在E点接触时，z轴是相互重合的，而x1和x2之间、y1和y2之间的夹角用Φ表示(图2所示)。

半径为R1、R2的两球体相互接触时，在压力P的作用下，形成一个半径为a的圆形接触面积即a＝b(图4)，由赫兹公式得式中：E1、E2为两球体材料的弹性模量；μ1、μ2为两球体材料的泊松。

图4 两球体外接触取综合曲率半径为R，则若两球体的材料均为钢时，E1＝E2＝E，μ1＝μ2＝μ＝0．3，则（2）如果是两球体内接触(图5)，综合曲率半径为，代入式(2)计算即可求出接触应力σH。

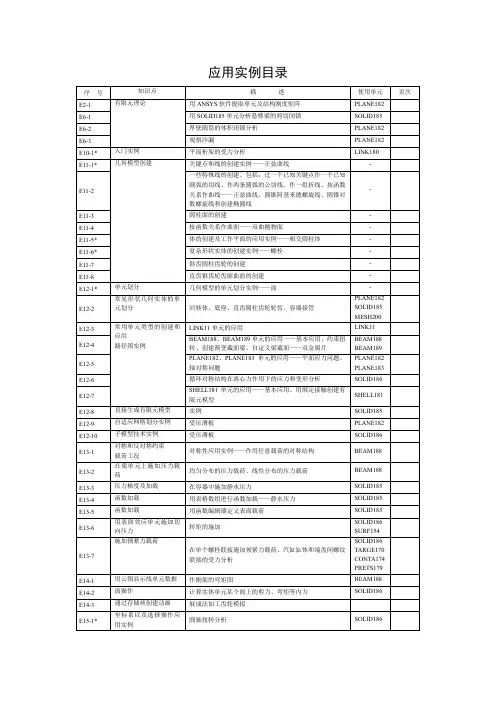
钢轮路轨接触应力核算报告1. 钢轮路轨接触应力核算将钢轮和路轨用一对轴线平行的圆柱体代替（路轨为半径无限大的圆柱体），ρ1、ρ2分别两圆柱的曲率半径，两圆柱体接触示意图见图1。

由弹性力学可知，当一对轴线平行的圆柱体相接触并受压力作用时，将由线接触变为面接触，其接触面为一狭长矩形，在接触面上产生接触应力，并且最大接触应力位于接触区中线上，根据赫兹公式[5]，其数值为：σH =√F n (1ρ1+1ρ2)πL(1−μ12E 1+1−μ22E 2)=Z E √F n LρεZ E =√1π(1−μ12E 1+1−μ22E 2)式中:σH :接触应力（Mpa ）； F n :法向力（N ）； L:接触线长度（mm ）；ρε:综合曲率半径（mm ）,ρε=ρ1ρ2ρ1±ρ2； ±:正号用于外接触，负号用于内接触；Z E :材料弹性系数，其中E 1、E 2分别为两圆柱体材料的弹性模量（MPa ）； μ1、μ2分别为两圆柱体材料的泊松比； 钢轮在路轨上行走，可简化为圆柱与平面接触。

单个行走轮承受最大静载（含拔模力）： F n =17500N 钢轮材质：45号钢调质； 轨道材质：Q345 钢轮宽度：L=65mm 钢轮半径：R=65mm ρε: 综合曲率半径（mm ）ρε=ρ1ρ2ρ1±ρ2=1（1ρ2+1ρ1）其中，钢轮的曲率半径：ρ1=R=65mm ，路轨的曲率半径：ρ2=∞ 代入求得综合曲率半径ρε=R=65 mm图1 两圆柱体接触示意图 Fig.3 Contact diagram of two cylinders钢轮及轨道材质泊松比：μ1=μ2=0.3钢轮及轨道材质弹性模量：E 1=E 2 =210000Mpa 45号钢调质以及Q345材质的屈服强度为σs =345Mpa最大接触应力σH ：Z E =√1π(1−μ12E 1+1−μ22E 2)=√1π(1−0.32210000+1−0.32210000) =191.7σH =Z E √F n Lρε=Z E √F n LR=191.69×√1750065×65=390.12Mpa ＞345Mpa所以钢轮直径R 选取65mm ，宽度L 选取65mm ，接触应力不满足使用要求。

一. 是非题：正确的在（）中写“√”，错误的在（）中写“×”1、在不改变零件静强度的条件下,加大在一定载荷下零件的弹性变形量,将会降低该零件的冲击强度。

（ ）2、在不改变零件静强度的条件下，加大在一定载荷下零件的弹性变形量，可提高耐冲击强度。

（ ）3、设计零件时，安全系数应尽可能选大些，使该零件工作更可靠与安全。

（ ）4、某转轴采用40钢（σS MPa =335),经校核其扭转刚度不够，可改选高强度合金结构钢40Cr ()σS MPa =785，以提高刚度。

（ ）5、设计某普通碳钢零件时，校核后刚度不足，采用高强度合金钢时，对提高其刚度是不起作用的。

（ ）6、在变应力作用下，零件的主要失效形式将是疲劳断裂，而在静应力作用下，其失效形式将是塑性变形或断裂。

（ ）7、只要材料的平均极限应力σlim 大于零件的平均工作应力σm ，则安全系数S 就大于1，工作是可靠的。

（ ）8、若材料的平均极限应力σlim 大于零件的平均工作应力σm ，则零件的安全系数不一定总是大于1。

（ ）9、渐开线圆柱直齿轮传动空载运转时，可以认为是处于齿面线接触状态。

（ ）10、渐开线圆柱直齿轮传动工作时，齿面载荷的传递是通过真实的线接触进行的。

（ ）11、两圆柱体相接触，其轴线互相平行，在受法向压力作用下，则两零件的接触应力不等，直径大的零件所受接触应力小。

（ ）12、两圆柱体相接触，其轴线互相平行，受法向压力，则两零件的接触应力相等。

（ ）二、选择题：把正确的选项代号填入（）中1、在受轴向变载荷的紧螺栓联接中，采用柔性螺栓，是为了_____________。

A.增大变载荷下的剩余预紧力，提高联接可靠性；B.改善变载荷下的螺母支承面接触状态；C.降低应力幅σa；D.可减轻螺栓重量，节省材料。

2、已知某转轴在复合应力状态下工作，其弯矩作用与扭矩作用下的安全系数分别为Sσ=6.1，Sτ=18.5，则该转轴的实际安全系数大小为_____________________。

圆柱壳开孔补强的接触应力分析魏化中1，2，黄柯2，舒安庆1，2【摘要】摘要：在压力容器开孔补强的薄壳理论分析中，通常假设在补强圈与容器壳体之间没有接触，接触应力对于结构应力分布的意义和影响尚不清楚。

应用ANSYS软件对内压作用下补强圈与壳体间接触行为进行有限元分析。

考察了接触变形和接触压力，探讨了补强圈与壳体间隙变化、刚度因子以及不同直径的接管对接触行为的影响。

相对于开孔补强的薄壳理论，文中更好地预测了补强圈与容器壳体间的应力场分布，得到了一些有参考价值的结论。

【期刊名称】管道技术与设备【年(卷),期】2009(000)006【总页数】3【关键词】开孔补强；有限元；接触；间隙0 引言圆柱壳开孔补强广泛应用于石油化工、电力等各个领域。

开孔后，由于容器壁被削弱且结构的连续性遭到破坏，在壳体和接管的连接处产生很高的局部应力，该区域最薄弱，最易发生失效。

因此，采用有效的补强措施来降低接管区的应力集中，从而提高整个容器的承载能力就具有重要的工程应用价值。

多年来，在压力容器的应力分析中，一直沿用经典的薄壳理论对开孔补强结构进行分析设计。

但这样的求解过程无法预测焊接区的应力以及补强圈与壳体间接触行为[1]。

有限元技术的发展，解决了上述问题。

应用ANSYS软件对补强圈与容器壳体间的接触行为进行模拟并分析接触压力的变化规律，从而为工程优化提供依据。

1 有限元模型的建立1.1 模型结构及尺寸补强圈按工程上常用的尺寸，即外径近似为接管直径的两倍。

有限元计算模型规格如下：筒体内径500 mm；接管长度150 mm；筒体长度350 mm；接管壁厚6 mm；筒体壁厚6 mm；补强圈外径250 mm；接管内径125 mm；内压5 MPa．1.2 有限元模型由于只考虑内压作用下的应力状况，因此有限元模型可利用结构的对称性取开孔接管区的1/4建模。

采用三维实体建模，采用8节点的SOLID45单元来模拟实体结构，用面-面三维接触单元TARGET170和CONTACT173来模拟其接触行为[2]。

传递动力的高副机构,如摩擦轮、凸轮齿轮、链轮传动、滚动轴承、滚动螺旋等,都有接触强度问题,自然也涉及到接触应力。

在此对接触应力计算作较为全面的讨论。

两曲面的弹性体在压力作用下,相互接触时,都会产生接触应力,传递动力的高副机构在工作中往往出现的就是交变应力,受交变接触应力的机器零件在一定的条件下会出现疲劳点蚀的现象,点蚀扩散到一定程度,零件就不能再用了,也就就是说失效了,这样失效的形式称之为疲劳点蚀破坏,在ISO 标准中就是以赫兹应力公式为基础的。

本文较为集中地讨论了几种常见曲面的赫兹应力公式及常用机械零件的接触应力计算方法,便于此类零件的设计及强度验算。

1 任意两曲面体的接触应力1、1 坐标系图1所示为一曲面体的一部分,它在E 点与另外一曲面体相接触,E 点称为初始接触点。

取曲面在E 点的法线为z 轴,包括z 轴可以有无限多个剖切平面,每个剖切平面与曲面相交,其交线为一条平面曲线,每条平面曲线在E 点有一个曲率半径。

不同的剖切平面上的平面曲线在E 点的曲率半径一般就是不相等的。

这些曲率半径中,有一个最大与最小的曲率半径,称之为主曲率半径,分别用R′与R 表示,这两个曲率半径所在的方向,数学上可以证明就是相互垂直的。

平面曲线AEB 所在的平面为yz 平面,由此得出坐标轴x 与y 的位置。

任何相接触的曲面都可以用这种方法来确定坐标系。

由于z 轴就是法线方向,所以两曲面在E 点接触时,z 轴就是相互重合的,而x 1与x 2之间、y 1与y 2之间的夹角用Φ表示(图2所示)。

图1 曲面体的坐标图2 坐标关系及接触椭圆1、2 接触应力两曲面接触并压紧,压力P沿z轴作用,在初始接触点的附近,材料发生局部的变形,靠接触点形成一个小的椭圆形平面,椭圆的长半轴a在x轴上,短半轴b在y轴上。

椭圆形接触面上各点的单位压力大小与材料的变形量有关,z轴上的变形量大,沿z轴将产生最大单位压力P0。

其余各点的单位压力P就是按椭圆球规律分布的。

接触应力不相等
接触应力是指两个物体接触时，由于法向压力和切向摩擦力的作用，在接触面上产生的应力。

接触应力的大小和分布取决于两个物体的形状、材料、表面粗糙度和接触方式等因素。

通常情况下，两材料不同的零件受力接触，其零件接触部位的接触应力不相等。

例如，大小两齿轮在啮合点处的接触应力是不相等的。

由于不同大小的齿轮具有不同的模数和齿数，导致啮合点处的接触面积不同，进而产生不同的接触应力。

通常情况下，大齿轮的接触应力更小，而小齿轮的接触应力更大。

这是因为在啮合过程中，大齿轮的齿面更宽，分担了更多的载荷，因此接触应力相对较小；而小齿轮的齿面相对较窄，承受较大的载荷，导致接触应力相对较大。

两表面接触应力与载荷之间关系在工程学和材料学中，负载和应力是研究物体力学性质最重要的方面之一。

在很多情况下，物体有两个表面相互接触，这时候就需要了解表面接触应力与载荷之间的关系。

第一步骤：定义两表面接触应力和载荷对于两个表面之间的接触，我们可以定义表面接触应力为两表面上相互压缩的力。

这个力是单位面积的压力，常用符号为σ。

而载荷则是作用在物体上的外力，可以是重力、压力、拉力等。

载荷通常用符号F表示，单位是牛顿或磅。

第二步骤：理解表面接触应力和载荷之间的关系当两个表面接触时，载荷会在表面上产生应力。

这个应力会在表面之间传递，直到达到适当的平衡状态。

接触应力与载荷之间的关系可以用下面的公式表示：σ = F / A其中，A是表面面积，σ是接触应力。

要理解这个公式，可以将其应用于一个简单的例子。

例如，在拖拉机车轮和地面之间的接触面上，轮径的承受载荷会被分摊到轮边缘的表面上。

若假设轮子的重量为750千克，表面接触面积为0.0015平方米，则轮边缘的接触压力将是：σ = 7500 N / 0.0015 m² = 5×10^6 Pa这个值大得惊人，但是表明了接触表面上的应力与承载的载荷是成正比关系的。

如果减少了接触面积，那么承载的载荷就会集中在更小的面积上，这最终会导致需要更高的接触应力。

第三步骤：如何影响表面接触应力表面接触应力的大小可以受到不同因素的影响。

例如，它受到物体间几何形状和表面粗糙程度的影响。

即便在表面较为光滑的情况下，也会存在微小的几何形状变化，从而导致一定程度的表面粗糙度。

此外，材料硬度也会影响表面接触应力。

硬度更高的材料可以更好地抵抗压力和剪切力，从而产生更大的表面接触应力。

最后，表面润滑也会影响表面接触应力。

例如，使用润滑剂可以减少接触力，从而减小表面接触应力。

这样，就可以减少磨损，降低噪音和稳定性问题等。

综上所述，表面接触应力与载荷之间的关系是非常重要的，并且受到多个因素的影响。

两零件的材料和几何尺寸都不相同,以曲面接触受载时,两者的接触应力
在两个零件以曲面接触受载时，它们的接触应力取决于多个因素，包括施加的负载、接触表面的几何形状、材料特性、以及表面条件等。

接触表面的几何形状：接触应力会根据接触表面的几何形状而变化。

如果两个接触表面的几何形状非常复杂，可能需要使用有限元分析（FEA）等数值方法来确定接触应力。

材料特性：包括弹性模量、泊松比和剪切模量等，这些都会影响接触应力。

例如，弹性模量较高的材料在同样大小的负载下会产生更高的接触应力。

表面条件：包括表面粗糙度、加工方法和涂层等。

这些因素会影响实际接触面积，从而影响接触应力。

例如，表面越粗糙，实际接触面积可能越大，导致平均接触应力降低。

施加的负载：这是决定接触应力的最直接因素。

通常，接触应力与施加的负载成正比。

由于两零件的材料和几何尺寸都不相同，因此需要分别对每个零件进行详细的分析，以确定其各自的接触应力。

然后可以通过适当的安全系数等方法来确保零件在使用过程中不会因为过高的接触应力而损坏。

接触应力弯曲应力
接触应力和弯曲应力是在不同力学情境下描述的两种不同类型的应力。

●接触应力（Contact Stress）：接触应力是指在两个物体表面相互接触的区域内的应力。

这种应力通常出现在两个固体物体表面直接接触的地方，例如在机械齿轮、轴承、齿轮传动等设备中。

接触应力的计算涉及到接触面的几何形状、力的大小和方向、材料的弹性模量等因素。

在接触应力中，关注的是两个物体之间的相互作用。

●弯曲应力（Bending Stress）：弯曲应力是在物体受到外部弯曲力作用时，在横截面上产
生的应力。

这种应力通常出现在梁、悬臂、梁柱等结构中，当这些结构受到弯曲力时，横截面上的不同点承受不同的应力。

弯曲应力的计算与物体的几何形状、外部加载、材料的弹性模量和截面惯性矩等因素相关。

在弯曲应力中，关注的是物体内部不同位置的应力分布。

总体来说，接触应力和弯曲应力描述了不同应用场景下的应力状态，一个涉及到表面的相互接触，另一个涉及到结构的形变和受力。

这两种应力都是工程和材料力学中重要的概念，对于设计和分析结构和设备都具有重要意义。

圆柱导轨负荷是指在圆柱形导轨系统中，由于载体的垂直力、水平力或倾斜力作用于导轨上所产生的力。

这种负荷可以分为几种不同的类型：
1. 垂直负荷：这是由于重力作用在载体上产生的力，它垂直作用于导轨表面。

2. 水平负荷：当载体受到水平方向的力（如摩擦力、推进力等）时，会在导轨上产生水平方向的负荷。

3. 径向负荷：当负荷沿着导轨的半径方向作用时，称为径向负荷。

这种负荷通常是由于外部力的直接作用或者由于旋转部件产生的离心力。

4. 轴向负荷：如果负荷沿着导轨轴线方向作用，则为轴向负荷。

这种负荷常见于直线运动系统中的轴承和导轨。

5. 复合负荷：实际应用中，导轨往往同时承受多方向的负荷，这时称为复合负荷。

为了确保系统的稳定性和耐用性，设计圆柱导轨系统时需要考虑这些负荷对导轨材料、尺寸、形状以及支撑结构的影响。

通过计算预期的最大负荷和使用适当的公差和安全系数，工程师可以设计出既能承受预期负荷又能保持低摩擦和高精度的导轨系统。

此外，润滑也是减少导轨负荷影响、延长使用寿命的关键因素之一。