- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
= 0, f ( x, x ) = 0,则该点 若相平面中的某点,同时满足 x
dx = 0 0,为不定值,这类特殊点称为奇点。 相轨迹的斜率 dx
通过奇点的相轨迹不止一条,它是相轨迹曲线的交点。 二阶线性系统:奇点是唯一的,位于原点。 二阶非线性系统:奇点可能不止一个。
例: 二阶系统
x x0 x
相平面图 D C E
0
B
1 A
x
p
由图可知: (1)在各种初始条件下(任意一条相轨迹),系统都趋 向原点(0,0),说明原点是系统的平衡点,系统是稳定的。 (2)如果初始条件为: x(0)=1, (0) = 0 。则相应的 x 相轨迹为ABCDE0。系统的 瞬态响应为阻尼振荡形式, 最大超调量为p,稳态误差 为零。
x
dx 02 x dx x
相平面
析法求解微分方程比较困难,甚至不可能时,可 采用图解法绘制相平面图。它有: (1)等倾线法 (2)园弧近似法(略) 下面介绍等倾线法: 原理:任一曲线都可以用一系列足够短的折线来近似, 如果我们能用简便的方法求得相平面中任意一点相轨迹的斜 率,就能画出通过该点相轨迹的切线,并用它来近似该点及 其附近的相轨迹曲线。如果点取得足够密,就能用一系列的 切线来近似相轨迹曲线了。
x (t )
x
t 方程的解
x
作为平面的直角坐标,则 1.相轨迹:如果我们取 x 和 x 系统在每一时刻的 ( x , x ) 均相应于平面上的一点。当 t 变 化时,这一点在 x x 平面上将绘出一条相应的轨迹----相轨迹。它描述系统的运动过程。
2.相平面: x x 平面称为相平面。对于一个系统,初始条件 不同时,其方程的解也不同。因而针对不同的初始条件,可 以绘出不同的相轨迹。若以各种可能的状态作为初始条件, 则可得到一组相轨迹族。 3.相平面图:相平面及其上的相轨迹族组成的图形称为系统 的相平面图。它表示系统在各种初始条件下的 运动过程。
时,采用一次积分法得相轨迹方程作图 x
f ( x) 0 x
dx dx d 2 x dx dx x x 2 dt dt dx dt dx
dx f ( x )dx x
代入方程
两边一次积分,得相轨迹方程
x d x f ( x)dx
) f ( x, x ) f ( x, x x x ) f ( x, x ) f ( x, x
x
) ( x, x
0
) ( x, x
x
) 是 即 f ( x, x
条件。
x
的奇函数
----相轨迹对称于 x 轴的
轴 相轨迹对称于 x
3)若相轨迹对称于原 点,其条件是:对称点
二阶系统微分方程: 两个独立变量: 构成相平面
= f ( x, x ) x
位置量 速度量
x
x
x(0) x0 为相变量。给定初始条件 x(0) = x x, x 0
相变量
在相平面上的 x, x
0 ) ( x0 , x
运动坐标轨迹称为相轨迹。
x
x
0
相平面 相轨迹
例: 二阶系统为 解 方程不显含
02 x 0 作相平面图。 x
,由解析法有
dx 2 x 0 x 0 dx 2 一次积分 x d x 0 x dx
1 2 1 2 2 0 x c1 x 2 2
相轨迹方程为椭圆方程
2 2 2 x 0 x c2
作出该系统的相平面图。 2 d x 解: 因为 斜率方程
x(0) x0 (0) x 0 x
dx 2 x x dx dt
(0,10)
dx xx dx x
x
x
0
相平面
初值(0, 10)和(0, -10)。
(0,-10)
二、解析法作图 方程不显含 方程为 因为
x(t) 1 A B E 0 t C
D
可将其状态转化为转化 为时间响应曲线x(t)来验证如图所示
时间响应曲线
2 相轨迹的绘制方法
一、相轨迹的共同特性
1.相轨迹的对称性 相轨迹的对称性可以从对称点上相轨迹的斜率来判断。 设二阶系统的方程为:
改写为:
+ f (x, x )= 0 x
dx dx dx dx , x= = = x dt dx dt dx
2 x x 等倾线方程. 2
可见,等倾线为过原点、斜率为 2 ( 2 ) 的直线。 若给定系统参数: =0.5, =1.
1 x 则等倾线为: x 1
取不同的 值,求得等倾 线如右图所示: 若给定初始条件为A,则 可作出相轨迹为ABCDE ..... 注意:两等倾线之间用其平 均值来表示相轨迹。
1 相平面法的基本概念
设二阶系统的常微分方程如下:
= f ( x, x ) x
式中,
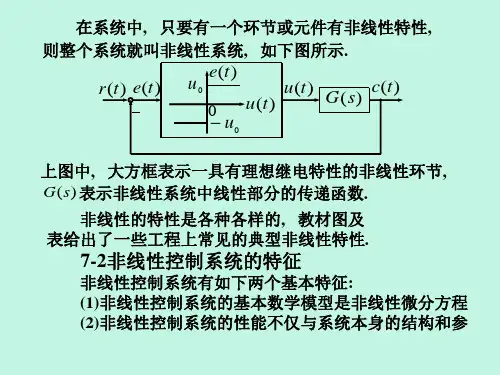
(t ) 的线性或非线性函数. ) 是 x (t ), x f ( x, x 由微分方程的理论可知,只要 f ( x, x ) 是解析的,那么在
给定的初始条件下,方程的解是唯一的。这个唯一的解可以 写成时间解的形式——x(t), 也可以写成以t为参变量的形式, = f ( x)来表示。 用x
二、线性系统的奇点与相轨迹 二阶线性系统的方程为:
2x 2x 0 x
可见,原点为奇点或稳定点。 由线性理论可知,系统的特征根不同,则其稳定性及瞬 态响应性能不同。在相平面中则表现为相轨迹的形状和奇点 性质不同。
奇点邻域的运动性质 由于在奇点上,相轨迹的斜率不定, 所以可以引出无穷条相轨迹。 相轨迹在奇点邻域的运动可以分为 1.趋向于奇点 2.远离奇点 3.包围奇点
dx x f x, x dx
dx f x, x dx = x 两边除以 可得: ----相轨迹的 dt dx x 斜率方程
1)若相轨迹对称于x轴。则在所有的对称点 ( x , x ) 和 ( x , x ) 上,相轨迹的斜率应大小相等,符号相反。即:
相平面法概述
相平面法是一种求解一、二阶常微分方程的图解法,即 二维状态空间法。这种方法的实质是将系统的运动过程形象 地转化为相平面上一个点的移动, 通过研究这个点移动的轨 迹, 就能获得系统运动规律的全部信息. 相平面法可以用来分析一、二阶线性或非线性系统的稳 定性、平衡位置、时间响应、稳态精度以及初始条件和参数 对系统运动的影响.
3 奇点与极限环
一、奇点 由前述可知,奇点是相平面中斜率不确定的点,即有 多条相轨迹以不同的斜率通过或逼近该点。
0 x 奇点必须同时满足: 奇点的求法 f(x, ) 0 x x 0 , 则 : 0 , x const 由于 x x
所以奇点是平衡点。奇点及临近的相轨迹反映了系 统的稳定性问题。
) f ( x, x f ( x, x ) x x
给定一个 α 值,可由上式求得一条等倾 线 ; 给定一组 α 值,则可求得一组等倾线族 , 它们确定了 相平面中相轨迹斜率的分布 .
2x 0 设系统方程为 : x 2 x dx dx dx dx 2 2 x x 0 上式改写为 : x x dx dt dx dt dx 令 代入上式 : dx 2 x 2x 0 x
= -1 A
x
B
=-1.4 =-1.6 C D E =-2 =-3 =∞ x =2 =1 =0
0
等倾线和相轨迹
所有通过等倾线的相轨迹都有相同的斜率
用等倾线绘制相轨迹时,必须注意以下几点:
1、为使导数 dx / dx 等于轨迹的几何斜率,必须对相平面上 轴采用相同的坐标比例。 的 x 轴和 x 2、相平面上,当 x 0 时,相轨迹的走向应沿着 x增加的 方向由左向右;当 x 0 时,相轨迹的走向应沿着 x 减 少的方向自右向左。 3、绘图时可利用相轨迹的对称性减少作图的工作量。 4、在斜率变化很快的区域,必须画出更多的等倾线,以 期改善作图的精确程度。
等倾线法作图步骤: 1)首先画出等倾线----确立相平面中相轨迹斜率的分布; 2)从初始条件开始,用连续的切线段来近似画出相轨迹曲线。 等倾线:在相平面中,相轨迹斜率相等的点的连线,即 等倾线应满足方程:
dx (常数 ) dx ) dx f ( x, x 由前述可知,相轨迹的斜率方程为: dx x 则等倾线方程为: ) f ( x, x f ( x, x ) x x
相平面分析方法: 由于相平面图表示了系统在各种初始条件下的运动过程, 因而,只要绘出了系统的相平面图,就可以用它来分析: 1)系统的稳定性; 2)瞬态响应性能; 3)稳态误差。 下面举二个例子进行说明:
例2-1.设系统的微分方程为:
x
+ x +x=0 x
其相平面图如右 图所示(绘制方法在 下节介绍) 图中的箭头表示 系统的状态沿相轨迹 的移动方向。
注意: 1)等倾线法在作图过程中会产生积累误差。一般来说, 等倾线越密,则近似程度越好。但等倾线过密,绘图条数增 多,致使积累误差加大。所以,一般间隔5°~10°画一条等 倾线较合适。 2)为减少作图误差,可事先在等倾线上画好表示切线 方向的平行短线,然后从初始状态开始逐步仔细地将它们联 成光滑的相轨迹曲线。 3)一般,线性系统的等倾线是直线。因此用等倾线法 比较方便。非线性系统的等倾线则有可能是曲线,甚至是比较 复杂的图形-----不适用于等倾线法。
x
) f ( x, x ) f ( x, x x x ) f ( x, x ) f ( x, x