当前位置：文档之家 › 弯曲应力习题课

弯曲应力习题课

  • 格式：ppt
  • 大小：1.55 MB
  • 文档页数：29

下载文档原格式

  / 29

合集下载

材料力学第2版 课后习题答案 第7章 弯曲变形

材料力学第2版 课后习题答案 第7章 弯曲变形

250
−qx l⎞ ⎛ 9l 3 − 24lx 2 + 16 x 3 ) ⎜ 0 ≤ x ≤ ⎟ ( 384 EJ 2⎠ ⎝ − ql ⎛l ⎞ y2 = −l 3 + 17l 2 x − 24lx 2 + 8 x 3 ) ⎜ ≤ x ≤ l ⎟ ( 384 EJ ⎝2 ⎠
y1 =
41ql 4 ( x = 0.25l ) 1536 EJ 5ql 4 ⎛l⎞ y⎜ ⎟ = − 768EJ ⎝2⎠
习 题 7-1 用积分法求图示各悬臂梁自由端的挠度和转角，梁的抗弯刚度EI为常量。
7－1 （a） M( x) = M 0
∴ EJy '' = M 0 1 EJy ' = M 0 x + C EJy = M 0 x 2 + Cx + D 2 边界条件: x = 0 时 y = 0 ； y' = 0
代入上面方程可求得：C=D=0
（c）
l−x q0 l q0 1 3 ⎛l−x⎞ M ( x) = − q( x) ( l − x ) ⎜ ⎟ = − ( l − x) 2 6l ⎝ 8 ⎠ q 3 ∴ EJy '' = 0 ( l − x ) 6l q 4 EJy ' = − 0 ( l − x ) + C 24l q 5 EJy = 0 ( l − x ) + Cx + D 120l y = 0 ； y' = 0 边界条件： x = 0 时 q( x) =
）
（c）解：
q0 x l q x2 EJy ''' = 0 + C 2l q0 x3 '' EJy = + Cx + D 6l q x 4 Cx 2 EJy ' = 0 + + Dx + A 24l 2 q0 x5 Cx 3 Dx 2 ' EJy = + + + Ax + B 120l 6 2 ⎧y=0 ⎧y=0 边界条件： x = 0 ⎨ '' x = l ⎨ '' ⎩y = 0 ⎩y = 0 ql D=0 ∴C = − 0 6 7q l 3 A= 0 B=0 360 EJy '''' =

刘鸿文《材料力学》复习笔记和课后习题(含考研真题)详解(弯曲应力)【圣才出品】

刘鸿文《材料力学》复习笔记和课后习题(含考研真题)详解(弯曲应力)【圣才出品】
W Iz bh3 / 12 bh2 h/2 h/2 6
对于圆形截面
W Iz πd 4 / 64 πd 3 d / 2 d / 2 32
对于环形截面
W D3 1 4 32
式中，α＝d/D，d为内径，D为外径。
2．弯曲正应力强度条件 σmax＝Mmax/W≤[σ] 强度条件的应用： ①强度校核 Mmax/W≤[σ] ②截面设计 W≥Mmax/[σ] ③确定许可载荷 Mmax≤W[σ]
8 / 71
圣才电子书 十万种考研考证电子书、题库视频学习平台

图 5-1-5 2．选择合理的截面（提高抗弯截面系数） （1）合理的截面形状应该是截面面积 A 较小，而抗弯截面系数 W 较大，常见截面的 W/A 值如表 5-1-2 所示。
FS I z b0
bh2 8
bh02 8
（3）翼缘主要承担了作用于工字形截面梁上的弯矩，通常不计算翼缘上的切应力。
5 / 71
圣才电子书 十万种考研考证电子书、题库视频学习平台

3．圆形截面梁 （1）切应力分布特点 边缘各点的切应力与圆周相切；y 轴上各点的切应力沿 y 轴，如图 5-1-3 所示。 （2）计算假设 AB 弦上各点的切应力作用线通过同一点 p；AB 弦上各点的切应力沿 y 轴的分量 y 相 等。

（1）变形几何关系：服从平面假设 应变分布规律：直梁纯弯曲时纵向纤维的应变与它到中性层的距离成正比。 （2）物理关系：满足胡克定律 应力分布规律：直梁纯弯曲时横截面上任意一点的正应力，与它到中性轴的距离成正比。 （3）静力关系 纯弯曲时，梁轴线变形后的曲率 1/ρ＝M/（EIz）。由于曲率 1/ρ 与 EIz 成反比，因此称 EIz 为梁的抗弯刚度。联立胡克定律：σ＝Ey/ρ 可得纯弯曲时正应力计算公式 σ＝My/Iz 式中，M为梁横截面上的弯矩；y为梁横截面应力计算点到中性轴的距离；Iz为梁横截 面对中性轴的惯性矩。 适用范围：①适用于任何横截面具有纵向对称面，且载荷作用在对称面内的情况；②公 式由等直梁得到，对缓慢变化的变截面梁和曲率很小的曲梁也近似成立。

材料力学习题

材料力学习题

材料力学作业册学院：专业：年级：班级：学号：姓名：前言本作业题册是为适应当前我校教学特色而统一筛选出来的题集，入选题目共计72个，教师可根据学时情况有选择性的布置作业。

本题册中列出的题目仅是学习课程的最基本的作业要求，老师根据情况可适当增加部分作业，部分学生如果有考研或者其他方面更高的学习要求，请继续训练其他题目。

本题册仅用于学生课程训练之练习，任何人不得将其用于商业目的，违者将追究其法律责任。

由于时间仓促，并限于编者水平有限，缺点和错误在所难免，恳请大家提出修改建议。

王钦亭wangqt@ 2013年2月27日目录第一章绪论 (1)第二章拉伸与压缩 (2)第三章扭转 (7)第四章弯曲应力 (11)第五章弯曲变形 (18)第六章简单超静定问题 (20)第七章应力状态与强度理论 (25)第八章组合变形与连接件计算 (32)第九章压杆稳定 (36)第十章能量法 (41)第十一章动荷载.交变应力 (49)附录I 截面的几何性质 (53)第一章绪论1-1 材料力学的中所讲的构件失效是指哪三方面的失效？1-2 可变形固体的基本假设有哪些？1-3 材料力学中研究的“杆”，有什么样的几何特征？1-4 材料力学中，杆件的基本变形有哪些？第二章 拉伸与压缩2-1（SXFV5-2-1）试求图示各杆1-1和2-2横截面上的轴力，并作轴力图。

2-2（SXFV5-2-2）一打入地基内的木桩如图所示，沿杆轴单位长度的摩擦力为2f kx （k 为常数），试作木桩的轴力图。

A2-3（SXFV5-2-3）石砌桥墩的墩身高=10 m l ，其横截面尺寸如图所示。

荷载 1 000 kN F =，材料的密度33=2.3510 kg/m ρ⨯。

试求墩身底部横截面上的压应力。

2-4（SXFV5-2-6）一木桩受力如图所示。

柱的横截面为边长200 mm 的正方形，材料可认为符合胡克定律，其纵向弹性模量10 GPa E =。

如不计柱的自重，试求： （1）作轴力图；（2）各段柱横截面上的应力； （3）各段柱的纵向线应变； （4）柱端A 的位移。

机械设计课后习题-答案

机械设计课后习题-答案

第三章 机械零件的强度p45习题答案3-1某材料的对称循环弯曲疲劳极限MPa 1801=-σ，取循环基数60105⨯=N ，9=m ，试求循环次数N分别为7 000、25 000、620 000次时的有限寿命弯曲疲劳极限。

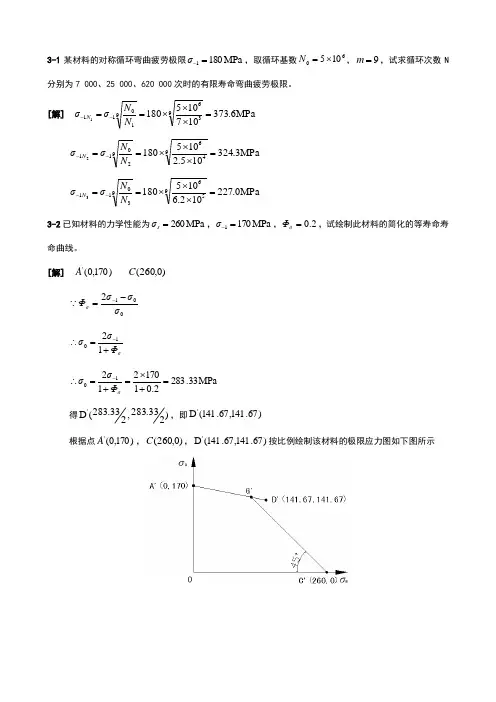
[解] MPa 6.373107105180936910111=⨯⨯⨯==--N N σσN MPa 3.324105.2105180946920112=⨯⨯⨯==--N N σσN MPa 0.227102.6105180956930113=⨯⨯⨯==--N N σσN 3-2已知材料的力学性能为MPa 260=s σ，MPa 1701=-σ，2.0=σΦ，试绘制此材料的简化的等寿命寿命曲线。

[解] )170,0('A )0,260(C 012σσσΦσ-=- σΦσσ+=∴-121MPa 33.2832.0117021210=+⨯=+=∴-σΦσσ得)233.283,233.283(D '，即)67.141,67.141(D '根据点)170,0('A ，)0,260(C ，)67.141,67.141(D '按比例绘制该材料的极限应力图如下图所示3-4 圆轴轴肩处的尺寸为：D =72mm ，d =62mm ，r =3mm 。

如用题3-2中的材料，设其强度极限σB =420MPa ，精车，弯曲，βq =1，试绘制此零件的简化等寿命疲劳曲线。

[解] 因2.14554==d D ，067.0453==d r ，查附表3-2，插值得88.1=ασ，查附图3-1得78.0≈σq ，将所查值代入公式，即()()69.1188.178.0111k =-⨯+=-α+=σσσq查附图3-2，得75.0=σε；按精车加工工艺，查附图3-4，得91.0=σβ，已知1=q β，则35.211191.0175.069.1111k =⨯⎪⎭⎫ ⎝⎛-+=⎪⎪⎭⎫ ⎝⎛-+=qσσσσββεK ()()()35.267.141,67.141,0,260,35.2170,0D C A ∴ 根据()()()29.60,67.141,0,260,34.72,0D C A 按比例绘出该零件的极限应力线图如下图3-5 如题3-4中危险截面上的平均应力MPa 20m =σ，应力幅MPa 20a =σ，试分别按①C r =②C σ=m ，求出该截面的计算安全系数ca S 。

工程力学(静力学和材料力学)第2版课后习题答案 范钦珊主编 第8章 弯曲刚度

工程力学(静力学和材料力学)第2版课后习题答案 范钦珊主编 第8章 弯曲刚度

课
后 答
案
网
解：由挠度表查得：
FP al 180° × 3 EI π Wal 180° = ⋅ 3 EI π 20000 × 1 × 2 × 64 180° = ⋅ 3 × 200 × 109 × π d 4 π ≤ 0 .5 ° d ≥ 0.1117 m，取 d = 112mm。
θB =
ww w
6 ( 246 + 48) ×10 × 200 ×10 × π × 32 × 10−12
2
co
m
8—3 具有中间铰的梁受力如图所示。试画出挠度曲线的大致形状，并说明需要分几段 建立微分方程，积分常数有几个，确定积分常数的条件是什么？（不要求详细解答）
习题 8－3 图
后 答
案
网
习题 8－4 图
课
习题 8－4a 解图
解： (a)题 1.
wA = wA1 + wA 2
wA1 =
⎛l⎞ q⎜ ⎟ ⎝2⎠
87图示承受集中力的细长简支梁在弯矩最大截面上沿加载方向开一小孔若不考虑应力集中影响时关于小孔对梁强度和刚度的影响有如下论述试判断哪一种是正确的
eBook
工程力学
（静力学与材料力学）
习题详细解答
(第 8 章) 范钦珊 唐静静
课
后 答
案
网
2006-12-18
ww w
1
.k hd
aw .
co
m
（教师用书）
−3 9 4
(
.k hd
解：由挠度表查得 F ba 2 wC = P l − a 2 − b2 6lEI
(
)
习题 8－9 图
8
aw .
)

机械设计(第八版)课后习题答案及解析(_参考答案及解析)

机械设计(第八版)课后习题答案及解析(_参考答案及解析)
⑤齿数比
⑥计算应力循环次数
⑦由图10-19取接触疲劳寿命系数
⑧计算接触疲劳许用应力
取失效概率为 ，安全系数
⑨由图10-26查得
⑩计算齿轮的圆周速度
计算尺宽与齿高之比
计算载荷系数
根据 ，8级精度，查图10-8得动载荷系数
由表10-3，查得
按轻微冲击，由表10-2查得使用系数
由表10-4查得 {按 =1查得}
（1）
工作应力点在疲劳强度区，根据变应力的循环特性不变公式，其计算安全系数
（2）
工作应力点在疲劳强度区，根据变应力的平均应力不变公式，其计算安全系数
5-3分析活塞式空气压缩气缸盖联接螺栓在工作时的受力变化情况，它的最大应力，最小应力如何得出当气缸内的最高压 力提高时，它的最大应力，最小应力将如何变化
⑧计算弯曲疲劳许用应力
取弯曲疲劳安全系数
⑨计算大、小齿轮的 ，并加以比较
取
⑩由弯曲强度确定的最大转矩
（4）齿轮传动的功率
取由接触强度和弯曲强度确定的最大转矩中的最小值
即
第十一章 蜗杆传动p272
习题答案
11-1试分析图11-26所示蜗杆传动中各轴的回转方向、蜗轮轮齿的螺旋方向及蜗杆、蜗轮所受各力的作用位置及方向。
[解]受力图如下图：
10-2如图，ABC的材料为中碳钢调制，其硬度：齿轮A为240HBS，B:260HBS，C:220HBS，试确定齿轮B的许用接触应力 和许用弯曲应力 .假定：1）齿轮B为“惰轮”（中间轮）齿轮A为主动轮，齿轮C为从动轮，设 ;2)齿轮B为在主动轮，齿轮A和齿轮C均为从动，设
10-3对于做双向传动的齿轮来说，她的齿面接触应力和齿根弯曲应力各属于什么循环特性在做强度计算时应怎么考虑

工程力学(静力学和材料力学)第2版课后习题答案 范钦珊主编 第7章 弯曲强度

工程力学(静力学和材料力学)第2版课后习题答案 范钦珊主编 第7章 弯曲强度

[ ]
[]
0.5 x 0.4125
M(kN.m)
7
习题 7－10 图
解：画弯矩图如图所示： 对于梁：
M max = 0.5q M 0.5q σ max = max ≤ [σ ] , ≤ [σ ] W W [σ ]W = 160 ×106 × 49 ×10−6 = 15.68 ×103 N/m=15.68kN/m q≤ 0.5 0.5
A
B
W
a + Δa
W + ΔW
B
A
a图
b图
整理后得
Δa =
ΔW (l − a ) (W + ΔW )
此即为相邻跳水者跳水时，可动点 B的调节距离 Δa 与他们体重间的关系。 7－ 14 利用弯曲内力的知识，说明为何将标准双杠的尺寸设计成 a=l/4。
9
习题 7－14 图
解：双杠使用时，可视为外伸梁。 其使用时受力点应考虑两种引起最大弯矩的情况。如图a、b所示。
[ ]＋
[σ ]－ ＝120 MPa。试校核梁的强度是否安全。
6
30 x 10 M(kN.m) C 截面
+ = σ max － σ max
40
习题 7－9 图
30 ×103 N ⋅ m × 96.4 ×10−3 m = 28.35 × 106 Pa=28.35 MPa 1.02 ×108 ×10−12 m 4 30 ×103 N ⋅ m ×153.6 ×10−3 m = = 45.17 ×106 Pa=45.17 MPa 1.02 ×108 × 10−12 m 4 40 ×103 N ⋅ m ×153.6 ×10−3 m = 60.24 ×106 Pa=60.24 MPa> [σ ] 8 −12 4 1.02 ×10 × 10 m 40 ×103 N ⋅ m × 96.4 × 10−3 m = = 37.8 × 106 Pa=37.8 MPa 8 −12 4 1.02 × 10 × 10 m

机械设计_吴昌林课后复习题答案(部分)

机械设计_吴昌林课后复习题答案(部分)

2-4 已知某钢制零件受弯曲变应力的作用，其中，最大工作应力σmax=200MPa，最小工作应力σmin=－50MPa，危险截面上的应力集中系数kσ=1.2，尺寸系数εσ=0.85，表明状态系数β=1。

材料的σs=750MPa，σ0=580MPa，σ-1=350MPa。

试求：（1）绘制材料的简化极限应力图，并在图上标出工作应力点的位置；（2）求材料在该应力状态下的疲劳极限应力σr；（3）按疲劳极限应力和安全系数分别校核此零件是否安全（取S min=1.5）An alloy steel part suffers bending stress：σs=750MPa，σ0=580MPa，σ-1=350MPaWorking stress：σmax=200MPa，σmin=－50MPakσ=1.2，εσ=0.85，β=1，(1) Make the stress endurance figure, and find the working point.(2) Find the fatigue stress limitation σr.(3) Check if this part is safe, using the fatigue stress limitation and the safety factor (if S min=1.5).Solution：1) calculate stress amplitude、mean stress and stress ratio2) judge where the working point is＝0.46∴working point is in AOD3) calculate endurance limit4) check strengthA. Allowable stressSafe！B. Safety factorSafe！3－3、3－6、3－83－3 A transmission with two pairs of gears is shown as problems figure 3-1. The axial forcesof the two gears on the axle II, Fa2 andFa3 are to be eliminated. The helix angleof the first pair of gears I＝15. Try todetermine the helix angle of the secondpair of gears, and the helix directions forthe gear 3 and gear 4 on it.Solution:(1) The torque of gear 2 and gear 3T2=9550000*P2/n2T3=9550000*P3/n3n2=n3, since the two gears are on the same axleP2=P3, when ignore the transfer efficiencySo that, T2=T3(2) The axial force of gear 2 equal to gear 3Fig3-22 Transmission with two pair of gears(P54, Helical gear , m n z must be divided by cos )so=0.172546 =9.94=9056’24’’3－6 An enclosed transmission with two pairs of gears. Known:P1=20kW, n1=1430r/min.Gear ratio u=4.3, one direction rotating.16 hour per day, and life is more than 5 years. With lower stiffness shaft and slight impact load.Material 40Cr, with surface hardening. Hardness:48～55HRC Complete the design for the first pair helical gear.Solution ：1）Determine the required materials and hardness of them. Compute the allowable stress. （1）Determine the required materials and hardness. 40Cr, with surface hardening.Hardness:48～55HRC, and use 55HRC.（2）Compute the allowable stress.① Determine the endurance limit stress.σH lim and σF lim Check the fig 3－16(c)，σH lim1=σH lim2=1200MPa Check the fig 3－17(c)，σF lim1=σF lim2=360MPa② Life cycle number N . Determine the life factor Z N 、Y NFrom fig 3－18，. From fig 3－19，.③Compute the allowable stress.From the table 3－4, 。

材料力学第五版课后习题答案详解

材料力学第五版课后习题答案详解

Microsoft Corporation材料力学课后答案[键入文档副标题]lenovo[选取日期]第二章轴向拉伸和压缩2-12-22-32-42-52-62-72-82-9下页2-1试求图示各杆1-1和2-2横截面上的轴力，并作轴力图。

（a）解：；；（b）解：；；（c）解：；。

(d)解：。

返回2-2 试求图示等直杆横截面1-1，2-2和3-3上的轴力，并作轴力图。

若横截面面积，试求各横截面上的应力。

解：返回2-3试求图示阶梯状直杆横截面1-1，2-2和3-3上的轴力，并作轴力图。

若横截面面积，，，并求各横截面上的应力。

解：返回2-4 图示一混合屋架结构的计算简图。

屋架的上弦用钢筋混凝土制成。

下面的拉杆和中间竖向撑杆用角钢构成，其截面均为两个75mm×8mm的等边角钢。

已知屋面承受集度为的竖直均布荷载。

试求拉杆AE和EG横截面上的应力。

解：=1）求内力取I-I分离体得（拉）取节点E为分离体，故（拉）2）求应力75×8等边角钢的面积A=11.5 cm2(拉)（拉）2-5(2-6)图示拉杆承受轴向拉力，杆的横截面面积。

如以表示斜截面与横截面的夹角，试求当，30，45，60，90时各斜截面上的正应力和切应力，并用图表示其方向。

解：2-6(2-8) 一木桩柱受力如图所示。

柱的横截面为边长200mm的正方形，材料可认为符合胡克定律，其弹性模量E=10 GPa。

如不计柱的自重，试求：（1）作轴力图；（2）各段柱横截面上的应力；（3）各段柱的纵向线应变；（4）柱的总变形。

解：（压）（压）。

第七章-弯曲应力(1) (2)

第七章-弯曲应力(1) (2)
y
M
z

Q
横截面上内力 横截面上切应力

横截面上正应力
Q dA
A
M y dA
A
切应力和正应力的分布函数不知道，2个方程确定不了
切应力无穷个未知数、正应力无穷个未知数，实质是 超静定问题 解决之前，先简化受力状态 —— 理想模型方法
8
横力弯曲与纯弯曲 横力弯曲 ——
剪力Q不为零 （ Bending by transverse force ） 例如AC, DB段
E
A
(-) B
D
(+) 10kN*m
y2
C
拉应力
a
e
压应力
y1
压应力 B截面
b
d
拉应力 D截面
危险点：
a, b, d
33
（3）计算危险点应力 拉应力
a
e
压应力
校核强度
M B y2 a Iz 30 MPa （拉） M B y1 b Iz
70 MPa （压）
压应力 B截面
b
d
强度问题 弯曲问题的整个分析过程： 弯曲内力 弯曲应力 弯曲变形 刚度问题
5
本章主要内容
7.1 弯曲正应力 7.2 弯曲正应力强度条件 7.3 弯曲切应力及强度条件 7.4 弯曲中心 7.5 提高弯曲强度的一些措施
这一堂课先效仿前人，探求出来弯曲正应力
公式，然后解决弯曲正应力强度问题
6
知道公式会用，不知推导，行不行？不行。
2
解：1 画 M 图求有关弯矩
qLx qx M1 ( ) 2 2
2
2
x 1
60kNm
M max qL / 8 67.5kNm

孙训方《材料力学》(第6版)笔记和课后习题(含考研真题)详解-弯曲问题的进一步研究(圣才出品)

孙训方《材料力学》(第6版)笔记和课后习题(含考研真题)详解-弯曲问题的进一步研究(圣才出品)

cos
=
−
1 8
ql 2
cos
= − 1 2103 N/m(4.2 m)2 cos 20o 8
= −4144 N m
My
=
−M
sin
=
−
1 8
ql 2
sin
= − 1 2103 N/m(4.2 m)2 sin 20o 8
= −1508 N m
A、B 点坐标分别为：
yA＝80mm，zA＝（b－z0）＝45mm，yB＝－80mm，zB＝－18mm
10.2 课后习题详解 10-1 截面为 16a 号槽钢的简支梁，跨长 l＝4.2m，受集度为 q＝2kN/m 的均布荷 载作用。梁放在 φ＝20o 韵斜面上，如图 10-2-1 所示。若不考虑扭转的影响，试确定梁危 险截面上 A 点和 B 点处的弯曲正应力。
4 / 20
圣才电子书 十万种考研考证电子书、题库视频学习平台
A
=
−
1508 Ngm 73.310−8 m4
45 10−3
m
−
4144 Ngm 866.2 10−8 m4
80
10−3
m=
−131
MPa
点 B 处有最大拉应力
( ) ( ) B
=
−
1508 Ngm 73.310−8 m4
−1810−3 m
−
4144 Ngm 866.2 10−8 m4
−80 10−3 m
一、非对称纯弯曲梁的正应力 当梁不具有纵向对称面，或者梁虽具有纵向对称平面，但外力不作用在该平面时，梁将 发生非对称弯曲。非对称纯弯曲梁正应力计算公式见表 10-1-1。
表 10-1-1 非对称纯弯曲梁正应力计算公式

孙训方材料力学第五版课后习题答案详细讲解

孙训方材料力学第五版课后习题答案详细讲解

Microsoft Corporation训方材料力学课后答案[键入文档副标题]lenovo[选取日期]第二章轴向拉伸和压缩2-12-22-32-42-52-62-72-82-9下页2-1 试求图示各杆1-1和2-2横截面上的轴力，并作轴力图。

（a）解：；；（b）解：；；（c）解：；。

(d) 解：。

返回2-2 试求图示等直杆横截面1-1，2-2和3-3上的轴力，并作轴力图。

若横截面面积，试求各横截面上的应力。

解：返回2-3试求图示阶梯状直杆横截面1-1，2-2和3-3上的轴力，并作轴力图。

若横截面面积，，，并求各横截面上的应力。

解：返回2-4 图示一混合屋架结构的计算简图。

屋架的上弦用钢筋混凝土制成。

下面的拉杆和中间竖向撑杆用角钢构成，其截面均为两个75mm×8mm的等边角钢。

已知屋面承受集度为的竖直均布荷载。

试求拉杆AE和EG横截面上的应力。

解：=1）求力取I-I分离体得（拉）取节点E为分离体，故（拉）2）求应力75×8等边角钢的面积A=11.5 cm2(拉)（拉）2-5(2-6) 图示拉杆承受轴向拉力，杆的横截面面积。

如以表示斜截面与横截面的夹角，试求当，30，45，60，90时各斜截面上的正应力和切应力，并用图表示其方向。

解：2-6(2-8) 一木桩柱受力如图所示。

柱的横截面为边长200mm的正方形，材料可认为符合胡克定律，其弹性模量E=10 GPa。

如不计柱的自重，试求：（1）作轴力图；（2）各段柱横截面上的应力；（3）各段柱的纵向线应变；（4）柱的总变形。

解：（压）（压）返回2-7(2-9) 一根直径、长的圆截面杆，承受轴向拉力，其伸长为。

试求杆横截面上的应力与材料的弹性模量E。

解：2-8(2-11) 受轴向拉力F作用的箱形薄壁杆如图所示。

已知该杆材料的弹性常数为E，，试求C与D两点间的距离改变量。

解：横截面上的线应变相同因此返回2-9(2-12) 图示结构中，AB为水平放置的刚性杆，杆1，2，3材料相同，其弹性模量E=210GPa，已知，，，。

工程力学课后习题答案第9章题解g

工程力学课后习题答案第9章题解g

−
a)
对应的最大正应力
σ2
=
M2 Wz
=
F(l − a) / 4 Wz
据题意有σ 2 = [σ ]，及
σ 1 − σ 2 ×100% = 30% σ2
将σ 1 ,σ 2 的值代入，得
Fl / 4 − F (l − a) / 4
Wz
Wz
F(l − a) / 4
= 0.3
Wz
整理得
70
a = 0.3 l = 0.231l = 0.231× 6 = 1.39 m 1.3
1 qa 2 2
=
0，F
=
P 3
，q
=
P l
即
Pa − 1 ⋅ P a 2 = 0 ， a = 2 l
3 2l
3
（2） M (x) = Fx − 1 qx2 = P x − P x2
2
3 2l
M ′(x) = 0 ， P − P x = 0 ， x = 2
3l
3
M ⎜⎛ l ⎟⎞ = P ⋅ l − 1 ⋅ P ⋅ ⎜⎛ l ⎟⎞2 = Pl ⎝ 3 ⎠ 3 3 2 l ⎝ 3 ⎠ 18
因此，辅助梁应有的最小跨长为：1.39 m 。 9-8 一桥式起重机梁 跨 l = 10.5 m ，横截面 为 36a 工字钢。已知 梁 的许用应力
[σ ] = 140 MPa ，电葫芦自重 12 kN，当起吊重量为 50 kN 时，梁的强度不够。为满足正应 力强度要求，在梁中段的上、下各焊一快钢板，如图。求加固钢板的最小长度 l0 。
(a）
(b)
( ) 解 ∑ M A = 0 ， FB = 7.64 kN ↑ ( ) ∑ Fy = 0 ， FA = 3.36 kN ↑

机械设计课后习题答案

机械设计课后习题答案

第三章 机械零件的强度 p45习题答案3-1 某材料的对称循环弯曲疲劳极限σ1 180MPa ，取循环基数 N 0 5 106，m 9 ，试求循环次数 N 分别为7 000 、 25 000、620 000 次时的有限寿命弯曲疲劳极限。

σs 260MPa ，σ1 170MPa ，Φσ 0.2 ，试绘制此材料的简化的等寿命寿命曲线。

[解 ] A '(0,170)C(260,0)得D '(283.332,283.332)，即 D '(141.67,141 .67)根据点 A '(0,170) ， C (260,0) ， D '(141.67,141.67) 按比例绘制该材料的极限应力图如下图所示3-4 圆轴轴肩处的尺寸为： D=72mm ，d=62mm ，r=3mm 。

如用题 3-2 中的材料，设其强度极限σB=420MPa ，精 车，弯曲， βq =1，试绘制此零件的简化等寿命疲劳曲线。

D54 r 3 ［解］ 因D54 1.2， r 3 0.067 ，查附表 3-2，插值得σ1.88 ，查附图 3-1 得q σ0.78 ，将所查d45 d 45σσ值代入公式，即查附图 3-2，得 εσ 0.75 ；按精车加工工艺，查附图 3-4，得 βσ 0.91，已知 βq 1，则 根据 A 0,72.34 ,C 260,0 ,D 141.67,60.29 按比例绘出该零件的极限应力线图如下图3-5 如题 3-4 中危险截面上的平均应力 σm 20MPa ，应力幅 σa 20MPa ，试分别按① r C ② σm C ，求 出该截面的计算安全系数 S ca 。

［解］ 由题 3-4可知 σ-1 170MPa, σs 260MPa, Φσ 0.2,K σ 2.35（ 1） r C 工作应力点在疲劳强度区，根据变应力的循环特性不变公式，其计算安全系数 （ 2） σm C工作应力点在疲劳强度区，根据变应力的平均应力不变公式，其计算安全系数3-2 已知材料的力学性能为 [解 ]σ1N 15 1067 103180 373.6MPa第五章螺纹连接和螺旋传动p101习题答案5-1 分析比较普通螺纹、管螺纹、梯形螺纹和锯齿形螺纹的特点，各举一例说明它们的应用5-2 将承受轴向变载荷的联接螺栓的光杆部分做得细些有什么好处？答：可以减小螺栓的刚度，从而提高螺栓联接的强度。

No.20 习题课(钢结构)

No.20 习题课(钢结构)

主讲：何嘉年
第3章 钢结习构题的复连习接课
第21页
若有侧焊缝，又有端焊缝， 则先求端焊缝受力
N3

2
0.7h f
b
1 .2 2
f
w f
再求侧焊缝受力
N1

k1 N

N3 2
N2

k2 N

N3 2
1

N1 2 0.7 h f ( l h f
)

f
w f
2

N2 2 0.7 h f ( l h f
主讲：何嘉年
第5页
习题复习课
焊缝剪应力为：


N cos560 lwt
1500 103 cos560 583 10
144MPa
fvw
180MPa
满足承载力要求
土木与交通工程学院 School of Civil and Transportation Engineering
主讲：何嘉年
何嘉年第19页习题复习课弯曲引起最大的应力剪力引起的应力v98kn计算焊缝最不利点的应力最不利点在a点处可以偏安全地认为弯曲由焊缝群承担剪力由竖向焊缝平均承担土木与交通工程学院schooltransportationengineering主讲
钢结构设计原理
课后习题复习课
焊缝连接计算
习题复习课
1. 通过一、二级检验的对接焊缝的强度可以
主讲：何嘉年
第7页
习题复习课
3.10 有一支托角钢，两边用角焊缝与柱相连，如图 所示，钢材为Q345A，焊条为E50型，手工焊，Ⅱ级 焊缝的质量检验标准，试确定焊缝高度（焊缝有绕 角，焊缝长度可以不减去2hf）。 已知：外力N=400kN。

第五章 弯曲应力

第五章 弯曲应力

★
2 、措施
提高弯曲强度的措施
1）减小M（合理按排梁的受力情况）:支座
★
2 、措施
提高弯曲强度的措施
1）减小M（合理按排梁的受力情况）：布载
★
2 、措施
提高弯曲强度的措施
2） 增大W（合理截面）：矩形
★
2 、措施
提高弯曲强度的措施
2） 增大W（合理截面）：工字形、槽形、矩形、
圆形比较（W/A值）
习题讨论课
2）不同材料
组合截面梁
c
Ac
hc
sc
∑Fx=0
σt=Ety/ρ σc=Ecy/ρ
t
s d A = F
A
N
At
ht
t
st
FN=0
c
中性轴？
At
s dA s
Ac
dA = 0
习题讨论课
2）不同材料
c
Ac
hc
组合截面梁
sc
∑My=0
At
ht
t
st
( E ) zdA = 0
例（书例5-1)
★ 横力弯曲时的正应力
※ 弯曲强度特点
1)危险面往往有几处 2)同一截面危险点往往不只一个
★ 横力弯曲时的正应力
※ 有些材料 s t s c 拉压强度要分别校核
s t max
M s t = W t z max
M s c = W c z max
★
2 、措施
提高弯曲强度的措施
2） 增大W（合理截面）：注意和思考 a) 工艺成
本（如空心截面） b) 考虑材质（如铸铁T形梁等）
★

材料力学第5章弯曲应力

材料力学第5章弯曲应力
材料力学第5章弯曲应力
欢迎来到材料力学第5章弯曲应力的世界！在本章中，我们将深入探讨什么是 弯曲应力，并研究其在不同形状截面中的计算方法和应用。
弯曲应力的定义和概念
什么是弯曲应力？
弯曲应力是物体受到外力作用时，在横截面上产生的力分布状态。
应变张量与应力张量
了解应变张量和应力张量的关系是理解弯曲应力的基础。
应力-应变曲线与弯曲应力
探索材料的应力-应变曲线与弯曲应力之间的关系。
弯曲应力在工程中的应用
建筑结构
了解弯曲应力在建筑结构中的应 用，如桥梁和楼梯等。
机械设计
探索弯曲应力在机械设计中的重 要性，如机械零件和工具。
航空航天工程
了解弯曲应力在航空航天工程中 的关键应用，如飞机和火箭。
梯形截面
探索梯形截面的弯曲应力计算方法。
弯曲应力的影响因素
1 外力
外力的大小和方向将直接影响到物体的弯曲应力。
2 截面形状
不同形状的截面将对弯曲应力的分布产生影响。
3 材料的力学性质
材料的弯曲应力极限和应力-应变关系是必须考虑的因素。
材料的弯曲应力极限
如何确定材料的弯曲应力极限
了解如何通过实验和模拟来确定材料的弯曲应力极限。
材料力学中的弯曲应力方程
一般弯曲应力方程
通过一般弯曲应力方程，我们可以计算出材料在弯曲时 的应力。
悬臂梁的弯曲应力
悬臂梁的弯曲应力方程与一般情况下的方程有所不同， 的弯曲应力计算方法
1
圆形截面
2
了解计算圆形截面的弯曲应力的公式和步骤。
3
矩形截面
学习如何计算矩形截面的弯曲应力。

材料力学第五版课后习题答案修订版

材料力学第五版课后习题答案修订版

材料力学第五版课后习题答案Company number：【WTUT-WT88Y-W8BBGB-BWYTT-19998】二、轴向拉伸和压缩2-1试求图示各杆1-1和2-2横截面上的轴力，并作轴力图。

（a）解：；；（b）解：；；（c）解：；。

(d)解：。

2-2 试求图示等直杆横截面1-1，2-2和3-3上的轴力，并作轴力图。

若横截面面积，试求各横截面上的应力。

解：2-3试求图示阶梯状直杆横截面1-1，2-2和3-3上的轴力，并作轴力图。

若横截面面积，，，并求各横截面上的应力。

解：2-4 图示一混合屋架结构的计算简图。

屋架的上弦用钢筋混凝土制成。

下面的拉杆和中间竖向撑杆用角钢构成，其截面均为两个75mm×8mm的等边角钢。

已知屋面承受集度为的竖直均布荷载。

试求拉杆AE和EG横截面上的应力。

解：=1）求内力取I-I分离体得（拉）取节点E为分离体，故（拉）2）求应力75×8等边角钢的面积A=11.5 cm2(拉)（拉）2-5(2-6)图示拉杆承受轴向拉力，杆的横截面面积。

如以表示斜截面与横截面的夹角，试求当，30，45，60，90时各斜截面上的正应力和切应力，并用图表示其方向。

解：2-6(2-8) 一木桩柱受力如图所示。

柱的横截面为边长200mm的正方形，材料可认为符合胡克定律，其弹性模量E=10 GPa。

如不计柱的自重，试求：（1）作轴力图；（2）各段柱横截面上的应力；（3）各段柱的纵向线应变；（4）柱的总变形。

解：（压）（压）2-7(2-9)一根直径、长的圆截面杆，承受轴向拉力，其伸长为。

试求杆横截面上的应力与材料的弹性模量E。

解：2-8(2-11)受轴向拉力F作用的箱形薄壁杆如图所示。

已知该杆材料的弹性常数为E，，试求C与D两点间的距离改变量。

解：横截面上的线应变相同因此2-9(2-12) 图示结构中，AB为水平放置的刚性杆，杆1，2，3材料相同，其弹性模量E=210GPa，已知，，，。

梁的弯曲计算—弯曲正应力的计算(工程力学课件)

梁的弯曲计算—弯曲正应力的计算(工程力学课件)
x(轴线)
横截面上σ的分布规律
My
Iz
横截面对中性轴的惯性矩
bh3 Iz 12
横截面对中性轴的惯性矩
bh3 Iz 12
Iz
D4 64
(14 )
My
Iz
式中各量均以绝对值代入！ σ的正负自己判断
【例 1】求梁固定端A的右侧截面上的指定点的正应力
40kN.m
c 0
A
B
a
M ya Iz
40 106 N mm 300 2
33.75 107 mm4
mm 17.78 MPa
（拉应力）
b
M yb Iz
40 106 N mm 75 mm 33.75107 mm4
8.88
MPa
（拉应力）
d
M yd Iz
40 106 N mm 300
2 33.75 107 mm4
mm 17.78 MPa
a
M ya Iz
76106 90 48.6 106
140.74MPa
（拉应力）
b
M yb Iz
76106 50 48.6 106
78.19MPa
（拉应力）
d
M yd Iz
76106 90 48.6 106
140.74MPa （压应力）
c 0
（压应力）
习题1：求悬臂梁固定端A的右侧截面上各点的正应力
76kN.m
20kN/m
18kN
58kN
（1）求支座反力 （2）画弯矩图
76
28
A
M图(kN m) B
习题1：求悬臂梁固定A
B
（3）求正应力
Iz
100 1803
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

A
1 2 3 1 2a 3
q
mB
C
2
B
YB
a
（a）
a
解：现用设正法 1）求1-1截面上Q1、M 1 用截面1 1截取梁左段为研究对象。如图（b）所示，设 截面上作用有正向Q1、M 1，O为截面形心。由静力平衡条件
Y qa Q
1
0 q a
答案： B
A
0.89kN
1kN m
C
D
E F
2kN
B
1.11kN
1.5m
1.5m
1.5m
3. 梁受力如图，剪力图和 弯距图正确的是（ ）。
P
P P
a
Pa
2a
a
（A）
P
Q Q Q
Pa Pa Pa Pa
M M M M
（B）
P
P
（C）
P
P P
Pa Pa
P
P
（D）
解：在熟练掌握作Q、M图方法的基础上，有时可将多个 载荷共同作用下的梁，按载荷分成几个简单基本的梁， 分别作Q、M图后加以叠加而得出总Q、M图。现将图示 梁（a）分成梁（b）与梁（c）。 梁（b）的外力是对称的，画出的Q图是反对称的，M图 是对称的。
（a）
m Pa
2P
A
C
B
a
2P
a
P
B
YB P
1 q0 l 6

C
l/ 3

1 q0 l 3
Q
b
M图（图（c））M A 0，M B 0，M x 为三曲线， 由dQ/dx Q x 可知，M x 的斜率开始为正值，越来越
趋 于0 正
小，经0（C面）变成负的，绝对值越来越大，它使M曲 线形成“上凸”（在规定M 坐标下）的三次曲线。在C 面（x l / 3）弯距取极值 1 l 1 q0 l 1 2 M 极 q0l q l 0 6 3 6 l 3 9 3 1 1 ） Q max = q0l，（x l）； M max q0l 2 （x l / 3）。 6 9 3
3 3
M3 Q3
4）取右段平衡求Q3、M 3 为此应先由整梁平衡（见图（a））求出固定端约束力 1 YB 2qa，mB qa 2。取右段，设正后（注意此时Q3、 2 q M 3的正值方向）如图（e） Q3 a Y Q q 2qa 0 3 M3 B 2 a/2 Y B Q3 qa (e) a a a 1 mO ( F ) M 3 q 2qa qa 2 0 2 4 2 2 3 M 3 qa 2 8 结果与取左段相同，符合同一截面上两侧的内力为 作用反作用关系。因此4）也可作为步骤3）所得结果 正确性的校核。
4.平面弯曲是指梁的横截面变形前是平面， 受力变弯后仍为平面的弯曲。 （ ）

答案：
变形后轴线所在平面与外力所在纵向平面相
重合的弯曲
四、计算题
1.梁受力如图（a）所示，求1-1，2-2，3-3面上的剪力 与弯距。其中1-1面与2-2面分别在紧靠外力偶m作用面C 的左则与右则。
qa
m 2qa2
Q
P
M
x
Pa
2 Pa
3Pa
x
（b） （c）
3.简支梁受线性分布载荷作用如图（a)所示，试作 Q、M图，并写出 Q max 、 M
max
。
q x
1 R q0l 6
q0
A
x
YA 1 q0l 6
B
x
l /3
l
1 YB q0l 3
a
解：1）求支承约束力 1 此时可视为分布载荷的合力R= q0 （三角形分布载荷为距 l 2 2 形分布之半）作用与x l处，设A、B处有约束力YA、YB。 3 2 1 m A F R l YB l 0， YB q0l 3 3 1 1 m B F R l YA l 0， YB q0l 3 6 1 1 1 校核 Y q0l q0l q0l 0 3 6 2
（A）（a x 2a），（a x 2a） （C）（a x 2a），（a x 2a）
A
（B）（a x 2a），（a x 2a） （D）（a x 2a），（a x 2a）
m
C
B
2m
D
x
a
a
YB = 3m 2a
a
答案： C
YA =
3m 2a
2.梁受力如图所示，指kN定截面C、D、E、F上正确的 Q、M 值应为（ ）。 （A）QC 0.89kN,M C 0.89 1.5 1 2.335kN m （B）QD 0.89kN,M D 0.89 1.5 1 0.335kN m （C）QE 1.11kN,M E 1.111.5 1.665kN m （D）QF 1.11kN,M F 1.111.5 1.665kN m
2)求2-2截面上Q2、M 2 取截面，设正后研究对象受力如图（c）
Y qa Q
Q2 qa M 2 qa 2
qa
2qa 2
2
0
A
a
(c )
2 O 2
M2
mO ( F ) M 2 qa a 2qa 2 0
2h
h 2
答案： A
h 2
h
h 2
h h
I I I Z Z1 Z 2
I Z2 I ZC a2 A
2b
（a）
h
2b
（b）
2b
（c）
三、判断题
1.在集中力作用处，梁的剪力图要发生突变，弯距图的斜率 要发生突变。
答案：
2.在Q=0处，弯距必取 M max 。
（ ）
（ ）
答案： 悬臂梁受均布荷载 3.钢梁与铝合金梁具有相同的横截面形状和尺寸，在相同 的弯距作用下将产生同样大在最大正应力。 （ ） 答案：
3
小
负值， 因为剪 力向下
c
C
1 9 3
M
q0l 2
4.用叠加法求图（a）所示梁的Q、M图， 并写出 Q max 、 M
max
。
2P
m Pa
A
C
B
a
（a）
a
梁（c）在A端作用有力偶m。切忌将AB整梁的剪力看成 零，弯距为M=m。这是忽略了约束力（步骤上忘了求约 P P 束力）的错误结果，求约束力YA （向下）。 YB 2 2 （向上）后的结果如图示。
）给定分段面（控制面）上Q、M 值并连线作图 根据AC、CB段Q x P，知Q图为一水平线（图（b））。 AC段M x Px，M A M O 0，M C左 M 2a 2 Pa 弯距图为一斜直线（斜率为 P）。CB段 x PxPa， M C右 M 2a Pa，M B左 3Pa，弯距图为一斜直线（斜 率也为-P），得M图如图（c）。
Q
Pa
答案： D
4.纯弯梁的横截面形状、尺寸如图（a）、（b）、（c）所示。 h 它们都是在2b 2h的矩形内对称于y轴挖空一个面积为b 的 2 小矩形。在相同弯距作用下，它们最大弯曲正应力大小的排 序是（ ）。 （A）（a）>（b）>（c） （C）（a）<（b）<（c） y b （B）（b）>（a）>（c） （D）（b）<（a）<（c） y y b b
A
Q1 qa mO ( F ) M 1 qa a 0 M 1 qa 2
弯矩为负值
Q1
a
(b )
O1
M1
Q1为负值，说明它实际方向向上。同时，按剪力 +、-号规定也应为负值，说明它实际转向为顺时针， 按弯距+、-号规定也应为负值。
a
作Q、M图 1 1 Q图（图（b）） Q A右 q0l，Q B左 q0l，Q x 为二次 3 6 曲线。它区别于直线，应取底三个控制面。可由Q x 0 得x l / （ 3 QC =0），由dQ/dx q x (), 知Q x 的斜率由A 面的0开始一直取负值至B面的 q0，Q图为“上凸”的二 次曲线。
b
4.图示横截面为等腰梯形的纯弯梁受弯距M 作用，已知 B 3b、h 2b则最大弯曲拉应力与最大弯曲压应力之比 （ max）（ ）。 t / max） c为（
5 答案： 7
M
b h
B
二、选择题
1.图示梁CB段的剪力、弯距方程为Q （x）=-3m / 2a， 3mx M （x）= m，其相应的适用区间分别为（ ）。 2a
3 3
mB
2.列方程作图（a）所示梁的剪力图与弯距图
P
m Pa
mB 3Pa
A x
x
2a
C
B
2a
x
YB P
（a）
P
m Pa
mB 3Pa
A
x
C
B
2a
x
YB P
x
2a
（a）
解：如图（a）建x轴，列方程作Q、M图的步骤如下： 1）求支承约束力 用整梁平衡条件求得YB P、mB 3Pa（图（ a））。 2）列Q x 、M x 方程 AC段Q x P （0<x 2a） M x Px （0 x<2a） CB段Q x P （2a x<4a） M x PxPa （2a<x<4a）
Q2
对Q2的说明同1 ）；M 2为正值，说明它实际转向与所设 相同，即逆时针，按弯距+、-号规定也应为正值。