第11章材料力学弯曲应力练习题

材料力学作业册学院：专业：年级：班级：学号：姓名：前言本作业题册是为适应当前我校教学特色而统一筛选出来的题集，入选题目共计72个，教师可根据学时情况有选择性的布置作业。

本题册中列出的题目仅是学习课程的最基本的作业要求，老师根据情况可适当增加部分作业，部分学生如果有考研或者其他方面更高的学习要求，请继续训练其他题目。

本题册仅用于学生课程训练之练习，任何人不得将其用于商业目的，违者将追究其法律责任。

由于时间仓促，并限于编者水平有限，缺点和错误在所难免，恳请大家提出修改建议。

王钦亭wangqt@ 2013年2月27日目录第一章绪论 (1)第二章拉伸与压缩 (2)第三章扭转 (7)第四章弯曲应力 (11)第五章弯曲变形 (18)第六章简单超静定问题 (20)第七章应力状态与强度理论 (25)第八章组合变形与连接件计算 (32)第九章压杆稳定 (36)第十章能量法 (41)第十一章动荷载.交变应力 (49)附录I 截面的几何性质 (53)第一章绪论1-1 材料力学的中所讲的构件失效是指哪三方面的失效？1-2 可变形固体的基本假设有哪些？1-3 材料力学中研究的“杆”，有什么样的几何特征？1-4 材料力学中，杆件的基本变形有哪些？第二章 拉伸与压缩2-1（SXFV5-2-1）试求图示各杆1-1和2-2横截面上的轴力，并作轴力图。

2-2（SXFV5-2-2）一打入地基内的木桩如图所示，沿杆轴单位长度的摩擦力为2f kx （k 为常数），试作木桩的轴力图。

A2-3（SXFV5-2-3）石砌桥墩的墩身高=10 m l ，其横截面尺寸如图所示。

荷载 1 000 kN F =，材料的密度33=2.3510 kg/m ρ⨯。

试求墩身底部横截面上的压应力。

2-4（SXFV5-2-6）一木桩受力如图所示。

柱的横截面为边长200 mm 的正方形，材料可认为符合胡克定律，其纵向弹性模量10 GPa E =。

如不计柱的自重，试求： （1）作轴力图；（2）各段柱横截面上的应力； （3）各段柱的纵向线应变； （4）柱端A 的位移。

材料⼒学专项习题练习弯曲应⼒弯曲应⼒1. 圆形截⾯简⽀梁A 、B 套成，A 、B 层间不计摩擦，材料的弹性模量2B A E E =。

求在外⼒偶矩e M 作⽤下，A 、B 中最⼤正应⼒的⽐值maxminA B σσ有4个答案： (A)16； (B)14； (C)18； (D)110。

答：B2. 矩形截⾯纯弯梁，材料的抗拉弹性模量t E ⼤于材料的抗压弹性模量c E ，则正应⼒在截⾯上的分布图有以下4种答案：答：C3. 将厚度为2 mm 的钢板尺与⼀曲⾯密实接触，已知测得钢尺点A 处的应变为11000-，则该曲⾯在点A 处的曲率半径为 mm 。

答：999 mm4. 边长为a 的正⽅形截⾯梁，按图⽰两种不同形式放置，在相同弯矩作⽤下，两者最⼤正应⼒之⽐max a max b ()()σσ= 。

答：2/15. ⼀⼯字截⾯梁，截⾯尺⼨如图，, 10h b b t ==。

试证明，此梁上,下翼缘承担的弯矩约为截⾯上总弯矩的88%。

证：412, (d ) 1 8203B A z z zMy M Mt M y yb y I I I σ==?=?? 4690z I t =, 41411 82088%3690M t M t =??≈B t A M =+=为翼缘弯矩(a)6. 直径20 mm d =的圆截⾯钢梁受⼒如图，已知弹性模量200 GPa E =, 200 mm a =，欲将其中段AB 弯成 m ρ=12的圆弧，试求所需载荷，并计算最⼤弯曲正应⼒。

解：1M EIρ= ⽽M Fa = 4840.78510 m , 0.654 kN 64d EI I F aπρ-==?==33max 80.654100.220102220.78510M d Fad I I σ--====??7. 钢筋横截⾯积为A ，密度为ρ，放在刚性平⾯上，⼀端加⼒F ，提起钢筋离开地⾯长度/3l 。

试问F解：截⾯C 曲率为零2(/3)0, 326C Fl gA l gAlM F ρρ=-==8. 矩形截⾯钢条长l ，总重为F ，放在刚性⽔平⾯上，在钢条A 端作⽤/3F 向上的拉⼒时，试求钢条内最⼤正应⼒。

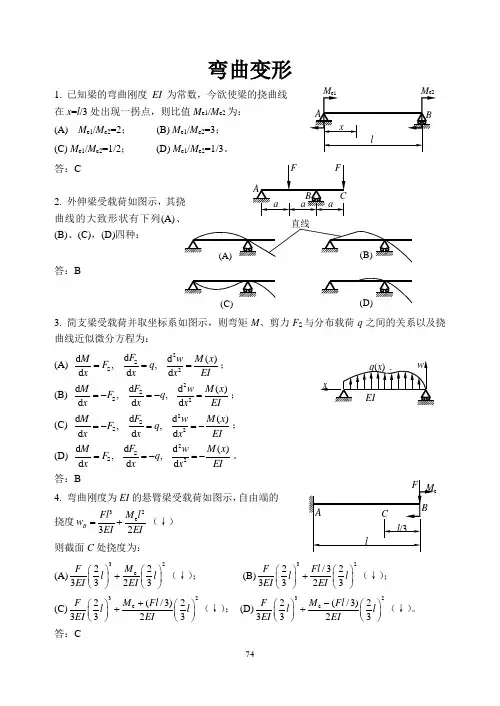
弯曲变形1. 已知梁的弯曲刚度EI为常数，今欲使梁的挠曲线在x=l/3处出现一拐点，则比值M e1/M e2为：(A) M e1/M e2=2；(B) M e1/M e2=3；(C) M e1/M e2=1/2；(D) M e1/M e2=1/3。

答：C2. 外伸梁受载荷如图示，其挠曲线的大致形状有下列(A)、(B)、(C)，(D)四种：答：B3. 简支梁受载荷并取坐标系如图示，则弯矩M、剪力F S与分布载荷q之间的关系以及挠曲线近似微分方程为：(A)2SS2dd d(),,d d dFM w M xF qx x x EI===；(B)2SS2dd d(),,d d dFM w M xF qx x x EI=-=-=；(C)2SS2dd d(),,d d dFM w M xF qx x x EI=-==-；(D)2SS2dd d(),,d d dFM w M xF qx x x EI==-=-。

答：B4. 弯曲刚度为EI的悬臂梁受载荷如图示，自由端的挠度23e32BM lFlwEI EI=+（↓）则截面C处挠度为：(A)32e223323MFl lEI EI⎛⎫⎛⎫+⎪ ⎪⎝⎭⎝⎭（↓）；(B)322/323323F Fll lEI EI⎛⎫⎛⎫+⎪ ⎪⎝⎭⎝⎭（↓）；(C)32e(/3)223323M FlFl lEI EI+⎛⎫⎛⎫+⎪ ⎪⎝⎭⎝⎭（↓）；(D)32e(/3)223323M FlFl lEI EI-⎛⎫⎛⎫+⎪ ⎪⎝⎭⎝⎭（↓）。

答：C5. 画出(a)、(b)、(c)三种梁的挠曲线大致形状。

答：6. 试画出图示梁的挠曲线大致形状。

答：7. 正方形截面梁分别按(a)、(b)两种形式放置，则两者间的弯曲刚度关系为下列中的哪一种： (A) (a)＞(b)； (B) (a)＜(b)； (C) (a)=(b)； (D) 不一定。

答：C8. 试写出图示等截面梁的位移边界条件，并定性地画出梁的挠曲线大致形状。

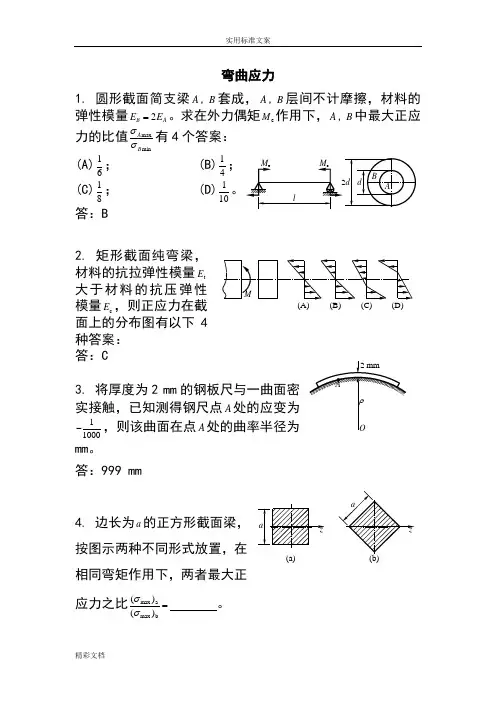
(A)(B)(C)(D)弯曲应力1. 圆形截面简支梁A,B套成，A,B层间不计摩擦，材料的弹性模量2B AE E=。

求在外力偶矩e M作用下，A,B中最大正应力的比值maxminABσσ有4个答案：(A)16； (B)14；(C)18； (D)110。

答：B2. 矩形截面纯弯梁，材料的抗拉弹性模量tE大于材料的抗压弹性模量cE，则正应力在截面上的分布图有以下4种答案：答：C3. 将厚度为2 mm的钢板尺与一曲面密实接触，已知测得钢尺点A处的应变为11000-，则该曲面在点A处的曲率半径为mm。

答：999 mm4. 边长为a的正方形截面梁，按图示两种不同形式放置，在相同弯矩作用下，两者最大正应力之比max amax b()()σσ=。

(a)(b)答：2/15. 一工字截面梁，截面尺寸如图，, 10h b b t ==。

试证明，此梁上,下翼缘承担的弯矩约为截面上总弯矩的88%。

证：412, (d ) 1 8203BA z z zMy M Mt M y yb y I I I σ==⨯=⨯⎰4690z I t=41411 82088%3690M t M t=⨯⨯≈ 其中：积分限1 , 22h h B t A M =+=为翼缘弯矩6. 直径20 mm d =的圆截面钢梁受力如图，已知弹性模量200 GPa E =, 200 mm a =，欲将其中段AB 弯成 m ρ=12的圆弧，试解：1MEIρ=而M Fa =4840.78510 m , 0.654 kN 64d EII F aπρ-==⨯==33max80.654100.22010167 MPa 2220.78510M d Fad I I σ--⋅⨯⨯⨯⨯====⨯⨯ 7. 钢筋横截面积为A ，密度为 ρ，放在刚性平面上，一端加力F ，提起钢筋离开地面长度3l解：截面C 曲率为零2(/3)0, 326C Fl gA l gAl M F ρρ=-==8. 矩形截面钢条长l ，总重为F ，放在刚性水平面上，在钢条A 端作用3F解：在截面C 处， 有 10C M EIρ==2()2 0, 323AC C AC AC l F F lM l l l =⨯-⨯==即AC段可视为受均布载荷q 作用的简支梁2maxmax 22()/8/63AC M q l FlWbt bt σ===9. 图示组合梁由正方形的铝管和正方形钢杆套成，在两端用刚性平板牢固联接。

4-1(4-1)试求图示各梁中指定截面上的剪力和弯矩。

解：（a）（b）（c）（d）=（e）（f）（g）（h）=返回4-2(4-2) 试写出下列各梁的剪力方程和弯矩方程，并作剪力图和弯矩图。

解：（a）（b）时时（c）时时（d）（e）时，时，（f）AB段：BC段：（g）AB段内：BC段内：（h）AB段内：BC段内：CD段内：返回4-3(4-3)试利用荷载集度、剪力和弯矩间的微分关系作下列各梁的剪力图和弯矩图。

返回4-4(4-4)试作下列具有中间铰的梁的剪力图和弯矩图。

返回4-5(4-6)已知简支梁的剪力图如图所示。

试作梁的弯矩图和荷载图。

已知梁上没有集中力偶作用。

返回4-6(4-7) 试根据图示简支梁的弯矩图作出梁的剪力图与荷载图。

返回4-7(4-15)试作图示刚架的剪力图、弯矩图和轴力图。

返回4-8(4-18)圆弧形曲杆受力如图所示。

已知曲杆轴线的半径为R，试写出任意横截面C上剪力、弯矩和轴力的表达式（表示成角的函数），并作曲杆的剪力图、弯矩图和轴力图。

解：（a）（b）返回4-9(4-19)图示吊车梁，吊车的每个轮子对梁的作用力都是F，试问：（1）吊车在什么位置时，梁内的弯矩最大？最大弯矩等于多少？（2）吊车在什么位置时，梁的支座反力最大？最大支反力和最大剪力各等于多少？解：梁的弯矩最大值发生在某一集中荷载作用处。

，得：当时，当M极大时：，则，故，故为梁内发生最大弯矩的截面故：=返回4-10(4-21)长度为250mm、截面尺寸为的薄钢尺，由于两端外力偶的作用而弯成中心角为的圆弧。

已知弹性模量。

试求钢尺横截面上的最大正应力。

解：由中性层的曲率公式及横截面上最大弯曲正应力公式得：由几何关系得：于是钢尺横截面上的最大正应力为：4-11(4-25) 矩形截面的悬臂梁受集中力和集中力偶作用，如图所示。

试求截面m-m和固定端截面n-n上A，B，C，D四点处的正应力。

解：对m-m及n-n截面，都给以坐标系如图所示。

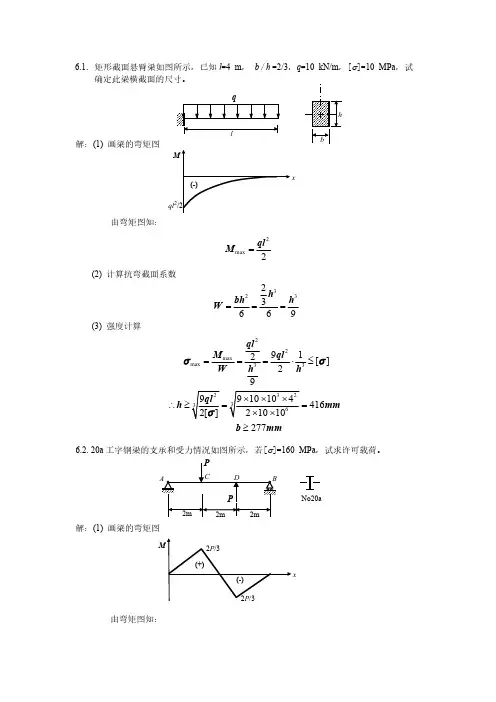
6.1.矩形截而悬臂梁如图所示，已知1=4 b/h=2!3, q二10 kN/m, [cr]=10 MPa,试确定此梁横截面的尺寸.max 2(2)计算抗弯截面系数2,3W 如31"yy = ----- = ------- =—6 6 9(3)强度计算0尸max W M 2 h3~[T/9X10X103X42心/. h > / —— = 3 ------------------- - - =416〃〃〃\2[(T] V 2xl0xl06b > 277mm62 20a工字钢梁的支承和受力情况如图所示，若[a]=160 MPa,试求许可载荷。

由弯矩图知:2P= = J_.pgEW W 3W.• A 哄=3x237xl0F60>d。

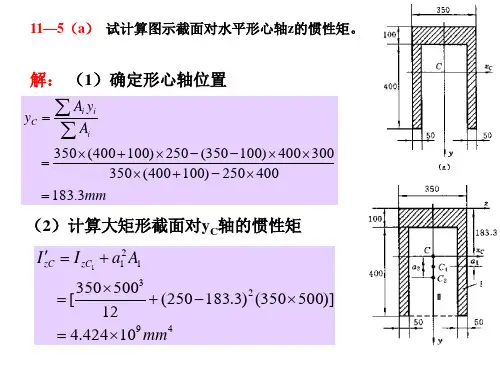
”= %.8 球2取许可载荷[P] = 57AN解：(1)画梁的弯矩图M c M c 32xl.34xl03=—=—Y = :— = 63.2MPaW c诚;. n x 0.06?"3TB截面:0.9xlO3 5z 4——；------------ -- = 62.1 MPa力以八d；、〃x0.06 〃 0.045、---- U ——r)------------ (1 —----- r-)32 矶32 0.064(3)轴内的最大正应力值(2)查表得抗弯截面系数(3)强度计算2P、=——W =237x10^7/1maxbfmax63.图示圆轴的外伸部分系空心轴.试作轴弯矩图，并求轴内最大正应力.由弯矩图知：可能危险截面是C和B截而(2)计算危险截而上的最大正应力值C截面：解：(1)画梁的弯矩图M t = 308M H(2)计算抗弯截面系数(3)强度计算 许用应力[(r] = ^- = — = 253MPa n 1.5强度校核308 inA1/rn r 】b” = —- = ------------------ I T = 1961"“ Y b maxW 1.568x1 Of压板强度足够。

弯曲应力习题答案在材料力学中，弯曲应力是结构分析中的一个重要概念，它涉及到梁或板在受到弯曲作用时内部产生的应力。

以下是一些弯曲应力习题的答案示例：习题一：简单梁的弯曲应力计算问题描述：一根长为 \( L \) 米，截面为矩形的梁，宽 \( b \) 米，高 \( h \) 米，材质为钢，弹性模量 \( E \) 为 \( 200 \) GPa。

梁的一端固定，另一端自由，中间受到一个集中力 \( P \) 的作用。

解答：1. 首先，确定梁的截面惯性矩 \( I \)：\[ I = \frac{b \cdot h^3}{12} \]2. 根据梁的受力情况，计算梁的弯曲应力 \( \sigma \)：\[ \sigma = \frac{M \cdot c}{I} \]其中 \( M \) 是弯矩，对于集中力 \( P \) 作用在梁的中点，弯矩 \( M \) 为 \( \frac{PL}{4} \)。

3. 将弯矩代入弯曲应力公式中：\[ \sigma = \frac{P \cdot L \cdot c}{4 \cdot I} \] 其中 \( c \) 是梁截面上距离中性轴的距离，对于矩形截面，\( c = \frac{h}{2} \)。

4. 将已知数值代入公式，计算出弯曲应力。

习题二：悬臂梁的弯曲应力分析问题描述：一根悬臂梁，长度 \( L \) 米，材料的弹性模量 \( E \) 为 \( 200 \) GPa，梁的一端固定，另一端受到一个向下的集中力 \( P \)。

解答：1. 悬臂梁在末端受到集中力作用时，最大弯矩 \( M \) 出现在梁的末端，其值为 \( P \cdot L \)。

2. 假设梁的截面为圆形，半径 \( r \)，则截面惯性矩 \( I \) 为： \[ I = \frac{\pi r^4}{4} \]3. 计算弯曲应力 \( \sigma \)：\[ \sigma = \frac{M}{I} = \frac{P \cdot L}{\frac{\pir^4}{4}} \]4. 将已知数值代入公式，计算出弯曲应力。

弯曲应力1.圆形截面简支梁A,B套成，A,B层间不计摩擦，材料的弹性模量E B=2E A求在外力偶矩M e作用下，A,B中最大正应力的比值^max有4个答案:Bmin1(A)-；61 (C)1；81(D)丄10答: B2.矩形截面纯弯梁，材料的抗拉弹性模量E t大于材料的抗压弹性模量E c，则正应力在截面上的分布图有以下4种答案：(A) (B) (C) (D) 答: C3.将厚度为2 mm的钢板尺与一曲面密实接触，已知测得钢尺点A处的应变为—，则该曲面在点A1000处的曲率半径为_________ m m。

答：999 mmP4.边长为a的正方形截面梁，按图示两种不同形式放置，在相同弯矩作用下，两者最大正应力之比匕丛= ___________(%x)bO(b)答：1/ , 25. 一工字截面梁，截面尺寸如图，h二b, b =10t。

试证明，此梁上，下翼缘承担的弯矩约为截面上总弯矩的88%证: — My M12MA y(ybdy) =1 820 罟3Iz4 l z=690tM1 Mt4 1勺8207 6904”88%I yh/2—- 丄h/2zt其中：积分限Bt? , A弓为翼缘弯矩6. 直径d =20 mm 的圆截面钢梁受力如图，已知弹性模量E = 200 GPa , a =200 mm ，欲将其中段AB 弯成 f m 的圆弧，试求所需载荷，并计算最大7. 钢筋横截面积为A ，密度为「，放在刚性平面上，一端加力F ，提起钢筋离 开地面长度-。

试问F 应多大?3解：截面C 曲率为零2Fl gA(l /3) 3 28. 矩形截面钢条长l ，总重为F ，放在刚性水平面上，在钢条A 端作用|向上的拉力时，试求钢条内最大正应力。

解：在截面C 处，有―罟丸弯曲正应力。

解：1 = M 而 M 二 Fa P EI Fmax64 =0.785 10 岀 m 4, 「旦 Pa = 0.654 kN21 Fad 21 3 3 0.654 1 03 0.2 20 10 2 0.785 10 出 = 167 MPa即M C =F Is3 l AC F (I AC )2 l 2 2l AC AC 段可视为受均布载荷q 作用的简支梁 max max 2q(U c ) /8 _ Fl bt 2/6 3bt 2iF/3 C9.图示组合梁由正方形的铝管和正方形钢杆套成，在两端用刚性平板牢固联接。

6.1. 矩形截面悬臂梁如图所示,已知l =4m , b /h =2/3,q =10kN/m ,[σ]=10MPa ,试肯定此梁横截面的尺寸. 解：(1) 画梁的弯矩图由弯矩图知：(2) 盘算抗弯截面系数32323669h bh h W ===(3) 强度盘算22maxmax 33912[]29416 277ql M ql h Wh h mm b mmσσ===⋅≤∴≥==≥6.2. 20a 工字钢梁的支承和受力情形如图所示,若[σ]=160MPa ,试求允许载荷.解：(1)画梁的弯矩图(2) 查表得抗弯截面系数6323710W m -=⨯(3) 强度盘算max max 66223[]33[]3237101601056.8822PM P W W WW P kNσσσ-===⋅≤⨯⨯⨯⨯∴≤==取允许载荷No20ax ql x[]57P kN =6.3. 图示圆轴的外伸部分系空心轴.试作轴弯矩图,并求轴内最大正应力.解：(1)(2) C 截面：3max3332 1.341063.20.0632C C C C C M M MPa d W σππ⨯⨯====⨯B 截面：3max3434440.91062.10.060.045(1)(1)32320.06B B B BB B B M M MPa D d W D σππ⨯====⨯--(3) 轴内的最大正应力值MPa C 2.63max max ==σσ6.5.把直径d =1m 的钢丝绕在直径为2m 的卷筒上,设E =200GPa,试盘算钢丝中产生的最大正应力. 解：(1) 由钢丝的曲率半径知1M E M EI I ρρ=∴=(2) 钢丝中产生的最大正应力93max200100.510100 1MR ER MPa I σρ-⨯⨯⨯====6.8. 压板的尺寸和载荷如图所示.材料为45钢,σs =380MPa ,取安全系数n=1.5.试校核压板的强度.x解：(1)(2) 232363330.030.0212(1)(1) 1.568106620bH hW m H -⨯=-=-=⨯(3) 强度盘算许用应力380[]2531.5SMPa nσσ===强度校核max 6308196[]1.56810A M MPa W σσ-===⨯压板强度足够.6.12.图示横截面为⊥形的铸铁推却纯曲折,材料的拉伸和紧缩许用应力之比为[σt ]/[σc ]=1/4.求程度翼缘的合理宽度b .解：(1) ,max 11320 c c y mm=(2) 由截面形心地位()()304006017060370320304006060510 i CiC iA y b y Ab b mm⨯-⨯+⨯⨯===⨯-+⨯=∑∑6.13. ⊥形截面铸铁梁如图所示.若铸铁的许用拉应力为[σt ]=40MPa ,许用压应力为[σc ]=4P . 解：(1)(2) A ()22max 86320.8[][]101801016010132.60.80.825096.410A C C zC zCzC C M h Ph I I I P kN h σσσ--==≤⨯⨯⨯∴≤==-⨯A 截面的最大拉应力11max 86310.8[][]1018010401052.80.80.896.410A t t zC zCzC t M h Ph I I I P kNh σσσ--==≤⨯⨯⨯∴≤==⨯⨯C 截面的最大拉应力()22max 86320.6[][]1018010401044.20.60.625096.410C t t zC zCzC t M h Ph I I I P kN h σσσ--==≤⨯⨯⨯∴≤==-⨯取许用载荷值[]44.2P kN =6.14. 铸铁梁的载荷及截面尺寸如图所示.许用拉应力[σl ]=40MPa ,许用压应力[σc ]=160MPa .解：(1) 画梁的弯矩图(2) 盘算截面几何性质42.572.522264157.542.53020021520030100157.5 30200200303020060.12510i CiC i zCAA y y mmAIy dA y dy y dy m --⨯⨯+⨯⨯===⨯+⨯==⨯⨯+⨯⨯=⨯∑∑⎰⎰⎰(3) 强度盘算B 截面的最大压应力3max620100.157552.4 []60.12510B C C C zC M y MPa I σσ-⨯⨯===⨯B 截面的最大拉应力3max6(0.23)2010(0.230.1575)24.12 []60.12510B C t t zC M y MPa I σσ--⨯-===⨯C 截面的最大拉应力3max610100.157526.2 []60.12510C C t t zC M y MPa I σσ-⨯⨯===⨯梁的强度足够.(4) 评论辩论：当梁的截面倒置时,梁内的最大拉应力产生在B 截面上.3max620100.157552.4 []60.12510B C t t ZC M y MPa I σσ-⨯⨯===⨯梁的强度不够.6.19. 试盘算图示工字形截面梁内的最大正应力和最大剪应力. xmax max 15 20 Q kN M kNm==(2) 查表得截面几何性质3*max14113.8 6z z I W cm cm b mmS ===(3) 盘算应力最大剪应力*3max max max151018.10.0060.138Z Z Q S MPabI τ⨯===⨯最大正应力3max max62010141.814110M MPa W σ-⨯===⨯6.22. 起重机下的梁由两根工字钢构成,起重机自重Q=50kN ,起重量P=10kN .许用应力[σ]=160MPa ,[τ]=100MPa .若暂不斟酌梁的自重,试按正应力强度前提选定工字钢型号,然后再按剪应力强度前提进行校核.解：(1)(2) (3) C 截面：B()(506)()501204.17C C M x x x dM x x dxx m =-=-==此时C 和D 截面的弯矩是104.25 134.05C D M kNm M kNm==D 截面：()(106)(8)()381203.17D D M x x x dM x x dxx m =+-=-==此时C 和D 截面的弯矩是98.27 140.07C D M kNm M kNm==最大弯矩值是max 140.07 M kNm=(4) 按最大正应力强度前提设计查表取25b *max1021.3z z I b mm cmS==(5) 按剪应力强度校核当起重机行进到最右边时（x =8m ）,梁内剪应力最大; x剪应力强度盘算*3max maxmax581013.6[]220.010.213zzQ SMPabIττ⨯===⨯⨯剪应力强度足够.6.23. 由三根木条胶合而成的悬臂梁截面尺寸如图所示,跨度l=1 m.若胶合面上的许用切应力为0.34 MPa,木材的许用曲折正应力为[σ[τ]=1 MPa,试求允许载荷P解：(1)max maxQ P M Pl==(2) 梁曲折正应力强度前提maxmax2262[]16[]10100.10.153.75661M PlW bhbhP kNlσσσ==≤⨯⨯⨯≤==⨯(3) 梁曲折切应力强度前提maxmax633[]222[]21100.10.151033Q PA bhbhP kNτττ==≤⨯⨯⨯⨯≤==(4)胶合面上切应力强度前提2222max1336312222[]244212[]0.34100.10.153.8250.15660.02544zQ h P hy ybhIbhP kNhyτττ⎛⎫⎛⎫=-=-≤⎪ ⎪⎝⎭⎝⎭⨯⨯⨯⨯≤==⎛⎫⎛⎫--⎪ ⎪⎝⎭⎝⎭允许载荷：[P]=3.75 kN.6.27.在图中,梁的总长度为l ,受均布载荷q 感化.若支座可对称地向中点移动,试问移动距离为若干时,最为合理？ 解：(1) 束缚反力2B C ql R R ==(2) 截面上的最大正弯矩和最大负弯矩22,max 2,max228822ql l ql ql qla M a qa M +-⎛⎫=--=- ⎪⎝⎭=-(3) 二者数值相等时最为合理2222822440410.20782ql qla qa a la l l a l l-=+-=-+-+===。

弯 曲 应 力基 本 概 念 题一、择题(如果题目有5个备选答案，选出2～5个正确答案，有4个备选答案选出一个正确答案。

)1. 弯曲正应力的计算公式y I Mz=σ的适用条件是（ ）。

A . 粱材料是均匀连续、各向同性的 B ．粱内最大应力不超过材料的比例极限 C ．粱必须是纯弯曲变形 D ．粱的变形是平面弯曲 E ．中性轴必须是截面的对称轴 2. 在梁的正应力公式y I Mz=σ中，I z 为粱的横截面对（ ）轴的惯性矩。

A . 形心轴 B ．对称轴 C ．中性轴 D ．形心主惯性轴 3. 梁的截面为空心圆截面，如图所示，则梁的抗弯截面模量W 为（ ）。

A .323D π B ．)1(3243απ-D C ．323d πD ．323233d D ππ-E ．2646444Dd D ππ-题3图 题4图4. 欲求图示工字形截面梁上A 点剪应力τ，那么在剪应力公式zzS bI S F *=τ中，S *z 表示的是（ ）对中性轴的静矩。

A ．面积IB ．面积ⅡC ．面积I 和ⅡD ．面积Ⅱ和ⅢE ．整个截面面积-21-5．欲求题4图所示工字形截面梁上A 点剪应力τ，那么在剪应力公式zzS bI S F *=τ中，b应取（ ）。

A ．上翼缘宽度B ．下翼缘宽度C ．腹板宽度D ．上翼缘和腹板宽度的平均值 6．图为梁的横截面形状。

那么，梁的抗弯截面模量W z ＝（ ）。

A . 62bh B ．32632d bh π-C ．2641243hd bh ⎪⎪⎭⎫⎝⎛-π D ．⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛-22641243d h d bh π7．两根矩形截面的木梁叠合在一起(拼接面上无粘胶无摩擦)，如图所示。

那么该组合梁的抗弯截面模量W 为( )A . 62bhB ．⎪⎪⎭⎫ ⎝⎛622bh C ．)2(612h b D ．h bh 21222⎪⎪⎭⎫⎝⎛8．T 形截面的简支梁受集中力作用(如图)，若材料的[σ]- ＞[σ]+，则梁截面位置的合理放置为( )。