高频电子线路 非线性电路基本分析方法
- 格式:ppt
- 大小:420.50 KB
- 文档页数:23


1.4 非线性电路的分析方法如前所述,在小信号放大器的分析和设计中, 通常是采用等效电路法,以便采用经典电路理论来进行分析、计算。
线性电路中,通常信号幅度小,整个信号的动态范围在元器件特性的线性范围内,所以器件的参数均视为常量,可以借助于公式计算电路的性能指标。
“模拟电子技术基础”课程中“低频小信号放大器”以及本课程中 “高频小信号谐振放大器”的分析中都涉及线性电路的分析。
在通信电子线路中,除了小信号放大电路外,有源器件还常工作在大信号或非线性状态。
与线性电路相比,非线性电路的分析和计算要复杂得多。
在非线性电路中,信号的幅度较大时,信号的动态范围涉及元器件特性的整个范围,半导体器件工作在非线性状态。
它们的参数不再是常数而是变量了。
因此,难以用等效电路和简单的公式计算电路了。
此外,在线性、非线性频谱搬移电路中,都涉及非线性电路的分析方法。
非线性电路的分析是本课程中的重要内容。
分析非线性电路时,常用幂级数分析法、指数函数分析法、折线分析法、开关函数分析法和时变参数分析法等。
1.4.1 幂级数分析法常用的非线性元器件的特性曲线大都可以用幂级数来表示。
在小信号运用的条件下,可以将一些非线性元器件的特性曲线用幂级数近似表示,使问题简化。
用这种方法分析非线性电路,虽然存在一定的准确性问题,但可以较好地说明非线性器件的频率变换作用。
因此在小信号检波、小信号调幅等电路分析时常常采用。
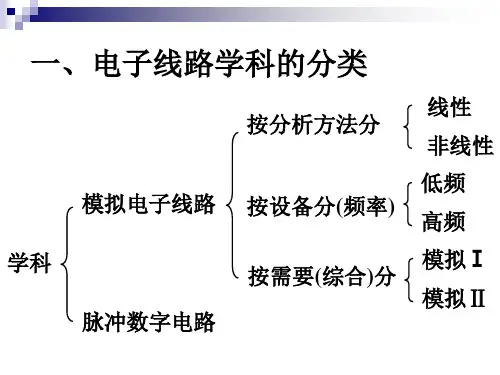
下面以图1.4.1所示电路为例,介绍幂级数分析法。
图中二极管是非线性器件,所加信号电压u 的幅度较小,称为小信号;L R 为负载, 0U 是静态工作点电压。
设流过二极管的电流i 函数关系为:)(u f i =若该函数)(u f 的各阶导数存在,则这个函数可以在静态工作点0U 处展开成幂级数(或称为泰勒级数)。
+-+-+-+=300///200//00/0)(!3)()(!2)())(()(U u U fU u U fU u U f U f i+-+-+-+=303202010)()()(U u b U u b U u b b (1-4-1)式中 0)(00U u iU f b ===为工作点处的电流u LR 图 1.4.1 二极管及其伏安特性(a)o(b)Id d )(0/1U u ui U f b === 为过静态工作点切线的斜率,即跨导;0220//2d d !21)(U u ui U f b ===kk0k k d d !1)(U u ui K U f b ===如果取00=U ,即静态工作点选在原点,则式(1-4-1)可写为 ++++=332210u b u b u b b i (1-4-2)从数学分析来看,上述幂级数展开式是一收敛函数,幂次越高的项其系数越小。

非线性电路分析技巧在电子领域中,非线性电路的分析是十分重要的。
与线性电路不同,非线性电路的元件特性与电压和电流之间的关系不是线性的。
因此,针对非线性电路的分析方法需要更为复杂和精确。
本文将介绍一些非线性电路分析的技巧,帮助读者更好地理解和应用于实践。
一、利用近似法分析非线性电路中,非线性元件的特性曲线通常很复杂,很难直接得到解析解。
此时,我们可以利用近似法来简化问题,使其更易于分析。
最常用的近似方法之一是泰勒级数展开。
通过将非线性特性曲线在某个工作点处展开,可以得到一个线性近似,进而使用线性分析方法进行求解。
其他常用的近似方法还包括小信号模型和大信号模型等。
二、使用等效电路模型为了更方便地分析非线性电路,我们可以将其等效为线性电路。
这样,我们就可以使用线性电路的分析方法进行求解。
等效电路模型可以通过查找手册、仿真软件或实验数据来获取。
常见的等效电路模型包括二极管的小信号模型、伏安特性曲线拟合模型等。
通过将非线性元件替换为等效线性元件,可以将问题简化并应用线性电路分析法。
三、使用迭代法对于复杂的非线性电路,我们可以使用迭代法逐步逼近真实解。
迭代法通常结合着近似法和等效电路模型。
步骤如下:首先,根据近似法建立初始的线性近似电路;然后,通过求解线性近似电路得到数值解;接着,将数值解代入非线性元件中得到新的特性曲线;最后,根据新的特性曲线更新线性近似电路,并重复上述步骤直到收敛为止。
四、考虑非线性电路的稳定性非线性电路的稳定性问题是在分析时需要特别关注的。
由于非线性电路的元件特性会随着电压和电流变化,系统可能会失去稳定性。
为了确保电路正常工作,我们需要对非线性电路进行稳定性分析。
常见的稳定性判断方法包括利用极点分布法、利用Bode图分析法和利用Lyapunov稳定性判据等。
五、利用仿真软件进行分析随着计算机技术的不断发展,仿真软件已经成为非线性电路分析的重要工具。
利用仿真软件,我们可以建立电路的数学模型,并模拟其电压、电流和功率等参数的变化。



非线性电路分析方法摘要:我要将电路元件的范围及其相应的分析方法进行拓展,引入对非线性二端元件的分析和总结。
非线性二端元件就是接线端自变量和接线端的函数具有非线性关系的元件。
下面对非线性电路的分析方法进行分类和总结:关键词:非线性电路 直接分析法 数值分析法 图形分析法 分段线性分析法 小信号分析法0.引言到目前为止,我们已经学习过若干种线性元件的电路,也学习过这些元件构成的线性电路分析法。
本文将就非线性问题进行分类和归纳总结。
1.直接分析法此方法一般应用于对非线性二端元件的函数关系较简单时使用,结合并运用线性元件电路的分析方法和一些定理,同时列写出非线性的补充方程,最后通过求解数学问题并结合电路实际解答的方法。
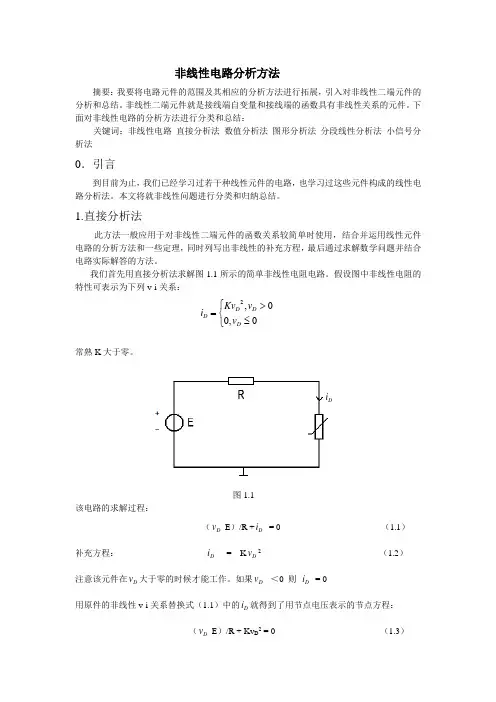
我们首先用直接分析法求解图1.1所示的简单非线性电阻电路。
假设图中非线性电阻的特性可表示为下列v-i 关系:2,00,0D D D DKv v i v ⎧>=⎨≤⎩常熟K 大于零。
D i图1.1该电路的求解过程:(D v -E )/R +D i = 0 (1.1) 补充方程: D i = K D v 2 (1.2) 注意该元件在D v 大于零的时候才能工作。
如果D v <0 则 D i = 0用原件的非线性v-i 关系替换式(1.1)中的D i 就得到了用节点电压表示的节点方程: (D v -E )/R + Kv D 2 = 0 (1.3)化简式(1.3),得到下列二次方程:RK D v 2 + D v – E = 0 求出D v 并选择正解,即:12D v RK-+=(1.4)对应的i D 表达式可通过将上式替换式(1.2)得到,即:D i= 12K RK ⎛- ⎝⎭小结:这类分析方法很有局限性,通常只适用于函数关系较简单的非线性求解问题,对于较复杂的问题,下面我将讨论到。
2.数值分析法当所求非线性的函数关系不是简单的函数关系时,已经不能用已有的公式去求解,这是就需要在误差精度允许的范围内,运用计算方法学的知识寻求所需的解,下面介绍常用到的计算方法:《电路基理论础》中给出的3种方法: ① 前向欧拉法(Forward Euler method ):(以后本论文均以(,)dy f y x dx =表示dy dx) 1k y + = k y + h f (k y , k x )其中h 为积分步长② 后向欧拉法 (Backward Euler method )1k y + = k y + h f ( 1k y + , 1k x + )③ 梯形法(trapezoidal method )1k y += k y + 0.5[f (k y , k x ) + f ( 1k y + , 1k x +) ] 也就是我们所熟悉的梯形公式 还有几种常用的计算方法:④ 辛普森公式(Simpson )也作抛物线公式: 1k y += k y +16{f ( k y , k x )+ 4f [0.5(k y + y k+1) ,0.5(k x + 1k x +)] +f (1k y + , 1k x + )} ⑤ 牛顿(Newton )法 (也作切线迭代法):该公式多用于复杂的函数的求根运算,设()y f x =1n x += n x -()()n n f x f x '⑥ 拉格朗日差值n 次型对于无法求出具体表达式的非线性函数,在已知图像上若干点的情况时,可以用n 次多项式进行近似的拟合,我所学过的有牛顿型差值公式和拉格朗日型差值,下面只介绍拉格朗日型差值公式,牛顿型差值比较类似。

