实训任务2.3等效变换法分析复杂电路3..

学习情境二电桥电路的设计与测试第一部分思考题2.1 什么叫做电压源和电流源？二者之间的等效变换条件什么？二者在方向上有何联系？2.2 什么叫理想电压源和理想电流源？为什么它们之间不能进行等效变换？2.3 叙述支路电流法的解题步骤。

2.4 节点电压法适用于计算什么电路？如何列节点电压方程？试述节点电压法解题步骤。

2.5 什么是叠加定理？请叙述应用叠加定理求电路中各支路电流的步骤。

2.6 简述戴维南定理的内容，说明使用条件用来分析电路的基本步骤。

2.7 “一线性有源二端电路的戴维南等效源的内阻为，则上消耗的功率就是有源二端电路中所有电阻及电源所吸收的功率之和。

”？这种观点对吗？为什么？2．8若电路两端既不允许短路也不允许断路，如何用实验方法确定其戴维南等效电路？2．9设计两种测量输入电阻的方法，写出原理和步骤，可做实际练习。

第二部分精选习题2.1 如图所示，试求电源发出的功率。

2.2 试求图示电路的等效电压源。

2.3 已知，Ω，试运用电源的等效变换法求图示中的电流。

2.4 用电源等效变换法求图示电路中的电流I。

2.5 用回路电流法求图示电路中的电压U。

2.6 用回路电流法求图示电路中受控源的功率。

2.7 用节点电位法求图示电路中各支路的电流。

2.8 用节点电位法求图示电路中电压源支路的电流I。

2.9 如图所示为一种模拟计算机的加法电路。

图中、、为被加电源电压，试用节点电压法证明：⑴当时，⑵当＜＜2.10 利用节点电压法求图示各支路电流。

2.11 如图所示，试用叠加定理求通过恒压源的电流（写过程、列式）。

2.12 用叠加定理计算图示电路中电压的数值。

如果右侧电源反向，电压变化多大？2.13用叠加定理求图示电路中的U。

2.14 测得一个有源二端网络的开路电压为60伏，短路电流为3安，如把=100欧的电阻接支网络的引出端点，试问上的电压是多大？2.15 有一个有源二端网络，用内阻为50 千欧的电压表测得它两端的电压为30伏，用内阻为100 千欧的电压表测得它两端的电压为50伏，试求这个网络的等效电压源。

一、实训目的通过本次实训，使学生掌握电源等效代换的基本原理和方法，提高学生对电路分析的实际操作能力，加深对电路理论知识的理解。

二、实训内容1. 实训器材：直流稳压电源、电阻、电流表、电压表、电路板、导线等。

2. 实训步骤：（1）搭建电路：按照实训要求，搭建一个含有电阻的电路，并连接直流稳压电源。

（2）测量电压：使用电压表测量电源输出端的电压，记录数据。

（3）测量电流：使用电流表测量电路中的电流，记录数据。

（4）计算电源等效电压：根据实际电压源等效为实际电流源的方法，计算电源等效电压。

（5）计算等效电流源：根据实际电流源等效为实际电流源的方法，计算等效电流源。

（6）验证等效电路：将计算出的等效电压源或等效电流源代入原电路，观察电路中电流、电压的变化情况，验证等效电路的正确性。

三、实训原理1. 实际电压源等效为实际电流源：实际电压源等效为实际电流源时，电流方向和之前的一致，大小为之前电压除上在电源支路上的电阻。

2. 实际电流源等效为实际电流源：确定电流源的方向，知道这个的方向之后，根据电流从正级流向负级的原则，只要在等效的电压源支路上标好和之前的电路方向一致，则出来的这端就是正，另一边就是负。

四、实训结果与分析1. 搭建电路：按照实训要求，成功搭建了含有电阻的电路，并连接直流稳压电源。

2. 测量电压：电源输出端的电压为5V。

3. 测量电流：电路中的电流为0.5A。

4. 计算电源等效电压：根据实际电压源等效为实际电流源的方法，计算电源等效电压为5V/1Ω=5A。

5. 计算等效电流源：根据实际电流源等效为实际电流源的方法，确定电流源的方向，然后计算等效电流源为5A。

6. 验证等效电路：将计算出的等效电压源代入原电路，观察到电路中电流、电压的变化情况与原电路一致，验证等效电路的正确性。

五、实训总结1. 通过本次实训，掌握了电源等效代换的基本原理和方法，提高了电路分析的实际操作能力。

2. 在实训过程中，注意了电路搭建、测量数据、计算结果等细节，确保了实训的顺利进行。

一、实验目的1. 理解并掌握等效变换的基本概念和原理。

2. 通过实际操作，验证电压源与电流源等效变换的条件。

3. 学会使用实验仪器进行电源外特性的测试。

4. 增强对电路分析方法的理解和应用能力。

二、实验原理等效变换是指在电路分析中，将复杂的电路简化为等效的简单电路，使得简化后的电路与原电路在某些方面具有相同的电性能。

常见的等效变换包括电压源与内阻的等效电压源、电流源与内阻的等效电流源等。

电压源与电流源的等效变换条件如下：- 电压源（Us）与内阻（Rs）串联可以等效为一个电流源（Is）与内阻（Rs）并联。

- 电流源（Is）与内阻（Rs）并联可以等效为一个电压源（Us）与内阻（Rs）串联。

等效变换的公式为：- 对于电压源与内阻的等效变换：Is = Us / Rs- 对于电流源与内阻的等效变换：Us = Is Rs三、实验器材1. 直流稳压电源1台2. 直流恒流源1台3. 直流数字电压表1块4. 直流数字电流表1块5. 可调电阻箱1个6. 电阻器若干7. 电线若干四、实验步骤1. 按照实验电路图连接电路，将直流稳压电源或直流恒流源作为电源接入电路。

2. 使用电压表和电流表测量电路中各个元件的电压和电流值。

3. 根据测得的电压和电流值，计算电路的等效电压源或等效电流源。

4. 将计算得到的等效电压源或等效电流源接入电路，再次测量电路中各个元件的电压和电流值。

5. 比较两次测量结果，验证等效变换的正确性。

五、实验数据及结果分析1. 实验一：电压源与内阻的等效变换- 实验电路：将直流稳压电源接入电路，测量电路中各个元件的电压和电流值。

- 等效变换：根据测得的电压和电流值，计算等效电流源。

- 实验结果：将计算得到的等效电流源接入电路，测量电路中各个元件的电压和电流值，与原电路结果基本一致。

2. 实验二：电流源与内阻的等效变换- 实验电路：将直流恒流源接入电路，测量电路中各个元件的电压和电流值。

- 等效变换：根据测得的电压和电流值，计算等效电压源。

2.3 电路的等效变换1. 电路等效变换的由来对于一个电路来说，有时我们关注的是电路中所有的细节。

但在大多数情况下，我们主要关注的其实只是电路中某一部分的细节。

那么我们不太关注的部分怎么办？我们很自然想到的办法就是将不太关注的部分尽可能简化，从而将注意力尽可能集中到我们最想关注的部分。

这就是我们引入等效变换这一方法的初衷。

等效变换就是将电路中不太关注部分进行简化的一种方法。

当然了，这种简化不是随随便便地简化，而是必须满足一定的条件。

这就是接下来我们要讲的等效变换的定义。

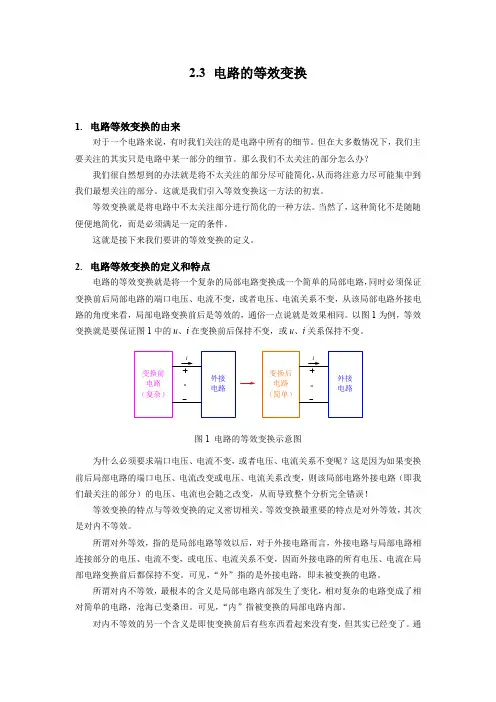
2. 电路等效变换的定义和特点电路的等效变换就是将一个复杂的局部电路变换成一个简单的局部电路，同时必须保证变换前后局部电路的端口电压、电流不变，或者电压、电流关系不变，从该局部电路外接电路的角度来看，局部电路变换前后是等效的，通俗一点说就是效果相同。

以图1为例，等效变换就是要保证图1中的u 、i 在变换前后保持不变，或u 、i 关系保持不变。

图1 电路的等效变换示意图为什么必须要求端口电压、电流不变，或者电压、电流关系不变呢？这是因为如果变换前后局部电路的端口电压、电流改变或电压、电流关系改变，则该局部电路外接电路（即我们最关注的部分）的电压、电流也会随之改变，从而导致整个分析完全错误！等效变换的特点与等效变换的定义密切相关。

等效变换最重要的特点是对外等效，其次是对内不等效。

所谓对外等效，指的是局部电路等效以后，对于外接电路而言，外接电路与局部电路相连接部分的电压、电流不变，或电压、电流关系不变，因而外接电路的所有电压、电流在局部电路变换前后都保持不变。

可见，“外”指的是外接电路，即未被变换的电路。

所谓对内不等效，最根本的含义是局部电路内部发生了变化，相对复杂的电路变成了相对简单的电路，沧海已变桑田。

可见，“内”指被变换的局部电路内部。

对内不等效的另一个含义是即使变换前后有些东西看起来没有变，但其实已经变了。

通俗一点说，你还是你，但你已不是原来的你。

复杂直流电路的分析方法及灵活运用【摘要】复杂电路的分析在《电工基础》课程中占有比较重要的作用。

比较各种分析方法，熟练掌握，灵活运用。

【关键词】复杂电路；分析方法；灵活运用复杂直流电路的分析，在直流电路的求解中很重要。

分析复杂直流电路的方法很多，如支路电流法、回路电流法、叠加原理法等，有的方法普遍试用，但有时比较繁琐，根据电路的特点选择相应的方法来分析电路，比较方便。

在教学中，发现学生学习较死板，用法不灵活。

要求学生先观察电路的特点，掌握各种方法灵活运用。

一、复杂电路的概念及基本定理1.简单电路：能够转化成简单的串、并联的电路，称为简单电路。

也就是说，只要运用欧姆定律和电阻串、并联电路特点的计算公式，就能对它们进行分析和计算。

2.复杂电路：运用欧姆定律和电阻串并联特点及公式不能简化分析，这类电路，称为复杂电路。

如图1就是复杂电路。

图1 复杂直流电路图2节点3.基尔霍夫定律：分析复杂电路的方法很多，但都是基于两个基本定律——欧姆定律和基尔霍夫定律。

欧姆定律我们很熟悉，基尔霍夫定律，我们简单做一回顾：（1）基尔霍夫第一定律（节点定律）：流任一节点的电流之和恒等于流出该节点的电流之和，表达式为。

或者说流过任一节点的电流的代数和为零，表达式为∑I=0。

基尔霍夫第一定律表明电流具有连续性。

在电流的任一节点上，不可能发生电荷的积累。

即流入节点的总电量恒等于同一时间内从该节点流出的总电量。

如图2，对于节点A列出的节点方程为或（图2）在讲授节点定律时，用类比的方法，举例水流与电流，大河与分支小支流的流量的关系来方便学生的理解。

运用节点定律解题时，可列出任一节点的电流方程。

在列节点电流方程前，首先要标定电流方向，其原则是：对已知电流，按实际方向标出；对未知电流的方向，可任意标定。

最后根据计算结果来确定未知电流的方向。

计算结果为正，未知电流的实际方向与标定方向一致；计算结果为负，未知电流的实际方向与标定方向相反。

（2）基尔霍夫第二定律：也称为回路电压定律。

复杂电阻网络的处理方法在物理竞赛过程中经常遇到，无法直接用串联和并联电路的规律求出整个电路电阻的情况，这样的电路也就是我们说的复杂电路，复杂电路一般分为有限网络和无限网络。

那么，处理这种复杂电路用什么方法呢？下面，我就结合自己辅导竞赛的经验谈谈复杂电路的处理方法。

一：有限电阻网络原则上讲解决复杂电路的一般方法，使用基尔霍夫方程组即可。

它包含的两类方程出自于两个自然的结论：（1）对电路中任何一个节点，流出的电流之和等于流入的电流之和。

电路中任何一个闭合回路，都符合闭合电欧姆定律。

下面我介绍几种常用的其它的方法。

1：对称性简化所谓的对称性简化，就是利用网络结构中可能存在的对称性简化等效电阻的计算。

它的效果是使计算得以简化，计算最后结果必须根据电阻的串、并联公式；电流分布法；极限法等来完成。

在一个复杂的电路中，如果能找到一些完全对称的点，那么当在这个电路两端加上电压时，这些点的电势一定是相等的，即使用导线把这些点连接起来也不会有电流（或把连接这些点的导线去掉也不会对电路构成影响），充分的利用这一点我们就可以使电路大为简化。

例（1）如图1所示的四面体框架由电阻都为R的6根电阻丝连接而成，求两顶点A、B间的等效电阻。

图1图2分析:假设在A、B两点之间加上电压，并且电流从A电流入、B点流处。

因为对称性，图中CD两点等电势，或者说C、D 间的电压为零。

因此，CD间的电阻实际上不起作用，可以拆去。

原网络简化成简单的串、并联网络，使问题迎刃而解。

解：根据以上分析原网络简化成如图2所示的简单的串、并联网络，由串、并联规律得R AB=R/2例（2）三个相同的金属圈两两正交地连成如图所示的形状，若每一个金属圈的原长电阻为R，试求图中A、B两点之间的等效电阻。

图3 图4 图5分析：从图3中可以看出，整个电阻网络相对于AB的电流流入、流出方式上具有上下对称性，因此可上下压缩成如图所时的等效减化网络。

从如图4所示的网络中可以看出，从A点流到O电流与从O点到B电流必相同；从A1点流到O电流与从O点到B1电流必相同。

等效变换实验报告等效变换实验报告摘要：等效变换是电路分析中的重要概念，通过等效变换可以将复杂的电路简化为更易于分析的形式。

本实验旨在通过实际操作，验证等效变换的原理和应用。

实验中我们选取了一个具有多个电阻和电压源的电路，并通过等效变换将其简化为更为简单的形式。

实验结果表明，等效变换是一种有效的电路简化方法。

引言：在电路分析中，我们经常会遇到复杂的电路，由于其结构复杂，分析起来往往困难重重。

为了更好地理解电路的行为和性质，我们需要将复杂的电路简化为更易于分析的形式。

等效变换就是一种常用的电路简化方法，通过等效变换，我们可以将原电路转化为具有相同电压和电流特性的简化电路，从而更方便地进行分析。

实验步骤：1. 选取一个具有多个电阻和电压源的电路作为实验对象。

2. 根据等效变换的原理，通过适当的变换将原电路简化为等效电路。

3. 测量原电路和等效电路的电压和电流，并进行比较分析。

4. 根据实验结果，验证等效变换的有效性。

实验结果与分析：在实验中，我们选取了一个包含多个电阻和电压源的电路。

首先，我们根据等效变换的原理，将该电路简化为等效电路。

通过适当的变换，我们成功地将原电路转化为了一个简单的等效电路，其中只包含一个电阻和一个电压源。

接下来，我们测量了原电路和等效电路的电压和电流，并进行了比较分析。

实验结果表明，在相同的输入条件下，原电路和等效电路的电压和电流几乎完全一致。

这说明通过等效变换，我们成功地将原电路简化为了一个具有相同电压和电流特性的等效电路。

这样一来，我们可以更方便地进行电路分析和计算。

结论：本实验通过实际操作验证了等效变换的原理和应用。

实验结果表明，等效变换是一种有效的电路简化方法，通过等效变换，我们可以将复杂的电路转化为更为简单的形式，从而更方便地进行分析和计算。

进一步讨论：等效变换在电路分析和设计中具有广泛的应用。

通过等效变换，我们可以将复杂的电路转化为简化的形式，从而更好地理解电路的行为和性质。