人教A版数学必修一河南省示范性高中罗山高中高三复习单元过关
- 格式:docx
- 大小:176.33 KB
- 文档页数:5

河南省示范性高中罗山高中2023届高三数学复习单元过关练:必修五 解三角形(理科 含解析)1.已知a 、b 、c 是△ABC 中A 、B 、C的对边,且1,5,a b c ===,则△ABC 的面积S =( ) A 、32B 、2C 、3D 、42.如果等腰三角形的顶角的余弦值为35,则底边上的高与底边的比值为( ) A .12 B .45 C .23D .1 3.在△ABC 中,内角,,A B C 的对边分别是,,a b c,若22a b -=,sin C B =,则A =( ) A . B . C . D . 4.在ABC ∆中,a =,b =,1cos 3C =,则ABC ∆的面积为( ). A...5.在△ABC 中,已知5cos 13A =,3sin 5B =,则cosC 的值为( ) A 、1665 B 、5665 C 、1665或5665D 、1665-6.若满足条件C=3π,AB=,BC=的三角形有两个,则的取值范围是 ( ) ()2,1..A ()3,2.B C.()2,37.ABC ∆的三个内角,,A B C 所对的边分别为,,a b c ,1sin cos sin cos ,2a B C c B Ab +=,a b B >∠=且则( ) A.6πB .3πC .23πD .56π8.A 为△ABC 的内角,则A A cos sin +的取值范围是( ) A .)2,2( B .)2,2(- C .]2,1(- D .]2,2[- 9.在ABC ∆中,045,60,1B C c ===,则最短边的边长等于 ( )A.12B.C.D.10.甲船在A 处观察到乙船在它的北偏东060的方向,两船相距a 海里,乙船正在向北行驶,若甲船的速度是乙船的3倍,甲船为了尽快追上乙船,应取北偏东θ方向前进,则=θ( ) A. 015 B. 030 C. 045 D. 06011.某人在C 点测得某塔在南偏西80°,塔顶仰角为45°,此人沿南偏东40°方向前进10米到D,测得塔顶A 的仰角为30°,则塔高为( ) (A)15米 (B)5米 (C)10米 (D)12米12.△ABC 中,根据下列条件,确定△ABC 有两解的是( )=18,b=20,A=120° =60,c=48,B=60° =3,b=6,A=30° =14,b=16,A=45° 13.在ABC ∆中,已知 45,1,2===B c b ,则C = . 14.满足6,2,45==︒=c a A 的ABC ∆的个数为 .15.在ABC ∆中,已知︒===60,1,3A c b ,则a = .16.两座相距60 m 的建筑物AB 、CD 的高度分别为20 m 、50 m ,BD 为水平面,则从建筑物AB 的顶端A 看建筑物CD 的张角为________.17.(三角形ABC 中,3,7==AB BC ,且53sin sin =B C . (1)求AC ; (2)求A ∠.18.在△ABC 中,设A 、B 、C 的对边分别为a 、b 、c ,向量m=(cosA,sinA),n=(-sinA,cosA),若|m+n|=2. (1)求角A 的大小;(2)若b=4,且c=a ,求△ABC 的面积. 19.((本题满分14分)在锐角ABC ∆中,,,a b c 分别是角,,A B C 2sin ,c A = (1)确定角C 的大小;(2)若c =ABC ∆面积的最大值.20.在ABC ∆中,已知内角3A π=,边BC =.设内角B x =,面积为y .(1)若4x π=,求边AC 的长;(2)求y 的最大值.21.在△ABC 中,a 、b 、c 分别为内角A B C 、、的对边,且()2sin (2)sin 2sin a A b c B c b C =+++.(1)求A 的大小;(5分)(2)若sin sin 1B C +=,判断△ABC 的形状.(7分)22.(本小题满分12分)如图,山脚下有一小塔AB,在塔底B测得山顶C的仰角为60°,在山顶C测得塔顶A 的俯角为45°,已知塔高AB=20 m,求山高CD.参考答案1.B 【解析】试题分析:由2223cos 25a b c C ab +-==,故4sin 5C =,故1sin 22S ab C ==。

河南省示范性高中罗山高中2020届高三数学复习单元过关练:选修2-3(含解析)1.某工厂某产品产量x (千件)与单位成本y (元)满足回归直线方程x y 82.136.77^-=,则以下说法中正确的是 ( )A .产量每增加1000件,单位成本下降1.82元B .产量每减少1000件,单位成本上升1.82元C .产量每增加1000件,单位成本上升1.82元D .产量每减少1000件,单位成本下降1.82元2.在代数式(4x 2-2x -5)(1+21x )5的展开式中,常数项为( )A.13B.14C.15D.163.设nxx )15(-的展开式的各项系数之和为M ,二项式系数之和为N ,若M -N=56,则展开式中常数项为 ( ) A .-15 B .1 5 C .10 D .-10 4.正态总体的概率密度函数为2()8()x x f x -∈=R ,则总体的平均数μ和标准差σ分别为( )A、0,8 B 、0,4C、0,2 D、0,25.五种不同商品在货架上排成一排,其中,A B 两种必须连排,而,C D 两种不能连排,则不同的排法共有( )A .12种B .20种C .24种D .48种 6.、设12,,,na a a L 是1,2,…,n 的一个排列,把排在ia 的左边且比ia 小的数的个数为ia (i =1,2,…n)的顺序数,如在排列6,4,5,3,2,1中,5的顺序数为1,3的顺序数为0,则在1至 8这8个数的排列中,8的顺序数为2,7的顺序数为3,5的顺序数为3的不同排列的种数为 ( )A 120B 48C 144D 192 7.设随机变量~(2,),~(4,)B p B p ξη若5(1)9P ξ≥=,则(2)P η≥的值为( ) A .3281 B .1127 C .6581D .16818.9.若对任意实数x ,有3322103)2()2()2(-+-+-+=x a x a x a a x 成立,则=++321a a a ( )A .1B .8C .19D .27 10.已知等式4321234x a x a x a x a ++++4321234(1)(1)(1)(1)x b x b x b x b =++++++++,定义映射12341234:(,,,)(,,,)f a a a a b b b b →,则(4,3,2,1)f =( ) A .(1,2,3,4) B .(0,3,4,0) C .(0,3,4,1)-- D .(1,0,2,2)--11.43(1)(1x --的展开式中2x 的系数为( )(A )6- (B )3- (C )0 (D )312.9)1(xx +的展开式中3x 的系数是 (用数字作答)13.10个三好学生名额分到7个班级,每个班级至少一个名额,不同分配方案有 种 14.将全体正整数自小到大一个接一个地顺次写成一排,如第11个数字是0,则从左至右的第2013个数字是 .15.1+3+32+…+399被4除,所得的余数为________.16.写出从a,b,c,d,e 中取出2个元素的所有排列和组合. 17.(8分)某医院有内科医生12名,外科医生8名,现要派5名医生参加赈灾医疗队,则:(1)某内科医生必须参加,某外科医生不能参加,有多少种选法? (2)至少有一名内科医生且至少有一名外科医生参加有几种选法?18.(本小题14分)已知n n x x x )13()(223-+和比的展开式的二项式系数的展开式的系数和大992。

河南省示范性高中罗山高中2016届高三数学复习单元过关练:选修2-2(含解析)1.设()[)[]2,0,12,1,2x x f x x x ⎧∈⎪=⎨-∈⎪⎩,则()20f x dx ⎰的值为( )A. 34 B . 45 C. 56 D. 762.⎰ππ-+22)cos 1(dx x 等于( )A. πB. 2C. 2-πD. 2+π3.若sin 211)i θθ-++是纯虚数(其中i 是虚数单位),且[0,2)θπ∈,则θ的值是( )A 、4π B 、34π C 、54π D 、544ππ或4.若211ai i=--,其中a 是实数,i 是虚数单位,则a= ( )(A )1 (B)2 (C ) 3 (D) -15.若函数mx e y x+=有极值,则实数m 的取值范围是( ) A .m>0 B .m<0 C .m>1 D .m<16.设a R ∈,若函数xy e ax =+,x R ∈,有大于零的极值点,则( ) A 、1a e <- B 、1a >- C 、1a <- D 、1a e>-7.已知3)2(3123++++=x b bx x y 是R 上的单调增函数,则b 的取值范围是() A. 21>-<b b ,或 B. 21≥-≤b b ,或 C. 21<<-b D. 21≤≤-b8.函数f (x )=x ln x 的单调递减区间是 ( ). A.1,e ⎛⎫+∞ ⎪⎝⎭ B. 1,e ⎛⎫-∞ ⎪⎝⎭ C.10,e ⎛⎫ ⎪⎝⎭D .(e ,+∞) 9.若0()3f x '=-,则000()(3)limh f x h f x h h→+--=( )A .3-B .12-C .9-D .6- 10.由直线1y x =+上的一点向圆22680x x y -++=引切线,则切线长的最小值为( )A . 1 B. CD .311.下列推理过程属于演绎推理的为( )A .老鼠、猴子与人在身体结构上有相似之处,某医药先在猴子身上试验,试验成功后B .由22211,132,1353,=+=++=L 得出1+ 235(21)n n +++-=LC .由三角形的三条中线交于一点联想到四面体四条中线(四面体每一个顶点与对面重心的连线)交于一点D .通项公式形如(0)n n a cq cq =≠的数列{}n a 为等比数列,则数列{2}n -为等比数列sin 21(2cos 1)i θθ-++i [0,2)θπ∈θ13.过抛物线y=)(x f 上一点A (1,0)的切线的倾斜角为45°则)1(/f =__________. 14.已知x 为实数,复数22(2)(32)=+-+++z x x x x i 为纯虚数,则x = .15.设20lg ,0(),3,0ax x f x x t dt x >⎧⎪=⎨+≤⎪⎩⎰若((1))1,f f =则5(42)x x a -+-展开式中常数项为 。

高中数学学习材料金戈铁骑整理制作河南省示范性高中罗山高中2016届高三数学(文)复习单元巩固题:必修一 集合与函数的概念(有解析)1.下列各组中的函数)(x f 与)(x g 相等的是( )A. x x f =)(,2)()(x x g =B. 2)(x x f =,x x g =)(C.11)(2+-=x x x f ,1)(-=x x g D. 0)(x x f =,x x x g =)( 2.设{}{}{}1,2,3,4,5,1,2,5,2,3,4U A B ===,则U B C A ⋂= ( )A .φB .{}2C .{}3,4D .{}1,3,4,53.已知集合2{|2},{|230}M x x N x x x =<=--<,则集合MN =( ) A .{|2} x x <- B .{3}x |x >C .{12} x |x -<<D .{23}x |x <<4.已知函数()f x 是定义在(0,+)∞上的单调函数,且对任意的正数,x y 都有()=()+(),f x y f x f y ⋅若数列{}n a 的前n 项和为n S ,且满足(+2) ()=(3) (n ),n n f S f a f N *-∈则n a 为( )A . -1 2nB . nC .21n -D . 13()2n - 5.若集合21M y y x ⎧⎫==⎨⎬⎩⎭,{}1N x y x ==-,那么M N =( )A.()0,+∞B.[)0,+∞C.()1,+∞D.[)1,+∞6.定义在R 上的函数f (x )的图像关于x =1对称,且当x ≥1时,f (x )=3x -1,则有( )A .f 13()<f 32()<⎪⎭⎫ ⎝⎛32fB .f 23()<f 32()<f 13()C .f 32()<f 23()<f 13()D .f 23()<f 13()<f 32()7.集合{}10,log ≠>==a a x y x M a 且,{}10,log ≠>==a a x y y N a 且,则M 与N 的关系中正确的是( )A .N M =B .M NC .N MD .与a 有关 8.已知全集U=R ,集合A={}13>x x ,B={}0log 2>x x ,则A ∪B=( )A .{}0>x xB .{}1>x xC .{}10<<x xD .{}0<x x9.若函数()y f x =的反函数图象过点(15),,则函数()y f x =的图象必过点( )A .(51),B .(15),C .(11),D .(55), 10.集合M={(x ,y )| x >0,y >0},N={(x ,y )| x+y >0,xy >0}则( )A 、M=NB 、M NC 、M ND 、M ⋂N=∅11.已知函数(1)y f x =-的图象关于点(1,0)对称,且当(,0)x ∈-∞时,()()0f x x f x '+<成立(其中()f x '是()f x 的导函数),若0.30.3(3)(3)a f =⋅,(log 3)(log 3)b f ππ=⋅,3311(log )(log )99c f =⋅,则,,a b c 的大小关系是( ) A .a b c >> B .c b a >> C. c a b >> D .a c b >>12.已知全集U =R ,集合{10}A x x =+<,{30}B x x =-<,那么集合()UC A B = (A ){13}x x -≤<(B ){13}x x -<<(C ){1}x x <-(D ){3}x x >13.设集合}35{<<-=x x A ,}42{<<-=x x B ,则=B A _________________ 14.已知f (1,1)=1,f (m ,n )∈N *(m 、n ∈N *),且对任意m 、n ∈N *都有:① f (m ,n+1)= f (m ,n )+2; ② f (m +1,1)=2 f (m ,1).给出以下三个结论:(1)f (1,5)=9;(2)f (5,1)=16;(3)f (5,6)=26.其中正确的个数为15.已知A ={-1,3,2m -1},B ={3,2m }.若B ⊆A ,则实数m = 。
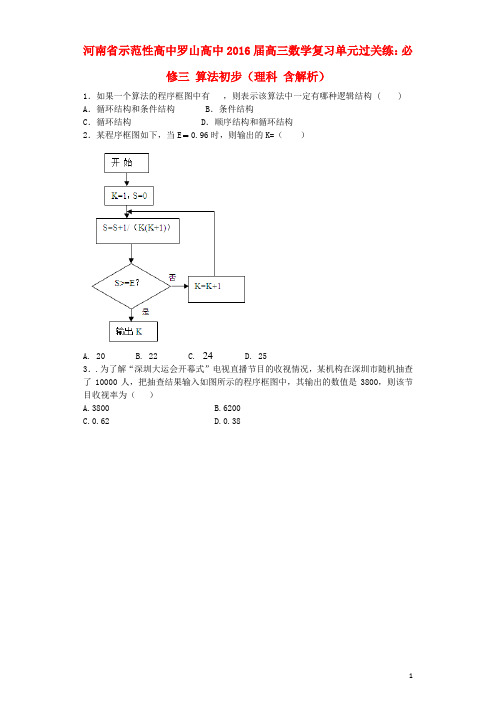
河南省示范性高中罗山高中2016届高三数学复习单元过关练:必修三算法初步(理科含解析)1.如果一个算法的程序框图中有,则表示该算法中一定有哪种逻辑结构 ( ) A.循环结构和条件结构B.条件结构C.循环结构 D.顺序结构和循环结构2.某程序框图如下,当E 0.96时,则输出的K=()A. 20B. 22C. 24D. 253..为了解“深圳大运会开幕式”电视直播节目的收视情况,某机构在深圳市随机抽查了10000人,把抽查结果输入如图所示的程序框图中,其输出的数值是3800,则该节目收视率为()A.3800B.6200C.0.62D.0.384.阅读右面程序框图,任意输入一次(01)x x ≤≤与(01)y y ≤≤,则能输出数对(,)x y 的概率为( ) A.14 B .23 C . 13 D .345.计算机中常用16进制,采用数字0~9和字母A ~F 共16个计数符号与10进制得对应关系如下表:例如用16进制表示D+E =1B ,则(2×F+1)×4=( ) A 6E B 7C C 5F D B06.如图所示程序框图运行后输出的结果为( )开始输出S 结束N 第8题图T ≤10000YT=T+1 S=0 T=1 N S=S+1 Y 观看直播A .36B .45C .55D .56 7.执行如图所示的程序框图,则输出的S 的值是( )A .-1B .23C .32D .48. 如右图所示的算法流程图中(注:“1A =”也可写成“:1A =”或“1←A ”, 均表示赋值语句),第3个输出的数是A .1 B.32 C. 2 D. 529.计算机中常用的十六进制是逢16进1的计数制,采用数字9~0和字母F A ~共16十六进制 0 1 2 3 4 5 6 7 十进制 0 1 2 3 4 5 6 7 十六进制 89 A B C D E F例如,用十六进制表示1E D B +=,则=⨯B A ( ) (A )6E (B )72 (C )5F (D )0B 10..计算机执行下面的程序,输出的结果是( )A .1,3B .4,9C .4,12D .4,811.某程序框图如图,该程序运行后输出的k 的值是( )A .4B .5C .6D .7 12.如果执行右面的程序框图,那么输出的S =( )A .22B .46C .190D .94a =1b =3 a =a +b b =b *a PRINT a ,b END13.下边程序运行后输出的结果为_______________.5x =20y =-IF 0x < THEN3x y =- ELSE3y y =+END IFPRINT x -y ; y -x END14.执行如下图的程序框图,输出s 和n ,则s n +的值为 .15.已知5432()5101051f x x x x x x =+++++,当2x =时,用秦九韶算法求2v =______________.16.图中是一个算法流程图,则输出的=n .17.新课标要求学生数学模块学分认定由模块成绩决定,模块成绩由模块考试成绩和平时成绩构成,各占50%,若模块成绩大于或等于60分,获得2学分,否则不能获得学分(为0分).设计一算法,通过考试成绩和平时成绩计算学分,并画出程序框图.18.由相应的程序框图如图,补充完整一个计算1+2+3+…+100的值的算法.(用循环结构)第一步,设i 的值为_____________. 第二步,设sum 的值为_____________.第三步,如果i≤100执行第_____________步,否则,转去执行第_____________步. 第四步,计算sum +i 并将结果代替_____________. 第五步,计算_____________并将结果代替i. 第六步,转去执行第三步.第七步,输出sum 的值并结束算法.19.求324,243,135三数的最大公约数. 20.设计一个用有理数数幂逼近无理指数幂的算法,画出算法的程序框图.21.(本小题满分14分)下面是利用UNTIL 循环设计的计算13599⨯⨯⨯⨯L 的一个算法程序. S =1 i=1 DO① i=i+2LOOP UNTIL ② PRINT S END(Ⅰ)请将其补充完整,并转化为WHILE 循环; (Ⅱ)绘制出该算法的流程图. 22.已知某算法的流程图如图所示,若将输出的(x,y 值依次记为(x1,y1),(x2,y2),……(x n,y n),…(Ⅰ)若程序运行中输出的一个数组是(9 , t),则t = ;(Ⅱ)程序结束时,共输出(x , y )的组数为;(Ⅲ)写出流程图的程序语句.参考答案1.B【解析】解:因为如果一个算法的程序框图中有 ,则表示该算法中一定有条件结构 选B 2.C 【解析】试题分析:S 的初始值为0,步长为1,根据算法得,111110.9624.1223(1)1S k k k k =+++=-≥⇒≤⨯⨯⨯++L 故选C 。

高中数学学习材料马鸣风萧萧*整理制作河南省罗山高中2016届高三数学复习精选练习(含解析):集合间的基本关系和基本运算(2)1、设集合)2013,,3,2}(11,1|{2 =≤≤+==k t kkt kt x x A k ,则所有k A 的交集为( )(A) ∅ (B) }2{ (C) ]25,2[ (D) ]201312013,2[2+【答案】C2、⎪⎩⎪⎨⎧∈+-∈=Mx x x Px x x f ,2,)(2,M P ,是非空数集且P M =∅,记}),({P x x f y y P ∈==Ω,又记}),({M x x f y y M ∈==Ω,若实数a 满足[3,]PM a =-且]32,3[--=ΩΩa M P ,其中3->a ,实数a 的取值范围是( )A.}3{B.),3[+∞C.]6,0(D.]6,3[ 【答案】A3、设集合{}121,2,3,4,5,6,,,k M S S S =都是M 的含有两个元素的子集,且满足对任意的{}{}{},,,,,1,2,,i i i j j j S a b S a b i j i j k ==≠∈()min ,min ,j j i i i i j j a b a b b a b a ⎧⎫⎧⎫⎪⎪≠⎨⎬⎨⎬⎪⎪⎩⎭⎩⎭其中{}min ,x y 表示两个数,x y 的较小者,则k 的最大值是( ) A 、10 B 、11 C 、12 D 、13 【答案】B 4、若1122m x m -<≤+(其中m 为整数),则称m 为离实数x 最近的整数,记作{}x ,即{}m x =.设集合(){}{},|,A x y y x x x R ==-∈,(){}2,|,B x y y axbx x R ==+∈,若集合B A 的子集恰有两个,则b a ,的取值不可能是( ) A .1,5==b a B .1,2-=-=b a C . 1,4-==b a D .4,1a b =-= 【答案】C5、已知集合{}{}2|320,|log 42x A x x x B x =-+===,则A B =( )A.{}2,1,2-B.{}1,2C.{}2,2-D.{}2 【答案】B【解析】A={1,2},由log 42x =,得24x =,又因为0x >,所以2x =.故B={2}.则{}1,2A B =.6、全集U={1,2,3,4,5},集合M={1,4},N={1,3,5},则U NC M =( )A.{3,5}B.{1,5}C.{4,5}D.{1,3}【答案】A7、已知全集U =R ,集合M ={y |y =x 2-1,x ∈R },集合,则(M )∩N=( )A .(-2,-1)B .[-2,-1)C .[-2,1)D .[-2,1] 【答案】B【解析】集合M 是函数的值域,M ={y |y ≥-1},M ={y |y <-1};集合N 是函数的定义域,N ={x |-2≤x ≤2},所以(M )∩N =[-2,-1).故选B.8、设A 、B 是两个集合,定义M *N ={x |x ∈M 且x ?N }.若M ={y |y =log 2(-x 2-2x +3)},N ={y |y =,x ∈[0,9]},则M *N =( )A .(-∞,0]B .(-∞,0)C .[0,2]D .(-∞,0)∪(2,3] 【答案】B【解析】y =log 2(-x 2-2x +3)=log 2[-(x +1)2+4]∈(-∞,2],N 中,∵x ∈[0,9], ∴结合定义得:M *N =(-∞,0).9、已知集合22{(,)|23}M x y x y =+=,{(,)|}N x y y mx b ==+,若对所有的m R ∈,均有M N φ≠,则b 的取值范围是( )A .66[,]22-B .66(,)22-C . 2323(,]33-D .2323[,]33-【答案】A 10、设⎭⎬⎫⎩⎨⎧∈<<=Z x x x A ,521|,{}a x x B >=|,若B A ⊆,则实数a 的取值范围是( )A .21<a B .21≤a C .1≤a D .1<a【答案】D11、设集合{2,04,},{2,}nA x x n nB x x n n ==<<∈==∈Z Z ,则AB 为( )A .{1,2,4,8,16}B .{1,2,4,8}C .{2,4,8}D .{2,4} 【答案】C【解析】由题可知{2,4,8}A =,{}B =偶数,因此{2,4,8}A B =, 故选C . 12、已知集合{}1,2S =,集合{}T a =,∅表示空集,如果ST S =,那么a 的值是( )A .∅B .1C .2D .1或2 【答案】C13、已知集合A={1,2,3,4},满足{1,2}⊆B ⊆A 的集合B 有 个. 【答案】4【解析】∵集合A={1,2,3,4}, 又∵{1,2}⊆B ⊆A∴B={1,2}或B={1,2,3}或B={1,2,4}或B={1,2,3,4} 故满足条件的集合B 共有4个14、集合A={x ∈N|1≤x ≤3}的真子集个数是 .【答案】7【解析】∵集合A={x ∈N|1≤x ≤3}={1,2,3},∴集合A 的真子集是:∅,{3},{1},{2},{3,1},{3,2},{1,2}, 共有7个,15、集合A={2,3}的真子集个数是 . 【答案】3 【解析】16、满足{1}⊂A ⊆{1,2,3}的集合A 的个数是 . 【答案】3【解析】A={1}⋃B ,其中B 为{2,3}的子集,且B 非空.显然这样的集合A 有3个,即A={1,2}或{1,3}或{1,2,3}.17、已知全集U R =,集合{|22}A x x =-<≤,{|1}B x x =>,{|}C x x c =≤ (1)求,AB A (U B ),(U A )B ; (2)若,A C ≠∅求的取值范围.【答案】(1){}(){}(){}2,21,2U U A B x x A C B x x C A B x x ⋃=>-⋂=-<≤⋂=>; (2)2c >-.思路点拨:(1)根据题意集合间的并集为两个集合中所有元素组成的集合所以{}2A B x x ⋃=>-,集合U C B 为集合B 在U 中的补集即在集合U 中把含有集合B 的元素取掉剩余的元素组成的集合,所以,{}1U C B x x =≤,同理{}{}1,2.2U U C B x x C A x x x =≤=≤->或,交集为两个集合公共元素组成的集合,继而得到所求结果;(2)因为集合,A B 为空集,所以集合,A B 没有公共元素,所以在上数轴上在2-的左侧,所以2c <-. 试题解析:(1)集合{|22}A x x =-<≤,{|1}B x x =>,{|2}A B x x ∴=>-{}{}1,2.2U U C B x x C A x x x =≤=≤->或∴A (U B ){|21}x x =-<≤(U A )B {|2}x x =>(2),{|22},A C A x x ≠∅=-<≤{|}C x x c =≤2c ∴>-考点:1.集合间的交集,并集,补集;2.数轴.18、已知集合A={x ∈R|x 2+4x=0},B={x ∈R|x 2+2(a+1)x+a 2-1=0},如果A∩B=B,求实数a 的取值范围.【答案】a ≤-1或a=1思路点拨:集合A={0,-4},两个元素,而集合A∩B=B,所以B 是集合A 的子集,那么集合B 有四种可能,我们分类讨论就行了. 试题解析:∵B B A =⋂∴B ⊆A,∵A={0,-4},∴B=Φ,或B={0},或B={-4},或B={0,-4}分由x 2+2(a +1)x +a 2-1=0得△=4(a +1)2—4(a 2-1)=8(a +1) ①当a <-1时,则△<0,此时B=φ⊆A ,显然成立; ②当a=-1时△=0,此时B={0}⊆A ; ③当a >-1时△>0,要使B ⊆A ,则A=B ∴0,-4是方程x 2+2(a+1)x+a 2-1=0的两根 ∴22(1)410a a -+=-⎧⎨-=⎩,解之得a=1综上可得a ≤-1或a=1考点:二次函数分类讨论19、设集合{|37},{|210},{|}A x x B x x C x x a =≤≤=<<=<,全集为实数集R (1)求:AB ;()R C A B ;(2)若φ≠C A ,求a 的取值范围【答案】(1){210}x x <<,{}10732|<<<<x x x 或;(2)3>a ;思路点拨:(1)已知集合A ,集合B ,由补集的定义易得{210}A B x x ⋃=<<,由{}a x x C <=|,得到{3,7}R C A x x x =<>或,因此{}10732|)(<<<<=x x x B A C R 或 ;(2)若φ≠C A ,则集合A 与集合C 有交集,将集合A 与集合C 分别在数轴上表示出来,显然有3>a ; 试题解析:(1){210}A B x x ⋃=<<{3,7}R C A x x x =<>或{}10732|)(<<<<=x x x B A C R 或(2)若φ≠C A ,则集合A 与集合C 有交集,集合A 若有交集,则必然有3>a ; 考点:集合的交并补运算20、已知集合{}73|<≤=x x A ,{}102|<<=x x B ,{}|5C x a x a =<<+. (1)求B A ⋃,B A C R ⋂)(; (2)若C B ⊆,求a 的取值范围.【答案】(1)}102{<<=⋃x x B A ,B A C R ⋂)(}10732{<≤<<=x x x 或;(2)]5,2[ 思路点拨:首先利用并集定义求出B A ⋃,再利用补集定义求出A C R ,和B 找交集即可;第二步利用数轴表示集合B 、C ,使B C ⊆,写出需要满足的条件,解不等式组即可.试题解析:(1)}102{<<=⋃x x B A ,=A C R {}|37x x x <≥或,则B AC R ⋂)(}10732{<≤<<=x x x 或(2)由于B C ⊆,即:}102{}5{<<⊆+<<x x a x a x ,在数轴上表示出符合条件要求的两个集合,需要满足522105≤≤⇒⎩⎨⎧≥≤+a a a ,a 的取值范围是]5,2[考点:1.集合的交、并、补运算;2.子集的定义; 21、已知集合2{|150}A x x px =-+=,2{|0}B x x ax b =--=,{2,3,5}A B =,{3}A B =,求,,p a b 的值.【答案】8,5,6p a b ===- 思路点拨:根据{3}AB =可知3A ∈进而求得p 的值,解得集合{}3,5A =,又因为{2,3,5}A B =,{3}A B =,可知{}2,3b =,由韦达定理求得,a b 的值.试题解析:2{|150}A x x px =-+=,2{|0}B x x ax b =--=,{3}A B =3A ∴∈,3B ∈233150p ∴-⨯+=,8p ∴=. 2{|8150}{3,5}A x x x ∴=-+==.又{2,3,5}A B =,{3}A B =,{2,3}B ∴=∴2和是方程20x ax b --=的两根.235a ∴=+=,23b -=⨯即6b =-..考点:1.集合的交集,并集,补集运算;2.韦达定理. 22、已知集合}{{}121,01A x a x a B x x =-<<+=<<.(Ⅰ)若12a A B =时,求; (Ⅱ)若AB φ=,求实数a .【答案】(1){}10|<<x x ;(2)[)1,2,2⎛⎤-∞-+∞ ⎥⎝⎦.思路点拨:(1)代入21=a ,化简集合A,B ,再利用数轴求其交集;(2)利用数轴进行求解.解题思路:在处理连续数集的关系或运算时,往往利用数形结合思想,借助数轴进行求解.试题解析:(Ⅰ)当12a =时{}12,012A x x B x x ⎧⎫=-<<=<<⎨⎬⎩⎭{}01A B x x ∴=<<(Ⅱ)当2121a a a ≤--≥+时,从而A φ=故A B φ=符合题意2a ∴≤-当2a >-时,由于A B φ=,故有11210a a -≥+≤或解得1222a a ≥-<≤-或综上所述实数a 的取值范围是[)1,2,2⎛⎤-∞-+∞ ⎥⎝⎦.考点:1.集合的运算;2.数形结合思想.。
罗山高中2013届毕业班第三轮第一次模拟考试数学(理科)一、 选择题(本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,只有一项是符合题目要求的.) 1. 集合{}1,M z z z =≤∈C ,1,2N z z bi b ⎧⎫==+∈⎨⎬⎩⎭R ,则M N =∅ ,则实数b 的取值范围是 ( )A.3(,(,)-∞+∞ B. 3(,[,)-∞+∞C.(D. [ 2. 已知()|2||4|f x x x =++-的最小值为n ,则二项式1()n x x-展开式中2x 项的系数为( ) A .15 B .15- C .30 D .30-3. 设函数()sin()(0)()cos(2)(||)42f x xg x x ππωωφφ=+>=+≤与函数的对称轴完同,则φ的值为( )A .4πB .-4π C .2π D .-2π 4. 已知xdx N dx x M ⎰⎰=-=2012cos ,1π,由如右程序框图输出的=S ( ) A.1 B.2πC.4πD.1-5. 在平面直角坐标系xoy 中,圆C 的方程为228150x y x +-+=,若直线2y kx =-上至少存在一点,使得以该点为圆心,1为半径的圆与圆C 有公共点,则k 的最大值为( ) A .2 B .43 C .23D . 3 6.在ABC ∆中,内角,,A B C 所对的边分别为,,a b c ,其中120,1Ab ==,且ABC ∆面积则sin sin a bA B+=+( )AB.3C.7. 已知函数5()ln ,()log ,()lg f x x g x x h x x ===,若直线222()y m m m =-+-∈R 与(),(),()y f x y g x y h x ===图像交点的横坐标分别为,,a b c ,则( )A.a b c <<B.c b a <<C.c a b <<D.b c a <<8.下列四个命题中,错误的个数是( ) ①1x e dx e =⎰;②设回归直线方程为ˆ2 2.5,yx =-当变量x 增加一个单位时,y 大约减少2.5个单位; ③已知ξ服从正态分布N (0,2σ),且(20)0.4P ξ-≤≤=,则:(2)0.1P ξ>= ④对于命题:"0":"0"11x x p p x x ≥⌝<--则 A .0个B .1个C .2个D .3个9.已知 y x ,满足⎪⎩⎪⎨⎧≥++-≤+≥0242c y x y x x ,且目标函数y x z +=3的最小值是5,则z 的最大值是( ) A . 9 B. 10 C. 11 D .12 10. 定义在R 上的函数)(x f y =,对任意不等的实数1x ,2x 都有0))](()([2121<--x x x f x f 成立,又函数)1(-=x f y 的图象关于点)0,1(对称,若不等式0)2()2(22≤-+-y y f x x f 成立,则当41≤≤x 时,xy的取值范围是( ) A.1[,)2-+∞ B.(,1]-∞ C.1[,1]2- D.1,12⎛⎫- ⎪⎝⎭11. 已知直三棱柱ABC -A 1B 1C 1的各棱长均为1,棱BB 1所在直线上的动点M 满足1BB λ=,AM 与侧面BB 1C 1C 所成的角为θ,若⎥⎦⎤⎢⎣⎡∈2,22λ,则θ的取值范围是( ) A .⎥⎦⎤⎢⎣⎡6,12ππ B .⎥⎦⎤⎢⎣⎡4,6ππ C .⎥⎦⎤⎢⎣⎡3,4ππ D .⎥⎦⎤⎢⎣⎡125,3ππ 12.在曲线C:)0(222 x y x =-上任取A,B 两点,则OB OA ∙的最小值( )A .2 B.4 C.2 D.22二、填空题:(每小题5分,共20分,请将符合题意的最简答案填在题中横线上) 13.某商场在庆元宵促销活动中,对元宵节9时至14时的销售额进行统计,其频率分布直方图如图所示,已知9时至10时的销售额为2.5万元,则11时至12时的销售额为 万元.14.一个几何体的三视图如上图所示,且其左视图是一个等边..三角形,则这个几何体的体积为 .15. 已知点P 是抛物线24y x =上的动点,点P 在y 轴上的射影是M ,点A 的坐标是(4,a ),则当||4a >时, ||||PA PM +的最小值是 . 16.观察下列等式:1535522C C +=-, 1597399922C C C ++=+,159131151313131322C C C C +++=-,1591317157171717171722C C C C C ++++=+,………由以上等式推测到一个一般的结论:对于*n N ∈,4141n n C ++++=三、解答题:(解答题必须写出解题步骤和必要的文字说明,共70分)17. (本小题满分12分)设数列}{n a 的前n 项和为n S ,101=a ,1091+=+n n S a .⑴求证:}{lg n a 是等差数列. ⑵设n T 是数列⎭⎬⎫⎩⎨⎧+))(lg (lg 31n n a a 的前n 项和,求使)5(412m m T n ->对所有的*∈N n 都成立的最大正整数m 的值 18.(本小题满分12分)某学校为了研究学情,从高三年级中抽取了20名学生三次测试的数学成绩和物理成绩,计算出了他们三次成绩的平均名次如下表:(Ⅰ)对名次优秀赋分2,对名次不优秀赋分1.从这20名学生中随机抽取2名学生,用ξ表第14题图示这2名学生两科名次赋分的和,求ξ的分布列和数学期望;(Ⅱ)根据这次抽查数据,列出2×2列联表,能否在犯错误的概率不超过0.025的前提下认19. (本小题满分12分)如图1, 在直角梯形ABCD 中, 90ADC ∠=︒,//CD AB ,4,2AB AD CD ===,M 为线段AB 的中点. 将ADC ∆沿AC 折起,使平面ADC ⊥平面ABC ,得到几何体D ABC -,如图2所示. (1)求证:BC ⊥平面ACD ;(2)求二面角A CD M --的余弦值.20(题满分12分)已知椭圆2222:1(0)x y C a b a b +=>>的离心率为12,以原点为圆心,椭圆的短半轴长为半径的圆与直线0x y -+=相切,过点P (4,0)且不垂直于x 轴的直线l 与椭圆C 相交于A 、B 两点。
高中数学学习材料(灿若寒星精心整理制作)河南省罗山高中2016届高三数学复习精选练习(含解析):集合与集合的表示方法(2)1、从集合{1,2,3,…,10}中选出5个数组成的子集,使得这5个数中任何两个的和不等于11,这样的子集共有()A.10个B.16个C.20个D.32个【答案】D【解析】将和等于11放在一组:1和10,2和9,3和8,4和7,5和6.从每一小组中取一个,有C21=2种,共有2×2×2×2×2=32.故选D.2、已知a∈R,设集合A={x||x-1|≤2a-a2-2},则A的子集个数共有()A.0个B.1个C.2个D.无数个【答案】B【解析】因为2a-a2-2=-2a2+2a-2=-(a-1)2-1≤-1,所以|x-1|≤2a-a2-2无解,即集合A=∅,则集合A的子集个数只有一个是本身,即∅.故选B.3、已知非空集合P⊂{3,4,6},P中至多有一个偶数,则这样的集合P共有()A.2个B.4个C.5个D.6个【答案】D【解析】由于集合p为{3,4,6}的子集,则p可以为{3,4,6},{3},{4},{6},{3,4},{3,6},{4,6},∅;又因为p中最多有一个偶数即有一个或没有偶数的有{4},{3},{6},{3,4},{3,6},∅共有6个.故选D.4、若集合A1,A2满足A1⋃A2=A,则记[A1,A2]是A的一组双子集拆分.规定:[A1,A2]和[A2,A1]是A的同一组双子集拆分,已知集合A={1,2},那么A的不同双子集拆分共有()A.8组B.7组C.5组D.4组【答案】D5、已知集合A={2,3},则集合A的子集个数是()A.1个B.2个C.3个D.4个【答案】D【解析】集合A={2,3}的子集分别是:∅,{2},{3},{2,3},共有4个,故选D.6、集合{x∈z||x|<3|}的真子集的个数是()A.16B.15C.32D.31【答案】D【解析】集合A={x∈z||x|<3|}={-2,-1,0,1,2},共5个元素.真子集的个数是25-1=31个.故选D.7、已知A⊆{0,1,2,3},且A中至少有一个奇数,则这样的集合A共有()A.11个B.12个C.15个D.16个【答案】B【解析】根据题意,A中至少有一个奇数,包含两种情况,A中有1个奇数或2个奇数,若A中含1个奇数,有C21×22=8,A中含2个奇数:C22×22=4,由分类计数原理可得.共有8+4=12种情况;故选B.8、已知集合P={x|x2-2x+1=0,x∈R},则集合P的子集个数是()A.1B.2C.4D.8【答案】B【解析】由x2-2x+1=0解得,x=1,∴A={1},∴A的子集有{1}和?,即子集的个数为2,故选B.9、2009年国庆阅兵现场60名标兵担负着定位和武装警戒的任务,是受阅部队行进的参照物,同时还要以良好的军姿军容展现国威军威.如果将每一名标兵看作一个元素,那么60名标兵形成的集合的子集的个数是()A.120B.60C.260D.260-1【答案】C【解析】由60名标兵形成的集合{a,b,c,…}的子集有:?,{a},{b},{c},{a,b}…{a,b,c},…共260个.故选C.10、对于任意两个正整数,定义某种运算m、n;当m、n都为正偶数或正奇数时,m n=m+n;当m、n中一个为正奇数,另一个为正偶数时,m n=mn.则在上述定义下,M={(x,y)|x y=36,x∈N*,y∈N*},集合M中元素的个数为A.40B.48C.39D.41【答案】D11、已知集合M={x| x2<4},N={x| x2-2x-3<0},则集合M⋂N等于()A.{x|x<2}B.{x|x>3}C.{x|-1<x<2}D.{x|2<x<3}【答案】C12、已知集合A={a},则下列各式正确的是()A.a⊆AB.a∈AC.a∉AD.a=A【答案】B【解析】∵集合A={a},∴a∈A故选B13、非负整数a,b满足|a-b|+ab=1,记集合M={(a,b)},则M的元素的个数为.【答案】3【解析】∵a,b是非负整数∴|a-b|≥0的整数,ab≥0的整数.又∵|a-b|+ab=1,∴1-ab=|a-b|≥0的整数.∴0≤ab≤1的整数.取a=0,b=1;a=1,b=0;a=1,b=1皆满足|a-b|+ab=1,∴集合M={(a,b)}的元素的个数为3个.14、已知集合A={0,1},B={2},定义集合M={x|x=ab+a-b,a,b∈A或B},则M中所有元素之和为.【答案】7【解析】当a∈A,b∈B时,取a=0,b=2,则x=-2;取a=1,b=2,则x=1;当a∈B,b∈A时,取a=2,b=0,则x=2;取a=2,b=1,则x=3;当a,b∈A时,取a=0,b=1,则x=-1;取a=1,b=0,则x=1;取a=b=0,则x=0;取a=b=1,则x=1;当a,b∈B时,取a=b=2,则x=4,所以M={-2,-1,0,1,2,3,4},其各元素之和为7.15、已知M={x∈R|x≥2},a=22,则下列四个式子①a∈M;②{a}⊆M;③a⊆M;④{a}⋂M=22,其中正确的是.(填写所有正确的序号).【答案】①②【解析】16、已知集合A={1,m+2,m2+4},且5∈A,则m= .【答案】3或1.【解析】因为5∈A,所以m+2=5或m2+4=5,解得m=3,或m=±1.验证知,当m=-1时,A={1,1,5},此时集合A不成立.所以m=3或1.故答案为:3或1.17、若集合{x,xy,lgxy}={0,|x|,y},则log8(x2+y2)的值为多少.【答案】根据集合中元素的互异性,在第一个集合中,x≠0,第二个集合中,知道y≠0,∴第一个集合中的xy≠0,只有lg(xy)=0,可得xy=1①,∴x=y②或xy=y③.由①②联立,解得x =y =1或x =y =-1,若x =y =1,xy =1,违背集合中元素的互异性,若x =y =-1,则xy =|x|=1,从而两个集合中的元素相同.①③联立,解得x =y =1,不符合题意.∴x =-1,y =-1,符合集合相等的条件.因此,log 8(x 2+y 2)=log 82=13. 18、若1∈{x|x 2+px +q =0},2∈{x|x 2+px +q =0},求p 、q 的值。
河南省示范性高中罗山高中2016届高三数学复习单元过关练:选修1-2(含解析)1.i 是虚数单位,则复数的实部为( )A . 2B .1C .1D .22.复数z 1=a +2i ,z 2=-2+i ,如果|z 1|<|z 2|,则实数a 的取值范围是( ). A .-1<a<1 B .a>1 C .a>0 D .a<-1或a>1 3.设i 是虚数单位,复数21iz i=+,则|z |=( ) A .1 B 23.24.“指数函数(1)xy a a =>是增函数,(1)y x αα=>是指数函数,所以y x α=(1)α>是增函数”,在以上演绎推理中,下列说法正确的是( ) A .推理完全正确 B .大前提不正确 C .小前提不正确 D .推理形式不正确 5.下列推理是归纳推理的是( )A.A,B 为定点,动点P 满足|PA|+|PB|=2a>|AB|,则P 点的轨迹为椭圆B.由a 1=1,a n =3n-1,求出S 1,S 2,S 3,猜想出数列的前n 项和S n 的表达式C.由圆x 2+y 2=r 2的面积πr 2,猜想出椭圆22221x y a b+=的面积S=πabD.以上均不正确6.复数z =32ii-++的共轭复数是 ( ) (A )2+i (B )2-i (C )-1+i (D )-1-i 7.用反证法证明某命题时,对结论:“自然数a ,b ,c 中恰有一个偶数”正确的反设为( )A .a ,b ,c 中至少有两个偶数B .a ,b ,c 中至少有两个偶数或都是奇数C .a ,b ,c 都是奇数D .a ,b ,c 都是偶数8.已知i 是虚数单位,则复数2201411i z i i +⎛⎫=+ ⎪-⎝⎭的模为( )A .1B 2.2 D .49.(2012•湛江二模)通过随机询问110名大学生是否爱好某项运动,得到如下的列联 男 女 总计 爱好 40 20 60 不爱好 20 30 50 总计6050110由上表算得k ≈7.8,因此得到的正确结论是( )A.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”B.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”C.有99%以上的把握认为“爱好该项运动与性别有关”D.有99%以上的把握认为“爱好该项运动与性别无关”10.某商场为了了解毛衣的月销售量y (件)与月平均气温)(C x ︒之间的关系,随机统计了某4个月的月销售量与当月平均气温,其数据如下表: 月平均气温)(C x ︒ 17 13 8 2 月销售量y (件)24334055由表中数据算出线性回归方程ˆy bx a =+中的b =2-,气象部门预测下个月的平均气温约为C ︒6,据此估计该商场下个月毛衣销售量约为( )件.A .46B .40C .38D .58 11.执行如图的程序框图,输出的T=( )A.30 B .25 C .20 D .1212.记123k k k kk S n =++++L ,当1,2,3k =L ,时,观察下列等式:2321211111,22326S n n S n n n =+=++, 432543*********,42452330S n n n S n n n n =++=++-,6542515,212S An n n Bn =+++L ,可以推测A-B 等于( )A .23B .13C .14D .1213.设复数122,12z i z i =+=+,在复平面的对应的向量分别为,OA OB u u u v u u u v,则向量AB u u u v 对应的复数所对应的点的坐标为____________.14.i 是虚数单位,复数的虚部为_________.15.观察下列式子:1,121++,12321++++,1234321++++++,⋅⋅⋅,由以上可推测出一个一般性结论:对于n *∈N ,1221n ++⋅⋅⋅++⋅⋅⋅++的和= .开始 S=0,T=0,n=0T>S S=S+5 n=n+2T=T+n输出T结束是否16.复数(1)(1)2i i z i+-=在复平面上对应的点的坐标为.17.(本小题满分10分)已知复数22(232)(32)i z m m m m =--+-+. (Ⅰ)当实数m 取什么值时,复数z 是纯虚数;(Ⅱ)当0m =时,化简252iz z ++.18.已知正数c b a ,,成等差数列,且公差0≠d ,用反证法求证:cb a 1,1,1不可能是等差数列。
河南省示范性高中罗山高中2016届高三数学复习单元过关练:必修一 函数的应用(理科 含解析)1.函数2)(-+=x e x f x 的零点所在的一个区间是( ). A 、)1,2(-- B 、)0,1(- C 、)1,0( D 、)2,1(2.设函数lg |2|,2()1,2x x f x x -≠⎧=⎨=⎩,若关于x 的方程0)()(2=++c x bf x f 恰有5个不同的实数解12345,,,,x x x x x ,则12345()f x x x x x ++++等于 ( ) A .0 B .2lg2C .3lg2D .l3.当[2,1]x ∈-时,不等式3243mx x x ≥--恒成立,则实数m 的取值范围是( )(A )9[6,]8-- (B )[6,2]-- (C )[5,3]-- (D )[4,3]--4.函数xx x f 2ln )(-=的零点所在的大致区间是 ( ) A 、)2,1( B 、)3,2( C 、)1,1(e和)4,3( D 、),(+∞e5.函数1()22xf x e x =+-的零点所在的区间是( )A .1(0,)2B .1(,1)2C .(1,2)D .(2,3)6.函数33)(3--=x x x f 有零点的区间是( )A .(- 1 ,0) B.(0,1) C.(1,2) D.(2,3)7.函数23()log (2)(0)f x x x x=+->的零点所在的大致区间是( )A .(0,1)B .(1,2)C .(2,e )D .(3,4) 8.函数3()log 3f x x x =+-的零点所在的区间是( )A 、()1,0B 、()2,1C 、()2,3D 、()+∞,39..设函数()0)f x a =<的定义域为D ,若所有点))(,(t f s ),(D t s ∈构成一个正方形区域,则a 的值为( )A .2-B .4-C .6-D .8-10.设)(x f 是定义在R 上的偶函数,且)2()2(x f x f -=+,当[]0,2-∈x 时,1)22()(-=xx f ,若在区间)6,2(-内关于x 的方程0)2(log )(=+-x x f a ,恰有4个不同的实数根,则实数a )1,0(≠>a a 的取值范围是( )A.,1)41( B.(1,4) C. (1,8) D.)(8,+∞ 11.(原创)函数x x g 2log )(= )21(>x ,关于x 的方程2()()230g x m g x m +++=恰有三个不同实数解,则实数m 的取值范围为( ) A.(,4(4)-∞-⋃++∞ B.(4-+ C .34(,)23-- D .34,23⎛⎤-- ⎥⎝⎦ 12.已知函数21()(,g x a x x e e=-≤≤e 为自然对数的底数)与()2ln h x x =的图象上存在关于x 轴对称的点,则实数a 的取值范围是( )A .21[1,2]e + B .2[1,2]e - C .221[2,2]e e+- D .2[2,)e -+∞13. 设函数()f x 的定义域为D ,若存在非零实数k 使得对于任意x D ∈,有()()f x k f x +≥,则称()f x 为D 上的“k 调函数”.如果定义域是[1,)-+∞的函数2()f x x =为[1,)-+∞上的“k 调函数”,那么实数k 的取值范围是___▲ .14.函数f(x)=ln x -11x -在区间(k ,k +1)(k∈N *)上存在零点,则k 的值为________. 15.直线b x y +=与曲线29y x -=恰有一个公共点,则b 的取值范围是 .16.若关于x 的方程2xkx =有四个不同的实数解,则实数k 的取值范围是 .17.已知函数⎪⎩⎪⎨⎧-≤++=。