UG有限元分析第8章

ug有限元分析教程有限元分析是一种数值计算方法，用于求解工程结构或物理问题的数学模型。

它将连续的解析问题离散化成有限数量的子域，并在每个子域上进行数值计算，最终得到整个问题的解。

本教程将介绍有限元分析的基本原理和应用方法。

1. 有限元网格的生成有限元分析的第一步是生成适合问题的有限元网格。

网格是由许多小的单元组成，如三角形、四边形或六边形。

生成网格的方法有很多种，如三角剖分、矩形划分和自适应网格等。

2. 定义有限元模型在定义有限元模型时，需要确定问题的几何形状、边界条件和材料性质。

几何形状可以通过几何构造方法来描述，边界条件包括固支、力和热边界条件等。

材料性质可以通过弹性模量、热传导系数和热膨胀系数等参数来描述。

3. 选择合适的有限元类型根据具体的问题，选择合适的有限元类型。

常见的有限元类型包括一维线性元、二维三角形单元和二维四边形单元等。

使用不同的有限元类型可以更好地逼近实际问题的解。

4. 构造有限元方程有限元分析的核心是构造线性方程组。

根据平衡方程和边界条件，将整个问题离散化为有限个子问题，每个子问题对应于一个单元。

然后，根据单元间的连续性，将所有子问题组合成一个总的方程组。

5. 解算有限元方程通过求解线性方程组，可以得到问题的解。

求解线性方程组可以使用直接方法或迭代方法。

常见的直接方法包括高斯消元法和LU分解法，迭代方法包括雅可比迭代法和共轭梯度法等。

6. 后处理结果在求解得到问题的解后，可以进行后处理结果。

后处理包括计算力、应变和位移等物理量，以及绘制图表和动画。

有限元分析是一种强大的数值方法，广泛应用于结构力学、流体力学、热传导和电磁场等领域。

它在解决复杂问题和优化结构设计方面发挥着重要作用。

通过学习有限元分析，您可以更好地理解结构的行为，并提高工程设计的准确性和效率。

UG有限元分析什么是有限元分析有限元分析（FEA）是一种计算机辅助工程（CAE）方法，用于解决复杂工程问题。

它通过将结构或物体离散化为有限数量的子区域（有限元），并在每个子区域内确定适当的物理模型，从而近似求解连续结构中的应力、位移和其他物理特性。

有限元分析广泛应用于工程设计、结构分析、强度校核等领域。

UG(Unigraphics)是一款由西门子公司开发的集成化CAD/CAM/CAE软件。

它具有强大的建模和模拟功能，提供了一套完整的有限元分析工具，用于分析产品设计在各种载荷下的行为和性能。

UG有限元分析模块以其高度精确的计算结果和先进的求解算法而受到广泛的认可和应用。

UG有限元分析的优势1. 稳定性和准确性UG有限元分析采用了现代化的数值计算方法和稳定的数学模型，确保结果的准确性和可靠性。

它能够捕捉复杂结构的精细细节，并提供准确的应力和位移预测，帮助工程师做出准确的决策和优化设计。

2. 模拟功能的丰富性UG提供了丰富的分析类型和功能选项，使工程师能够模拟各种不同条件下的结构行为。

它支持静态分析、动态分析、热分析、疲劳分析等多种分析类型，以及多种材料模型和加载条件的设置，可满足不同工程需求的模拟分析。

3. 建模和后处理的高效性UG具有强大的建模工具和用户友好的界面，使建模过程变得高效和便捷。

用户可以通过简单的操作创建复杂的几何模型，并将其转化为有限元模型。

后处理工具提供了丰富的结果显示和分析功能，可对分析结果进行可视化处理，便于工程师对结果的理解和评估。

4. 与其他模块的集成性作为一款集成化的软件，UG有限元分析模块与UG其他模块（如CAD和CAM）的紧密集成，提供了全面的产品设计和工程分析解决方案。

它可以自动获取CAD模型的几何和材料信息，并将分析结果应用于后续的产品开发和制造过程中。

UG有限元分析的应用UG有限元分析在各个行业和领域都有广泛的应用，以下是一些典型的应用场景：1. 结构分析UG可以帮助工程师进行结构强度和刚度分析，对结构的载荷和约束条件进行预测和评估。

UG有限元分析教程有限元分析（Finite Element Analysis，FEA）是一种计算方法，用于求解连续介质力学问题。

UG作为一款常用的三维CAD软件，也提供了相应的有限元分析功能，下面将介绍UG有限元分析的基本流程和步骤。

首先，建立几何模型是有限元分析的第一步。

在UG中，可以通过绘制线与曲线、创建体与表面等操作，构建出所需的几何形状。

在建模过程中，需要注意几何模型的准确性和合理性，以保证模拟结果的可靠性。

然后，进行网格划分。

有限元分析将几何模型离散化为多个小单元，每个小单元称为网格，通过将整个模型划分为有限个网格单元，可以更容易地对模型进行数值计算。

在UG中，可以选择不同的网格划分算法和参数设置，以求得较为合适的网格划分结果。

接下来，定义边界条件和加载条件。

在有限元分析中，需要对模型的边界进行约束和加载，以模拟真实的工程环境。

在UG中，可以通过选择特定面或边进行边界条件设置，例如固定边界条件、约束边界条件等。

同时，还可以对特定面或边进行加载条件设置，如施加力、施加压力等。

完成边界条件和加载条件的定义后，即可进行求解。

在UG中，可以通过调用有限元分析求解器进行计算。

求解过程中，UG会对模型进行离散化计算，并得到相应的应力、应变等结果。

求解的时间长短与模型的复杂性、计算机性能等因素有关。

最后，进行后处理。

在有限元分析中，后处理是对求解结果的分析和可视化。

UG提供了丰富的后处理工具，可以对应力、应变等结果进行图形显示和数据分析，并以形式化报告的形式输出结果。

总结而言，UG有限元分析是一项强大的工程分析工具，可以帮助工程师解决各种复杂的力学问题。

通过建立几何模型、网格划分、定义边界条件和加载条件、求解和后处理，可以得到模型的应力、应变等结果，以指导后续的工程设计和优化工作。

UG有限元分析步骤精选整理.doc
1. 准备模型：首先，在UG中绘制需要分析的零件或装配体的3D模型。

确保模型的几何尺寸和材料等参数设置正确。

2. 网格划分：将模型分割成许多小单元，称为网格单元。

这些单元的大小和形状应
该足够小和简单，以便于计算程序的处理。

3. 材料属性定义：为每个网格单元定义材料性质。

这些属性包括弹性模量、泊松比、密度等。

4. 约束条件设置：定义所有约束条件，如边界约束、支撑条件等。

这些条件对应于
被分析部件的实际使用场景。

5. 载荷应用：将载荷应用于模型。

这些载荷可以是静态或动态载荷、温度载荷等，
也可以模拟外部力或压力。

6. 求解模型：选定求解器，使用许多数学方法解决数学方程，以有效地计算应力、
应变和变形等设计参数。

7. 结果分析：对有限元分析的各个方面进行评估和评估，检查计算的准确性和可靠性。

这些结果可以用于优化设计，以改进零件或装配体的性能。

8. 优化设计：如果有必要，使用有限元分析的结果来重新设计零件或装配体，并在
再次进行分析前进行修改。

总之，UG有限元分析是一种重要的工具，用于设计和生产过程中的性能优化和验证。

这个步骤需要正确的建模和分析，以确保计算是精确和可靠的。

UG有限元分析教程有限元分析（Finite Element Analysis，简称FEA）是一种工程设计和数值计算的方法，通过将复杂结构分割为许多简单的有限元单元，然后通过建立有限元模型，进行数值计算，最终得到结构的力学响应。

本文将向大家介绍UG有限元分析教程。

UG是一种集成的CAD/CAM/CAE软件，具有功能强大且广泛应用的特点。

UG有限元分析是UG软件中的一个功能模块，它可用于进行各种结构的有限元分析，例如静态分析、动态分析、热传导分析等。

2.有限元网格划分：将结构几何模型划分为许多有限元单元，每个单元由节点和单元单元构成。

UG提供了自动网格划分工具，用户可以选择合适的网格密度和单元类型。

3.材料属性定义：为结构的各个部分定义材料属性，包括杨氏模量、泊松比、密度等。

用户可以根据实际情况选择合适的材料模型。

4.边界条件和加载：为结构的边界和加载部分定义边界条件和加载，包括支撑约束、力、压力等。

用户可以根据实际情况选择合适的加载方式。

5.求解：通过对有限元模型进行离散化和求解，得到结构的力学响应。

UG提供了高效的求解器和迭代算法，可以快速求解大规模的有限元模型。

6.结果后处理：对求解结果进行后处理，包括位移、应力、应变等的分析和可视化。

UG提供了丰富的后处理工具，用户可以生成各种工程报表和图形。

UG有限元分析教程提供了详细的步骤和示例，帮助用户快速学习和掌握UG有限元分析的基本方法和技巧。

课程内容包括UG软件的基本操作、几何建模、有限元网格划分、材料属性定义、边界条件和加载的设定、求解器和后处理工具的使用等。

学习UG有限元分析需要一定的工程基础和计算机技巧，但是通过系统的学习和实践，任何人都可以掌握这一方法，并在工程设计和研究中应用它。

总之，UG有限元分析教程提供了全面的学习资料和实例，帮助用户了解和掌握UG有限元分析的基本理论和应用方法，为工程设计和研究提供了有力的工具和支持。

第1章 有限元分析方法及NX Nastran 的由来专业文档供参考，如有帮助请下载。

0 UG 有限元分析第1章 有限元分析方法及NX Nastran 的由来1.1 有限元分析方法介绍计算机软硬件技术的迅猛发展，给工程分析、科学研究以至人类社会带来急剧的革命性变化，数值模拟即为这一技术革命在工程分析、设计和科学研究中的具体表现。

数值模拟技术通过汲取当今计算数学、力学、计算机图形学和计算机硬件发展的最新成果，根据不同行业的需求，不断扩充、更新和完善。

1.1.1 有限单元法的形成近三十年来，计算机计算能力的飞速提高和数值计算技术的长足进步，诞生了商业化的有限元数值分析软件，并发展成为一门专门的学科——计算机辅助工程CAE （Computer Aided Engineering ）。

这些商品化的CAE 软件具有越来越人性化的操作界面和易用性，使得这一工具的使用者由学校或研究所的专业人员逐步扩展到企业的产品设计人员或分析人员，CAE 在各个工业领域的应用也得到不断普及并逐步向纵深发展，CAE 工程仿真在工业设计中的作用变得日益重要。

许多行业中已经将CAE 分析方法和计算要求设置在产品研发流程中，作为产品上市前必不可少的环节。

CAE 仿真在产品开发、研制与设计及科学研究中已显示出明显的优越性：❑ CAE 仿真可有效缩短新产品的开发研究周期。

❑ 虚拟样机的引入减少了实物样机的试验次数。

❑ 大幅度地降低产品研发成本。

❑ 在精确的分析结果指导下制造出高质量的产品。

❑ 能够快速对设计变更作出反应。

❑ 能充分和CAD 模型相结合并对不同类型的问题进行分析。

❑ 能够精确预测出产品的性能。

❑ 增加产品和工程的可靠性。

❑ 采用优化设计，降低材料的消耗或成本。

❑ 在产品制造或工程施工前预先发现潜在的问题。

❑ 模拟各种试验方案，减少试验时间和经费。

第1章 有限元分析方法及NX Nastran 的由来专业文档供参考，如有帮助请下载。

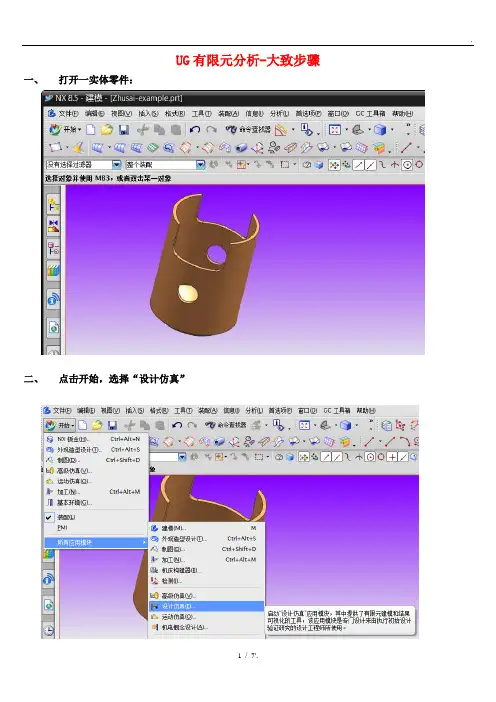
UG有限元分析-大致步骤一、打开一实体零件：
二、点击开始，选择“设计仿真”
三、点设计仿真后会自动跳出“新建FEM和仿真”窗口，点击“确定”
四、确定新建FEM和仿真后，会自动跳出“新建解决方案”窗口，点击“确定”
五、指派材料，点击零件，选择所需要指派的材料，点击“确定”，本例为steel
六、生成网格，以3D四面网格为例：选择网格-输入网格参数，单元大小
七、固定约束，选择所需要约束的面，本例的两个孔为固定约束
八、作用载荷，选择作用力的面，输入压力的大小，本例按单位面积的承压
九、求解，选择求解命令，点击确定
十、求解运算，系统会自动运算，显示作业已完成时，可以关闭监视器窗口
十一、导入求解结果，选择文件所在的路径，结果文件为 .op2, 点击确定十二、查看有限元分析结果：
十三、编辑注释，可以显示相关参数：
十四、动画播放，点击动画播放按键，可以设置动态播放速度的快慢。

UG有限元分析范文有限元分析（Finite Element Analysis，简称FEA）是一种力学分析方法，通过将连续物体的几何形状分割成有限数量的有限单元，再通过有限单元的力学行为对整个结构进行力学计算和应力分析。

有限元分析在工程设计、高科技制造、结构优化、材料研发等领域都有广泛应用。

有限元分析的基本过程是将问题的几何形状分割成有限数量的有限单元，并在每个单元上建立近似的解析解。

然后通过求解线性方程组，得到各个节点的位移、应力和应变等信息。

有限元分析的结果可以用来评估结构的强度、刚度、热传导、流体流动等性能，从而指导工程设计和优化。

有限元分析的主要步骤包括建立有限元模型、设定边界条件、施加荷载、求解方程和后处理结果。

建立有限元模型时，需要选择适当的有限元单元类型和网格划分方式，以便准确描述物体的几何形状和特性。

设定边界条件是指对有限元模型的边界进行约束，例如固支条件、周期边界条件和接触条件等。

施加荷载是指在有限元模型上施加外部力或位移条件，模拟实际工况。

求解方程通常使用数值方法，如有限差分法或迭代法，计算出线性方程组的解。

最后，根据求解得到的结果，可以进行应力分析、刚度分析和模态分析等，以评估结构的性能和安全性。

有限元分析的优点是能够描述复杂几何形状和边界条件下的结构行为，能够以较小的代价进行预测和分析，为结构设计提供直观和可靠的工具。

然而，有限元分析也有其局限性，例如需要合理的网格划分和有限元模型的准确度依赖于对材料特性和边界条件的准确描述等。

在工程实践中，有限元分析常用于求解固体力学、流体力学、热传导和电磁场等领域的问题。

例如，在机械工程中，有限元分析可以用于评估零件的强度、刚度和疲劳寿命等，辅助设计优化。

在航空航天领域，有限元分析可以用于评估航空器的结构安全性和气动特性。

在建筑工程中，有限元分析可以用于评估建筑物的地震响应和结构稳定性等。

总之，有限元分析是一种重要的力学分析工具，通过将物体分割为离散的有限单元进行计算，可以解决各种工程问题。

第1章高级仿真入门在本章中，将学习：∙高级仿真的功能。

∙由高级仿真使用的文件。

∙使用高级仿真的基本工作流程。

∙创建FEM和仿真文件。

∙用在仿真导航器中的文件。

∙在高级仿真中有限元分析工作的流程。

1.1综述UG NX4高级仿真是一个综合性的有限元建模和结果可视化的产品，旨在满足设计工程师与分析师的需要。

高级仿真包括一整套前处理和后处理工具，并支持广泛的产品性能评估解法。

图1-1所示为一连杆分析实例。

图1-1连杆分析实例高级仿真提供对许多业界标准解算器的无缝、透明支持，这样的解算器包括NX Nastran、MSC Nastran、ANSYS和ABAQUS。

例如，如果结构仿真中创建网格或解法，则指定将要用于解算模型的解算器和要执行的分析类型。

本软件使用该解算器的术语或“语言”及分析类型来展示所有网格划分、边界条件和解法选项。

另外，还可以求解模型并直接在高级仿真中查看结果，不必首先导出解算器文件或导入结果。

高级仿真提供基本设计仿真中需要的所有功能，并支持高级分析流程的众多其他功能。

∙高级仿真的数据结构很有特色，例如具有独立的仿真文件和FEM文件，这有利于在分布式工作环境中开发有限元（FE）模型。

这些数据结构还允许分析师轻松地共享FE数据去执行多种类型分析。

UG NX4高级仿真培训教程2∙高级仿真提供世界级的网格划分功能。

本软件旨在使用经济的单元计数来产生高质量网格。

结构仿真支持完整的单元类型（1D、2D和3D）。

另外，结构级仿真使分析师能够控制特定网格公差。

例如，这些公差控制着软件如何对复杂几何体（例如圆角）划分网格。

∙高级仿真包括许多几何体简化工具，使分析师能够根据其分析需要来量身定制CAD几何体。

例如，分析师可以使用这些工具提高其网格的整体质量，方法是消除有问题的几何体（例如微小的边）。

∙高级仿真中专门包含有新的NX传热解算器和NX流体解算器。

NX传热解算器是一种完全集成的有限差分解算器。

它允许热工程师预测承受热载荷系统中的热流和温度。

UG有限元分析范文有限元分析（Finite Element Analysis，简称FEA）是一种用数值方法解决工程问题的技术。

它将复杂的实际结构分割成许多小的有限元，通过计算每个有限元的行为，然后将这些行为合并起来得出整体结构的行为。

有限元分析广泛应用于机械、土木、航空、汽车等领域，可以对结构的应力分布、变形特性、热传导等进行分析和预测。

有限元分析的基本原理是将连续体划分为若干个由节点和单元组成的有限元网格。

每个有限元通过节点与相邻的有限元相连，形成整个结构的网格系统。

通过对每个有限元进行力学方程求解，可以得到整个结构的力学响应。

有限元分析的主要步骤包括建模、网格划分、边界条件设定、材料参数设定、求解和后处理等。

建模是有限元分析的第一步，将实际结构抽象成一个数学模型。

建模过程需要考虑结构的几何形状、材料性质、加载条件等。

根据实际情况，可以选择使用二维或三维模型。

网格划分是将结构划分为若干个有限元的过程。

有限元的划分方式有很多种，可以根据实际情况选择合适的划分方式。

在划分网格时，需要考虑到结构的几何形状和实际要求，保证网格的质量和密度。

边界条件设定是指在解算过程中，为了确定结构的运动状态，在有限元模型的边界上设定一些已知的位移、载荷或约束条件。

根据实际情况，可以设定结构的固支、自由度、外载荷等。

材料参数设定是指确定结构中各个部分的材料性质。

不同材料具有不同的弹性、热传导、热膨胀等性质，为了得到准确的分析结果，需要正确地设置材料参数。

求解是将有限元模型转化为一个数学问题，并通过数值计算方法求解。

求解过程中，需要根据结构的边界条件和材料参数，构造合适的数学模型，利用数值计算方法求解出结构的位移、变形、应力等。

后处理是指对求解结果进行分析和评估。

通过后处理可以获得结构各个部分的应力分布、变形特性、位移响应等。

后处理结果可以用于结构的优化设计和安全评估。

总之，有限元分析是一种重要的工程分析方法，可以帮助工程师对复杂的结构进行分析和预测。

UG有限元分析-大致步骤一、打开一实体零件：
二、点击开始，选择“设计仿真”
三、点设计仿真后会自动跳出“新建FEM和仿真”窗口，点击“确定”
四、确定新建FEM和仿真后，会自动跳出“新建解决方案”窗口，点击“确定”
五、指派材料，点击零件，选择所需要指派的材料，点击“确定”，本例为steel
六、生成网格，以3D四面网格为例：选择网格-输入网格参数，单元大小
七、固定约束，选择所需要约束的面，本例的两个孔为固定约束
八、作用载荷，选择作用力的面，输入压力的大小，本例按单位面积的承压
九、求解，选择求解命令，点击确定
十、求解运算，系统会自动运算，显示作业已完成时，可以关闭监视器窗口
十一、导入求解结果，选择文件所在的路径，结果文件为 .op2, 点击确定
十二、
十三、
十四、
十五、查看有限元分析结果：
十六、
十七、编辑注释，可以显示相关参数：
十八、
十九、
二十二、动画播放，点击动画播放按键，可以设置动态播放速度的快慢。

UG有限元分析第8章第8章中，我们将讨论有限元分析的几个关键方面，包括网格划分、单元类型、节点和边界条件以及有限元方程的求解方法。

首先，网格划分是有限元分析中最关键的步骤之一、网格划分决定了模型的精度和计算效率。

通常，我们将模型划分为多个小的几何单元，比如三角形或四边形。

划分方法有很多种，包括传统方法、自适应方法和网格生成软件等。

选择适当的划分方法可以提高模型的计算精度和稳定性。

接下来，我们将讨论几种常见的单元类型。

常见的单元包括线性单元、二次单元、三角形单元和四边形单元等。

每种单元类型各有优点和适用范围，我们需要根据具体问题选择合适的单元类型。

同时，我们还可以通过组装不同形状和尺寸的单元来构建复杂的几何模型。

节点和边界条件是有限元分析中另一个重要的方面。

节点是模型中特定位置的数学表示，边界条件描述了模型的边界上的约束和加载。

在有限元分析中，我们需要根据实际问题选取合适的节点，并设置相应的边界条件。

节点和边界条件的选择将直接影响到模型的计算结果。

最后，我们将介绍一些常见的有限元方程的求解方法。

有限元方程通常是一个大型的线性方程组，包含大量的未知数和约束条件。

为了求解这个方程组，我们可以使用直接方法或迭代方法。

直接方法包括高斯消元法、LU分解法和Cholesky分解法等，它们可以确切地求解方程组。

迭代方法包括雅可比迭代法、高斯-赛德尔迭代法和共轭梯度法等，它们通过迭代逼近来求解方程组。

选择合适的求解方法可以提高计算效率和准确性。

综上所述，有限元分析的第8章包括了网格划分、单元类型、节点和边界条件以及有限元方程的求解方法等关键方面。

这些内容对于理解和应用有限元分析技术都具有重要的意义。

掌握这些知识可以帮助我们更好地理解和使用有限元分析方法来解决实际工程问题。

㄀1ゴ催㑻ӓⳳ 䮼ゴЁˈ д˖x催㑻ӓⳳⱘ 㛑DŽx⬅催㑻ӓⳳՓ⫼ⱘ ӊDŽxՓ⫼催㑻ӓⳳⱘ ԰⌕⿟DŽx FEM ӓⳳ ӊDŽx⫼ ӓⳳ 㟾 Ёⱘ ӊDŽx 催㑻ӓⳳЁ 䰤 ԰ⱘ⌕⿟DŽ1.1㓐䗄UG NX4催㑻ӓⳳ ϔϾ㓐 ⱘ 䰤 ῵ 㒧 㾚 ⱘѻ ˈ ⒵䎇䆒䅵 ⿟ Ϣ ⱘ䳔㽕DŽ催㑻ӓⳳ ϔ ⧚ ⧚ ˈ ⊯ⱘѻ 㛑䆘Ԅ㾷⊩DŽ 1-1 ⼎Ўϔ䖲 ՟DŽ1-1䖲 ՟催㑻ӓⳳ կ 䆌 Ϯ⬠ 㾷ㅫ ⱘ 㓱ǃ䗣 ˈ䖭ḋⱘ㾷ㅫ NX NastranǃMSC NastranǃANSYS ABAQUSDŽ՟ ˈ 㒧 ӓⳳЁ 㔥Ḑ 㾷⊩ˈ 㽕⫼Ѣ㾷ㅫ῵ ⱘ㾷ㅫ 㽕 㸠ⱘ ㉏ DŽ 䕃ӊՓ⫼䆹㾷ㅫ ⱘ 䇁 Ā䇁㿔ā ㉏ ⼎ 㔥Ḑ ǃ䖍⬠ ӊ 㾷⊩䗝乍DŽ ˈ䖬 ҹ∖㾷῵ Ⳉ 催㑻ӓⳳЁ ⳟ㒧 ˈϡ 佪 㾷ㅫ ӊ 㒧 DŽ催㑻ӓⳳ կ 䆒䅵ӓⳳЁ䳔㽕ⱘ 㛑ˈ 催㑻 ⌕⿟ⱘӫ Ҫ 㛑DŽx催㑻ӓⳳⱘ 㒧 ⡍㡆ˈ՟ ⣀ゟⱘӓⳳ ӊ FEM ӊˈ䖭 Ѣ ԰⦃ Ё 䰤 ˄FE˅῵ DŽ䖭ѯ 㒧 䖬 䆌 䕏ѿFE 㸠 ⾡㉏ DŽUG NX4催㑻ӓⳳ 䆁 ⿟2x催㑻ӓⳳ կϪ⬠㑻ⱘ㔥Ḑ 㛑DŽ 䕃ӊ Փ⫼㒣⌢ⱘ 䅵 ѻ⫳催䋼䞣㔥ḐDŽ㒧 ӓⳳ ⱘ ㉏ ˄1Dǃ2D 3D˅DŽ ˈ㒧 㑻ӓⳳՓ 㛑 ⡍ 㔥Ḑ DŽ՟ ˈ䖭ѯ ⴔ䕃ӊ ԩ ԩԧ˄՟ 㾦˅ 㔥ḐDŽx催㑻ӓⳳ 䆌 ԩԧㅔ ˈՓ 㛑 ḍ 䳔㽕 䞣䑿 CAD ԩԧDŽ՟ ˈ ҹՓ⫼䖭ѯ 催 㔥Ḑⱘ ԧ䋼䞣ˈ ⊩ ⍜䰸 䯂乬ⱘ ԩԧ˄՟ ⱘ䖍˅DŽx催㑻ӓⳳЁϧ䮼 ⱘNXӴ⛁㾷ㅫ NX⌕ԧ㾷ㅫ DŽ¾NXӴ⛁㾷ㅫ ϔ⾡ 䲚 ⱘ 䰤 㾷ㅫ DŽ 䆌⛁ ⿟ 乘⌟ ⛁䕑㥋㋏㒳Ёⱘ⛁⌕ ⏽ DŽ¾NX⌕ԧ㾷ㅫ ϔ⾡䅵ㅫ⌕ԧ ˄CFD˅㾷ㅫ DŽ 䆌 㸠〇 ǃϡ 㓽ⱘ⌕ ˈ ㋏㒳Ёⱘ⌕ԧ䖤 乘⌟⌕⥛ ẃ ˈгҹՓ⫼NXӴ⛁ NX⌕ԧϔ䍋 㸠㗺 Ӵ⛁/⌕ԧ DŽ1.2ӓⳳ ӊ㒧䗮䖛催㑻ӓⳳ ԰⌕ ˈ ⫼4Ͼ ⾏ 㘨ⱘ ӊ DŽ㽕 催㑻ӓⳳЁ催 ԰ˈ䳔㽕њ㾷 ѯ Ͼ ӊЁˈҹ 䙷ѯ Ͼ ӊ 乏 ▔⌏ⱘ ԰䚼ӊDŽ䖭4Ͼ ӊ 㸠Ѣӓⳳ䖛⿟ˈ 1-2 ⼎DŽ1-2ӓⳳ ӊ㒧ℷ㹿 ⱘ 䆒䅵䚼ӊϔϾ .prt ⱘ䚼ӊ ӊDŽ՟ ˈϔϾ ҹ㹿 Ўplate.prtⱘ䚼ӊDŽ䚼ӊ ӊ Џ῵ 䚼ӊ ϔ㺙䜡ˈ ϔϾ ⱘ䚼ӊ ԩԧDŽ⫼ϔϾ⬅ ҪҎ䆒䅵ⱘ῵ ˈ 㛑≵ ⱘ 㡄DŽ 䖛⿟ ˈ䗮 Џ῵ 䚼ӊ ӊ ϡ㹿 ⱘDŽ䆒䅵䚼ӊ ӊⱘ⧚ϔϾ⧚ 䚼ӊ ӊ㹿 ゟ ˈ咬䅸 ϔ.prt ˈfem#_i 䚼ӊ ⱘ䰘 DŽ՟ ˈ 䚼ӊ plate.prtˈϔϾ⧚ 䚼ӊ㹿 Ўplate_fem1_i.prtDŽϔϾ⧚ 䚼ӊ 䆒䅵䚼ӊⱘϔϾⳌ ˈ ҹ DŽ⧚ 䅽⫼ ⫼⧚ 䚼ӊ Џ῵ ⱘ䆒䅵⡍ DŽϡ Џ῵ 䚼ӊˈ㄀1ゴ催㑻ӓⳳ 䮼3㗠 䳔㽕 ⧚ 䚼ӊϞ 㸠 ԩԧ⧚ DŽ՟ ˈ ҹ⿏ ⡍ ˈ Ё㹿 ⬹ⱘ ⱘ ԩ㒚㡖DŽϔ 䆒䅵䚼ӊ ӊⱘϡ ㉏ ҹՓ⫼ Ͼ⧚ ӊDŽ䰤 ῵ ˄FEM˅ ӊゟϔFEM ӊ 咬䅸 ϔϾ.fem ˈ_fem# 䚼ӊ ⱘ䰘 DŽ՟ ˈ 䚼ӊ plate.prtˈϔϾFEM ӊ㹿 Ўplate_fem1.femDŽϔϾ 䰤 ῵ ӊ 㔥Ḑ˄㡖⚍Ϣ ˅ǃ⠽⧚⡍ DŽϔ ゟњ㔥Ḑˈ ҹ ⫼ㅔ ⿏ ҹ 㔥Ḑ 䋼䞣䆒䅵ЁⱘҎЎ 䈵ˈ 㒚䭓 䴶ǃ 䖍㓬 䚼 ӊDŽㅔ 䆌Ⳍ ϔ⡍ 䰤 䆒䅵 ⱘ㒚㡖㑻Ϟ㔥Ḑ ԩԧDŽԩԧ ⫳ ѢFEMЁⱘ 䖍 ԩԧϞˈ㗠ϡ ⧚ ⱘ Џ῵ ⱘ䚼ӊЁDŽϾFEM ӊ ҹ ⫼ ϔ⧚ 䚼ӊˈ ҹ ϡ ㉏ ϡ ⱘFEM ӊDŽӓⳳ ӊゟϔӓⳳ ӊ ˈ咬䅸ϔϾӓⳳ ӊ ϔ.sim ˈ_sim# 䚼ӊ ⱘ䰘 DŽ՟ ˈ 䚼ӊ plate.prtˈϔϾӓⳳ ӊ㹿 Ўplate_sim1.simDŽӓⳳ ӊ ӓⳳ ˈ 㾷ㄨǃ㾷ㅫ䆒㕂ǃ䕑㥋ǃ㑺 ǃ Ⳍ ⱘ ǃ⠽⧚⡍ ˈ ҹ ӊ ゟ䆌 㘨 ϔFEMⱘӓⳳ ӊDŽ㸠 Ͼ ㉏ ˈ4Ͼ ⾏ⱘ ӊ կ♉⌏ DŽ 䆌 ˈ4Ͼ ӊ 䖲ⱘDŽ1.3催㑻ӓⳳ ԰⌕⿟ϔϾ ˈ 䆹 䆩 ∖㾷ⱘ䯂乬 ϔ њ㾷DŽ 䆹ⶹ䘧 ⫼ Ͼ∖㾷 ˈℷ 㸠ҔМ㉏ ⱘ 䳔㽕ҔМ㉏ ⱘ㾷 ḜDŽϟ ㅔ㽕 њ 㒧 ӓⳳЁ䗮⫼ⱘ ԰⌕⿟DŽ˄1˅ NXЁˈ ϔ䚼ӊ ӊDŽ˄2˅ 催㑻ӓⳳ ⫼DŽЎFEM ӓⳳ ӊ㾘 咬䅸∖㾷 ˄䆒㕂⦃ ˈ 䇁㿔˅DŽ⊼ ˖ FEM ē d˄3˅ ゟϔ㾷 ḜDŽ䗝 ∖㾷 ˄ NX Nastran˅ǃ ㉏ ˄ Structural˅ 㾷 Ḝ㉏ ˄ Linear Statics˅DŽ˄4˅ 䳔㽕ˈ⧚ 䚼ӊ ԩԧDŽϔ Փ⧚ 䚼ӊ▔⌏ˈ ҹ⿏ ϡ䳔㽕ⱘ㒚㡖ˈ 㾦ˈ 䱨 ԩԧ ԧ㔥Ḑ ゟЁ䴶DŽ˄5˅ՓFEM ӊ▔⌏ˈ㔥Ḑ ԩԧDŽ佪 ⫼㋏㒳咬䅸㞾 㔥Ḑ ԩԧDŽ 䆌 ϟ㋏㒳咬䅸 կϔ ⱘ催䋼䞣ⱘ㔥Ḑˈ 乏 Փ⫼DŽUG NX4催㑻ӓⳳ 䆁 ⿟4˄6˅Ẕ 㔥Ḑ䋼䞣DŽ 䳔㽕ˈ ҹ⫼䖯ϔℹ⧚ 䚼ӊ ԩԧ㒚 㔥Ḑˈℸ FEMЁ ҹ ⫼ㅔ ˈ⍜䰸 㔥Ḑ ῵ ⬅CAD ԩԧ 㛑 䍋ⱘϡ 㒧 ⱘ䯂乬DŽ˄7˅ ⫼ϔ 㔥ḐDŽ˄8˅ 㔥Ḑ⒵ ˈՓӓⳳ ӊ▔⌏ǃ԰⫼䕑㥋Ϣ㑺 ῵ DŽ˄9˅∖㾷῵ DŽ˄10˅ ⧚Ё㗗 㒧 DŽ1.4ӓⳳ 㟾ӓⳳ 㟾 ˄Simulation Navigator˅ կ ϔ ⢊㒧 ЁˈϔϾ㾖 㒉ϔCAE ⱘϡ ӊ 㒘 ⱘ ⊩DŽ↣ϔϾ ӊ 㒘 㹿 ⼎Ў Ёⱘϔ ⾏㡖⚍ˈ 1-3 ⼎DŽӓⳳ 㟾 Ё կњⳈ Ⳉ䗮 㦰 DŽ ҹ ӓⳳ 㟾 ЁⳈ 㸠 ԰ˈҷ Փ⫼ ҸDŽ՟ ˈ ゟϔ ⱘ∖㾷 Нˈ ҹ 䕑㥋 㑺 Ңϔ ӓⳳ 㟾 ⱘ ϔϾЁDŽ1-3ӓⳳ 㟾㄀1ゴ催㑻ӓⳳ 䮼5 1.4.1ⳳ 㡖觥閅蹉缬譄訝詢ӓⳳ 㟾 ⱘ乊䚼䴶 ⼎ ӊⱘ DŽ 1-4 ⼎Ў ϔϾ乊㑻ӓⳳ ӊ ⱘ ՟ DŽ䗝Ё 䗝Ḛ ҹ 乍Ⳃⱘ ⼎DŽ1-4ӓⳳ 㟾 Ёⱘ ⾡㡖⚍㸼1-1 ⼎ⱘ ӓⳳ 㟾 Ё ⾡㡖⚍ⱘ催㑻㓐䗄DŽ㸼1-1ӓⳳ 㟾 㡖⚍ 䗄㡖⚍ 㡖⚍ 䗄ӓⳳ ӓⳳ ˈ ϧ䮼∖㾷 ǃ㾷 Ḝǃ㾷 Ḝ䆒㕂ǃӓⳳ 䈵ǃ䕑㥋ǃ㑺 DŽ ҹ Ͼӓⳳ ӊϢϔ ϾFEM ӊ 㘨FEM 㔥Ḑ ǃ⠽⧚⡍ ǃ 䖍 ԩԧDŽFEM ӊ Ⳍ ⧚ DŽ ҹ 㘨 ϾFEM ӊ ϔ Ͼ⧚ 䚼ӊ⧚ 䚼ӊ ⧚ 䚼ӊˈ ゟϔFEM ⬅䕃ӊ㞾 ゟЏ῵ 䚼ӊ Џ῵ 䚼ӊ ԰䚼ӊ ˈ Џ῵ 䚼ӊ㡖⚍Ϟ ゟϔ ⱘFEM ⼎ ⱘ⧚ 䚼ӊ䖍 ԩԧ 䖍 ԩԧ˄ 䖍 ԧǃ㸼䴶 䖍㓬˅DŽϔ 㔥Ḑ 䰤 ῵ ˈӏԩ䖯ϔℹ ԩԧ ⫳ 䖍 ԩԧϞˈ㗠ϡ ⧚ Џ῵ 䚼ӊϞUG NX4催㑻ӓⳳ 䆁 ⿟6㓁㸼 㡖⚍ 㡖⚍ 䗄0D㔥Ḑ 䳊㓈˄0D˅㔥Ḑ1D㔥Ḑ ϔ㓈˄1D˅㔥Ḑ2D㔥Ḑ Ѡ㓈˄2D˅㔥Ḑ3D㔥Ḑ ϝ㓈˄3D˅㔥Ḑӓⳳ 䈵 㾷ㅫ 㾷 Ḝϧ ⱘ 䈵ˈ 㞾 䇗⏽ ǃ㸼Ḑ ⌕ 㸼䴶䕑㥋 ӓⳳ ӊⱘ䕑㥋DŽ ϔ㾷 Ḝ ˈ䕑㥋 ˄Load Container˅ 㒭ӊ ⱘ䕑㥋㑺 ӓⳳ ӊⱘ㑺 DŽ ϔ㾷 Ḝ ˈ㑺 ˄Constraint Container˅ 㾷 Ḝⱘ㑺㾷 Ḝ 㾷 Ḝ 䈵ǃ䕑㥋ǃ㑺 㾷 Ḝⱘℹ ϔ㾷 Ḝ ↣ϔϾ 㾷 Ḝⱘ ԧˈ 䕑㥋ǃ㑺 ӓⳳ 䈵㒧 Ңϔ∖㾷 ⱘӏϔ㒧 DŽ 㕂 ⧚ Ёˈ ҹ 㒧 㡖⚍ˈ ⫼ ӓⳳ 㟾 ⱘ 㾕 䗝Ḛ ⾡㒧 㒘ⱘ ⼎1.4.2ⳳ㾚閅芉絓ӓⳳ ӊ㾚 ϔϾ⡍⅞⌣㾜 に ˈ Ѣӓⳳ 㟾 ЁDŽ䆹に ˖x ⼎ 䕑ⱘ䚼ӊˈҹ 䖭ѯ䚼ӊ Џ῵ 䚼ӊ ⃵ ㋏Ёⱘ FEM ӓⳳ ӊDŽx 䆌䕏 ⼎ⱘ䚼ӊˈ ⊩ 㽕 ⼎ⱘ䚼ӊDŽ¾ ϔ ԧℷ ⼎ˈ ⼎Ў 㡆ˈϨ ⿄Ӯ催҂ ⼎DŽ¾ ϔ ԧϡ ⼎ˈ ♄DŽx 䆌 ӏԩ䆒䅵 ⧚ 䚼ӊϞ ⱘFEM ӓⳳ ӊˈ㗠ϡ 佪 ⼎䚼ӊDŽӓⳳ ӊ㾚 1-5 ⼎DŽ㄀1ゴ催㑻ӓⳳ 䮼71-5ӓⳳ ӊ㾚1.5㒗д㒗дЁ ⫼ϔϝ㓈 ԧ㔥Ḑˈ ϔϾ䖲 䚼ӊˈњ㾷催㑻ӓⳳ ԰⌕⿟ˈ д˖x 䚼ӊ ゟFEM ӓⳳ ӊDŽx 㔥Ḑ ⧚ ԩԧDŽx㔥Ḑ 䚼ӊDŽxЎ㔥Ḑ Нϔ DŽx԰⫼䕑㥋 㑺 䚼ӊDŽx∖㾷῵ DŽx㾖 㒧 DŽ㄀1ℹ 䚼ӊˈ 催㑻ӓⳳx NXЁˈ rod.prt䚼ӊˈ 1-6 ⼎DŽx Advanced Simulation ⫼DŽ䗝 StartėAll ApplicationsėAdvanced SimulationDŽx 䌘⑤ Ϟˈ Simulation Navigator DŽx 䫔˄pin˅ ӓⳳ 㟾 DŽx ӓⳳ 㟾 Ёˈ rod.prt 䗝 New FEM and SimulationDŽ1-7 ⼎ˈNew FEM and Simulation 䆱Ḛ 3Ͼ 㞾 ゟⱘ ӊDŽDefaultUG NX4催㑻ӓⳳ 䆁 ⿟8LanguageϟNX NASTRANЎ∖㾷 ˈAnalysis Type䗝 StructuralDŽ1-6rod.prt 1-7New FEM and Simulation 䆱Ḛx New FEM and Simulation 䆱ḚЁⱘOK 䪂DŽ⦄Create Solution 䆱Ḛˈ 1-8 ⼎ˈ咬䅸Solver NX NASTRANDŽx Create Solution 䆱ḚЁⱘOK 䪂DŽSimulation Navigator ⼎Simulation FEM ӊˈ 1-9 ⼎DŽ1-8Create Solution 䆱Ḛ 1-9ӓⳳ 㟾 ㄀2ℹ⧚ ԩԧℸ㒗дˈ ѯ䆒䅵⡍ ҹҢ䚼ӊ⿏ ˈ Ў Ӏ ϡ䞡㽕ⱘDŽx Simulation NavigatorЁˈ Simulation File View 㹿 ˈ Simulation File㄀1ゴ催㑻ӓⳳ 䮼9View DŽx rod_fem1_iDŽ⼎˖ ē ω Make Displayed PartDŽ⧚ ⱘ䚼ӊ⦄ ӓⳳ 㟾 Ё㹿▔⌏DŽx Advanced Simulation Ёˈ Idealize Geometry DŽx䱣Idealize 䆱Ḛ ˈ䗝 䚼ӊDŽx䗝ЁHoles 䗝ḚDŽ⊼ ˖ Ӿ10ē ΄ ē ԉ 10mm d x OK 䪂DŽҢ⧚ 䚼ӊ㹿⿏ ˈ 1-10 ⼎DŽ1-10⧚ 䚼ӊx Save ˈ ▔⌏ⱘ ӊDŽ㄀3ℹ 䚼ӊ㔥ḐЎњ 䚼ӊ㔥Ḑˈ佪 䳔㽕ՓFEM ӊ▔⌏DŽx Simulation File ViewЁˈ rod_fem1DŽFEM ӊ㹿▔⌏ ӓⳳ 㟾 ⱘ乊䚼DŽx Advanced Simulation Ϟˈ 3DTetrahedral Mesh DŽ⼎˖ Ҷ ӽ rod_fem1ω New Meshė3D Tetrahedralēdx䱣3D Mesh 䆱Ḛ ˈ䗝 ԧDŽxҢType 㸼䗝 CTETRA˄10˅ DŽ⊼ ˖CTETRAď10Đ CTETRAď4Đ NASTRANӦ dx Overall Element SizeḚЁ 4.0DŽx OK 䪂 ゟ㔥Ḑˈ 1-11 ⼎DŽ1-12 ⼎ˈ3D㔥Ḑ㹿 Simulation NavigatorЁDŽUG NX4催㑻ӓⳳ 䆁 ⿟101-11㔥Ḑ 䚼ӊ 1-12㔥Ḑ㡖⚍x Save ˈ FEM ӊDŽ㄀4ℹЎ㔥Ḑ Нϔx Advanced Simulation Ϟˈ Material Properties DŽ⼎˖ ToolsėMaterial Properties dx Materials 䆱ḚЁˈ Library DŽx Search Criteria 䆱ḚЁˈ OK 䪂DŽx Search Result 䆱ḚЁˈ䗝 ЎSteelⱘ ˈ✊ OK 䪂DŽ⡍ 㹿 䕑 Materials 䆱ḚЁDŽ԰⫼ 㔥ḐDŽxՓ Materials 䆱ḚЁⱘSTEEL㹿҂ DŽx Simulation NavigatorЁˈ ˄䗝 ˅3d_mesh˄1˅䗝 㔥ḐDŽx 䆱ḚЁˈ OK 䪂DŽ㹿䖲 㔥ḐDŽ ⫼Simulation NavigatorˈẔ 㹿԰⫼ 㔥ḐDŽx Simulation Navigator 䆱ḚЁˈ 3d_mesh˄1˅ 䗝 Edit AttributesDŽx Element Attributes 䆱ḚЁˈẔ STEEL㹿 Ў԰⫼ 㔥Ḑⱘ DŽx Cancel 䪂DŽx ӊDŽ㄀5ℹ԰⫼ϔ䕈 䕑㥋x Simulation File Viewに Ёˈ rod_sim1DŽ ӓⳳ 㟾 ЁՓSimulation ӊ▔⌏DŽ㔥Ḑ ⼎ˈ 㗠 䴶䗝 DŽx Simulation NavigatorЁϡ䗝Ё3d_mesh˄1˅ 䗝Ḛˈ 1-13 ⼎DŽx Advanced Simulation Ϟˈ Load Type Ёⱘㆁ ˈ✊ Bearing DŽ㄀1ゴ催㑻ӓⳳ 䮼111-13 3D㔥Ḑ ⼎⊼ ˖ Simulation Navigatorē ԅ ̣ďSolution1Đ ē Loadsēω New LoadėBearing d䕈 䕑㥋㽕∖㾘 ϔ 㸼䴶˄ 䖍㓬˅ˈ ϔ㾘 䕑㥋 ⱘⶶ䞣DŽ佪 ˈ䗝 ԩԧüü䕈 䕑㥋 ԰⫼ⱘ 䴶DŽx Create Bearing 䆱Ḛˈ䗝 䚼ӊ ッⱘ 䴶ˈ 1-14 ⼎DŽ1-14䗝 䕑㥋԰⫼㸼䴶x Force ḚЁ䕧 1000DŽ⊼ ˖ ďRegion AngleĐ Ӿ180d Ӿ б 180e d⃵ˈ䗝 㽕 Нⱘ 䕑㥋ⱘⶶ䞣 DŽx Inferred Vector Ёⱘㆁ ˈ –YC Axis DŽx OK 䪂DŽ䕑㥋 ゟ ⼎ Ёˈ 1-15 ⼎DŽ䕑㥋Ϟ ⼎ⱘㆁ ϔbitˈ ⫼BC Edit Display 䆱Ḛ 䖍⬠ ӊⱘ 䉠DŽx Simulation NavigatorЁ Solution˄1˅ϟⱘBearing˄1˅䕑㥋ˈ✊ 䗝 StyleDŽx BC Edit Display 䆱ḚЁˈ ⿏ Scale⒥ ㆁ ˈ✊ OK 䪂DŽㆁ ˈ 1-16 ⼎DŽUG NX4催㑻ӓⳳ 䆁 ⿟121-15 ゟ ⼎䕑㥋 1-16 ⱘ䕑㥋 ⼎㄀6ℹ԰⫼㄀ϔ㑺⫼ϔ䫔ԣ㑺 ˈ ⱘϔッ㑺 ⱘ 䴶DŽ䆹㑺 ӓⳳℸ䴶 ḋϢ ϔ䚼ӊϞⱘ 䴶 䜡DŽϔϾ䫔ԣ㑺 Нϔ 䕀䕈DŽϔ 䗝 њϔ 䴶ˈ ゟϔ ㋏ˈR Z 㹿 ˈTheta˄ 䕀˅ 㞾⬅ⱘDŽx Advanced Simulation Ϟˈ Constraint Type Ёⱘㆁ ˈ✊ Pinned Constraint DŽ⊼ ˖ Simulation Navigatorē ԅ ̣ďSolution1Đ Constraints ω New ConstraintėPinned Constraint dx Create Pinned Constraint 䆱Ḛˈ䗝 䖲 䚼ⱘ 䴶ˈ 1-17 ⼎DŽx OK 䪂DŽ㑺 㹿԰⫼ⱘ ⼎DŽ⬅㑺 ゟⱘ ㋏г 㾕ⱘˈ 1-18 ⼎DŽ1-17䗝 䚼ⱘ 䴶 1-18 ゟϢ ⼎䫔ԣ㑺㄀1ゴ催㑻ӓⳳ 䮼13㄀7ℹ԰⫼㄀Ѡ㑺䚼ӊ 㹿㑺 ˈԚ㒩Z䕈ҡ✊ 㞾⬅ 䕀DŽ⦄ 䚼ӊ乊䚼 ϔ㑺 ˈ䰆ℶϔ ԧ䖤 DŽ ⫼⫼ Нⱘ㑺 ˈ ϔϾ㞾⬅ Ё㑺 ⚍DŽx Constraint Type Ёⱘㆁ ˈ✊ User Defined Constraint DŽx Create User Defined Constraint 䆱ḚЁⱘDOF1ḚЁˈ Fixed DŽx X ⿏㹿 ˈ ҪDOF 㞾⬅DŽx 䗝 ⚍˖ ῑⱘ乊ッ 䴶Ⳍ䘛ˈ 1-19 ⼎DŽx OK 䪂DŽゟ㑺 ˈ 1-20 ⼎DŽ1-19䗝 ⚍ 1-20 ゟϢ ⼎ 㑺x ӊDŽ㄀8ℹ∖㾷῵⦄ Нњ㔥Ḑǃ ǃ䕑㥋 㑺 ˈ ∖㾷῵ DŽ԰Ў䖛⿟ⱘϔ䚼 ˈ ⫼㓐 Ẕ ˈẔ偠῵ ↩DŽx Simulation NavigatorЁˈ Solution1 䗝 Comprehensive Checkˈ Informationに DŽx㗗 Ẕ 㒧 DŽẔ ⱘ 䄺 DŽxẔ 㤤䗝 Iterative Solver䗝乍ˈ ҹ 䖯 㛑DŽxẔ 䄺 ˖ 䫔ԣ㑺 ㋏ϡ Ѣ㡖⚍ϟⱘ ㋏DŽ ԰⫼䫔ԣ㑺 ˈ ⫼ϔ ㋏ 㡖⚍ϟⱘ ㋏DŽ䖭ϡӮ 䍋ӏԩ䯂乬ˈ ҹ ⬹䄺 DŽx 䯁Informationに DŽx Simulation NavigatorЁˈ Solution1ˈ 䗝 Solution AttributesDŽx Edit Solution 䆱ḚЁˈ䗝ЁIterative Solver˄ NX Nastran2.0 催⠜ ˅ 䗝ḚDŽx OK 䪂DŽx Simulation NavigatorЁˈ Solution1ˈ 䗝 SolveDŽUG NX4催㑻ӓⳳ 䆁 ⿟14⼎˖ Advanced Simulation Ӧ Solve γē Solveճ d Comprehensive Check dx OK 䪂DŽ⼎Informationに ˈ ⃵㓐 Ẕ DŽ䗮䖛Ẕ ˈ ⦄Analysis Job Monitor 䆱Ḛˈ ⼎ӏ ℷ 䖤㸠DŽ 䖤㸠ˈ ҹ ҹ㒻㓁⫼NX ԰ˈ㗠 䰤 ℷ 㹿䅵ㅫDŽx ӏ ˈ 䯁Informationに DŽx Analysis Job Monitor 䆱ḚϞ Cancel 䪂DŽ⦄ 㾷ㅫ ˈ 1-21 ⼎ˈResults㡖⚍ Simulation NavigatorЁ ҹ㾕 DŽ㄀9ℹ㾖 㒧⦄ ⫼ 㕂 ⧚ 㾖 㒧 DŽSimulation NavigatorЁˈ ResultsDŽ⼎˖ Ӧ Advanced Simulation ԅResults γd㒧 ⼎ 㕂 ⧚ に Ёˈ 1-22 ⼎DŽ1-21Results㡖⚍ 1-22㒧 ⼎ ⼎Post Control ˈ 1-23 ⼎DŽ1-23Post Control⼎˖ Post Control Ϣ ԅē Application ω Post Control d ㄀10ℹ ӓⳳ 㟾 Ё㗗 㒧䗮䖛ㅔ 䗝 㾘 䳔㽕ⱘ㉏ ˈ ҹ ⼎ⱘ㒧 ㉏ DŽ⊼ ˖咬䅸䗝 ԡ⿏㉏ DŽ䆌 㒧 ㉏ ϧ䮼ⱘ ㉏ ˄ 㒘 ˅DŽ 1-24ЁˈDisplacement 㒣 ҹ ⼎ϡ DŽ㄀1ゴ催㑻ӓⳳ 䮼151-24 ⱘԡ⿏㡖⚍x Simulation NavigatorЁˈ SUBCASE—STATIC LOADS1LoadsDŽx Displacement—NodalDŽx䗝ЁY㒘 䗝ḚDŽ⼎ ҹ ⼎Yԡ⿏ ˈ 1-25 ⼎DŽ1-25Yԡ⿏㄀11ℹ䗔 㕂 ⧚㾖 㒧 ˈ ҹ䗔 㕂 ⧚ DŽx Post Control Ϟˈ Finish Post Processing DŽ⼎˖ ToolsėResultsėFinish Post Processing dx 䯁 䚼ӊ ӊDŽ。

UG有限元分析学习引言：有限元分析是一种工程设计和分析方法，通过将复杂的结构分割成离散的有限元素，利用计算机进行数值计算和模拟，以分析和评估结构在受力和应变条件下的响应。

UG软件是目前工程领域广泛应用的有限元分析软件之一，本报告以UG有限元分析学习过程为主线，介绍学习过程、使用方法和应用案例。

一、学习过程在学习UG有限元分析之前，我通过阅读相关的教材和资料，了解了有限元分析的基本原理和方法。

然后，我开始学习UG软件的使用，包括安装、界面功能和基本操作等。

UG软件中的有限元分析模块可以在建模的同时进行，我通过学习建模技巧和参数设置来创建不同类型的结构模型。

在建模过程中，我还学会了对实体进行修剪和合并以及生成网格等操作。

接下来，我开始学习有限元分析的设置和求解。

UG软件提供了丰富的分析类型，包括静力学分析、动力学分析以及热力学分析等。

我通过学习分析类型的选择和参数设置等，掌握了有限元分析的实际应用技能。

二、使用方法在使用UG进行有限元分析时，我首先需要进行结构建模。

UG提供了多种建模方式，包括实体建模、曲面建模和体积建模等。

对于不同的结构类型，我可以选择合适的建模方式，并通过修剪、合并和倒角等操作进行构建。

建模完成后，我需要对结构进行网格划分。

UG软件提供了多种网格划分的算法和工具，我可以根据结构的特点和要求选择合适的划分方式。

同时，我还可以通过设置网格参数来控制划分质量和计算效果。

完成网格划分后，我需要进行边界条件和荷载的设置。

UG软件提供了丰富的边界条件和荷载类型供选择，我可以根据分析需要进行设置。

设置完成后，我就可以进行有限元分析的求解，UG软件会自动计算并给出分析结果。

三、应用案例我在学习过程中应用了UG有限元分析模块进行了几个实际案例的分析。

首先，我选择了一个简单的静态载荷下的梁的分析。

通过对梁的建模、网格划分、边界条件和荷载设置以及分析求解，我得出了梁的应力和位移分布，并通过对比理论计算结果验证了有限元分析的准确性。