贵阳专版2019届中考数学总复习第一部分教材知识梳理第7章圆第2节点直线与圆的位置关系精讲课件
- 格式:ppt
- 大小:4.50 MB
- 文档页数:29

第三节 正多边形与圆的有关计算贵阳中考考情预测贵阳近年真题试做正多边形与圆1.(2018·贵阳适考)如图,⊙O 的内接正六边形的面积为6 3 cm 2,则⊙O 的周长为( C )A .π cmB .2π cmC .4π cmD .8π cm2.(2016·贵阳中考)小颖同学在手工制作中,把一个边长为12 cm 的等边三角形纸片贴到一个圆形的纸片上,若三角形的三个顶点恰好都在这个圆上,则圆的半径为( B )A .2 3 cmB .4 3 cmC .6 3 cmD .8 3 cm圆的有关计算3.(2017·贵阳适考)如图,半圆O 的直径AB =20,将半圆O 绕点B 顺时针旋转30°得到半圆O′,与AB ︵交于点P.(1)求BP 的长;(2)求图中阴影部分的面积.(结果保留π)解:(1)连接AP.∵AB 为半圆O 的直径, ∴∠APB =90°. 在Rt △ABP 中,cos ∠ABP = cos 30°=BP AB,∴BP =103;(2)过点O 作OM⊥BP 于点M ,连接OP.在Rt △MOB 中,OB =12AB =10,∠ABA ′=30°,∴OM =12OB =5.∴MB =OB 2-OM 2=5 3. ∵OB =OP ,OM ⊥PB , ∴PM =MB =5 3. ∵∠ABP =30°, ∴∠AOP =2∠ABP=60°. ∴∠BOP =120°.∴S 阴影=S 半圆O′-(S 扇形POB -S △POB )=12π·102-⎝ ⎛⎭⎪⎫120·π·102360-12×103×5 =503π+25 3. ∴阴影部分的面积为503π+25 3.贵阳中考考点清单圆的弧长及扇形面积公式1.圆的半径是R ,弧所对的圆心角度数是n :正多边形与圆2.正多边形的边数为n ,外接圆半径为R :圆锥的侧面积与全面积底面的⑧中考典题精讲精练弧长计算例1 如图,在扇形OAB 中,∠AOB =60°,扇形半径为r ,点C 在AB ︵上,CD ⊥OA ,垂足为D ,当△OCD 的面积最大时,AC ︵的长为__14πr__.【解析】由OC =r ,点C 在AB ︵上,CD ⊥OA ,利用勾股定理可得DC 的长,求出OD =22r 时,△OCD 的面积最大,∠COA =45°时,利用弧长公式得到答案.1.(2018·遵义模拟)如图,⊙O 的半径为2,AB ,CD 是互相垂直的两条直径,点P 是⊙O 上任意一点(P 与A ,B ,C ,D 不重合),过点P 作PM⊥AB 于点M ,PN ⊥CD 于点N ,点Q 是MN 的中点,当点P 沿着圆周转过45°时,点Q 走过的路径长为( A )(第1题图)A .π4B .π2C .π6D .π3阴影部分面积计算例2 如图,在△ABC 中,BE 是它的角平分线,∠C =90°,D 在AB 边上,以DB 为直径的半圆O 经过点E ,交BC 于点F.(1)求证:AC 是⊙O 的切线;(2)已知 sin A =12,⊙O 的半径为4,求图中阴影部分的面积.【解析】(1)连接OE ,根据OB =OE ,得到∠OBE=∠OEB,再根据BE 是∠ABC 的平分线,得到∠OBE=∠EBC,由∠OBE=∠OEB,得到∠OEB =∠EBC ,从而判定OE∥BC,最后根据∠C =90°,得到∠AEO=∠C=90°,证得AC 是⊙O 的切线;(2)连接OF ,利用S 阴影=S 梯形OECF -S 扇形EOF ,求解即可.【答案】(1)证明:连接OE. ∵OB =OE ,∴∠OBE =∠OEB.∵BE 是△ABC 的角平分线,∴∠OBE =∠EBC. ∴∠OEB =∠EBC.∴OE∥BC. ∵∠C =90°,∴∠AEO =∠C=90°. ∴AC 是⊙O 的切线;(2)解:连接OF.∵sin A =12,∴∠A =30°.∵⊙O 的半径为4,∴AO =2OE =8. ∴AE =43,∠AOE =60°.∴AB =12. ∴BC =12AB =6,AC =6 3.∴CE =AC -AE =2 3.∵OB =OF ,∠ABC =60°,∴△OBF 是正三角形. ∴∠FOB =60°,CF =6-4=2. ∴∠EOF =60°.S 扇形EOF =360=3π.∴S 阴影=S 梯形OECF -S 扇形EOF =63-83π.2.(2018·安顺中考)如图,C 为半圆内一点,O 为圆心,直径AB 长为2 cm ,∠BOC =60°,∠BCO =90°,将△BOC 绕圆心O 逆时针旋转至△B′OC′,点C′在OA 上,则边BC 扫过区域(图中阴影部分)的面积为__π4__cm 2.(结果保留π)(第2题图)3.如图,AB 与⊙O 相切于点C ,OA ,OB 分别交⊙O 于点D ,E ,CD ︵=CE ︵. (1)求证:OA =OB ;(2)已知AB =43,OA =4,求阴影部分的面积.(1)证明:连接OC ,则OC⊥AB. ∵CD ︵=CE ︵, ∴∠AOC =∠BOC. 在△AOC 和△BOC 中, ⎩⎪⎨⎪⎧∠AOC=∠BOC,OC =OC ,∠OCA =∠OCB=90°,∴△AOC ≌△BOC(ASA ).∴OA=OB ; (2)解:由(1)得AC =BC =12AB =2 3.在Rt △AOC 中,OC =OA 2-AC 2=2, ∴∠AOC =∠BOC=60°.S 扇形OCE =360=3π.∴S 阴影=S △BOC -S 扇形OCE =23-23π.正多边形与圆例3 (2018·宜宾中考)刘徽是中国古代卓越的数学家之一,他在《九章算术》中提出了“割圆术”,即用内接或外切正多边形逐步逼近圆来近似计算圆的面积.设⊙O 的半径为1,若用⊙O 的外切正六边形的面积S 来近似估计⊙O 的面积,则S =.(结果保留根号)【解析】依照题意画出图形如图.根据正多边形的定义可得出△ABO 为等边三角形,根据等边三角形的性质结合OM 的长度可求出AB 的长度,再利用三角形的面积公式即可求出S.,4.(2018·温州中考)小明发现相机快门打开过程中,光圈大小变化如图1所示,于是他绘制了如图2所示的图形.图2中六个形状大小都相同的四边形围成一个圆的内接正六边形和一个小正六边形,若PQ 所在的直线经过点M ,PB =5 cm ,小正六边形的面积为 4932cm 2,则该圆的半径为__8__cm .5.(2018·遵义中考)若要用一个底面直径为10,高为12的实心圆柱体,制作一个底面和高分别与圆柱底面半径和高相同的圆锥,则该圆锥的侧面积为( B )A .60πB .65πC .78πD .120π。
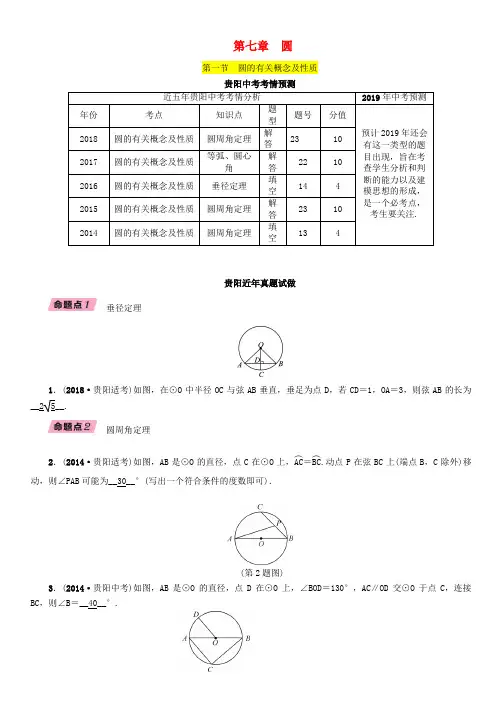
第七章 圆第一节 圆的有关概念及性质贵阳中考考情预测贵阳近年真题试做垂径定理1.(2018·贵阳适考)如图,在⊙O 中半径OC 与弦AB 垂直,垂足为点D ,若CD =1,OA =3,则弦AB 的长为 圆周角定理2.(2014·贵阳适考)如图,AB 是⊙O 的直径,点C 在⊙O 上,AC ︵=BC ︵.动点P 在弦BC 上(端点B ,C 除外)移动,则∠PAB 可能为__30__°(写出一个符合条件的度数即可).(第2题图)3.(2014·贵阳中考)如图,AB 是⊙O 的直径,点D 在⊙O 上,∠BOD =130°,AC ∥OD 交⊙O 于点C ,连接BC ,则∠B=__40__°.(第3题图)贵阳中考考点清单圆的有关概念续表圆的对称性圆周角中考典题精讲精练垂径定理例1 如图,C 是以AB 为直径的半圆O 上一点,连接AC ,BC ,分别以AC ,BC 为边向外作正方形ACDE ,BCFG.DE ,FG ,AC ︵,BC ︵的中点分别是M ,N ,P ,Q.若MP +NQ =14,AC +BC =18,则AB 的长为( C )A .9 2B .907C .13D .16【解析】连接OP ,OQ ,分别交AC ,BC 于点H ,I.根据DE ,FG ,AC ︵,BC ︵的中点分别是M ,N ,P ,Q ,得到OP⊥AC,OQ ⊥BC ,从而得到H ,I 是AC ,BC 的中点,利用中位线定理得到OH +OI =12(AC +BC)=9和PH +QI =18-14=4,从而利用AB =OP +OQ =OH +OI +PH +QI 求解.1.(2018·安顺中考)已知⊙O 的直径CD =10 cm ,AB 是⊙O 的弦,AB ⊥CD ,垂足为M ,且AB =8 cm ,则AC 的长为( C )A .2 5 cmB .4 5 cmC .2 5 cm 或4 5 cmD .2 3 cm 或4 3 cm2.(2018·遵义模拟)如图,AB ,BC 是⊙O 的两条弦,AB 垂直平分半径OD ,∠ABC =75°,BC =4 2 cm ,则O C 的长为__4__cm .圆周角定理例2 如图,在⊙O 中,AB ︵=AC ︵,∠AOB =40°,则∠ADC 的度数是( C )A .40°B .30°C .20°D .15°【解析】根据同圆或等圆中,同弧或等弧所对的圆周角相等,并且都等于所对圆心角的一半,可得∠ADC=12∠AOB=20°.3.(2018·遵义模拟)如图,⊙O是△ABC的外接圆,已知∠ABO=40°,则∠ACB的大小为( C)A.30°B.40°C.50°D.60°(第3题图)4.(2018·杭州中考)如图,AB是⊙O的直径,点C是半径OA的中点,过点C作DE⊥AB,交⊙O于D,E两点,过点D作直径DF,连接AF,则∠DFA=__30°__.(第4题图)。

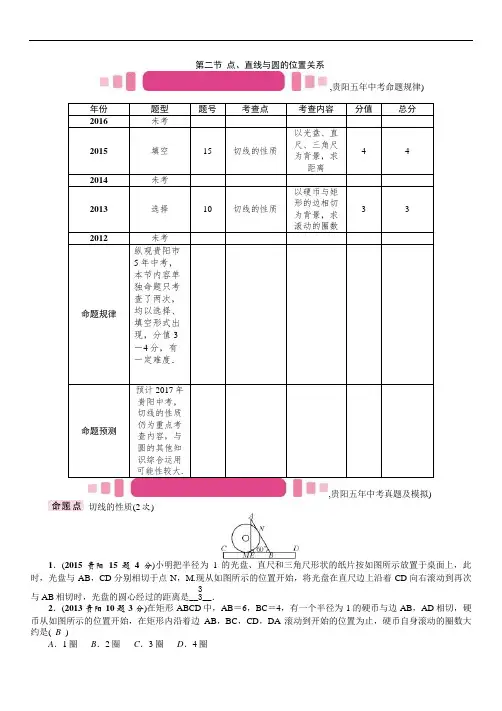
第二节 点、直线与圆的位置关系,贵阳五年中考命题规律)年份题型 题号考查点 考查内容分值总分 2016 未考2015 填空 15 切线的性质以光盘、直尺、三角尺为背景,求距离 4 4 2014 未考2013 选择 10 切线的性质以硬币与矩形的边相切为背景,求滚动的圈数3 3 2012未考命题规律 纵观贵阳市5年中考,本节内容单独命题只考查了两次,均以选择、填空形式出现,分值3-4分,有一定难度.命题预测 预计2017年贵阳中考,切线的性质仍为重点考查内容,与圆的其他知识综合运用可能性较大.,贵阳五年中考真题及模拟)切线的性质(2次)1.(2015贵阳15题4分)小明把半径为1的光盘、直尺和三角尺形状的纸片按如图所示放置于桌面上,此时,光盘与AB ,CD 分别相切于点N ,M.现从如图所示的位置开始,将光盘在直尺边上沿着CD 向右滚动到再次与AB 相切时,光盘的圆心经过的距离是__33__.2.(2013贵阳10题3分)在矩形ABCD 中,AB =6,BC =4,有一个半径为1的硬币与边AB ,AD 相切,硬币从如图所示的位置开始,在矩形内沿着边AB ,BC ,CD ,DA 滚动到开始的位置为止,硬币自身滚动的圈数大约是( B )A .1圈B .2圈C .3圈D .4圈(第2题图)(第3题图)3.(2015贵阳适应性考试)如图,AB 是⊙O 的直径,C ,D 是⊙O 上的点,∠CDB =30°,过点C 作⊙O 的切线交AB 的延长线于点E ,则sin E 的值为( A )A .21B .22C .23D .334.(2016原创)如图,在平面直角坐标系中,⊙O 的半径为1,则直线y =x -与⊙O 的位置关系是( B )A .相离B .相切C .相交D .以上三种情形都有可能5.(2015贵阳考试说明)如图,Rt △ABC 中,∠ACB =90°,AC =4,BC =6,以斜边AB 上的一点O 为圆心所作的半圆分别与AC ,BC 相切于点D ,E ,则AD 为( B )A .2.5B .1.6C .1.5D .1(第5题图)(第6题图)6.(2016贵阳模拟)如图,已知⊙O 的直径为AB ,AC ⊥AB 于点A ,BC 与⊙O 相交于点D ,在AC 上取一点E ,使得ED =EA.(1)求证:ED 是⊙O 的切线;(2)当OA =3,AE =4时,求BC 的长度.解:(1)如图,连接OD.∵OD =OA ,EA =ED ,∴∠3=∠4,∠1=∠2.∴∠1+∠3=∠2+∠4,即∠ODE =∠OAE.∵AB ⊥AC ,∠OAE =90°,∴∠ODE =90°,∴DE 是⊙O 的切线;(2)∵OA =3,AE =4,∴OE =5.又∵AB 是直径,∴AD ⊥BC ,∴∠1+∠5=90°,∠2+∠6=90°.又∵∠1=∠2,∴∠5=∠6,∴DE =EC ,∴E 是AC的中点,又∵O 为AB 中点,∴OE 为△ABC 的中位线,∴OE ∥BC 且OE =21BC ,∴BC =10.,中考考点清单)点与圆的位置关系(设r 为圆的半径,d 为点到圆心的距离)1.位置关系,点在圆内,点在圆上,点在圆外 数量(d 与r)的大小关系,__d <r __,__d =r __,__d >r __ 直线与圆的位置关系(设r 为圆的半径,d 为圆心到直线的距离)2.位置关系,相离,相切,相交 公共点个数,0,1,2公共点的名称,无,切点,交点数量关系,__d >r __,__d =r __,__d <r __ 切线的性质与判定(高频考点)3.判定切线的方法有三种:①利用切线的定义,即与圆有__唯一公共点__的直线是圆的切线;②到圆心的距离等于__半径__的直线是圆的切线;③经过半径的外端点并且__垂直__于这条半径的直线是圆的切线.4.切线的五个性质:①切线与圆只有__一个__公共点;②切线到圆心的距离等于圆的__半径__;③切线垂直于经过切点的__半径__;④经过圆心垂直于切线的直线必过__切点__;⑤经过切点垂直于切线的直线必过__圆心__.切线长定理5.经过圆外一点作圆的切线,这点与__切点__之间的线段的长度,叫做这点到圆的切线长.经过圆外一点可以引圆的两条切线,它们的切线长__相等__,这一点和圆心的连线平分两条切线的__夹角__.三角形的外心和内心6.三角形的外心:三角形外接圆的圆心,是三角形__三边垂直平分线__的交点,到__三角形三个顶点的距离__相等.7.三角形的内心:三角形内切圆的圆心,是三角形__三条角平分线__的交点,到__三角形三边的距离__相等.【方法点拨】1.判断直线与圆相切时:(1)直线与圆的公共点已知时,连半径证垂直;(2)直线与圆的公共点未知时,过圆心作直线的垂线证垂线段等于半径.2.利用切线的性质解决问题,通常连过切点的半径,构造直角三角形来解决.3.直角三角形的外接圆与内切圆半径的求法:若a 、b 是Rt △ABC 的两条直角边,c 为斜边,则(1)直角三角形的外接圆半径R =2c ;(2)直角三角形的内切圆半径r =2a +b -c.,中考重难点突破)点与圆和直线与圆的位置关系【例1】(2016宜昌中考)在公园的O 处附近有E ,F ,G ,H 四棵树,位置如图所示(图中小正方形的边长均相等),现计划修建一座以O 为圆心,OA 为半径的圆形水池,要求池中不留树木,则E ,F ,G ,H 四棵树中需要被移除的为( )A .E ,F ,GB .F ,G ,HC .G ,H ,ED .H ,E ,F【解析】设小正方形的边长为1,由点在图中的位置和勾股定理可知,OG =1,OE =OF =2,OA ==,OH ==2,∴OG<OE =OF<OA<OH ,∴需要被移除的树是E ,F ,G.【学生解答】A1.(2016台州中考)如图,在△ABC 中,AB =10,AC =8,BC =6,以边AB 的中点O 为圆心,作半圆与AC相切,点P ,Q 分别是边BC 和半圆上的动点,连接PQ ,则PQ 长的最大值与最小值的和是( C )A .6B .2+1C .9D .3222.(2014白银中考)已知⊙O 的半径是6 cm ,点O 到同一平面内直线l 的距离为5 cm ,则直线l 与⊙O 的位置关系是( A )A .相交B .相切C .相离D .无法判断切线的性质及判定【例2】(2016海南中考)如图,AB 是⊙O 的直径,直线PA 与⊙O 相切于点A ,PO 交⊙O 于点C ,连接BC ,若∠P =40°,则∠ABC 的度数为( )A .20°B .25°C .40°D .50°【解析】根据切线的性质可知:∠PAO =90°.又∵∠P =40°.在Rt △PAO 中,∠POA =90°-40°=50°,又根据圆周角定理可得:∠ABC =21∠AOP =21×50°=25°.【学生解答】B3.(2016潍坊中考)如图,在平面直角坐标系中,⊙M 与x 轴相切于点A(8,0),与y 轴分别交于点B(0,4)与点C(0,16),则圆心M 到坐标原点O 的距离是( D )A .10B .8C .4D .2,(第3题图)) ,(第4题图))4.(2016包头中考)如图,已知AB 是⊙O 的直径,点C 在⊙O 上,过点C 的切线与AB 的延长线交于点P ,连接AC.若∠A =30°,PC =3,则BP 的长为____.5.(2016宁波中考)如图,已知⊙O 的直径AB =10,弦AC =6,∠BAC 的平分线交⊙O 于点D ,过点D 作DE ⊥AC 交AC 的延长线于点E.(1)求证:DE 是⊙O 的切线; (2)求DE 的长.证明:(1)连接OD ,∵AD 平分∠BAC ,∴∠DAE =∠DAB ,∵OA =OD ,∴∠ODA =∠DAO ,∴∠ODA =∠DAE ,∴OD ∥AE ,∵DE ⊥AC ,∴OD ⊥DE ,∴DE 是⊙O 的切线;(2)过点O 作OF ⊥AC 于点F ,∴AF =CF =3,∴OF ===4.∵∠OFE =∠DEF =∠ODE =90°,∴四边形OFED 是矩形,∴DE =OF =4.6.(2016自贡中考)如图,⊙O 是△ABC 的外接圆,AC 为直径,弦BD =BA ,BE ⊥DC 交DC 的延长线于点E.求证:(1)∠1=∠BAD;(2)BE是⊙O的切线.证明:(1)∵BD=BA,∴∠BDA=∠BAD,∵∠1=∠BDA,∴∠1=∠BAD;(2)连接BO,∵∠ABC=90°,又∵∠BAD+∠BCD=180°,∴∠1+∠BCD=180°,∵OB=OC,∴∠1=∠CBO,∴∠CBO+∠BCD=180°,∴OB∥DE,∵BE⊥DE,∴EB⊥OB,∵OB是⊙O的半径,∴BE是⊙O的切线.。

第三节 正多边形与圆的有关计算(时间:45分钟)1.(2018·宁波中考)如图,在△ABC 中,∠ACB =90°,∠A =30°,AB =4,以点B 为圆心,BC 长为半径画弧,交边AB 于点D ,则CD ︵的长为( C )A .16πB .13πC .23πD .233π2.(2018·黄石中考)如图,AB 是⊙O 的直径,点D 为⊙O 上一点,且∠ABD=30°,BO =4,则BD ︵的长为( D )A .23πB .43πC .2πD .83π3.如图,△ABC 内接于⊙O,∠A =60°,BC =63,则BC ︵的长为( B )A .2πB .4πC .8πD .12π4.(2018·遵义模拟)如图,在△AB C 中,∠C =90°,AC >BC ,若以AC 为底面圆半径,BC 为高的圆锥的侧面积为S 1,以BC 为底面圆半径,AC 为高的圆锥的侧面积为S 2,则( B )A .S 1=S 2B .S 1>S 2C .S 1<S 2D .S 1,S 2的大小关系不确定5.(2018·温州中考)已知扇形的弧长为2π,圆心角为60°,则它的半径为__6__.6.(2018·湖州中考)如图,已知AB 是⊙O 的直径,C ,D 是⊙O 上的点,OC ∥BD ,交AD 于点E ,连接B C . (1)求证:AE =ED ;(2)若AB =10,∠CBD =36°,求AC ︵的长.(1)证明:∵AB 是⊙O 的直径, ∴∠ADB =90°. ∵OC ∥BD ,∴∠AEO =∠ADB=90°, 即OC⊥AD. ∴AE =ED ;(2)解:∵OC⊥AD,∴AC ︵=CD ︵. ∴∠ABC =∠CBD=36°.∴∠AOC =2∠ABC=2×36°=72°. ∴AC ︵的长为72π×5180=2π.7.(2018·湖州中考)尺规作图特有的魅力曾使无数人沉湎其中.传说拿破仑通过下列尺规作图考他的大臣: ①将半径为r 的⊙O 六等分,依次得到A ,B ,C ,D ,E ,F 六个分点; ②分别以点A ,D 为圆心,AC 长为半径画弧,G 是两弧的一个交点; ③连接OG.问:OG 的长是多少?大臣给出的正确答案应是( D )A .3rB .⎝ ⎛⎭⎪⎫1+22r C .⎝ ⎛⎭⎪⎫1+32r D .2r8.如图,四边形OABC 为菱形,点B ,C 在以点O 为圆心的EF ︵上,若OA =1,∠1=∠2,则扇形OEF 的面积为( C )A .π6B .π4C .π3D .2π39.如图,两个正六边形的边长均为1,其中一个正六边形的一边恰在另一个正六边形的对角线上,则这个图形(阴影部分)外轮廓线的周长是( B )A .7B .8C .9D .1010.如图,在△ABC 中,AB =AC ,AB =8,BC =12,分别以AB ,AC 为直径作半圆,则图中阴影部分的面积是( D )A .64π-127B .16π-32C .16π-247D .16π-12711.(2018·毕节模拟)如图,把正六边形各边按同一方向延长,使延长的线段与原正六边形的边长相等,顺次连接这六条线段外端点可以得到一个新的正六边形,重复上述过程,经过10次后,所得到的正六边形是原正六边形边长的__243__倍.12.(2018·株洲中考)如图,正五边形ABCDE 和正三角形AMN 都是⊙O 的内接多边形,则∠BOM=__48°__.13.(2018·临沂中考)如图,在△ABC 中,∠A =60°,BC =5 cm .能够将△ABC 完全覆盖的最小圆形纸片的直径是3cm .14.(2018·德州中考)如图,AB 是⊙O 的直径,直线CD 与⊙O 相切于点C ,且与AB 的延长线交于点E.点C 是BF ︵的中点.(1)求证:AD⊥CD;(2)若∠CAD=30°,⊙O 的半径为3,一只蚂蚁从点B 出发,沿着BE -EC -CB ︵爬回至点B ,求蚂蚁爬过的路程(π≈3.14,3≈1.73,结果保留一位小数).(1)证明:连接OC.∵直线CD 是⊙O 的切线,∴OC⊥CD. ∴∠OCE =90°. ∵点C 是BF ︵的中点, ∴∠CAD =∠CAB.∵OA =OC ,∴∠CAB =∠ACO. ∴∠CAD =∠ACO.∴AD∥CO. ∴∠ADC =∠OCE=90°.∴AD ⊥CD ; (2)解:∵∠CAD=30°, ∴∠CAB =∠CAD=30°. ∴∠COE =2∠CAB=60°.∵直线CD 是⊙O 的切线,∴OC ⊥CD.∴∠OCE =90°,∴∠E =180°-90°-60°=30°. ∵OC =3,∴OE =2OC =6.∴CE=3OC =3 3. ∴BE =OE -OB =3. ∴BC ︵的长l =60π×3180=π.∴蚂蚁爬过的路程为3+33+π≈11.3.。
