第五节：微分

2. 函数和,差,积,商的微分法则 函数和,
d(u ± v) = du ± dv d(uv) = vdu + udv
d(Cu) = Cdu u vdu udv d( ) = v v2
例2 设 y = ln( x + e ), 求dy.
x2
解 例3
Q y′ =
1 + 2xe x + ex
x2
2
,
∴dy =
x0 + x
x
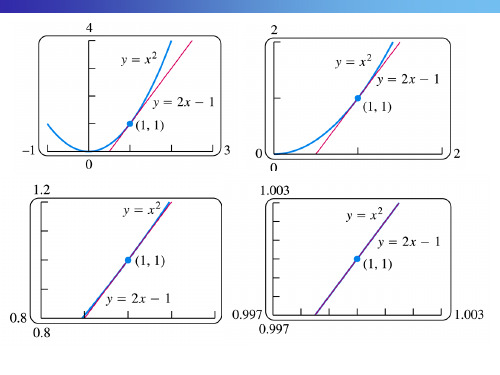
, M , 当x 很小时 在点 的附近
切线段 MP 可近似代替曲线段 MN.
五,微分的求法
dy = f ′( x)dx
求法: 计算函数的导数, 乘以自变量的微分. 求法: 计算函数的导数 乘以自变量的微分 1.基本初等函数的微分公式 基本初等函数的微分公式
d(C) = 0 d(sin x) = cos xdx d( x ) = x1dx d(cos x) = sin xdx
例5 在下列等式左端的括号中填入适当的函数 使 在下列等式左端的括号中填入适当的函数,使 等式成立. 等式成立
(1) d( ) = cos ωtdt;
(2) d(sin x ) = ( )d( x).
2
解 (1)Qd(sin ωt ) = ωcos ωtdt ,
1 1 ∴cos ωtdt = d(sin ωt ) = d( sin ωt ); ω ω 1 ∴d( sin ωt + C) = cos ωtdt. ω d(sin x2 ) 2x cos x2dx (2)Q = = 4x x cos x2 , 1 d( x) dx 2 x ∴d(sin x2 ) = (4x x cos x2 )d( x).
y = f ( x)在点x0可微, 并且称 A x 为函数 y = f ( x)在点x0相应于自变量增量 x的微分 ,
记作dy x=x0 或df ( x0 ), 即dy x=x0 = A x.
. 微分的实质) 微分dy叫做函数增量y的线性主部(微分的实质)
y = f ( x0 + x) f ( x0 ) = A x + o(x) = dy x=x0 + o(x).
几个常用的近似公式( 很小时) 几个常用的近似公式(x 很小时) 1 n (1) 1 + x ≈ 1 + x ; n (2) sin x ≈ x ( x的单位 弧度); :
(3) tan x ≈x ( x的单位 弧度); :
(4) e x ≈ 1 + x ;
(5) ln(1 + x) ≈x .
厘米的球, 例1:一个外直径为 10 厘米的球,球壳厚 : 1 厘米,求球壳体积的近似值. 度为 厘米,求球壳体积的近似值.
2 A = ( x0 + x)2 x0 = 2x0 x + (x)2 .
(1) )
1 1 2 1 2 ) s = g(t0 + t ) gt0 = gt0 t + g(t )2 (2) 2 2 2
所以我们可以将(1)和(2)写成统一形式 所以我们可以将( ) )
A = α( x0 ) x + o(x), s = β (t0 ) t + o(t ).
∴y = A x + o(x),
y o(x) , ∴ = A+ x x
o(x) y 则 lim = A+ lim = A. x→0 x x→0 x
, 即函数 f ( x)在点x0可导 且A = f ′( x0 ).
三,可微的条件
定理 函数 f ( x)在点x0可微的充要条件是函 数 f ( x)在 x0处 导 且 A = f ′( x0 ). 点 可 , 证 (2) 充分性 Q函数f ( x)在点 x0 可导 ,
即dy |x=x0 = f ′( x0 )x.
(2) 函数 y = f ( x)在区间I 上任意点x的微分, 可表为
dy = f ′( x) x
. 例1 求函数 y = x 当x = 2, x = 0.02时的微分
3
解 Qdy = ( x3 )′x = 3x2x.
∴dy x=2
x=0.02
= 3x2x x=2
x 设边长由 0变到x0 + x,
x0
x
(x)2
x
Q正方形面积 A= x , =
∴A = ( x0 + x)2 x
(1) (2)
2 0 2 0
x0x
A= x0 = 2
= 2x0 x + (x)2 .
(1) : x的线性函数且为 A的主要部分 , ; (2) : x的高阶无穷小当x 很小时可忽略 , .
第五节 函数的微分
一,问题的提出 二,微分的定义 三,可微的条件 四,微分的几何意义 五,微分的求法 六,微分形式的不变性 七,微分在近似计算中的应用
一,问题的提出
实例1:正方形金属薄片受热后面积的改变量. 实例1:正方形金属薄片受热后面积的改变量 1:正方形金属薄片受热后面积的改变量
七,微分在近似计算中的应用
1. 函数的近似计算
当x很小 且 f ′( x0 ) ≠ 0时 , ,
y ≈ dy = f ′( x0 ) x
(1)
Qy = f ( x0 + x) f ( x0 ) 令 x = x0 + x, 则 f ( x) ≈ f ( x0 ) + f ′( x0 )( x x0 )
六,微分形式的不变性
设函数 y = f ( x)有导数 f ′( x),
(1) 若x是自变量时 dy = f ′( x)dx; ,
(2) 若x是中间变量时 即另一变量 t 的可 , 微函数x = (t ), 则 d x = ′(t )dt, y = f [(t)]
d f [(t )] dy = dt = f ′( x)′(t ) dt = f ′( x)dx. dt
(5) 当x 很小时 y ≈ dy (线性主部 , ).
上处处可微, 如果函数 y = f (x) 在区间 I 上处处可微,则称 f (x) 上可微. 在区间 I 上可微.
, 函数 y = f ( x)在区间I 上任意点x的微分 称为函 , 数的微分 记作 dy或df ( x), 即dy = A( x)x.
y ∴ lim = f ′( x0 ), x→0 x
y 即 = f ′( x0 ) + α, x
从而 y = f ′( x0 ) x + α (x), = f ′( x0 ) x + o(x),
Qα → 0 (x → 0),
Q函数 f ( x)在点x0可微, 且 f ′( x0 ) = A.
(1) 可导可微, 且A = f ′( x0 ),
两个基本问题: 两个基本问题: (1)函数可微的条件是什么? )函数可微的条件是什么? (2)若函数可微,则定义中的 A (x) = ? )若函数可微,
三,可微的条件
定理 函数 f ( x)在点x0可微的充要条件是函 数 f ( x)在 x0处 导 且 A = f ′( x0 ). 点 可 , 证 (1) 必要性 Q f ( x)在点 x0 可微,
= 0.24.
x=0.02
的微分: 例2:考虑函数 y = x 的微分: :
d y = d x = ( x)' x = x
即d x = x.
. 通常把自变量x的增量x称为自变量的微分 dy = f ′(x). ∴dy = f ′( x)x = f ′( x)d x dx
即函数的微分dy 与自变量的微分d x 之商等于 " ". 该函数的导数. 导数也叫 微商
结论: 结论:无论x是自变量还是中间变量, 函数 y = f (x)的微分形式总是 dy = f ′( x)dx 微分形式的不变性
例3 设 y = sin(2x + 1), 求dy. 解 Q y = sin u, u = 2x + 1.
∴dy = cos udu = cos(2x + 1)d(2x + 1) = cos(2x + 1) 2dx = 2cos(2x + 1)dx.
1 + 2xe x + ex
x2
2
dx.
设 y = e13 x cos x, 求dy.
解 dy = cos x d(e13x ) + e13x d(cos x)
Q(e
13 x
′ = 3e13 x , (cos x)′ = sin x. )
13 x
∴dy = cos x (3e13 x )dx + e13 x ( sin x)dx = e (3cos x + sin x)dx.
d(tan x) = sec2 xdx d(cot x) = csc2 xdx d(sec x) = sec x tan xdx d(csc x) = csc x cot xdx
d(ax ) = ax lnadx d(ex ) = exdx 1 1 d(loga x) = dx d(ln x) = dx x lna x 1 1 d(arcsin x) = dx d(arccos x) = dx 2 2 1 x 1 x 1 1 d(arctan x) = d(arc cot x) = 2 dx 2 dx 1+ x 1+ x
由定义知: 由定义知:
(1) dy是自变量的改变量 x的线性函数 ;
(2) y dy = o(x)是比x高阶无穷小 ;
(3) 当A ≠ 0时, dy与y是等价无穷小 ;
y o(x) Q = 1+ →1 (x → 0). dy A x
(4) A是与 x无关的常数 但与 ( x)和x0有关 , f ;