大学物理(西南交大)作业参考答案1

©物理系_2015_09《大学物理CII》作业No.7 热力学第二定律班级________ 学号________ 姓名_________ 成绩_______一、判断题：（用“T”和“F”表示）[ F ] 1．在任意的绝热过程中，只要系统与外界之间没有热量传递，系统的温度就不会发生变化。

此说法不对．在绝热过程中，系统与外界无热量交换，Q=0．但不一定系统与外界无作功，只要系统与外界之间有作功的表现，由热力学第一定律Q=E+W，可知，E=-W，即对应有内能的改变．而由E=νC，T可知，有E，一定有T，即有温度的变化．[ F ] 2．在循坏过程中系统对外做的净功在数值上等于p-V图中封闭曲线所包围的面积，因此封闭曲线包围的面积越大，循坏效率就越高。

有人说，因为在循环过程中系统对外做的净功在数值等于p-V图中封闭曲线所包围的面积，所以封闭曲线所包围的面积越大，循环效率就越高，对吗？答：不正确，因为循环效率取决于系统对外做的净功和系统由高温热源吸收的热量，只有在从高温热源吸收的热量一定的情况下，封闭曲线所包围的面积越大，即系统对外所做的净功越多，循环效率越高，如果从高温热源吸收的热量不确定，则循环效率不一定越高[ F ] 3．系统经历一正循坏后，系统与外界都没有变化。

系统经历一正循环后，系统的状态没有变化；（２）系统经历一正循环后，系统与外界都没有变化；（３）系统经历一正循环后，接着再经历一逆循环，系统与外界亦均无变化。

解说法（1）正确，系统经历一正循环后，描述系统状态的内能是单值函数，其内能不变，系统的状态没有变化。

说法（2）错误，系统经过一正循环，系统内能不变，它从外界吸收热量，对外作功，由热力学第二定律知，必定要引起外界的变化。

说法（3）错误，在正逆过程中所引起外界的变化是不能消除的。

[ F ] 4.第二类永动机不可能制成是因为违背了能量守恒定律。

解：第二类永动机并不违背能量守恒定律，但它违背了热力学第二定律。

No.3 角动量、角动量守恒定律一、选择题： 1．D解：设地球绕太阳做圆周运动的速率为v ，轨道角动量为L ，由万有引力定律和牛顿运动定律 R v m R m M G 22=可得 GMR m mvR L RGMv ===,2．B解：设棒长为l ，质量为m ，在向下摆到角θ时，由转动定律βθJ lmg =⋅cos 2（J 为转动惯量） 在棒下摆过程中，θ增大，β减小。

棒由静止开始下摆，ω与β转向一致，所以由小变大。

3．C解：设A 、B 连盘厚度为d ，半径分别为A R 和B R ，由题意，二者质量相等，即 B B A A d R d R ρπρπ22=因为B A ρρ>，所以22B A R R <，由转动惯量221mR J =，则B A J J <。

4．B解： （1）对转轴上任一点，力矩为F r M ⨯=。

若F 与轴平行，则M一定与轴垂直，即对轴的力矩0=z M ，两个力的合力矩一定为零。

正确。

（2）两个力都垂直于轴时，对轴上任一点的力矩都平行于轴，若二力矩大小相等，方向相反，则合力矩为零。

正确。

（3）两个力的合力为零，如果是一对力偶，则对轴的合力矩不一定为零。

（4）两个力对轴的力矩只要大小相等，符号相反，合力矩就为零，但两个力不一定大小相等，方向相反，即合力不一定为零。

5．C解：以两个子弹和圆盘为研究对象，外力矩为零，系统角动量守恒。

设圆盘转动惯量为J ，则有 ()ωω202mr J J mvr mvr +=+-022ωωmr J J+=可见圆盘的角速度减小了。

m二、填空题：1． M = 0 ； L= k ab m ω 。

解：由j t b i t a rωωsin cos +=，质点的速度和加速度分别为jt b i t a a jt b i t a vωωωωωωωωsin cos cos sin 22--=+-= 质点所受对原点的力矩为M a m r F r⨯=⨯=()()0sin cos sin cos 22=--⨯+=jt mb i t ma j t b i t a ωωωωωω质点对原点的角动量为()()j t mb i t ma j t b i t a v m r Lωωωωωωcos sin sin cos +-⨯+=⨯= k ab mω=2． M =mgl β=lg 。

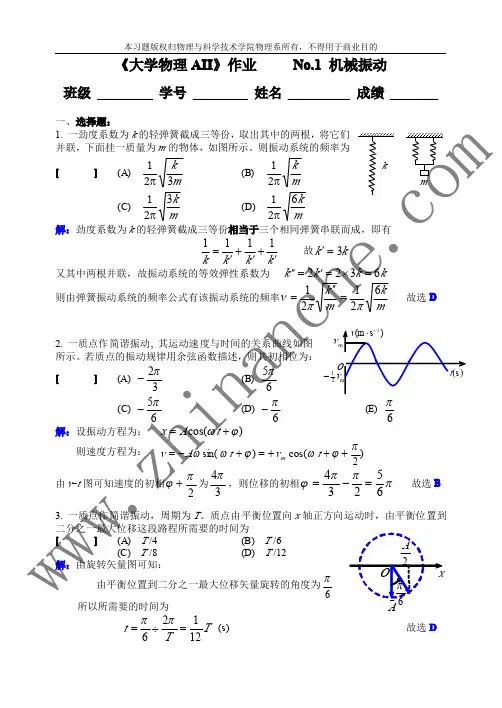
西南交大峨眉校区《大学物理》（机械振动）作业1一 选择题1. 把一弹簧振子的小球从平衡位置向位移正方向拉开，然后由静止放手任其振动，从放手时开始计时．若用余弦函数表示其运动方程，则该弹簧振子振动的初相为 (A) 0． (B) π/2． (C) π． (D) 3π/2．［ A ］[参考解答] 开始计时时，位移达到最大值。

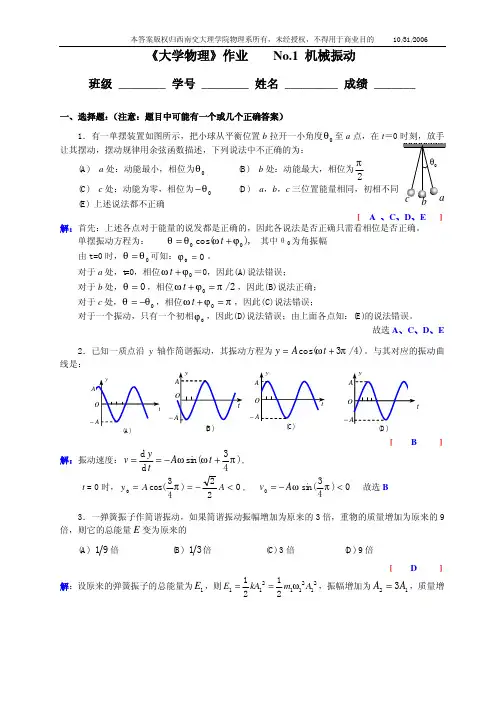
2. 一质点在x 轴上作简谐振动，振幅A=4cm,周期T=2s ，其平衡位置取作坐标原点，若t=0s 时刻质点正通过x=-2cm 处，且向x 轴负方向运动，则质点下一次通过x=-2cm 处的时刻为： （A ）1s （B ）2s/3 （C ）4s/3 （D ）2s［ B ］3．一弹簧振子作简谐振动，当其偏离平衡位置的位移的大小为振幅的1/4时，其动能为振动总能量的（A ）7/16 （B ）9/16（C ）11/16 （D ）13/16 （E ）15/16[ E ][参考解答] 4/)cos(A t A x =+=ϕω，16/15)(sin ,4/1)cos(2=+=+ϕωϕωt t 即，1615)(sin max2max k k k E t E E =+=ϕω4．图中所画的是两个简谐振动的振动曲线，若这两个简谐振动可叠加，则合成的余弦振动的初相位为： （A ）2π（B ）π （C ）23π （D ）0[ B ][参考解答] t=0时刻的旋转矢量图：OA/2-AA 合cm ）1.一竖直悬挂的弹簧振子，自然平衡时弹簧的伸长量为x 0，此振子自由振动的周期T = g x /20π．[参考解答] 受力分析如右图，以平衡位置为原点，向下为x 轴正方向，有：22/22)/(dtX d mkX k mg x k mg kx dtx d m kmg x X =-=--=+-=-=令对坐标X ，其运动为简谐运动， 其角频率满足：，mk =2ωg x T /2/20πωπ==2. 一质点作简谐振动，速度最大值v m = 5 cm/s ，振幅A = 2 cm ．若令速度具有正最大值的那一时刻为t = 0，则振动表达式为 )()2325cos(2cm t x π+=．[参考解答] s rad cm A A v m /5.2,2,=∴==ωωt =0时，质点通过平衡位置向正方向运动，初相为：230πϕ=3．一弹簧简谐振子的振动曲线如图所示，振子处在位移为零，速度为－ωA ，加速度为零和弹性力为零的状态，对应于曲线上的 b, f 点，振子处在位移的绝对值为A 、速度为零、加速度为－ω2A 和弹性力为－KA 的状态，则对应于曲线上的 a, e 点。

NO.1 质点运动学班级 姓名 学号 成绩一、选择1. 对于沿曲线运动的物体，以下几种说法中哪种是正确的： [ B ](A) 切向加速度必不为零．（反例：匀速圆周运动） (B) 法向加速度必不为零（拐点处除外）．(C) 由于速度沿切线方向，法向分速度必为零，因此法向加速度必为零．（反例：匀速圆周运动）(D) 若物体作匀速率运动，其总加速度必为零．（反例：匀速圆周运动） (E) 若物体的加速度a为恒矢量，它一定作匀变速率运动．2．一质点作一般曲线运动，其瞬时速度为V，瞬时速率为V ，某一段时间内的平均速度为V，平均速率为，它们之间的关系为：[ D ]（A ）∣V∣=V ，∣V∣=V；（B ）∣V∣≠V ，∣V∣=V ；（C ）∣V∣≠V ，∣V∣≠V ； （D ）∣V∣=V ，∣V∣≠V .解：dr dsV V dt dt=⇒=，r sV V t t∆∆≠⇒≠∆∆.3.质点作曲线运动，r表示位置矢量，v表示速度，a表示加速度，S 表示路程，a τ表示切向加速度，下列表达式中， [ D ](1) d /d t a τ=v ， (2) v =t r d /d ， (3) v =t S d /d ， (4) d /d t a τ=v ． (A) 只有(1)、(4)是对的． (B) 只有(2)、(4)是对的．(C) 只有(2)是对的． (D) 只有（1）、(3)是对的．解：d /d t a τ=v ，v=t S d /d ， at v=d /d4.质点作半径为R 的变速圆周运动时的加速度大小为 (v 表示任一时刻质点的速率) [ D ](A) t d d v ．(B) 2v R ． (C) R t 2d d vv +．(D) 2/1242d d ⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛R t v v ．解：a==5.一质点在平面上运动，已知质点位置矢量的表示式为jbtiatr22+=（其中a、b为常量）, 则该质点作[ B](A) 匀速直线运动．(B) 变速直线运动．(C) 抛物线运动．(D)一般曲线运动．解：可以算出by xa=，同时2xa a=、2ya b=，所以严格地讲：匀变速直线运动。

电势、导体与※电介质中的静电场 （参考答案）班级： 学号： 姓名： 成绩： 一 选择题1．真空中一半径为R 的球面均匀带电Q ，在球心O 处有一带电量为q 的点电荷，如图所示，设无穷远处为电势零点，则在球内离球心O 距离为r 的P 点处的电势为：（A ）r q04πε； （B ）)(041R Qrq +πε； （C ）rQq 04πε+； （D ）)(041R qQ rq -+πε；参考：电势叠加原理。

[ B ]2．在带电量为-Q 的点电荷A 的静电场中，将另一带电量为q 的点电荷B 从a 点移动到b ，a 、b 两点距离点电荷A 的距离分别为r 1和r 2，如图，则移动过程中电场力做功为：（A ）)(210114r r Q --πε； （B ）)(21114r r qQ-πε；（C ）)(210114r r qQ--πε； （D ）)(4120r r qQ --πε。

参考：电场力做功＝势能的减小量。

A=W a -W b ＝q(U a -U b ) 。

[ C ]3N 点，有人（A ）电场强度E M ＜E N ； （B ）电势U M ＜U N ； （C ）电势能W M ＜W N ； （D ）电场力的功A ＞0。

r 2 (-Qbr 1B a（q ）[ C ]4．一个未带电的空腔导体球壳内半径为R ，在腔内离球心距离为d （d ＜R ）处，固定一电量为+q 的点电荷，用导线把球壳接地后，再把地线撤去，选无穷远处为电势零点，则球心O 处的点势为： （A ）0； （B ）d q04πε； （C ）-R q04πε； （D ）)(1140R dq-πε。

外表面无电荷（可分析）。

虽然内表面电荷分布不均，但到O 点的距离相同，故由电势叠加原理可得。

[ D ]※5．在半径为R 的球的介质球心处有电荷+Q ，在球面上均匀分布电荷-Q ，则在球内外处的电势分别为： （A ）内r Qπε4+，外r Q 04πε-； （B ）内r Qπε4+，0； 参考：电势叠加原理。

大学物理答案第八章西南交大版第八章相对论8-1 选择题v(1)一火箭的固有长度为L，相对于地面作匀速直线运动的速度为，火箭上有一个1v人从火箭的后端向火箭前端上的一个靶子发射一颗相对于火箭的速度为的子弹。

在火箭2上测得子弹从射出到击中靶的时间间隔是:LL(A) (B) v，vv122LL(C) (D) [B] 2v,v21，，v1,v/c11v解:在火箭参考系中，子弹以速率，匀速通过距离L，所需的时间 2L ,t,v2(2)关于同时性有人提出以下一些结论，其中哪个是正确的,(A)在一惯性系同时发生的两个事件，在另一惯性系一定不同时发生。

(B)在一惯性系不同地点同时发生的两个事件，在另一惯性系一定同时发生。

(C)在一惯性系同一地点同时发生的两个事件，在另一惯性系一定同时发生。

(D)在一惯性系不同地点不同时发生的两个事件，在另一惯性系一定不同时发生。

[C]u,,,解:由洛仑兹变换,可知: ,t,,t,,x,,2c,,,,t,0,,x,0,t,0当时，即在一个惯性系中同时同地发生的两个事件，在另一惯性系中一定同时发生;,,t,0,,x,0,t,0当时即在一个惯性系中的同时异地事件，在另一惯性系中必然不同时。

,,x,0,,t,0,t当时的大小有各种可能性，不是必然不为零的。

(3)一宇宙飞船相对地球以0.8c(c表示真空中光速)的速度飞行，一光脉冲从船尾传到船头，飞船上的观察者测得飞船长为90m，地球上的观察者测得脉冲从船尾发出和到达船头两个事件的空间间隔为65(A)90m (B)54m (C)270m (D)150m [C],,ss系，飞船系为系。

系相对于系沿x轴方向以飞行，解:设地球系为u,0.8css1,, 21,0.890,,,s,x,90m系中， ,t,c,,，，x,,x，ut由洛仑兹坐标变换得,,，，,x,,,x，u,t190,,,90，0.8c，,,2 c,,1,0.8,270m163.6，10J(4)某核电站年发电量为100亿度，它等于的能量，如果这是由核材料的全部静止能转化产生的，则需要消耗的核材料的质量为 (A)0.4kg (B)0.8kg 77(C) (D) [A] ，，12，10kg1/12，10kg2解:由质能关系 E,mc0016E3.6，100 m,,,0.4kg0228c，，3，10(5)设某微观粒子的总能量是它的静止能量的K倍，则其运动速度的大小cc2(A) (B) 1,KK,1Kcc2(C) (D) [C] ，，K,1KK，2K，1K22解:由质能关系 E,mc,E,mc00Em ,,KEm00m0m,又由质速关系 2u,,1,,,c,,661,K 得 2u,,1,,,c,,c2 u,k,1K8-2 填空题,6(1)子是一种基本粒子，在相对于子静止的坐标系中测得其寿命为。

《大学物理学》课后习题参考答案习题11-1. 已知质点位矢随时间变化函数形式为)ωｔsin ωｔ(cos j i R r其中为常量．求：（1）质点轨道；(2)速度和速率。

解：1）由)ωｔsin ωｔ(cos j i R r知t cos R x ωtsin R yω消去t 可得轨道方程222Ryx2）jr vt Rcos sin ωωt ωR ωdtd iRωt ωR ωt ωR ωv2122])cos ()sin [(1-2. 已知质点位矢随时间变化的函数形式为j ir )t 23(t 42，式中r 的单位为m ，t 的单位为s .求：（1）质点的轨道；（2）从0t到1t 秒的位移；（3）0t 和1t 秒两时刻的速度。

解：1）由j ir)t 23(t 42可知2t 4x t23y消去t 得轨道方程为：2)3y(x2）jir v 2t 8dtd jij i v r 24)dt2t 8(dt101Δ3）jv 2(0)jiv 28(1)1-3. 已知质点位矢随时间变化的函数形式为j ir t t 22，式中r 的单位为m ，t 的单位为s .求：（1）任一时刻的速度和加速度；（2）任一时刻的切向加速度和法向加速度。

解：1）ji r v2t 2dtd iv a2dtd 2）212212)1t(2]4)t 2[(v1tt 2dtdv a 2t22221nta aat 1-4. 一升降机以加速度a 上升，在上升过程中有一螺钉从天花板上松落，升降机的天花板与底板相距为d ，求螺钉从天花板落到底板上所需的时间。

解：以地面为参照系，坐标如图，升降机与螺丝的运动方程分别为20121att v y （1）图 1-420221gttv h y （2）21y y （3）解之2d tg a 1-5. 一质量为m 的小球在高度h 处以初速度0v 水平抛出，求：（1）小球的运动方程；（2）小球在落地之前的轨迹方程；（3）落地前瞬时小球的td dr ，td dv ，tv d d .解：（1）t v x 0式（1）2gt21hy 式（2）jir )gt 21-h (t v (t)20（2）联立式（1）、式（2）得22v 2gx hy （3）ji r gt -v td d 0而落地所用时间gh 2t所以j i r 2gh -v t d d 0jv g td d 2202y2x)gt (vvvv 211222222[()](2)g ghg t dv dtvgt vgh 1-6. 路灯距地面的高度为1h ，一身高为2h 的人在路灯下以匀速1v 沿直线行走。

©西南交大物理系_2013_02《大学物理AI 》作业No.03角动量角动量守恒定律班级________学号________姓名_________成绩_______一、判断题：（用“T ”和“F ”表示）[F ]1．如果一个刚体所受合外力为零，其合力矩一定为零。

解：合力为零，合力矩不一定为零。

反之亦然。

[F]2．一个系统的动量守恒，角动量一定守恒。

解：动量守恒的条件是合外力为零，角动量守恒的条件是合外力矩为零。

理由同上题一样。

[T]3．一个质点的角动量与参考点的选择有关。

解：p r L ⨯=，其中r与参考点的选择密切相关，所以角动量与参考点的选择有关。

[F]4．刚体的转动惯量反映了刚体转动的惯性大小，对确定的刚体，其转动惯量是一定值。

解：转动惯量还与轴的位置有关系，该题目只说了刚体确定，但没有说是定轴。

该题题意有些含混。

[F ]5．如果作用于质点的合力矩垂直于质点的角动量，则质点的角动量将不发生变化。

解：根据,,L L d L M dtL d M⊥⊥=，即是如果只要一个物理量的增量垂直于它本身，那么这个增量就只改变它的方向，不改变它的大小。

比如旋进。

二、选择题:1．有两个半径相同、质量相等的细圆环A 和B 。

A 环的质量分布均匀，B 环的质量分布不均匀。

它们对通过环心并与环面垂直的轴的转动惯量分别为A J 和B J ，则[C ](A)A J >B J (B)A J <BJ (C)A J =BJ (D)不能确定A J 、BJ 哪个大解：对于圆环，转动惯量为⎰⎰==m R m r J d d 22，设细圆环总质量为M ，无论质量分布均匀与否，都有M m =⎰d ，所以MR J JB A2==选CRO2．绕定轴转动的刚体转动时,如果它的角速度很大,则[D ](A)作用在刚体上的力一定很大(B)作用在刚体上的外力矩一定很大(C)作用在刚体上的力和力矩都很大(D)难以判断外力和力矩的大小3．一个可绕定轴转动的刚体,若受到两个大小相等、方向相反但不在一条直线上的恒力作用,而且力所在的平面不与转轴平行,刚体将怎样运动?[C ](A)静止(B)匀速转动(C)匀加速转动(D)变加速转动解：对轴的力矩的代数和不为0，并且为恒定值，根据转动定律：恒量恒量=⇒==ββJ M Z ，所以是匀加速的转动，选C 。

大学物理西南交大作业参考答案公司内部档案编码：[OPPTR-OPPT28-OPPTL98-OPPNN08]电势、导体与※电介质中的静电场 （参考答案）班级： 学号： 姓名： 成绩： 一 选择题1．真空中一半径为R 的球面均匀带电Q ，在球心O 处有一带电量为q 的点电荷，如图所示，设无穷远处为电势零点，则在球内离球心O 距离为r 的P 点处的电势为：（A ）r q04πε； （B ）)(041R Qrq +πε； （C ）rQq 04πε+； （D ）)(041R qQ rq -+πε；参考：电势叠加原理。

[ B ]2．在带电量为-Q 的点电荷A 的静电场中，将另一带电量为q 的点电荷B 从a 点移动到b ，a 、b 两点距离点电荷A 的距离分别为r 1和r 2，如图，则移动过程中电场力做功为：（A ）)(210114r r Q --πε； （B ）)(21114r r qQ-πε；（C ）)(210114r r qQ--πε； （D ）)(4120r r qQ --πε。

参考：电场力做功＝势能的减小量。

A=W a -W b ＝q(U a -U b ) 。

[ C ]3点，有人（A ）电场强度E M ＜E N ； （B ）电势U M ＜U N ； （C ）电势能W M ＜W N ； （D ）电场力的功A ＞0。

r 2 (-br 1B a（q[ C ]4．一个未带电的空腔导体球壳内半径为R ，在腔内离球心距离为d （d ＜R ）处，固定一电量为+q 的点电荷，用导线把球壳接地后，再把地线撤去，选无穷远处为电势零点，则球心O 处的点势为： （A ）0； （B ）d q04πε； （C ）-R q04πε； （D ）)(1140R dq-πε。

外表面无电荷（可分析）。

虽然内表面电荷分布不均，但到O 点的距离相同，故由电势叠加原理可得。

[ D ]※5．在半径为R 的球的介质球心处有电荷+Q ，在球面上均匀分布电荷-Q ，则在球内外处的电势分别为： （A ）内r Q πε4+，外r Q 04πε-； （B ）内r Qπε4+，0； 参考：电势叠加原理。

大学物理西南交大作业参考答案公司内部档案编码：[OPPTR-OPPT28-OPPTL98-OPPNN08]电势、导体与※电介质中的静电场 （参考答案）班级： 学号： 姓名： 成绩： 一 选择题1．真空中一半径为R 的球面均匀带电Q ，在球心O 处有一带电量为q 的点电荷，如图所示，设无穷远处为电势零点，则在球内离球心O 距离为r 的P 点处的电势为：（A ）r q04πε； （B ）)(041R Qrq +πε； （C ）rQq 04πε+； （D ）)(041R qQ rq -+πε；参考：电势叠加原理。

[ B ]2．在带电量为-Q 的点电荷A 的静电场中，将另一带电量为q 的点电荷B 从a 点移动到b ，a 、b 两点距离点电荷A 的距离分别为r 1和r 2，如图，则移动过程中电场力做功为：（A ）)(210114r r Q --πε； （B ）)(21114r r qQ-πε；（C ）)(210114r r qQ--πε； （D ）)(4120r r qQ --πε。

参考：电场力做功＝势能的减小量。

A=W a -W b ＝q(U a -U b ) 。

[ C ]3点，有人（A ）电场强度E M ＜E N ； （B ）电势U M ＜U N ； （C ）电势能W M ＜W N ； （D ）电场力的功A ＞0。

r 2 (-br 1B a（q[ C ]4．一个未带电的空腔导体球壳内半径为R ，在腔内离球心距离为d （d ＜R ）处，固定一电量为+q 的点电荷，用导线把球壳接地后，再把地线撤去，选无穷远处为电势零点，则球心O 处的点势为： （A ）0； （B ）d q04πε； （C ）-R q04πε； （D ）)(1140R dq-πε。

外表面无电荷（可分析）。

虽然内表面电荷分布不均，但到O 点的距离相同，故由电势叠加原理可得。

[ D ]※5．在半径为R 的球的介质球心处有电荷+Q ，在球面上均匀分布电荷-Q ，则在球内外处的电势分别为： （A ）内r Q πε4+，外r Q 04πε-； （B ）内r Qπε4+，0； 参考：电势叠加原理。

©物理系_2015_09《大学物理CII》作业No.7 热力学第二定律班级________ 学号________ 姓名_________ 成绩_______一、判断题：（用“T”和“F”表示）[ F ] 1．在任意的绝热过程中，只要系统与外界之间没有热量传递，系统的温度就不会发生变化。

此说法不对．在绝热过程中，系统与外界无热量交换，Q=0．但不一定系统与外界无作功，只要系统与外界之间有作功的表现，由热力学第一定律Q=E+W，可知，E=-W，即对应有内能的改变．而由E=νC，T可知，有E，一定有T，即有温度的变化．[ F ] 2．在循坏过程中系统对外做的净功在数值上等于p-V图中封闭曲线所包围的面积，因此封闭曲线包围的面积越大，循坏效率就越高。

有人说，因为在循环过程中系统对外做的净功在数值等于p-V图中封闭曲线所包围的面积，所以封闭曲线所包围的面积越大，循环效率就越高，对吗？答：不正确，因为循环效率取决于系统对外做的净功和系统由高温热源吸收的热量，只有在从高温热源吸收的热量一定的情况下，封闭曲线所包围的面积越大，即系统对外所做的净功越多，循环效率越高，如果从高温热源吸收的热量不确定，则循环效率不一定越高[ F ] 3．系统经历一正循坏后，系统与外界都没有变化。

系统经历一正循环后，系统的状态没有变化；（２）系统经历一正循环后，系统与外界都没有变化；（３）系统经历一正循环后，接着再经历一逆循环，系统与外界亦均无变化。

解说法（1）正确，系统经历一正循环后，描述系统状态的内能是单值函数，其内能不变，系统的状态没有变化。

说法（2）错误，系统经过一正循环，系统内能不变，它从外界吸收热量，对外作功，由热力学第二定律知，必定要引起外界的变化。

说法（3）错误，在正逆过程中所引起外界的变化是不能消除的。

[ F ] 4.第二类永动机不可能制成是因为违背了能量守恒定律。

解：第二类永动机并不违背能量守恒定律，但它违背了热力学第二定律。

第五章 角动量 角动量守恒定律5-1 选择题：（1）一质点作匀速率圆周运动时，（A ）它的动量不变，对圆心的角动量也不变。

（B ）它的动量不变，对圆心的角动量不断改变。

（C ）它的动量不断改变，对圆心的角动量不变。

（D ）它的动量不断改变，对圆心的角动量也不断改变。

[C] 解：质点作匀速率圆周运动时，其速度大小虽不变，但速度方向不断改变，故其动量不断改变。

而该质点对圆心角动量大小不变，方向始终垂直于圆轨道平面，指向也不变。

（2）已知地球的质量为m ，太阳的质量为M ，地心与日心的距离为R ，引力常数为G ，则地球绕太阳作圆周运动的轨道角动量为（A ）GMR m （B ）RGMm（C ）R G Mm（D ）RGMm 2 [A] 解：由万有引力定律和牛顿第二定律有R v m RmM G 22=得地球绕日运动速率RGM v =由角动量定义得GMR m mvR L ==（3）一刚体以每分钟60转绕Z 轴做匀速转动（ω沿z 轴正方向），设某时刻刚体上一点P 的位置矢量为k j i r 543++=，其单位为“m 102-”，若以“12s m 10--⋅”为速度单位，则该时刻P 点的速度为：（A ）k j i v 0.1576.1252.94++= （B ）j i v 8.181.25+-= （C ）j i v 8.181.25--=（D ）k v 4.31= [B] 解：刚体转动平面与转轴垂直，所以P 点速度无z 分量。

由题意，作出P 的位矢，可知该时刻P 点速度的x 分量为负而y 分量为正，故答案（B ）正确。

（4）均匀细棒OA 可绕通过其一端O 而与棒垂直的水平固定光滑轴转动，如图所示，今使棒从水平位置由静止开始自由下落，在棒摆动到竖直位置的过程中，下述说法哪一种是正确的？（A ）角速度从小到大，角加速度从大到小。

（B ）角速度从小到大，角加速度从小到大。

（C ）角速度从大到小，角加速度从大到小。

《大学物理》作业No.1 运动的描述一、选择题1. 一小球沿斜面向上运动，其运动方程为245t t s -+=(SI)，则小球运动到最高点的时刻是[ B ] (A) s 4=t ; (B) s 2=t ; (C) s 8=t ; (D) s 5=t 。

解：小球运动速度t tsv 24d d -==。

当小球运动到最高点时0=v ，即024=-t ，t = 2(s)。

2. 质点作半径为R 的变速圆周运动时的加速度大小为(v 表示任意时刻质点的速率)[ D ] (A)tvd d(B) R v 2(C)Rv t v 2d d + (D)⎪⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛242d d R v t v 解：质点作圆周运动时，切向加速度和法向加速度分别为Rv a t v a n t 2,d d ==，所以加速度大小为：22222d d ⎪⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛=+=R v t v a a a n t 。

3. 一质点在平面上作一般曲线运动，其瞬时速度为v，瞬时速率为v ，某一段时间内的平均速度为v，平均速率为v ，它们之间的关系必定有[ D ] (A) v v v v == , (B) v v v v =≠,(C) v v v v ≠≠ , (D) v v v v ≠= ,解：根据定义，瞬时速度为t r v d d=，瞬时速率为ts v d d =，由于s r d d = ，所以v v =。

平均速度t r v ∆∆=，平均速率ts v ∆∆=，由于一般情况下s r ∆≠∆，所以v v ≠ 。

4. 某物体的运动规律为t kv tv2d d -=，式中的k 为大于零的常数。

当t ＝0时，初速为0v ，则速度v 与t 的函数关系是[ C ] (A) 0221v kt v +=(B) 0221v kt v +-=(C) 02121v kt v +=(D) 02121v kt v +-= 解：将t kv tv 2d d -=分离变量积分，⎰⎰=-t v v t kt v v 02d d 0可得 02201211,2111v kt v kt v v +==-。