平面直角坐标系知识结构图

七年级下册数学知识点归纳TYYGROUP system office room 【TYYUA16H-TYY-TYYYUA8Q8-七年级下册第五章相交线与平行线一、知识结构图相交线相交线垂线同位角、内错角、同旁内角平行线平行线及其判定平行线的判定平行线的性质平移命题、定理二、知识定义邻补角：两条直线相交所构成的四个角中，有公共顶点且有一条公共边的两个角是邻补角。

对顶角：一个角的两边分别是另一个叫的两边的反向延长线，像这样的两个角互为对顶角。

垂线：两条直线相交成直角时，叫做互相垂直，其中一条叫做另一条的垂线。

平行线：在同一平面内，不相交的两条直线叫做平行线。

同位角、内错角、同旁内角：同位角：∠1与∠5像这样具有相同位置关系的一对角叫做同位角。

内错角：∠2与∠6像这样的一对角叫做内错角。

同旁内角：∠2与∠5像这样的一对角叫做同旁内角。

命题：判断一件事情的语句叫命题。

平移：在平面内，将一个图形沿某个方向移动一定的距离，图形的这种移动叫做平移平移变换，简称平移。

对应点：平移后得到的新图形中每一点，都是由原图形中的某一点移动后得到的，这样的两个点叫做对应点。

三、定理与性质对顶角的性质：对顶角相等。

垂线的性质：性质1：过一点有且只有一条直线与已知直线垂直。

性质2：连接直线外一点与直线上各点的所有线段中，垂线段最短。

平行公理：经过直线外一点有且只有一条直线与已知直线平行。

平行公理的推论：如果两条直线都与第三条直线平行，那么这两条直线也互相平行。

平行线的性质：性质1：两直线平行，同位角相等。

性质2：两直线平行，内错角相等。

性质3：两直线平行，同旁内角互补。

平行线的判定：判定1：同位角相等，两直线平行。

判定2：内错角相等，两直线平行。

判定3：同旁内角相等，两直线平行。

第六章实数【自然数】表示物体个数的1、2、3、4?等都称为自然数【质数与合数】一个大于1的整数，如果除了它本身和1以外不能被其它正整数所整除，那么这个数称为质数。

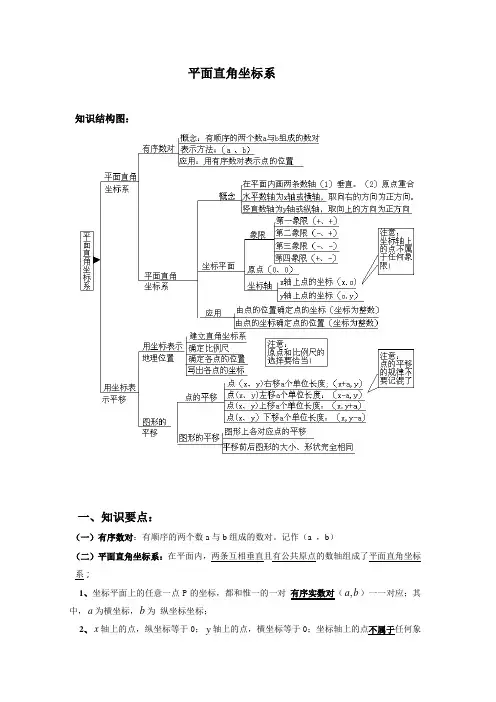
平面直角坐标系知识结构图：一、知识要点：（一）有序数对：有顺序的两个数a与b组成的数对。

记作（a ，b）（二）平面直角坐标系：在平面内，两条互相垂直且有公共原点的数轴组成了平面直角坐标系；a,）一一对应；其1、坐标平面上的任意一点P的坐标，都和惟一的一对有序实数对（b中，a为横坐标，b为纵坐标坐标；2、x轴上的点，纵坐标等于0；y轴上的点，横坐标等于0；坐标轴上的点不属于任何象限（三）四个象限的点的坐标具有如下特征：1、点P （y x ,）所在的象限 横、纵坐标x 、y 的取值的正负性；2、点P （y x ,）所在的数轴 横、纵坐标x 、y 中必有一数为零； （四）在平面直角坐标系中，已知点P ),(b a ，则 1、点P 到x 轴的距离为b ； 2、点P 到y 轴的距离为a ；3、点P 到原点O 的距离为PO ＝ 22b a +（五）平行直线上的点的坐标特征：1、在与x 轴平行的直线上， 所有点的纵坐标相等；点A 、B 的纵坐标都等于m ；2、在与y 轴平行的直线上，所有点的横坐标相等；点C 、D 的横坐标都等于n ；（六）对称点的坐标特征：1、点P ),(n m 关于x 轴的对称点为),(1n m P -， 即横坐标不变，纵坐标互为相反数；象限 横坐标x纵坐标y第一象限 正 正 第二象限 负 正 第三象限 负 负 第四象限正负P （b a ,）abxy OXYA BmXYC Dn2、点P ),(n m 关于y 轴的对称点为),(2n m P -， 即纵坐标不变，横坐标互为相反数；3、点P ),(n m 关于原点的对称点为),(3n m P --，即横、纵坐标都互为相反数；关于x 轴对称 关于y 轴对称 关于原点对称（七）两条坐标轴夹角平分线上的点的坐标的特征：1、若点P （n m ,）在第一、三象限的角平分线上，则n m =，即横、纵坐标相等；2、若点P （n m ,）在第二、四象限的角平分线上，则n m -=，即横、纵坐标互为相反数；在第一、三象限的角平分线上 在第二、四象限的角平分线上（八）利用平面直角坐标系绘制区域内一些点分布情况平面图过程如下：1、建立坐标系，选择一个适当的参照点为原点，确定x 轴、y 轴的正方向；2、根据具体问题确定适当的比例尺，在坐标轴上标出单位长度；3、在坐标平面内画出这些点，写出各点的坐标和各个地点的名称。

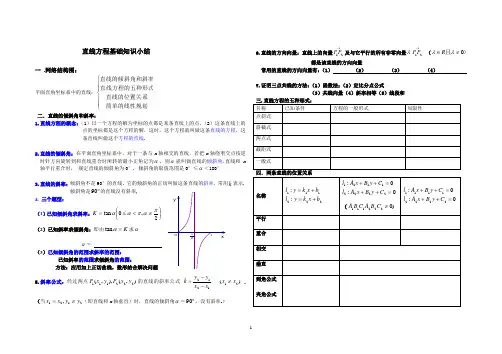
直线方程基础知识小结一 .网络结构图：平面直角坐标系中的直线：⎪⎪⎩⎪⎪⎨⎧简单的线性规划直线的位置关系直线方程的五种形式直线的倾斜角和斜率二．直线的倾斜角和斜率：1.直线方程的概念：（1，这条直线叫做这个方程的直线.2.直线的倾斜角：在平面直角坐标系中，对于一条与x 时针方向旋转到和直线重合时所转的最小正角记为αx 轴平行重合时， 规定直线的倾斜角为0°.3.直线的斜率：倾斜角不是90°的直线，k 表示.倾斜角是︒90的直线没有斜率4. 三个题型： （1）已知倾斜角求斜率：⎪⎭⎫ ⎝⎛≠<≤=2,0tan παπααK （2）已知斜率求倾斜角：即由K =αtan 求αα＝（3）已知倾斜角的范围求斜率的范围：已知斜率的范围求倾斜角的范围：方法：应用如上正切曲线，数形结合解决问题5.斜率公式：经过两点),(),,(222111y x P y x P )2x ≠（当2121,y y x x ≠=（即直线和x6.直线的方向向量：直线上的向量→21P P 及与它平行的所有非零向量λ→21P P （）且0≠∈λλR 都是该直线的方向向量 常用的直线的方向向量有：（1） （2） （3） （4）7.证明三点共线的方法：（1）函数法；（2）定比分点公式（3）共线向量（4）斜率相等（5）线段和五．点到直线的距离公式：（1）P ()00,y x 到直线0:=++C By Ax l 的距离公式：（2）0:;0:2211=++=++C By Ax l C By Ax l 的距离公式：（3）P ()00,y x 到直线a x l =:的距离公式：P ()00,y x 到直线b y l =:的距离公式： 六．直线的对称问题：1．点关于点的对称点问题：()()())2,2(),(,,00y b x a y x y x ba ----任意点，坐标原点关于方法依据：中点坐标公式 2. 点关于直线的对称点问题：()()()()()()()()()(),,0,,,,2,,2,,=++=+-=++-=====-=+----------C By Ax c y x c y x xy xy by ax y y x x c x c y c x c y x y x y y b x y x a y x y x 直线直线直线直线直线直线直线直线直线关于说明：01（1）到（4）方法依据是中点坐标公式02（5）到（9）方法依据是：点关于直线对称点的基本解法3点关于直线对称的基本解法：直接法：设所求的对称点坐标是（),00y x 则由题意有：⎪⎪⎩⎪⎪⎨⎧-=-⨯--=++++1)(0220000B A x x y y C y y B xx A ⎩⎨⎧==∴00y x间接法 ：3.三个典型题：（1）距离和的最小值问题：在定直线l 上取点P ，求P 到两定点A,B 距离和PB PA +的最小值当两定点A,B 在直线l 的两侧时：PB PA +AB ≥，最小值是,AB 此时点P 坐标由方程组⎩⎨⎧=++:0:AB l C By Ax l 决定 当两定点A,B 在直线l 的同侧时：先求点B 关于定直线l 的对称点 /B ，则PB PA +＝//AB PB PA ≥+，最小值是/AB此时点P 坐标由方程组 ⎩⎨⎧=++:0:/AB l C By Ax l 决定 （2）距离差的最大值问题：在定直线l 上取点P ，求P 到两定点A,B 距离差PB PA -的最大值当两定点A,B 在直线l 的同侧时：PB PA -AB ≥，最大值是,AB 此时点P 坐标由方程组⎩⎨⎧=++:0:AB l C By Ax l 决定 当两定点A,B 在直线l 的两侧时：先求点B 关于定直线l 的对称点 /B ，PB PA -＝//AB PB PA ≤- ，最大值是,AB 此时点P 坐标由方程组⎩⎨⎧=++:0:/AB l C By Ax l 决定（3）入射光线和反射光线问题：入射光线上的点关于界面的对称点在反射光线上；反射光线上的点关于界面的对称点在入射光线上； 入射光线与界面的交点在反射光线上； 反射光线与界面的交点在入射光线上；界面是x 轴（y 轴）时，考虑入射光线与反射光线的斜率互为相反数； 界面是直线y=x(y=-x)时，考虑入射光线与反射光线上点的对称 例5光线由点)4,1(-A 射出，遇到直线l ：0632=-+y x 后被反射，已知其)1362,3(B ， 求反射光线所在直线的方程.七.几组特殊的直线系方程：1.直线系方程的定义：具有某种共同性质(过某点、共斜率等)的所有直线的集合叫做直线系。

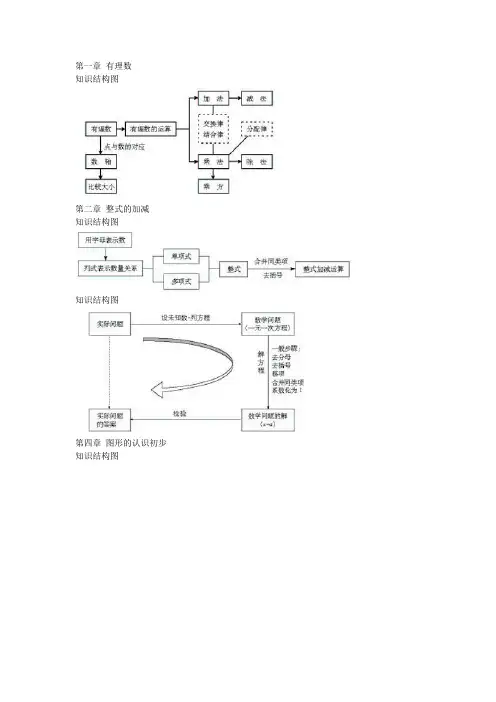
初中数学知识点及结构图2 -七年级数学（上）知识点人教版七年级数学上册主要包含了有理数、整式的加减、一元一次方程、图形的认识初步四个章节的内容.第一章 有理数一． 知识框架二．知识概念1.有理数：(1)凡能写成)0p q ,p (pq 为整数且形式的数，都是有理数.正整数、0、负整数统称整数；正分数、负分数统称分数；整数和分数统称有理数.注意：0即3 -4 -(2) 绝对值可表示为：⎪⎩⎪⎨⎧<-=>=)0a (a )0a (0)0a (a a 或⎩⎨⎧<-≥=)0a (a )0a (a a ；绝对值的问题经常分类讨论；5.有理数比大小：（1）正数的绝对值越大，这个数越大；（2）正数永远比0大，负数永远比0小；（3）正数大于一切负数；（4）两个负数比大小，绝对值大的反而小；（5）数轴上的两个数，右边的数总比左边的数大；（6）大数-小数 ＞ 0，小数-大数 ＜ 0.6.互为倒数：乘积为1的两个数互为倒数；注意：0没有倒数；若 a ≠0，那么a 的倒数是a1；若ab=1⇔ a 、b 互为倒数；若ab=-1⇔ a 、b 互为负倒数.7. 有理数加法法则：（1）同号两数相加，取相同的符号，并把绝对值相加；（2）异号两数相加，取绝对值较大的符号，并用较大的绝对值减去较小的绝对值；（3）一个数与0相加，仍得这个数.8．有理数加法的运算律：（1）加法的交换律：a+b=b+a ；（2）加法的结合律：（a+b）+c=a+（b+c）.9．有理数减法法则：减去一个数，等于加上这个数的相反数；即a-b=a+（-b）.10 有理数乘法法则：（1）两数相乘，同号为正，异号为负，并把绝对值相乘；（2）任何数同零相乘都得零；（3）几个数相乘，有一个因式为零，积为零；各个因式都不为零，积的符号由负因式的个数决定.11 有理数乘法的运算律：（1）乘法的交换律：ab=ba；（2）乘法的结合律：（ab）c=a（bc）；（3）乘法的分配律：a（b+c）=ab+ac .5 -12．有理数除法法则：除以一个数等于乘以这个数的倒数；注意：零不能做除数，无意义a.即13．有理数乘方的法则：（1）正数的任何次幂都是正数；（2）负数的奇次幂是负数；负数的偶次幂是正数；注意：当n为正奇数时: (-a)n=-a n或(a -b)n=-(b-a)n, 当n为正偶数时: (-a)n=a n 或(a-b)n=(b-a)n .14．乘方的定义：（1）求相同因式积的运算，叫做乘方；（2）乘方中，相同的因式叫做底数，相同因式的个数叫做指数，乘方的结果叫做幂；15．科学记数法：把一个大于10的数记成a×10n的形式，其中a是整数数位只有一位的数，这种记数法叫科学记数法.16.近似数的精确位：一个近似数，四舍五入到那一位，就说这个近似数的精确到那一位.6 -17.有效数字：从左边第一个不为零的数字起，到精确的位数止，所有数字，都叫这个近似数的有效数字.18.混合运算法则：先乘方，后乘除，最后加减.本章内容要求学生正确认识有理数的概念，在实际生活和学习数轴的基础上，理解正负数、相反数、绝对值的意义所在。

1 -七年级数学（上）知识点人教版七年级数学上册主要包含了有理数、整式的加减、一元一次方程、图形的认识初步四个章节的内容.第一章 有理数一． 知识框架二．知识概念1.有理数：(1)凡能写成)0p q ,p (pq ≠为整数且形式的数，都是有理数.正整数、0、负整数统称整数；正分数、负分数统称分数；整数和分数统称有理数.注意：0即不是正数，也不是负数；-a 不一定是负数，+a 也不一定是正数；π不是有理数；(2)有理数的分类: ① ⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧⎩⎨⎧负分数负整数负有理数零正分数正整数正有理数有理数 ② ⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧⎪⎩⎪⎨⎧负分数正分数分数负整数零正整数整数有理数2．数轴：数轴是规定了原点、正方向、单位长度的一条直线.3．相反数：(1)只有符号不同的两个数，我们说其中一个是另一个的相反数；0的相反数还是0；(2)相反数的和为0 ⇔ a+b=0 ⇔ a 、b 互为相反数.4.绝对值：(1)正数的绝对值是其本身，0的绝对值是0，负数的绝对值是它的相反数；注意：绝对值的意义是数轴上表示某数的点离开原点的距离；(2) 绝对值可表示为：⎪⎩⎪⎨⎧<-=>=)0a (a )0a (0)0a (a a 或⎩⎨⎧<-≥=)0a (a )0a (a a ；绝对值的问题经常分类讨论； 5.有理数比大小：（1）正数的绝对值越大，这个数越大；（2）正数永远比0大，负数永远比0小；（3）正数大于一切负数；（4）两个负数比大小，绝对值大的反而小；（5）数轴上的两个数，右边的数总比左边的数大；（6）大数-小数 ＞ 0，小数-大数 ＜ 0.6.互为倒数：乘积为1的两个数互为倒数；注意：0没有倒数；若 a ≠0，那么a 的倒数是a1；若ab=1⇔ a 、b 互为倒数；若ab=-1⇔ a 、b 互为负倒数.7. 有理数加法法则：（1）同号两数相加，取相同的符号，并把绝对值相加；（2）异号两数相加，取绝对值较大的符号，并用较大的绝对值减去较小的绝对值；（3）一个数与0相加，仍得这个数.8．有理数加法的运算律：（1）加法的交换律：a+b=b+a ；（2）加法的结合律：（a+b ）+c=a+（b+c ）.9．有理数减法法则：减去一个数，等于加上这个数的相反数；即a-b=a+（-b ）.2 -10 有理数乘法法则：（1）两数相乘，同号为正，异号为负，并把绝对值相乘；（2）任何数同零相乘都得零；（3）几个数相乘，有一个因式为零，积为零；各个因式都不为零，积的符号由负因式的个数决定.11 有理数乘法的运算律：（1）乘法的交换律：ab=ba ；（2）乘法的结合律：（ab ）c=a （bc ）；（3）乘法的分配律：a （b+c ）=ab+ac .12．有理数除法法则：除以一个数等于乘以这个数的倒数；注意：零不能做除数，无意义即0a .13．有理数乘方的法则：（1）正数的任何次幂都是正数；（2）负数的奇次幂是负数；负数的偶次幂是正数；注意：当n 为正奇数时: (-a)n =-a n 或(a -b)n =-(b-a)n , 当n为正偶数时: (-a)n =a n 或 (a-b)n =(b-a)n .14．乘方的定义：（1）求相同因式积的运算，叫做乘方；（2）乘方中，相同的因式叫做底数，相同因式的个数叫做指数，乘方的结果叫做幂；15．科学记数法：把一个大于10的数记成a ×10n 的形式，其中a 是整数数位只有一位的数，这种记数法叫科学记数法.16.近似数的精确位：一个近似数，四舍五入到那一位，就说这个近似数的精确到那一位.17.有效数字：从左边第一个不为零的数字起，到精确的位数止，所有数字，都叫这个近似数的有效数字.18.混合运算法则：先乘方，后乘除，最后加减.本章内容要求学生正确认识有理数的概念，在实际生活和学习数轴的基础上，理解正负数、相反数、绝对值的意义所在。

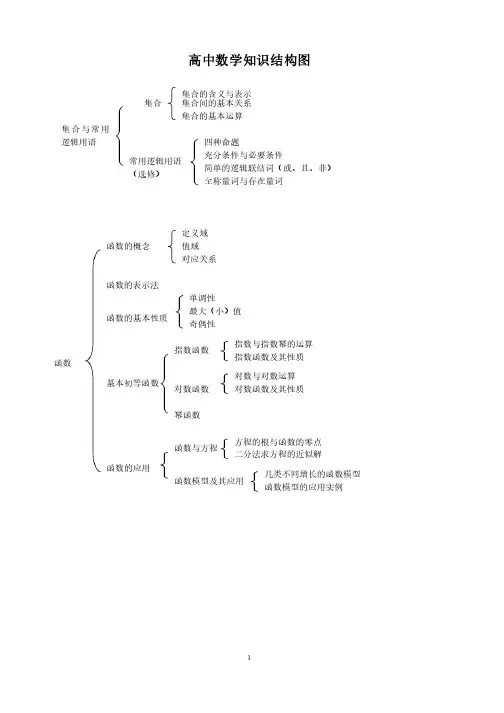
高中数学知识结构图与集合与常常用逻辑用语逻辑用语集合集合集合的含义与表示集合的含义与表示集合间的基本关系集合间的基本关系 集合的基本运算集合的基本运算常用逻辑用语常用逻辑用语（选修）（选修）四种命题四种命题充分条件与必要条件充分条件与必要条件简单的逻辑联结词（或、且、非）简单的逻辑联结词（或、且、非） 全称量词与存在量词全称量词与存在量词函数函数函数的概念函数的概念函数的表示法函数的表示法函数的基本性质函数的基本性质基本初等函数基本初等函数函数的应用函数的应用定义域定义域值域值域 对应关系对应关系单调性单调性最大（小）值最大（小）值 奇偶性奇偶性 指数函数指数函数对数函数对数函数幂函数幂函数指数与指数幂的运算指数与指数幂的运算指数函数及其性质指数函数及其性质 对数与对数运算对数与对数运算 对数函数及其性质对数函数及其性质函数与方程函数与方程函数模型及其应用函数模型及其应用方程的根与函数的零点方程的根与函数的零点二分法求方程的近似解二分法求方程的近似解几类不同增长的函数模型几类不同增长的函数模型函数模型的应用实例函数模型的应用实例立体几何立体几何 空间几何体空间几何体点、直线、平面点、直线、平面之间的位置关系之间的位置关系空间几何体的结构空间几何体的结构空间几何体的三视图和直观图空间几何体的三视图和直观图空间几何体的表面积与体积空间几何体的表面积与体积直线、平面平行的判定及其性质直线、平面平行的判定及其性质柱、锥、台、球的结构特征柱、锥、台、球的结构特征 简单组合体的结构特征简单组合体的结构特征柱、锥、台的表面积与体积柱、锥、台的表面积与体积球的体积和表面积球的体积和表面积平面及其性质（三个公理）平面及其性质（三个公理） 空间直线与直线之间的位置关系空间直线与直线之间的位置关系空间中直线与平面之间的位置关系空间中直线与平面之间的位置关系 平面与平面之间的位置关系平面与平面之间的位置关系空间点、直线、平面之间空间点、直线、平面之间的位置关系的位置关系直线、平面垂直的判定及其性质直线、平面垂直的判定及其性质直线与平面平行的判定直线与平面平行的判定平面与平面平行的判定平面与平面平行的判定 直线与平面平行的性质直线与平面平行的性质 平面与平面平行的性质平面与平面平行的性质 直线与平面垂直的判定直线与平面垂直的判定 平面与平面垂直的判定平面与平面垂直的判定 直线与平面垂直的性质平面与平面垂直的性质面与平面垂直的性质直线与圆直线与圆直线与方程直线与方程圆与方程圆与方程 直线的倾斜角和斜率直线的倾斜角和斜率直线的方程直线的方程直线的交点坐标与距离公式直线的交点坐标与距离公式直线、圆的位置关系直线、圆的位置关系倾斜角与斜率倾斜角与斜率两条直线平行与垂直的判定两条直线平行与垂直的判定直线的点斜式方程（含斜截式方程） 直线的两点式方程（含截距式方程） 直线的一般式方程直线的一般式方程 圆的标准方程圆的标准方程圆的一般方程圆的一般方程圆的方程圆的方程空间直角坐标系空间直角坐标系两条直线的交点坐标两条直线的交点坐标两点间的距离两点间的距离 点到直线的距离点到直线的距离两条平行直线间的距离两条平行直线间的距离直线与圆的位置关系直线与圆的位置关系圆与圆的位置关系圆与圆的位置关系 直线与圆的方程的应用直线与圆的方程的应用空间直角坐标系空间直角坐标系空间两点间的距离公式空间两点间的距离公式算法初步算法初步概率与统计概率与统计 统计案例统计案例算法与程序框图算法与程序框图基本算法语句基本算法语句算法案例算法案例算法的概念算法的概念程序框图与算法的基本逻辑结构程序框图与算法的基本逻辑结构 输入语句、输出语句和赋值语句输入语句、输出语句和赋值语句条件语句条件语句 循环语句循环语句随机抽样随机抽样统计统计概率概率求最大公约数（辗转相除法、更相减损术） 秦九韶算法秦九韶算法 进位制进位制简单随机抽样简单随机抽样系统抽样系统抽样 分层抽样分层抽样用样本估计总体用样本估计总体用样本的频率分布估计总体分布用样本的频率分布估计总体分布 用样本的数字特征估计总体的数字特征用样本的数字特征估计总体的数字特征变量间的相关关系变量间的相关关系变量之间的相关关系变量之间的相关关系两个变量的线性相关（线性回归方程）两个变量的线性相关（线性回归方程）随机事件的概率随机事件的概率 古典概型古典概型 几何概型几何概型随机事件的概率随机事件的概率概率的意义概率的意义概率的基本性质概率的基本性质统计案例统计案例（选修）（选修）独立性检验独立性检验回归分析回归分析离散型随机变量离散型随机变量分布列分布列 期望期望 方差方差两点分布两点分布二项分布二项分布 超几何分布超几何分布 正态分布正态分布正态分布密度曲线正态分布密度曲线 3σ分布σ分布条件概率和事件的独立性条件概率和事件的独立性独立事件同时发生的概率独立事件同时发生的概率独立重复试验独立重复试验三角函数三角函数 任意角和弧度制任意角和弧度制三角函数三角函数三角恒等变换三角恒等变换任意角的三角函数与同角三角函数的基本关系任意角的三角函数与同角三角函数的基本关系 三角函数的诱导公式三角函数的诱导公式 平方关系平方关系商数关系商数关系三角函数的图象与性质三角函数的图象与性质正弦函数、余弦函数的图象正弦函数、余弦函数的图象正弦函数、余弦函数的性质正弦函数、余弦函数的性质 正切函数的性质与图象正切函数的性质与图象函数y ＝Asin （ωx ＋φ）的图象）的图象 三角函数模型的简单应用三角函数模型的简单应用两角和与差的正弦、两角和与差的正弦、余弦、正切公式余弦、正切公式余弦、正切公式二倍角的正弦、余弦、正切公式二倍角的正弦、余弦、正切公式解三角形解三角形正弦定理正弦定理 余弦定理余弦定理向量向量平面向量的实际背景及基本概念平面向量的实际背景及基本概念平面向量平面向量平面向量应用平面向量的线性运算平面向量的线性运算向量加法运算及其几何意义向量加法运算及其几何意义向量减法运算及其几何意义向量减法运算及其几何意义 向量数乘运算及其几何意义向量数乘运算及其几何意义平面向量的基本定理及坐标表示平面向量的基本定理及坐标表示平面向量的数量积平面向量的数量积平面向量数量积的物理背景及其含义平面向量数量积的物理背景及其含义平面向量数量积的坐标表示、模、夹角平面向量数量积的坐标表示、模、夹角空间向量空间向量（选修）（选修）空间向量及其运算空间向量及其运算立体几何中的向量方法立体几何中的向量方法向量的物理背景与概念向量的物理背景与概念向量的几何表示向量的几何表示 相等向量与共线向量相等向量与共线向量平面向量基本定理平面向量基本定理平面向量的正交分解及坐标表示平面向量的正交分解及坐标表示 平面向量的坐标运算平面向量的坐标运算 平面向量共线的坐标表示平面向量共线的坐标表示平面几何中的向量方法平面几何中的向量方法 向量在物理中的应用举例向量在物理中的应用举例空间向量的直角坐标运算空间向量的直角坐标运算空间向量的数量积空间向量的数量积 空间向量的基本定理空间向量的基本定理 空间向量的线性运算空间向量的线性运算数列的概念与简单表示法数列的概念与简单表示法数列数列等比数列的前n 项和项和 等差数列等差数列等差数列的前n 项和项和等比数列等比数列数列的应用数列的应用不等关系与不等式不等关系与不等式不等式不等式 不等式选讲不等式选讲一元二次不等式及其解法一元二次不等式及其解法二元一次不等式（组）与简单的线性基本不等式2a bab +≤基本性质基本性质比较大小比较大小二元一次不等式(组)与平面区域与平面区域简单的线性规划问题简单的线性规划问题不等式与绝对值不等式不等式与绝对值不等式柯西不等式柯西不等式 数学归纳法数学归纳法不等式证明的基本方法不等式证明的基本方法比较法、综合法、分析法比较法、综合法、分析法反证法、放缩法反证法、放缩法复数的基本概念复数的基本概念复数代数形式的四则运算复数代数形式的四则运算复数(选修)变化率与导数变化率与导数几种常见函数的导数几种常见函数的导数 导数的运算导数的运算导数在研究函数中的应用导数在研究函数中的应用 生活中的优化问题举例生活中的优化问题举例 定积分的概念定积分的概念 微积分基本定理微积分基本定理椭圆及其标准方程椭圆及其标准方程 椭圆的简单性质椭圆的简单性质双曲线的标准方程和简单性质双曲线的标准方程和简单性质 抛物线及其标准方程抛物线及其标准方程 抛物线的简单性质抛物线的简单性质直线与圆锥曲线的位置关系直线与圆锥曲线的位置关系 圆锥曲线的简单应用圆锥曲线的简单应用平面直角坐标系伸缩变换下的平面图形变化平面直角坐标系伸缩变换下的平面图形变化极坐标系极坐标系极坐标系中简单图形的方程极坐标系中简单图形的方程 柱坐标系、球坐标系简介柱坐标系、球坐标系简介计数原理、二项式定理计数原理、二项式定理分类计数原理和分步计数原理分类计数原理和分步计数原理排列排列 组合组合二项式定理二项式定理坐标系参数方程抛物运动轨迹的参数方程抛物运动轨迹的参数方程直线、圆和圆锥曲线的参数方程直线、圆和圆锥曲线的参数方程 参数方程与普通方程的比较参数方程与普通方程的比较 平摆线和渐开线的参数方程平摆线和渐开线的参数方程优选法与试验设计初步优选法优选法试验设计初步试验设计初步。

初中数学知识构造图1.有理数（正数与负数）2.数轴6.有理数的见解 3.相反数4.绝对值5.有理数从大到小比较7.有理数的加法、加法运算律17.有理数8.有理数的减法9.有理数的加减混和运算10.有理数的乘法、乘法运算16.有理数的运算11.有理数的除法、倒数12.有理数的乘方21.代数式22、列代数式23、代数式的值13.有理数的混和运算14.科学记数法、近似数与有效数字15.用计算器进行简单的数的运算18.单项式27、整式的加减20、整式的见解19、多项式初中数学.数与代数32、一元一次方程39、二元一次方程组45、一元一次不等式和一元一次不等24、归并同类项25、去括号与添括号26、整式的加减法28、等式及其基本性质29、方程和方程的解、解方程30、一元一次方程及其解法31、一元一次方程的应用35、二元一次方程组的解法36、有关见解及性质37、三元一次方程组及其解法举例38、一次方程组的应用43、一元一次不等式40、一元一次不等式及其解法41、不等式的解集44、一元一次不等式组42、不等式和它的基本性质式组46、同底数幂的乘法、单项式的乘法47、幂的乘法、积的乘方51、整式的乘法48、单项式与多项式相乘49、多项式的乘法56、整式的乘除50、平方差与圆满平方根52、多项式乘以单项式55、整式的除法53、单项式除以单项式54、同底数幂的除法63、因式分解61、方法57、提取58、运用公式法59、分组分解法72、分式62、意义60、其他分解法65、分式的乘除法——64、分式的乘除运算69、可化为一元一次方程的分式方程及其应用70、分式的意义和性质71、分式的加减法73、平方根与立方根66、含字母系数的一元一次方程67、分式方程解法、阵根68 分式方程的应用75、数的开方74、实数87、二次根式86、二次根式的意义79、二次根式的乘除法76、最简二次根式77、二次根式的除法78、二次根式的加减法82、二次根式的加减法85、二次根式的混淆运算80、二次根式的加减法81、同类二次根式83、二次根式的混淆运算84、有理化因式数与102、一元二次方程93、一元二次方程的解法98、一元二次方程的意义100、二元二次方程组99、一元二次方程组的根与系数的关系代94、分式方程的解法数97、可化为一元二次方程的分式方程式和无理方程96、分式方程、无理方程的应用101、一元二次方程的应用103、一次函数与一元一次不等式106、一次函数104、一次函数图像的图像和性质108、二次函数——105、正比率函数的图像和性质107 二次函数的有关见解113、函数及其图像109、平面直角坐标系110、函数初111、函数的图像中112、反比率函数数114、线段学116、线段、角115、角117、订交线、对顶角、邻角、补角120、订交线118、垂线、点到直线的距离126、订交、平行123、平行线119、同位角、内错角、同旁内角121、平行线见解及性质122、平行线的判断空124、空间直线、平面的地址关系125、命题、公义、定理间129、与三角形有关的边与图形138、三角形134、全等三角形135、等腰三角形133、直角三角形——132、勾股定理131、与三角形有关的角——130、三角形的内角136、轴对称151、四边形137、基本作图144、平行四边形149、多边形150、中心对称139、平行四边形的见解及其性质140、平行四边形的判断141、矩形的见解、性质和判断142、菱形的见解、性质和判断143、正方形的见解、性质和判断145、梯形的有关见解148、梯形146、等腰梯形的见解、性质和判断147、三角形、梯形的中位线156、比率线段158、相像图形157、相像多边形152、相像三角形的有关见解155、相像三角形153、三角形相像的判断163、解直角三角形154、相像三角形的性质159、解直角三角形161、解直角三角形160、解直角三角形的应162、锐角三角形164、圆的有关见解及对称性空间172、圆的有关性质165、点和圆的地址关系166、过不在同素来线上三点的圆167、三角形的外接圆168、垂径定理及其逆定理初中数与图形169、圆心角、弧、弦、弦心距170、圆周角定理171、圆内接四边形及其性质173.直线和圆的地址关系学185、圆174.切线的判断和性质177.直线和圆的地址关系175.三角形的内切圆176. * 切线长定理179.正多边形和圆——183.弧长和扇形的面积178.正多边形的有关计算180.圆周长、弧长181.圆、扇形、弓形的面积182.圆柱和圆锥的侧面张开图、侧面积184.圆和圆的地址关系186.几何体、几何图形187.平均数188.众数和中位数191.统计初步189.级差、方差、标准差195.统计与概率190.频数、频次、频次散布直方图192.概率初步——概率计算。

第一讲 和绝对值有关的问题一、 知识结构框图：二、 绝对值的意义：(1)几何意义：一般地，数轴上表示数a 的点到原点的距离叫做数a 的绝对值，记作|a|。

(2)代数意义：①正数的绝对值是它的本身；②负数的绝对值是它的相反数；③零的绝对值是零。

也可以写成： ()()()||0a a a a a a ⎧⎪⎪=⎨⎪-⎪⎩当为正数当为0当为负数三、 典型例题例1．（数形结合思想）已知a 、b 、c 在数轴上位置如图：则代数式 | a | + | a+b | + | c-a | - | b-c | 的值等于（ ） A ．-3a B ． 2c －a C ．2a －2b D ． b例2．已知：z x <<0，0>xy ，且x z y >>， 那么y x z y z x --+++的值（ ）A ．是正数B ．是负数C ．是零D ．不能确定符号例3．（分类讨论思想）已知甲数的绝对值是乙数绝对值的3倍，且在数轴上表示这两数的点位于原点的两侧，两点之间的距离为8，求这两个数；若数轴上表示这两数的点位于原点同侧呢？ 例4．（整体思想）方程x x -=-20082008 的解的个数是（ ）A ．1个B ．2个C ．3个D ．无穷多个例5．（非负性）已知|a b －2|与|a －1|互为相互数，试求下式的值．()()()()()()1111112220072007ab a b a b a b ++++++++++说明：（Ⅰ）|a|≥0即|a|是一个非负数；（Ⅱ）|a|概念中蕴含分类讨论思想。

例6．（距离问题）观察下列每对数在数轴上的对应点间的距离 4与2-，3与5，2-与6-，4-与3.并回答下列各题：（1）你能发现所得距离与这两个数的差的绝对值有什么关系吗？答：___ . （2）若数轴上的点A 表示的数为x ，点B 表示的数为―1，则A 与B 两点间的距离可以表示为 ________________.（3）结合数轴求得23x x -++的最小值为 ，取得最小值时x 的取值范围为 ___. （4） 满足341>+++x x 的x 的取值范围为 ______ .第二讲：代数式的化简求值问题一、知识链接1．“代数式”是用运算符号把数字或表示数字的字母连结而成的式子。

初中语文知识结构图字音3.汉字2.字形4.含义5.色彩9.词语 6.近义词辨析7.熟语8.关联词语点号12.标点符号11.误用辨析47 27.基础知识13.常见修辞格初15.修辞中辞格辨语词类文20.语法17.短语18.复句19.辨析修改病句21.作家作品24.文学文化常识22.名篇名句23.文化常识45.知识体系26.语言表达——25.简明、连贯、得体28.常见实词31.文章内容的归纳，中心的概括29.常见虚词34.古代诗文阅读30.一词多义32.实词、虚词33.文章内容的理解（翻译、断句）35.文体知识36.依据作品内容进行的合理推断37.作文作品语言、表达技巧和形象的鉴赏38.文学作品思想内容、作者态度的评价44.现代文阅读39.重要句子的理解和解释40.重点词语的理解41.文中信息的分析和筛选42.内容的归纳，中心的概括43.结构的分析，思路的把握46.中考复习初中数学知识结构图1.有理数（正数与负数）2.数轴6.有理数的概念 3.相反数4.绝对值5.有理数从大到小比较7.有理数的加法、加法运算律17.有理数8.有理数的减法9.有理数的加减混和运算10.有理数的乘法、乘法运算16.有理数的运算11.有理数的除法、倒数12.有理数的乘方21.代数式13.有理数的混和运算22、列代数式14.科学记数法、近似数与有效数字23、代数式的值15.用计算器进行简单的数的运算18.单项式27、整式的加减20、整式的概念19、多项式24、合并同类项25、去括号与添括号26、整式的加减法28、等式及其基本性质29、方程和方程的解、解方程32、一元一次方程30、一元一次方程及其解法198 31、一元一次方程的应用初、二元一次方程组的解法中36、相关概念及性质数193 39、二元一次方程组37、三元一次方程组及其解法举例学数、一次方程组的应用. 与43、一元一次不等式40、一元一次不等式及其解法代45、一元一次不等式41、不等式的解集数和一元一次不等、一元一次不等式组42、不等式和它的基本性质式组46、同底数幂的乘法、单项式的乘法47、幂的乘法、积的乘方51、整式的乘法48、单项式与多项式相乘49、多项式的乘法56、整式的乘除50、平方差与完全平方根52、多项式乘以单项式55、整式的除法53、单项式除以单项式54、同底数幂的除法57、提取61、方法58、运用公式法63、因式分解59、分组分解法62、意义60、其他分解法66、含字母系数的65、分式的乘除法——64、分式的乘除运算一元一次方程69、可化为一元一次方程的分式方程及其应用67、分式方程解法、72、分式70、分式的意义和性质阵根71、分式的加减法68分式方程的应用73、平方根与立方根75、数的开方74、实数86、二次根式的意义76、最简二次根式79、二次根式的乘除法77、二次根式的除法87、二次根式78、二次根式的加减法82、二次根式的加减法80、二次根式的加减法81、同类二次根式85、二次根式的混合运算83、二次根式的混合运算84、有理化因式93、一元二次方程的解法193 98、一元二次方程的意义数100、二元二次方程组与102、一元二次方程99、*一元二次方程组的根与系数的关系代94、分式方程的解法数97、可化为一元二次方程95、*无理方程的意义、解法的分式方程式和无理方程96、分式方程、无理方程的应用101、一元二次方程的应用103、一次函数与一元一次不等式106、一次函数104、一次函数图像的图像和性质105、正比例函数的图像和性质108、二次函数——107二次函数的有关概念113、函数及其图像109、平面直角坐标系198 110、函数初111、函数的图像中112、反比例函数数114、线段学116、线段、角115、角117、相交线、对顶角、邻角、补角120、相交线118、垂线、点到直线的距离119、同位角、内错角、同旁内角126、相交、平行123、平行线121、平行线概念及性质122、平行线的判定194 124、空间直线、平面的位置关系空125、命题、公理、定理间129、与三角形有关的边与134、全等三角形图135、等腰三角形形138、三角形133、直角三角形——132、勾股定理131、与三角形有关的角——130、三角形的内角136、轴对称139、平行四边形的概念及其性质137、基本作图140、平行四边形的判定144、平行四边形141、矩形的概念、性质和判定149、多边形142、菱形的概念、性质和判定151、四边形150、中心对称143、正方形的概念、性质和判定145、梯形的相关概念148、梯形146、等腰梯形的概念、性质和判定147、三角形、梯形的中位线、比例线段158、相似图形157、相似多边形、相似三角形的相关概念155、相似三角形153、三角形相似的判定、相似三角形的性质159、解直角三角形161、解直角三角形160、解直角三角形的应163、解直角三角形162、锐角三角形164、圆的有关概念及对称性165、点和圆的位置关系194. 166、过不在同一直线上三点的圆空172、圆的有关性质167、三角形的外接圆间168、垂径定理及其逆定理198. 与169、圆心角、弧、弦、弦心距初图170、圆周角定理中形171、圆内接四边形及其性质数173.直线和圆的位置关系学185、圆174.切线的判定和性质177.直线和圆的位置关系175.三角形的内切圆176. *切线长定理179.正多边形和圆——178.正多边形的有关计算圆周长、弧长183.弧长和扇形的面积181.圆、扇形、弓形的面积圆柱和圆锥的侧面展开图、侧面积184.圆和圆的位置关系186.几何体、几何图形187.平均数188.众数和中位数191.统计初步189.级差、方差、标准差195.统计与概率190.频数、频率、频率分布直方图192.概率初步——概率计算196.中考复习197.总复习初中英语知识结构图1.名词的数3. 名词 2.名词的格4.人称代词5.物主代词6.反身代词10.代词7.指示代词8.不定代词9.疑问代词11.位置14.形容词12.形容词的用法13.比较级和最高级15.副词的用法17.副词16.比较级和最高级18.不定冠词41.词类21.冠词19.定冠词22.一般现在时20.零冠词23.一般过去时24.一般将来时29.动词的时态25.现在进行时26.过去进行时27.现在完成时73. 28.过去完成时初31.动词的语态——30.被动语态中 32.不定式英 41.动词 35.非谓语动词 33.分词语 34.动名词56.语法结构36.连系动词37.助动词42.数词38.情态动词43.介词39.短语动词44连词40.行为动词的及物性和不及物性45.疑问句——反意疑问句49.句子的种类46.祈使句47.感叹句50.句子的成分48.There be结构51.主谓一致52.名词性从句——宾语从句59.句子55复合句53.定语从句56.简单句54.状语从句57.it的用法60.问候58.倒装结构61.感谢和应答62.祝愿、祝贺和应答63.道歉、遗憾和应答70.交际64.提供（帮助等）和应答65.请求、允许和应答66.劝告和建议71.语音67.问路和应答72.拼写68.问时间、日期和应答初中物理知识结构图1.度的测量4.测量的初步知识 2.误差3.间的测量7.简单的运动 5.机械运动6.匀速直线运动8.声音的发生、传播12.声现象9.声音的特性10.噪音的危害和控制11.超声和次声13.温度温度计17.物态变14.溶化和凝固15.汽化和液化16.升华和凝华18.光源光的直线传播19.光的反射反射定律24.光现象20.光的色散颜色21.平面镜、平面镜成像22.光的折射现象23.看不见的光25.透镜29透镜及其应用26.凸透镜成像规律27.眼睛和眼镜28.显微镜和望远30.天平与质量31.密度35.质量和密度32.物质的概述33.测量物质的密度34.密度的应用重力37.同一条直线上二力的合成41.力38.摩擦力39.弹力力的概述及力的测量牛顿第一定律44.力和运动43.二力平衡45.浮力的产生48.浮力46.浮力的大小阿基米德原理47.浮力的应用杠杆51.简单机械50.滑轮（其他简单机械）52.功55.功、功率与机械效率53.机械效率54.功率56.势能59.机械能57.机械能及其转化58.功能60.分子热运动64.分子动理论、内能61.内能62.能量守恒定律63.热量的计算比热容67.电路65.电学的基本概念电路的连接串联和并联70.电流68.电流电流表69.串并联电路中电流的规律73.电压71.电压电压表72.串并联电路中电压的规律76.电阻74.变阻器75.串并联电路中电阻的规律77.电功80.电功电功率电热78.电功率79.电和热电生磁82.电磁继电器86.电和磁83.磁现象84.磁场对电流的作用磁生电87.电话91.信息的传递88.电磁波89.电磁波的发射和接收90.信息之路92.能源家族（核能太阳能）95.能源与可持续发展93.能源革命能源与可持续发展94.能源的开发和利用96.液体的压强97.压强和压力98.大气压强99.内能利用、热机100.欧姆定律101.家庭电路和安全用电102.液体压强和流速的关系初中化学知识结构图1.元素——元素的概念和分类2.离子——核外电子排布的初步知识3.相对分子量6.有关化学式的计算 4.计算化合物中某种元素的质量分数5.计算化合物中个元素的质量比物质构成的奥秘9.化合价常见元素化合价8.化合价与化学互推10.原子11.分子的概念和性质12.物质的分类13.化学式的书写、读法、意义15.溶液、溶质、溶剂19.溶液16.饱和溶液和不饱和溶液17.溶解度18.溶液中溶质的质量分数、溶剂的配制22.氧气20.氧气的性质和用途21.氧气制取25.水23.水的组成、硬水和软水24.保护水资源、节约用水58. 28.二氧化碳二氧化碳的制取初二氧化碳的性质、用途中——溶液酸碱度的表化30.几种常见的酸学47.身边的化学物质35.二氧化碳31.中和反应及其应用32.几种常见的碱33.几种常见的盐化学肥料（特性、种类）38.空气36.空气的主要成分37.防治空气污染39.金属活动性顺序43.金属40.生铁和钢41.常见金属、金属材料、合金42.金属的物理性质、化学性质44.氢气45.碳46.一氧化碳50.物质的变化48.物理变化、化学变化49.物理性质、化学性质51.反应类型——氧化反应、还原反应52.催化剂与催化作用57.物质的化学变化53.质量守恒定律54.化学方程提供的信息、书写及其配平55.利用化学方程式的计算56.综合计算题。