【精品】课件---高斯定理应用

为高斯面，电通量为
E dS

E4π r 2
q内
0
• 球外( r > R )
q内

4π 3
R3
E

3 0
R3 r2
• 球内 ( r < R )
q内

4π 3
r3
E r 3 0
若 ＝ (r) ? 如 (r)＝A /r
r+
++r+
+ +
R+++
E dl a E dl b E dl c E dl d E dl
b
d
a
b
a E1dl c E2dl

d
cE
0
不是静电场
(2) 环路定理要求电力线不能闭合。
(3) 静电场是有源、无旋场，可引进电势能。
三. 电势能
• 电势能的差 力学
第二讲 应用高斯定理求场强分布
静电场高斯定理
e
E dS
1
S
0
q内
e
E dS
1
S
0
dV
V
真空中的任何静电场中，穿过任一闭合曲面的电通量，等
于该曲面所包围的电荷电量的代数和乘以 1 0
(1) 意义 反映静电场的性质 —— 有源场
(2) 通量的一般意义: (3) 注意

3 0
r1
E2

4 3
r23 ( 4 0r22
)
r2
0

3 0
r2
o o
E E1 E2

磁场计算
在计算磁场分布时，高斯定理也发挥了重要 作用。它可以用来确定磁场线穿过任意封闭 曲面的通量，进而推导出磁场分布。
在工程学科中的应用
电力工程
在电力工程中，高斯定理被广泛应用于电磁 场分析和计算。例如，在输电线路和变压器 设计中，需要利用高斯定理来评估电磁场对 周围环境的影响。
电子工程
在电子工程领域，高斯定理用于分析集成电 路和电子元件中的电磁场。通过高斯定理， 工程师可以更好地理解电子元件的工作原理
要点二
量子计算
随着新型材料科学的发展，高斯定理在研究材料电磁性质 、导电性能等方面将发挥更大的作用。
量子计算领域的发展为高斯定理提供了新的应用场景，有 助于更深入地理解量子力学中的相关概念。
高斯定理在数学领域的发展趋势
数学物理
随着数学物理的不断发展，高斯定理在数学物理中的地 位将更加重要，有助于推动数学物理理论的发展。
总结词
均匀带电圆环产生的电场分布可以通过高斯定理求解。
详细描述
首先，我们需要将均匀带电圆环分割成许多小的带电圆环，然后利用高斯定理计算每个小圆环产生的 电场强度。最后，将所有小圆环的电场强度进行叠加，得到均匀带电圆环的总电场分布。
例题三：求无限长均匀带电直线的电场分布
总结词
无限长均匀带电直线产生的电场分布也 可以通过高斯定理求解。
《高斯定理例》ppt课件
目录
• 高斯定理简介 • 高斯定理的数学推导 • 高斯定理的例题解析 • 高斯定理的实践应用 • 高斯定理的未来发展
01
高斯定理简介
高斯定理的定义
总结词
高斯定理是描述闭合曲面电场分 布的定理。
详细描述
高斯定理表述为通过任意闭合曲 面的电场通量等于该闭合曲面所 包围的电量的代数和除以真空中 的介电常数。

6 – 2 高斯定理
第六章 静电场
一 电场线 （电场的图示法） 2023最新整理收集 do something
规定 1） 曲线上每一点切线方向为该点电场方向,
2） 通过垂直于电场方向 单位面积电场线数为 该点电场强度的大小. E E dN / dS
S
E
1
6 – 2 高斯定理
第六章 静电场
点电荷的电场线
第六章 静电场
由多个点电荷产生的电场
E E1 E2
q1
q2
Φe
E dS
S
S
Ei dS
qi
i
i(内） S
Ei
dS
i（外） S
Ei
dS
i（外） S
Ei
dS
0
1
Φe
i（内） S
Ei
dS
0
qi
i (内）
17
6 – 2 高斯定理
第六章 静电场
高斯定理 Φe
h
+
+o
y
x+
23
6 – 2 高斯定理
第六章 静电场
例4 无限大均匀带电平面的电场强度
无限大均匀带电平面，单位面积上的电荷，即电
r 荷面密度为 ，求距平面为 处的电场强度.
解 对称性分析：E垂直平面
选取闭合的柱形高斯面
E
dS
S＇
S
0 底面积
S＇
2S＇E S＇
0
E 20 24
6 – 2 高斯定理
6
6 – 2 高斯定理
第六章 静电场
电场线特性
1） 始于正电荷,止于负电荷(或来自无穷远,去 向无穷远).
2） 电场线不相交. 3） 静电场电场线不闭合.

分布具有一定对称性的电场问题。
.
11
例2 一无限长均匀带电细棒，其线电荷密度为 求距细棒为a处的电场强度。
解 以细棒为轴作一个高为l、截面半径 为a的圆柱面，如下图。以该圆柱面为高 斯面，运用高斯定理。由于对称性，圆 柱侧面上各点的场强 的E 大小相等， 方l a 向都垂直于圆柱侧面向外。
通过高斯面S的电通量可分为圆柱侧
EdS
1
S
qi
0 i n s i,id e
1. 证明包围点电荷q 的同心球面S 的电通量
球面上各点的场强方向与其径向相同。
球面上各点的场强大小由库仑定律给出。
deE dS EdS4π 10rq2dS
r
q
E S
.
7
deE dS EdS4π 10rq2dS
e Sd e S4 π q 0 r2d S 4 π q 0 r2S d S q 0
的数学成就遍及各个领域，在数学许多方面的贡献都有着划时
代的意义．并在天文学，大地测量学和磁学的研究中都有杰出
的贡献．1801年发表的<算术研究>是数学史上为数不多的经
典著作之一，它开辟了数论研究的全新时代．非欧几里得几何
是高斯的又一重大发现，他的遗稿表明，他是非欧几何的创立
者之一．高斯致力于天文学研究前后约20年，在这领域内的伟
x
度通量为
z
e 1 2 3 4 5
1E1ScoπsE1S;2340
5EcoSs5E1S即通过闭合曲面的电
eE1SE1S0 场强度通量为零。
.
6
三、 高斯定理〔Gauss theorem）
静电场中任意闭合曲面S的电通量，等于该曲面
所包围的电量除以ε0，而与S以外的电荷无关。

解：电场分布具有轴对称性 过P点作一个以带电直线为轴，

dS
r
E
以l 为高的圆柱形闭合曲面S
为高斯面
作
E
P
l
e SEdS dS
侧 E d S 上 E d 底 S 下 E d 底 SE
侧 E d S E 侧 d S E 2 rl
根据高斯定理得
E2rl 1l 0
E 20r O 电场分布曲线
r
13
总结
用高斯定理求电场强度的步骤： (1) 分析电荷对称性； (2) 根据对称性取高斯面；
高斯面必须是闭合曲面 高斯面必须通过所求的点 高斯面的选取使通过该面的电通量易于计算
(3) 根据高斯定理求电场强度。
14
高斯定理应用//课堂练习
求 均匀n 电场E中一半n球面[补的偿电法通]量。
n
场强方向沿电力线切线方向， 一半径为R的无限长均匀带电圆柱体，体电荷密度
均匀带电球体的电场强度分布
场强大小决定电力线的疏密。 （连续分布的源电荷）
均匀带电球面，总电量为Q，半径为R
求均匀电场中一半球面的电通量。
以点电荷为例建立 e——q 关系:
dN 一均匀带电球体，半径为R，电荷密度为ρ，现在球内挖去一半径为r(r <R)的球体。 E 结论: e 与曲面的形状及 q 在曲面内的位置无关。
高斯面必须通过所求的点
已知无限大板电荷体密度为 ，厚度为d
（不连续分布的源电荷）
2
E dS EdS E dS E4r 则 在空腔处补上球体（ ρ 、r）后，
P
E
+ dS
+ R r+
++
Q+

讨论：
1、电荷分布无对称性，只用高斯定理能求场强
分布吗？
(x0,y0,z0)
E (x,y,z)?
EdS
S
1 qi 0 (S)
不能。但这不在于数学上的困难。
高斯定理只是静电场两个基本定理之一，与下
面讲的环路定理结合，才能完备描述静电场。
16
2、对所有平方反比的有心力场，高斯定理
都适用。
引通力过场闭场合强曲:面通g 量-:Grm2g rˆdS -4Gm i
场强 E 能否提出积分号 带电体电荷分布的对称性 利用高斯定理求静电场的分布
+
电荷分布球对称 电场分布球对称（场强沿径向，只与半径有关）
场强 E 能否提出积分号
高斯面的选取使通过该面的电通量易于计算 电力线连续：不会在没有电荷的地方中断
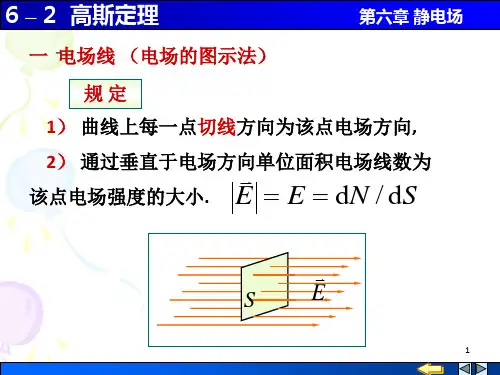
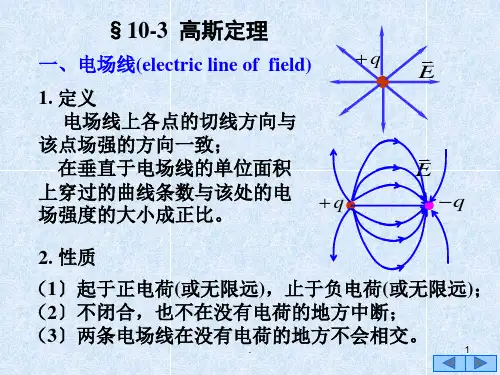
二、 均匀带电球体的电场分布
+
（2）选半径r高h的同轴圆柱面为高斯面
3 0
(r1
- r2 )
3 0
0R
r
【思考】为什么在r = R 处E 不连续？
2
二、 均匀带电球体的电场分布
球体内：
E
1
Qrrˆ r
40R3 30
球体外：
E
E
Q
rˆ
40r2
0R
r
3
三、无限长圆柱面(线电荷密度)的电场分布
解.（1）场强轴对称沿径向
（2）选半径r高h的 同轴圆柱面为高斯面 h
S
r
E
（3）柱面外
S'
E 2 r h E d S E d S h /0
总结：
S
i
场的观点 场强叠加原理
点电荷场叠加（任意电荷分布）电场分布

2 0r
场强方向沿半径方向
17
无限长均匀带电圆柱面的场强分布图线
E
E
0
rR rR
20r
E
2r 0
E0
oR
r
2021/4/24
18
练习：求均匀带电圆柱体的场强分布，已知R，
通量
e E • ds E • ds E • ds E • ds
s
上底
下底
侧面
0 0 E2rl
rR
闭合曲面所包围的电荷电量的代数和除以 0 ,
而与闭合面外的电荷无关。其数学表达式为
e
E dS
S
几点说明 :
qi
0
1、高斯定理对于任意电场都成立
2、通过闭合曲面S 的电通量，只与闭合面内的电荷有关, 而 与闭合面外的电荷无关；
3、S 面上的场强是 S 面内外的电荷共同激发的。
4、高斯定理说明：静电场为有源场, 正电荷是静电场的源 头 ；负电荷为静电场的尾闾 。
5-4 电场强度通量 高斯定理
一、电场强度通量(电通量)
1、电场线(电力线)
Ea
a•
ds b •••
Eb
规定：1、曲线的切线方向与该点的场强方向一致；
2、穿过垂直于电场方向单位面积上曲线的条数 （电场线的面密度） ，等于该点的电场强度的大小。
E de ds
电场线越密处，场强越大，反之，场强越小。
即在同轴圆柱面上各点场强大小相等，场 强方向沿半径方向。
16
解：电场具有轴对称性，如图取同轴闭合圆柱面作为高斯面
e E • ds E • ds E • ds E • ds
s
上底
下底
侧面
R

R2
R2
c.
R1
<r
<R2
： R2 r
4q10r2er•erdr2
d. r =R1 ：
4q10(1 rR 12)40q (1 R 2 q2R 2)
E q1 4 0 r 2
q1 q2
14 q10(R 1 1R 1 2)4 0q (1 R 2 q2 R 2)
4 0 r 2 r
q 1 (11 1 ) q 2
D是电位移矢量，是一个辅助物理量，其本身并没有 明确的物理意义，然而引入它可以方便地表达出任一 点的场量与场源之间的关系，即电位移矢量的散度等 于该点分布的自由电荷体密度。
E和D的分布都与介质有关。但是穿过闭合曲面的D通 量仅与该闭合面所包围的自由电荷有关，而与介质中 的束缚电荷无关。
22
点电荷的电场中置入任意一块介质
0 R1 R2 R2+R2
40 R 1 R 2 R 2R 2 40 (R 2R 2)
31
例2 同轴电缆有两层绝缘体，分界面也是同轴圆柱面，
尺寸如图。内外导体之间的电压为U，求场中各处电场。
解: ① 分析电荷和场分布情况 ：
② 求场强分布情况： （方向、对称性）
作半径为r、长为l的同轴圆柱面（包括两个底面）
16
2、介质中的高斯定律
表面S为电介质中一假想闭合面，不包含介质的表面； 自由电荷q1 、 q2 、 q3分布在导体表面S1 、 S2 、 S3上：
1
E•dS
S
0
(q
qP
)
S
q d V dS P V V 1 V 2 V 3 P
0 S S 1 S 2 S 3 P
q1 S1
S3

a.无限大均匀带电薄板
b.无限大厚平板，电荷沿与板中心面平行的同一平 面均匀分布，沿与平面垂直的方面均匀与否都可。
电场也具有上述对称性，即1）在与带电体平行， 并关于带电体中心面镜面对称的任意一对无限大平 面上的电场强度大小都相等。2）各点电场强度的 方向处处与该点平面垂直，并关于带电体中心面镜 面对称。
垂直平面指向考察点（若， 0 则由考察点指
向平面）。
静电场的高斯定理
-
1
静电场的高斯定理
高斯定理的表述
在真空中通过任意闭合曲面的电通量等于该曲
面所包围的一切电荷的代数和除以 0。这就是真空
中的高斯定理。高斯定理中闭合曲面称为高斯面。
数学表达式为：
e
s
EdS1
0
qi
S内Biblioteka 思考如果没有库仑 定律高斯定理 是否成立？
体分布的带电体
1
e s E dS 0
S，两底面到带电平面距离相同。
通过圆柱形高斯面的E通量
e
E dS
E dS E dS E dS S
S1 S2 S3 E e ES ES
S1
E
圆柱形高斯面内电荷
q S
S2
σ
- S1 S2 S
S3
18
由高斯定理得 E
2ES S / 0
S
E
E
2 0
er
均匀电场
σ
3．计算电通量和高斯面内所包围的电荷的代数和， 最后由高斯定理求出场强。
-
10
例7-8求电荷呈球对称分布时所激发的电场分布
思考分析解题的步骤 电荷呈球对称分布时有两种情况
l均匀带电球体的电场。
球半径为R，体电荷密度为。