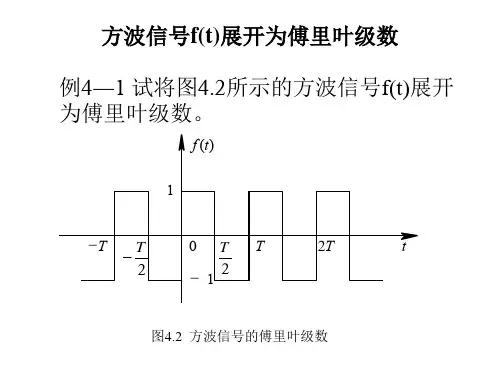
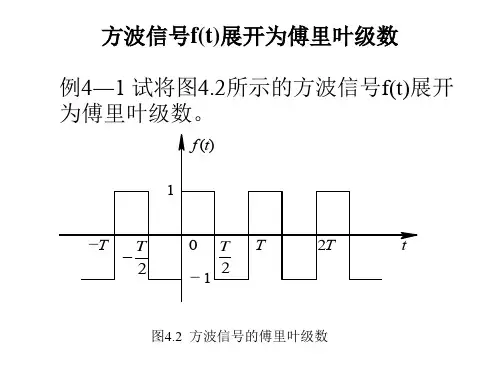
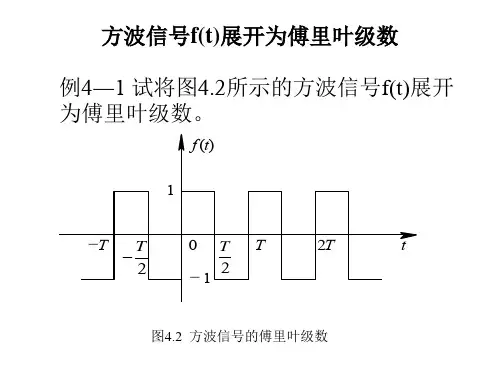
方波信号展开为傅里叶级数

几种常见函数的傅里叶变换及推导傅里叶变换是数学中一种非常重要的变换方法，它可以将一个函数在时域（或空域）中的表达转换为频域中的表达。

在信号处理、图像处理、通信等领域中被广泛应用。

本文将介绍几种常见函数的傅里叶变换及推导过程。

1. 方波函数的傅里叶变换方波函数是一种周期函数，它在每个周期内以不同的幅度交替出现。

方波函数的傅里叶变换可以通过将方波函数表示为一系列正弦函数的和来推导得到。

假设方波函数为f(t)，其周期为T，傅里叶变换为F(ω)。

根据傅里叶级数展开的性质，方波函数可以表示为：f(t) = (1/2) + (2/π)sin(ωt) + (2/π)sin(2ωt) + (2/π)sin(3ωt) + ...其中，ω = 2π/T是方波函数的角频率。

根据傅里叶变换的定义，可以得到方波函数的傅里叶变换为：F(ω) = (1/2)δ(ω) + (1/2π)[δ(ω-ω0) - δ(ω+ω0)] + (1/2π)[δ(ω-2ω0) - δ(ω+2ω0)] + (1/2π)[δ(ω-3ω0) - δ(ω+3ω0)] + ...其中，δ(ω)是狄拉克函数，表示单位冲激函数。

傅里叶变换的结果是一系列的冲激函数，每个冲激函数对应一个正弦函数的频谱分量。

2. 高斯函数的傅里叶变换高斯函数是一种常用的连续函数，其在数学和物理学中有广泛的应用。

高斯函数的傅里叶变换可以通过将高斯函数表示为指数函数的平方和来推导得到。

假设高斯函数为f(t)，傅里叶变换为F(ω)。

根据高斯函数的定义，可以得到：f(t) = e^(-αt^2)其中，α是常数。

根据傅里叶变换的定义，可以得到高斯函数的傅里叶变换为：F(ω) = √(π/α)e^(-ω^2/(4α))高斯函数的傅里叶变换仍然是一个高斯函数，只是幅度和频率发生了变化。

3. 矩形函数的傅里叶变换矩形函数是一种常见的函数，它在一个有限区间内的值为常数，而在其他区间内的值为零。

矩形函数的傅里叶变换可以通过将矩形函数表示为两个单位阶跃函数的差来推导得到。

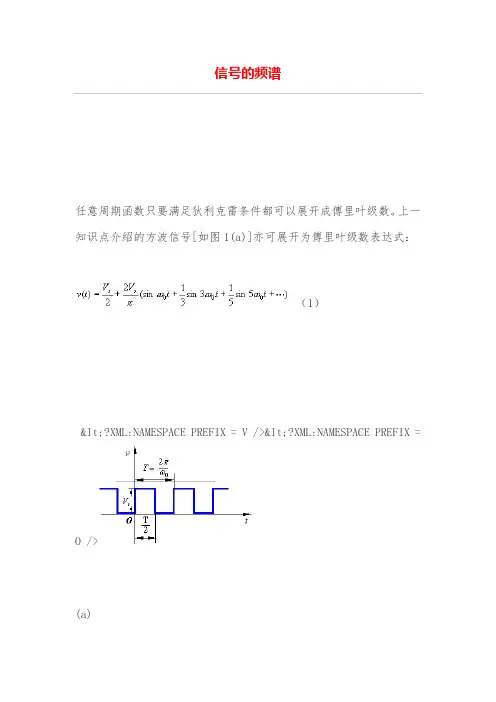
信号的频谱任意周期函数只要满足狄利克雷条件都可以展开成傅里叶级数。

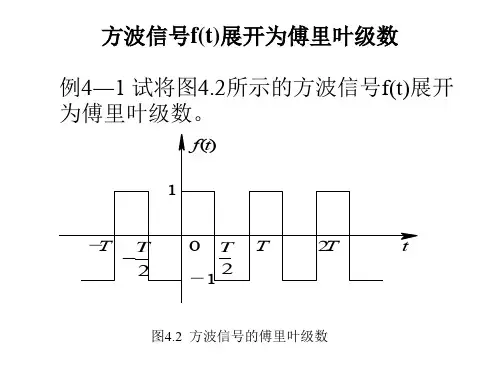
上一知识点介绍的方波信号[如图1(a)]亦可展开为傅里叶级数表达式：（1）<?XML:NAMESPACE PREFIX = V /><?XML:NAMESPACE PREFIX = O />(a)(b) 图1(a)(b)图2式中，，是方波信号的直流分量，称为该方波信号的基波，它的周期与方波本身的周期相同。

式（1）中其余各项都是高次谐波分量，它们的角频率是基波角频率的整数倍。

由于正弦函数的单纯性，在作信号分析时，可以只考虑其幅值电压与角频率的函数关系，于是式（1）的正弦级数可以表达为图1(b)所示的图解形式，其中包括直流项（ω=0）和每一正弦分量在相应角频率处的幅值。

像这样把一个信号分解为正弦信号的集合，得到其正弦信号幅值随角频率变化的分布，称为该信号的频谱。

图1(b)称为方波信号的频谱图，是方波在频域的表达方式。

从傅里叶级数特性可知，许多周期信号的频谱都由直流分量、基波分量以及无穷多项高次谐波分量所组成，频谱表现为一系列离散频率上的幅值。

上述正弦信号和方波信号都是周期信号。

客观物理世界的信号远没有这样简单，如果从时间函数来看，往往很难直接用一个简单的表达式来描述，如图2(a)所示炉温变化曲线就是一非周期性时间函数波形。

对于非周期信号，运用傅里叶变换可将其表达为一连续频率函数形式的频谱，它包含了所有可能的频率（0≤ω<∞）成分。

图2(b)示意出图2(a)的频谱函数。

实际物理世界的各种非周期信号，随角频率上升到一定程度，其频谱函数总趋势是衰减的。

当选择适当的ωc （截止角频率）点把频率高端截断时，并不过多地影响信号的特性。

通常把保留的部分称为信号的带宽。

由上分析可知，信号的频域表达方式可以得到某些比时域表达方式更有意义的参数。

信号的频谱特性是电子系统有关频率特性的主要设计依据。

确定一个任意非周期信号的频谱在计算机普及应用之前并非易事。

方波信号的傅里叶级数展开方波信号是一种特殊的周期信号，在每个周期内信号值交替地取正弦波的最大值和最小值。

它可以用傅里叶级数展开来表示，下面我将详细介绍关于方波信号的傅里叶级数展开的相关内容。

傅里叶级数是一种将一个周期性函数分解为一系列正弦和余弦函数的无穷级数的表示方法。

对于一个周期为T的函数f(t)，其傅里叶级数表示为：f(t) = a0/2 + Σ(an*cos(nωt) + bn*sin(nωt))其中，a0/2表示直流分量，an和bn分别表示正弦和余弦分量的系数，ω为角频率，等于2π/T。

对于方波信号，其周期为T，即一个周期内正弦波的最大值和最小值的持续时间。

方波信号可以表示为一个由无限多个正弦波组成的傅里叶级数。

在方波信号的傅里叶级数展开中，直流分量a0/2表示方波的平均值，等于正弦波最大值和最小值的平均值。

对于幅值为A，周期为T的方波信号，其直流分量a0/2等于A/2。

正弦和余弦分量的系数an和bn可以通过积分计算得到。

由于方波信号在一个周期内的正弦和余弦分量只有在0到T/2的时间段内有贡献，所以对an和bn的计算可以将积分区间限制在0到T/2。

根据傅里叶级数的定义，an和bn的计算公式为：an = (2/T) * ∫[0,T/2] (f(t)*cos(nωt) dt)bn = (2/T) * ∫[0,T/2] (f(t)*sin(nωt) dt)其中，f(t)为方波信号。

对于方波信号，可以将其正弦和余弦分量表示为：an = (2/T) * ∫[0,T/2] (A*cos(nωt) dt)= (2/T) * (A/nω) * [sin(nωt)] from 0 to T/2= (2/T) * (A/nω) * sin(nωT/2)bn = (2/T) * ∫[0,T/2] (A*sin(nωt) dt)= (2/T) * (-A/nω) * [cos(nωt)] from 0 to T/2= (2/T) * (-A/nω) * [cos(nωT/2) - 1]根据傅里叶级数展开的定义，方波信号可以表示为：f(t) = A/2 + Σ[(2A/(nπ)) * sin(nωt)] from n = 1 to ∞其中，A为方波信号的幅值，T为方波信号的周期。

占空比为d的方波傅里叶级数方波是一种特殊的周期波形，由一组连续的正半区和负半区组成。

占空比为d的方波是指正半区的持续时间占整个周期时间的比例为d。

傅里叶级数是一种将周期函数分解成余弦或正弦函数的无穷级数的方法。

占空比为d的方波可以表示为一个基频为f的正弦波的和，其中每个正弦波的幅值和相位由方波的占空比决定。

我们可以使用傅里叶级数展开占空比为d的方波，得到其频谱特性。

占空比为d的方波的傅里叶级数展开可以表示为以下形式的级数：f(t) = A/2 + Σ(A/(2nπf) * sin(2nπft)) for odd values of n其中，f(t)是占空比为d的方波的函数形式，A是方波的幅值，f是方波的频率，n为奇数，Σ表示级数求和。

上述公式中，A/2表示方波的直流分量，Σ(A/(2nπf) * sin(2nπft))表示方波的交流部分。

在这个级数中，每个正弦波的频率是基频f的n倍，幅值与频率成反比。

由于只考虑奇数倍频的正弦波，这个级数仅包含奇次谐波。

通过调整幅值和相位的系数，可以得到相应占空比为d的方波的傅里叶级数展开。

占空比为d的方波的傅里叶级数展开可用于分析方波信号在频域上的特性。

通过对级数中各项的幅值和相位进行调整，可以改变方波的波形以及频谱特性。

这在通信、电子音乐以及其他需要特定波形的应用中具有重要意义。

总之，占空比为d的方波可通过傅里叶级数展开来表示。

傅里叶级数提供了一种将方波分解成一系列余弦或正弦波的方法，从而帮助我们理解方波的频率特性。

对方波的傅里叶级数展开的研究对于各种应用领域都具有重要意义。

maple 傅里叶级数Maple是一款强大的数学软件，可以用来进行各种数学计算和分析。

其中，傅里叶级数是Maple中的一个重要功能，可以用来分析周期性信号的频谱特征。

傅里叶级数是一种将周期性信号分解为一系列正弦和余弦函数的方法。

它的基本思想是将一个周期为T的函数f(t)表示为一系列正弦和余弦函数的线性组合，即：f(t) = a0 + Σ(an*cos(nωt) + bn*sin(nωt))其中，a0、an、bn是待求系数，ω=2π/T是角频率，n是正整数。

这个式子被称为傅里叶级数公式。

在Maple中，可以使用FourierSeries函数来计算傅里叶级数。

例如，对于一个周期为2π的方波信号，可以使用以下代码来计算其傅里叶级数：f := piecewise(-Pi < x and x < 0, -1, 0 < x and x < Pi, 1, 0); FourierSeries(f, x = -Pi .. Pi);其中，piecewise函数用来定义方波信号的取值范围，FourierSeries 函数用来计算傅里叶级数。

运行以上代码，可以得到以下结果：1/2*Pi - 4/Pi*sin(x) + 4/(3*Pi)*sin(3*x) - 4/(5*Pi)*sin(5*x) +4/(7*Pi)*sin(7*x) - 4/(9*Pi)*sin(9*x) + 4/(11*Pi)*sin(11*x) -4/(13*Pi)*sin(13*x) + 4/(15*Pi)*sin(15*x) - 4/(17*Pi)*sin(17*x) + 4/(19*Pi)*sin(19*x) - 4/(21*Pi)*sin(21*x) + 4/(23*Pi)*sin(23*x) - 4/(25*Pi)*sin(25*x) + 4/(27*Pi)*sin(27*x) - 4/(29*Pi)*sin(29*x) + 4/(31*Pi)*sin(31*x) - 4/(33*Pi)*sin(33*x) + 4/(35*Pi)*sin(35*x) - 4/(37*Pi)*sin(37*x) + 4/(39*Pi)*sin(39*x) - 4/(41*Pi)*sin(41*x) + 4/(43*Pi)*sin(43*x) - 4/(45*Pi)*sin(45*x) + 4/(47*Pi)*sin(47*x) - 4/(49*Pi)*sin(49*x) + 4/(51*Pi)*sin(51*x) - 4/(53*Pi)*sin(53*x) + 4/(55*Pi)*sin(55*x) - 4/(57*Pi)*sin(57*x) + 4/(59*Pi)*sin(59*x) - 4/(61*Pi)*sin(61*x) + 4/(63*Pi)*sin(63*x)这个结果表示了方波信号的傅里叶级数，其中包含了无穷多个正弦函数的系数。

傅里叶计算方波频率傅里叶分析是一种将一个信号进行频谱分解的数学方法。

它通过将信号分解为一系列正弦和余弦函数的和来描述其频谱内容。

方波信号是一种周期性信号，由一系列矩形脉冲组成，因此可以通过傅里叶分析来计算其频率。

要计算方波信号的频率，首先需要了解方波信号的数学定义。

方波信号可以定义为一个周期函数，其周期为T，占空比为d（d为0到1之间的值），即方波的脉冲宽度为dT。

方波信号可以用以下公式表示：f(t) = A * sign(sin(2πt/T))其中，sign是符号函数，其取值为1或-1，取决于sin(2πt/T)的正负号。

A是方波信号的幅值，t是时间。

接下来，我们需要将方波信号展开为一系列正弦和余弦函数的和，以便进行傅里叶变换。

根据傅里叶级数的定义，我们知道方波信号可以展开为如下形式的级数：f(t) = (4A/π) * [sin(2πt/T) + (1/3) * sin(6πt/T) + (1/5) * sin(10πt/T) + ...]这个级数包含了基频sin(2πt/T)，以及一系列的谐波，其频率是基频的整数倍。

因此，我们可以通过计算这些谐波频率的整数倍来得到方波信号的频率。

首先，我们计算基频的频率。

基频对应于sin(2πt/T)的频率，即2π/T。

我们可以通过基频的周期来计算频率，即f = 1/周期。

对于方波信号，其周期为T，所以基频的频率为f0 = 1/T。

接下来，我们计算谐波的频率。

谐波对应于sin(nωt)，其中n为整数，ω为基频的角频率，即2πf0。

我们可以通过将基频频率乘以谐波的整数倍来得到谐波的频率，即fn = n*f0。

例如，如果方波信号的周期为T=1秒，即频率为f0=1/T=1Hz。

那么基频的频率为f0=1Hz。

而第一个谐波的频率为f1=2f0=2Hz，第二个谐波的频率为f2=3f0=3Hz，以此类推。

通过计算基频和谐波的频率，我们可以得到方波信号的频率。

方波信号的频率是基频和所有谐波频率的集合。

方波信号表达式
方波信号表达式是用数学符号描述方波信号的方程式。

方波信号是一种特殊的周期性信号，其波形为由高电平和低电平交替组成的矩形波形。

方波信号表达式由一系列的数学函数组成，用以表示方波信号的特征和行为。

一种常用的方波信号表达式是使用以时间为自变量的函数来描述方波信号。

这种表达式通常包含了以下关键要素：信号的振幅（即高电平和低电平的差值）、
信号的周期（即高电平和低电平的持续时间）、信号的占空比（即高电平的持续时间与周期的比值）等等。

方波信号的表达式可以用简洁的数学符号来表示这些要素，使得我们可以清晰地了解方波信号的特征。

另一种常见的方波信号表达式是使用傅里叶级数展开来表示方波信号。

根据傅里叶级数的理论，任何周期性信号都可以由一系列正弦和余弦函数的和来表示。

因此，方波信号也可以通过傅里叶级数展开得到其表达式。

这样的表达式包含了方波信号的基波频率以及一系列谐波频率的振幅和相位信息。

方波信号表达式在工程学、电子学和信号处理等领域具有重要应用。

通过对方波信号的表达式进行分析和处理，我们可以深入理解方波信号的特性，并根据需
要进行信号的合成、解析、滤波等操作。

方波信号表达式的研究与应用对于数字通信、电路设计、控制系统等方面具有重要意义，为我们更好地理解和利用方波信号提供了理论基础和实用工具。