最新惠州一中级高一年级下学期分班考试数学试卷

广东省惠州市惠东县惠东高级中学2024届高一数学第二学期期末学业水平测试模拟试题考生须知： 1．全卷分选择题和非选择题两部分，全部在答题纸上作答。

选择题必须用2B 铅笔填涂；非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。

2．请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。

3．保持卡面清洁，不要折叠，不要弄破、弄皱，在草稿纸、试题卷上答题无效。

一、选择题：本大题共10小题，每小题5分，共50分。

在每个小题给出的四个选项中，恰有一项是符合题目要求的 1．关于x 的方程sin 26x m π⎛⎫+= ⎪⎝⎭在[0,]π内有相异两实根，则实数m 的取值范围为（ ）A ．31,42⎡⎤⎢⎥⎣⎦ B ．31,42⎡⎫⎪⎢⎪⎣⎭C ．11,42⎡⎫⎪⎢⎣⎭D ．11,42⎡⎤⎢⎥⎣⎦2．《九章算术》是我国古代的数学名著，书中有如下问题：“今有五人分五钱，令上二人所得与下三人等．问各得几何．”其意思为“已知甲、乙、丙、丁、戊五人分5钱，甲、乙两人所得与丙、丁、戊三人所得相同，且甲、乙、丙、丁、戊所得依次成等差数列．问五人各得多少钱？”（“钱”是古代的一种重量单位）．这个问题中，甲所得为（ ） A ．54钱 B ．43钱 C ．32钱 D ．53钱 3．圆的半径是6cm ，则15︒的圆心角与圆弧围成的扇形面积是（ ） A ．22cm πB ．2cm πC ．232cm πD ．23cm π4．如图，,A B 两点为山脚下两处水平地面上的观测点，在,A B 两处观察点观察山顶点P 的仰角分别为,αβ，若1tan 3α=，45β=，且观察点,A B 之间的距离比山的高度多100米，则山的高度为（ ）A ．100米B ．110米C ．120米D ．130米5．已知非零向量a ，b 满足2a b =，且()a b b -⊥，则a 与b 的夹角为( )6．唐代诗人李颀的诗《古从军行》开头两句说：“白日登山望烽火，黄昏饮马傍交河.”诗中隐含着一个有趣的数学问题——“将军饮马”问题，即将军在观望烽火之后从山脚下某处出发，先到河边饮马后再回到军营，怎样走才能使总路程最短？在平面直角坐标系中，设军营所在位置为(2,0)B -，若将军从山脚下的点(2,0)A 处出发，河岸线所在直线方程为3x y +=，则“将军饮马”的最短总路程为（ ） A ．4B ．5C ．26D ．327．已知不同的两条直线m ，n 与不重合的两平面α，β，下列说法正确的是（ ） A ．若m n ，m α，则n α B ．若m α，αβ∥，则m β C ．若m n ，m α⊥，则n α⊥ D ．若m n ⊥，m α⊥，则n α⊥ 8．以下说法正确的是（ ） A ．零向量与单位向量的模相等 B ．模相等的向量是相等向量 C ．已知,a b 均为单位向量，若12a b ⋅=，则a 与b 的夹角为60︒ D ．向量AB 与向量CD 是共线向量，则,,,A B C D 四点在一条直线上 9．设A B C D ，，，是空间四个不同的点，在下列命题中，不正确的是 A ．若AC 与BD 共面，则AD 与BC 共面B ．若AC 与BD 是异面直线，则AD 与BC 是异面直线 C ．若AB =AC DB ，=DC ，则AD BC ⊥ D ．若AB = AC DB ，=DC ，则AD =BC10．一块各面均涂有油漆的正方体被锯成27个大小相同的小正方体，若将这些小正方体均匀地搅混在一起，从中任意取出一个，则取出的小正方体两面涂有油漆的概率是( ) A ．B ．C ．D ．二、填空题：本大题共6小题，每小题5分，共30分。

2023-2024学年广东省惠州中学高一（下）期中数学试卷一、单选题：本题共8小题，每小题5分，共40分。

在每小题给出的选项中，只有一项是符合题目要求的。

1.已知集合A ={−2,−1,0,1,2}，B ={x|lnx >0}，则A ∩B =( )A. {1}B. {2}C. {−2,2}D. {−1,0,1}2.已知α，β是平行四边形的两个内角，则“α=β”是“sinα=sinβ”的( )A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件3.已知互相垂直的平面α，β交于直线l ，若直线m ，n 满足m//α，n ⊥β，则( )A. m//lB. m//nC. n ⊥lD. m ⊥n 4.如图，在△ABC 中，AN =12NC ，P 是BN 上的一点，若AP =(m +13)AB +19AC ，则实数m 的值为( )A. 19B. 29C. 23D. 135.若函数f(x)={x 2−2ax +1,x >1ax,x ≤1在其定义域内是一个单调递增函数，则实数a 的取值范围是( )A. (0,1]B. (0,23]C. [0,1]D. [0,23]6.已知一个圆锥的底面半径为3，其侧面积是底面积的2倍，则圆锥的体积为( )A. 6πB. 6 3πC. 9 3πD. 12π7.心理学家有时用函数L(t)=A(1−e −kt )测定在时间t(单位：min)内能够记忆的量L ，其中A 表示需要记忆的量，k 表示记忆率．假设一个学生需要记忆的量为200个单词，此时L 表示在时间t 内该生能够记忆的单词个数．已知该生在5min 内能够记忆20个单词，则k 的值约为( )(ln0.9≈−0.105,ln0.1≈−2.303)A. 0.021B. 0.221C. 0.461D. 0.6618.如图，O 是锐角三角形ABC 的外心，角A ，B ，C 所对的边分别为a ，b ，c ，且A =π3，若cosB sinCAB +cosCsinB AC =2m AO ，则m =( )A. 12 B. 22C. 32D. 1二、多选题：本题共3小题，共18分。

高一下学期期中考试数学试卷一．选择题(每题5分)1．在△ABC 中，a ＝3，b ＝7，c ＝2，那么B 等于（） 2．A ．30°B ．45°C ．60°D ．120°2．在等比数列{a n }中，a 2＝8，a 5＝64，则公比q 为（ ）A ．2B ．3C ．4D ．83．等差数列{}n a 的前n 项和为n S ，若＝则432,3,1S a a == （ ）A ．12B ．10C ．8D ．64．已知a +b >0，b <0，那么a 、b 、－a 、－b 的大小关系是（） A ．a >b >－b >－a B ．a >－b >－a >bC ．a >－b >b >－aD ．a >b >－a >－b5．若10=+<<b a b a 且，则下列四个数中最大的是 （）Ａ．21Ｂ．22b a + Ｃ．ab 2 Ｄ．a6.由11a =，3d =确定的等差数列{}n a ，当298n a =时，序号n 等于（ ）Ａ．99 Ｂ．100Ｃ．96Ｄ．1017.在△ABC 中，∠A=，AB=2，且△ABC 的面积为，则边AC 的长为（ ）A ．1B ．C ．2D ．38．各项为正的等比数列{a n }中，a 2•a 8=16，则a 5=（） A ．4 B ．2 C ．1 D ．89．利用斜二测画法得到： ① 三角形的直观图是三角形；② 平行四边形的直观图是平行四边形； ③ 正方形的直观图是正方形； ④ 菱形的直观图是菱形． 以上结论，正确的是（ ）Ａ．①② Ｂ．① Ｃ．③④ Ｄ．①②③④10．找出图1－3－12中三视图所对应的实物图形是( )图1－3－1211．如图１所示，空心圆柱体的正视图是（ ）12．数列{}n a 的前n 项和为n S ，若1(1)n a n n =+，则5S 等于（ ）A ．1B ．56C ．16D ．13013．设x>0,则xx y 133++=的最小值为（ ）Ａ．3 Ｂ．233+ Ｃ．323+ Ｄ．－114．在△ABC 中，三内角A 、B 、C 的对边分别是a 、b 、c ．若4a 2=b 2+c 2+2bc ，sin 2A=sinB•sinC，则△ABC 的形状的形状为（）A. 等边三角形B. 等腰三角形C. 直角三角形D.等腰直角三角形二．填空题（每题5分）15．已知11a =，111n n a a -=+(2)n ≥，则5a ＝_____________．16．若关于x 的不等式mx x x >+-2212的解集是{}20|<<x x ，则实数m 的值是_____________．17.已知等差数列{}n a 的前三项为32,1,1++-a a a ，则此数列的通项公式为________ .18. 已知数列的前n 项和是, 则数列的通项=n a .三．解答题19. （本题满分10分）求下列关于x 的不等式的解集：(1)－x 2＋7x ＞6；(2) 3x 2＋4x+ 2＞0；20.（本题满分12分）已知A ，B ，C 为△ABC 的三个内角，且其对边分别为a ，b ，c ，若222a cb b c =++ (1)求A ；(2)若a ＝23，b ＋c ＝4，求△ABC 的面积．.21.（本题满分12分）一个几何体的三视图如图所示（单位：m ），求该几何体的体积和表面积。

高一下学期期中考试数学试卷一．选择题(每题5分)1．在△ABC 中，a ＝3，b ＝7，c ＝2，那么B 等于（） 2．A ．30°B ．45°C ．60°D ．120°2．在等比数列{a n }中，a 2＝8，a 5＝64，则公比q 为（ ）A ．2B ．3C ．4D ．83．等差数列{}n a 的前n 项和为n S ，若＝则432,3,1S a a == （ ）A ．12B ．10C ．8D ．64．已知a +b >0，b <0，那么a 、b 、－a 、－b 的大小关系是（） A ．a >b >－b >－a B ．a >－b >－a >bC ．a >－b >b >－aD ．a >b >－a >－b5．若10=+<<b a b a 且，则下列四个数中最大的是 （）Ａ．21Ｂ．22b a + Ｃ．ab 2 Ｄ．a6.由11a =，3d =确定的等差数列{}n a ，当298n a =时，序号n 等于（ ）Ａ．99 Ｂ．100Ｃ．96Ｄ．1017.在△ABC 中，∠A=，AB=2，且△ABC 的面积为，则边AC 的长为（ ）A ．1B ．C ．2D ．38．各项为正的等比数列{a n }中，a 2•a 8=16，则a 5=（） A ．4 B ．2 C ．1 D ．89．利用斜二测画法得到： ① 三角形的直观图是三角形；② 平行四边形的直观图是平行四边形； ③ 正方形的直观图是正方形； ④ 菱形的直观图是菱形． 以上结论，正确的是（ ）Ａ．①② Ｂ．① Ｃ．③④ Ｄ．①②③④10．找出图1－3－12中三视图所对应的实物图形是( )图1－3－1211．如图１所示，空心圆柱体的正视图是（ ）12．数列{}n a 的前n 项和为n S ，若1(1)n a n n =+，则5S 等于（ ）A ．1B ．56C ．16D ．13013．设x>0,则xx y 133++=的最小值为（ ）Ａ．3 Ｂ．233+ Ｃ．323+ Ｄ．－114．在△ABC 中，三内角A 、B 、C 的对边分别是a 、b 、c ．若4a 2=b 2+c 2+2bc ，sin 2A=sinB•sinC，则△ABC 的形状的形状为（）A. 等边三角形B. 等腰三角形C. 直角三角形D.等腰直角三角形二．填空题（每题5分）15．已知11a =，111n n a a -=+(2)n ≥，则5a ＝_____________．16．若关于x 的不等式mx x x >+-2212的解集是{}20|<<x x ，则实数m 的值是_____________．17.已知等差数列{}n a 的前三项为32,1,1++-a a a ，则此数列的通项公式为________ .18. 已知数列的前n 项和是, 则数列的通项=n a .三．解答题19. （本题满分10分）求下列关于x 的不等式的解集：(1)－x 2＋7x ＞6；(2) 3x 2＋4x+ 2＞0；20.（本题满分12分）已知A ，B ，C 为△ABC 的三个内角，且其对边分别为a ，b ，c ，若222a cb b c =++ (1)求A ；(2)若a ＝23，b ＋c ＝4，求△ABC 的面积．.21.（本题满分12分）一个几何体的三视图如图所示（单位：m ），求该几何体的体积和表面积。

2025届广东省惠州一中高考数学必刷试卷注意事项1．考生要认真填写考场号和座位序号。

2．试题所有答案必须填涂或书写在答题卡上，在试卷上作答无效。

第一部分必须用2B 铅笔作答；第二部分必须用黑色字迹的签字笔作答。

3．考试结束后，考生须将试卷和答题卡放在桌面上，待监考员收回。

一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

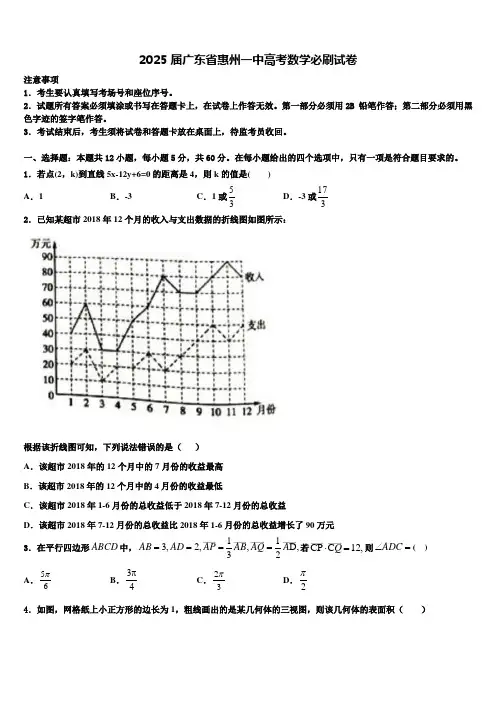
1．若点(2，k)到直线5x-12y+6=0的距离是4，则k的值是( )A．1 B．-3 C．1或53D．-3或1732．已知某超市2018年12个月的收入与支出数据的折线图如图所示：根据该折线图可知，下列说法错误的是（）A．该超市2018年的12个月中的7月份的收益最高B．该超市2018年的12个月中的4月份的收益最低C．该超市2018年1-6月份的总收益低于2018年7-12月份的总收益D．该超市2018年7-12月份的总收益比2018年1-6月份的总收益增长了90万元3．在平行四边形ABCD中，113,2,,D,32AB AD AP AB AQ A====若CP C12,Q⋅=则ADC∠=( )A．56πB．34πC．23πD．2π4．如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则该几何体的表面积（）A ．623+B ．622+C ．442+D ．443+5． “1sin 2x =”是“2()6x k k Z ππ=+∈”的（ ） A ．充分不必要条件 B ．必要不充分条件 C ．充要条件D ．既不充分也不必要条件6．抛物线()220y px p =>的准线与x 轴的交点为点C ，过点C 作直线l 与抛物线交于A 、B 两点，使得A 是BC 的中点，则直线l 的斜率为（ ） A ．13±B ．223±C ．±1D ．37．已知数列{}n a 中，112,()1,n n n a n a a a n N *+=-=+∈ ，若对于任意的[]*2,2,a n N ∈-∈，不等式21211n a t at n +<+-+恒成立，则实数t 的取值范围为（ ） A ．(][),21,-∞-⋃+∞ B ．(][),22,-∞-⋃+∞ C ．(][),12,-∞-⋃+∞D ．[]2,2-8．设F 为抛物线24x y =的焦点，A ，B ，C 为抛物线上三点，若0FA FB FC ++=，则|||||FA FB FC ++=（ ）. A ．9B ．6C ．38D ．3169．设f (x )是定义在R 上的偶函数，且在(0,+∞)单调递减，则（ ） A ．0.30.43(log 0.3)(2)(2)f f f -->>B ．0.40.33(log 0.3)(2)(2)f f f -->>C ．0.30.43(2)(2)(log 0.3)f f f -->> D ．0.40.33(2)(2)(log 0.3)f f f -->>10．已知命题p ：x ∀∈R ，210x x -+<；命题 q ：x ∃∈R ，22x x >，则下列命题中为真命题的是（ ） A ．p q ∧B ．p q ⌝∧C ．p q ∧⌝D ．p q ⌝∧⌝11．已知15455,log 5,log 2a b c ===，则,,a b c 的大小关系为（ ）A ．a b c >>B ．a c b >>C ．b a c >>D ．c b a >>12．过双曲线()222210,0x y a b a b-=>>的左焦点作倾斜角为30的直线l ，若l 与y 轴的交点坐标为()0,b ，则该双曲线的标准方程可能为（ ）A ．2212x y -=B ．2213x y -=C ．2214x y -=D ．22132x y -=二、填空题：本题共4小题，每小题5分，共20分。

广东省惠州市市第一中学高一数学理联考试卷含解析一、选择题：本大题共10小题，每小题5分，共50分。

在每小题给出的四个选项中，只有是一个符合题目要求的1. 如果点位于第三象限，那么角所在象限是（）Ａ.第一象限 B.第二象限 C.第三象限 D.第四象限参考答案：B略2. 角的始边在轴正半轴、终边过点，且，则y的值为（）A.3B. 1C. ±3D. ±1参考答案：C略3. 将函数的图象上所有点向左平移个单位，再将所得的图象的所有点的横坐标伸长到原来的2倍（纵坐标不变），得到的图象对应的解析式是（）A. B.C. D.参考答案：A由题意，将函数的图象上所有点向左平移个单位，得到，将得到的图象的所有点的横坐标伸长到原来的2倍（纵坐标不变），得到.故答案为A.4. 设集合A={x|x2+2x﹣3＞0}，集合B={x|x2﹣2ax﹣1≤0，a＞0}．若A∩B中恰含有一个整数，则实数a的取值范围是（）A．B．C．D．（1，+∞）参考答案：B【考点】交集及其运算．【专题】计算题．【分析】先求解一元二次不等式化简集合A，B，然后分析集合B的左端点的大致位置，结合A∩B中恰含有一个整数得集合B的右端点的范围，列出无理不等式组后进行求解．【解答】解：由x2+2x﹣3＞0，得：x＜﹣3或x＞1．由x2﹣2ax﹣1≤0，得：．所以，A={x|x2+2x﹣3＞0}={x|x＜﹣3或x＞1}，B={x|x2﹣2ax﹣1≤0，a＞0}={x|}．因为a＞0，所以a+1＞，则且小于0．由A∩B中恰含有一个整数，所以．即，也就是．解①得：a，解②得：a．所以，满足A∩B中恰含有一个整数的实数a的取值范围是．故选B．【点评】本题考查了交集及其运算，考查了数学转化思想，训练了无理不等式的解法，求解无理不等式是该题的一个难点．此题属中档题．5. 若三角形的三条高线长分别为12，15，20，则此三角形的形状为（）A．锐角三角形 B．直角三角形 C．钝角三角形 D．形状不确定参考答案：B6. 令a=60.7，b=0.76，c=log0.76，则三个数a、b、c的大小顺序是（）A．b＜c＜a B．b＜a＜c C．c＜a＜b D．c＜b＜a参考答案：D【考点】指数函数的单调性与特殊点．【分析】由指数函数和对数函数的图象可以判断a、b、c和0 和1的大小，从而可以判断a、b、c的大小．【解答】解：由指数函数和对数函数的图象可知：a＞1，0＜b＜1，c＜0，所以c＜b＜a故选D7. 已知方程|x|－ax－1＝0仅有一个负根，则a的取值范围是()A．a<1 B．a≤1 C．a>1 D．a≥1参考答案：D8. 已知集合M={x|y=}，集合N={y|y=x2-2x+1,x∈R},则M∩N=( ).A.{x|x≤2}B.{x|x≥2}C.{x|0≤x≤2}D.参考答案：C9. 函数y=的定义域为（）A．（，+∞） B．［1，+∞ C．（，1 D．（－∞，1）参考答案：C10. （5分）某三棱锥的三视图如图所示，该三梭锥的表面积是（）A．60+12B．56+12C．30+6D．28+6参考答案：C考点：由三视图求面积、体积．专题：空间位置关系与距离．分析：通过三视图复原的几何体的形状，利用三视图的数据求出几何体的表面积即可．解答：三视图复原的几何体是底面为直角边长为4和5的三角形，一个侧面垂直底面，且此侧面为等腰三角形，三棱锥的高为4，底边长为5，如图所示．所以S底=×4×5=10，S后=×5×4=10，S右=×4×5=10，S左=×2×=6．几何体的表面积为：S=S底+S后+S右+S左=30+6．故选C．点评：本题考查三视图与几何体的关系，注意表面积的求法，考查空间想象能力计算能力．二、填空题:本大题共7小题,每小题4分,共28分11. 在△ABC中，点D在线段BC上，且，，则△ABC面积的最大值为__________．参考答案：【分析】在、中通过互补的两个角做为纽带，根据它们的余弦和为零，构造等式，通过这个等式，利用基本不等式，可以得到两边乘积的最大值，最后根据面积公式，可求出面积的最大值。

惠州市2023-2024学年度第二学期期末质量检测高一数学参考答案与评分细则一、单项选择题：本题共8小题，每小题满分5分，共40分．题号12345678答案CDACBDDA1．【解析】由题得()()()()231151+12i i i z i i ----==-，所以z 对应的点的坐标是15,22⎛⎫-- ⎪⎝⎭，故选C ．2．【解析】零向量的方向是任意的，故A 错误；相等向量要求方向相同且模长相等，共线向量不一定是相等向量，故B 错误；当0λ<，则向量a 与a λ方向相反，故C 错误；对于D ：单位向量的模为1，都相等，故D 正确.3．【解析】因为1238,,,,x x x x 的平均数是10，方差是10，所以123832,32,32,,32x x x x ++++ 的平均数是310232⨯+=，方差是231090⨯=.故选A ．4．【解析】【方法一】向量a 在b方向上的投影向量为()()22cos ,1,04a b b b ba ab b b⋅<>⋅===；【方法二】数形结合，由图易得选项C 正确，故选C.5．【解析】样本中高中生的人数比小学生的人数少20，所以5320543543n n -=++++，解得120n =，故选B ．6．【解析】对于选项A ，易得,αβ相交或平行，故选项A 错误；对于选项B ，,m n 平行或异面，故选项B 错误；对于选项C ，当直线,m n 相交时，//αβ才成立，故选项C 错误；对于选项D ，由线面垂直的性质可知正确，故选D.7．【解析】对于选项A ，因为掷两颗骰子，两个点数可以都是偶数，也可以都是奇数，还可以一奇一偶，即一次试验，事件A 和事件B 可以都不发生，所以选项A 错误；对于选项B ，因为C D ⋂即两个点数都是偶数，即A 与C D ⋂可以同时发生，所以选项B 错误；对于选项C ，因为331()664P B ⨯==⨯，333()1664P D⨯=-=⨯，又()0P BD =，所以()()()P BD P B P D ≠，故选项C 错误；对于选项D ，因为()1P C D = ，所以C D =Ω ，因为必然事件与任意事件相互独立，所以B 与C D ⋃是相互独立事件，故选D ．8．【解析】因为11AC CB =，AC BC =，取AB 中点D ，则1C DC ∠为二面角1C AB C --的平面角，所以14C DC π∠=．在1Rt C DC ∆中，可得112,CD CC C D ===，又1182V AB CD CC =⋅⋅=，解得4AB =，所以AC ==.由1111A ABC B AA C V V --=得1111133ABC AA C S h S BC ∆∆⋅=⋅，代入数据求解得到点1A 到平面1ABC的距离h =，故选A ．二、多项选择题：本题共3小题，每小题满分6分，共18分．在每小题给出的四个选项中，有多项符合题目要求．全部选对得6分，部分选对得部分分，有选错的得0分．题号题9题10题11全部正确选项ABCBCAD9．【解析】依题意球的表面积为24πR ，圆柱的侧面积为22π24πR R R⨯⨯=，所以AC 选项正确；圆锥的侧面积为2πRR ⨯=，所以B 选项正确；圆锥的表面积为(2222π1π4πR R R R +=<，圆柱的表面积为2224π2π6πR R R +=，所以D 选项错误．故选ABC ．10．【解析】由1i z i +=-得22z =，故选项A 错误；根据复数的运算性质，易知BC 正确；根据22z -≤的几何意义求解，点Z 在以圆心为()2,0，半径为2的圆内及圆周上，所以集合M 所构成区域的面积为4π，所以D 选项错误．故选BC ．11．【解析】对于选项A ，若60A =︒，2a =，则2222cos a b c bc A =+-，即224b c bc bc =+-≥，当且仅当2b c ==时，取等号，所以1sin 2ABC S bc A ==≤△，所以ABC 故选项A正确，B 错误．对于选项C ，要使满足条件的三角形有且只有两个，则sin b A a b <<，因为4a b==，所以4sin A <πsin 0,2A A ⎛⎫∈ ⎪⎝⎭，所以03A π<<.故选项C 错误.对于选项D ，()cos cos a b c A B +=+等价于cos cos a b A B c +=+，即22222222a b b c a a c bc bc ac++-+-=+，对该等式通分得到()()()2222222ab a b a b c a b a c b +=+-++-，即2222322322a b ab ab ac a a b bc b +=+-++-，即3322220a b a b ab ac bc +++--=．这即为()()()()2220a b a ab b ab a b c a b +-+++-+=，由0a b +≠知该等式即为2220a b c +-=．从而条件等价于2220a b c +-=且1c =，从而该三角形内切圆半径)121122ABC ab S ab ab r a b c a b c a b ab ===++++++ 当且仅当2a b ==时等号成立，从而0r <≤2213πππ24S r ⎛⎫-=≤= ⎪ ⎪⎝⎭内切圆．验证知当2a b ==时，等号成立，所以该三角形的内切圆面积的最大值是3π4-，所以选项D 正确．故选AD ．三、填空题：本题共3小题，每小题5分，共15分；其中第14题的第一个空2分，第二个空3分．12．71513．a b <【注：也可以是b a >，0b a ->或a 小于b 】14．2；412．【解析】已知甲、乙两人独立的解同一道题，甲，乙解对题的概率分别是23，35，恰好有1人解对题的概率是22137353515⨯+⨯=.【注：写成有限小数不给分】13．【解析】由平均数在“拖尾”的位置，可知a b <．14．【解析】（1）13E ABC ABC V S EB -∆=⋅，在ABC ∆中，由余弦定理可知，1cos 8BAC ∠=，所以sin 8BAC ∠==，所以113772413282E ABC V -=⨯⨯⨯⨯⨯=.（2）作BH AC ⊥，垂足为H ，作1111B H AC ⊥，垂足为H 1，易证棱1BB 在平面11ACC A 上的射影为1HH ，则点E 在平面11ACC A 上的射影1E 在线段1HH 上，由（1）知，1cos 8BAC ∠=，故128AH AH AB ==，解得14AH =，故BH =，则1EE =，设AF 的中点为1Q ，外接球的球心为Q ，半径为1R ，则1QQ ⊥平面11ACC A ，即11//QQ EE ，在1Rt FQQ中，222211QF R QQ ==+①，又因为222211114QE R QQ Q E ⎛⎫==-+ ⎪ ⎪⎝⎭②，由①②可得211131216QQ Q E =+，所以当11Q E 取最小值时，1QQ 最小，即1R 最小，此时111Q E HH ⊥，因为1Q 是AF 的中点，则1E 是1HH 的中点，则E 是棱1BB 的中点．因为11//AA BB ，所以直线EF 与1BB 所成角即为直线EF 与1AA 所成角．由1111cos 8A CB =∠，再由余弦定理可得1B F 因为11EB =，所以EF =11cos 4E FEB B EF =∠=．四、解答题：本题共5小题，共77分．解答应写出文字说明、证明过程或演算步骤．15．（本小题满分13分，其中第（1）小问6分，第（2）小问7分。

广东省惠州市高一下学期开学数学试卷姓名:________ 班级:________ 成绩:________一、选择题 (共12题；共24分)1. （2分） (2018高一上·吉林期中) 函数f(x)＝（e为自然对数的底数）的值域为（）A . (－1，1)B . (－1，＋∞)C . (－∞，1)D . (－1，0)∪(0，1)2. （2分）已知集合，则下列式子表示正确的有（）①②③④A . 1个B . 2个C . 3个D . 4个3. （2分）下列各组函数是同一函数的是（）①与；②与；③与；④与。

A . ①②B . ①③C . ②③④D . ①④4. （2分） (2016高一上·慈溪期中) 函数的定义域是（）A . （1，+∞）B . （1，2]C . （2，+∞）D . （﹣∞，2）5. （2分） (2016高一上·济南期中) 若，则化简的结果是（）A .B .C .D .6. （2分） (2017高一上·定远期中) 设，则f[f（﹣1）]=（）A . 1B . 2C . 4D . 87. （2分） (2016高一下·永年期末) 已知函数f（x）= sinωx+cosωx（ω＞0）的图象与x轴交点的横坐标构成一个公差为的等差数列，把函数f（x）的图象沿x轴向左平移个单位，得到函数g（x）的图象．若在区间[0，π]上随机取一个数x，则事件“g（x）≥ ”发生的概率为（）A .B .C .D .8. （2分） y1＝2x ， y2＝x2 ， y3＝log2x ，当2<x<4时，有（）A . y1>y2>y3B . y2>y1>y3C . y1>y3>y2D . y2>y3>y19. （2分） (2017高二上·黄山期末) 下列命题中正确的是（）A . 若p∨q为真命题，则p∧q为真命题B . 若直线ax+y﹣1=0与直线x+ay+2=0平行，则a=1C . 若命题“∃x∈R，x2+（a﹣1）x+1＜0”是真命题，则实数a的取值范围是a＜﹣1或a＞3D . 命题“若x2﹣3x+2=0，则x=1或x=2”的逆否命题为“若x≠1或x≠2，则x2﹣3x+2≠0”10. （2分）用反证法证明命题：“三个连续正整数a，b，c中至少有一个能被2整除”时，要做的假设是（）A . 假设三个连续正整数a，b，c都不能被2整除B . 假设三个连续正整数a，b，c都能被2整除C . 假设三个连续正整数a，b，c至多有一个能被2整除D . 假设三个连续正整数a，b，c至多有两个能被2整除11. （2分） (2015高一上·洛阳期末) 在四棱锥P﹣ABCD中，各侧面是全等的等腰三角形，腰长为4且顶角为30°，底面是正方形（如图），在棱PB，PC上各有一点M，N，且四边形AMND的周长最小，点S从A出发依次沿四边形AM，MN，ND运动至点D，记点S行进的路程为x，棱锥S﹣ABCD的体积为V（x），则函数V（x）的图象是（）A .B .C .D .12. （2分）函数y＝5＋sin22x的最小正周期为（）A . 2πB . πC .D .二、填空题： (共4题；共5分)13. （1分） (2016高一下·武邑期中) 已知圆锥的轴截面是一个边长为2的正三角形，则圆锥的侧面积等于________．14. （1分） (2016高一上·东海期中) lg +2lg2﹣（）﹣1=________．15. （2分） (2017高一上·海淀期末) 已知函数f（x）=|ax﹣1|﹣（a﹣1）x（1）当a= 时，满足不等式f（x）＞1的x的取值范围为________；若函数f（x）的图象与x轴没有交点，则实数a的取值范围为________．16. （1分）如果y=f（x）的定义域为R，对于定义域内的任意x，存在实数a使得f（x+a）=f（﹣x）成立，则称此函数具有“P（a）性质”．给出下列命题：①函数y=sinx具有“P（a）性质”；②若奇函数y=f（x）具有“P（2）性质”，且f（1）=1，则f（2015）=1；③若函数y=f（x）具有“P（4）性质”，图象关于点（1，0）成中心对称，且在（﹣1，0）上单调递减，则y=f（x）在（﹣2，﹣1）上单调递减，在（1，2）上单调递增；④若不恒为零的函数y=f（x）同时具有“P（0）性质”和“P（3）性质”，且函数y=g（x）对，都有|f（x1）﹣f（x2）|≥2成立，则∀x1 ，x2∈R，都有|f（x1）﹣f（x2）|≥2成立．其中正确的是________ （写出所有正确命题的编号）．三、解答题： (共6题；共60分)17. （5分） (2016高二上·怀仁期中) 已知△ABC的三个顶点A（﹣1，0），B（1，0），C（3，2），其外接圆为⊙H．若直线l过点C，且被⊙H截得的弦长为2，求直线l的方程．18. （10分）(2018·广州模拟) 如图，多面体ABCDEF中，四边形ABCD为矩形，二面角A-CD-F为60°，DE∥CF，CD⊥DE，AD=2，DE=DC=3，CF=6.（1）求证：BF∥平面ADE；（2）在线段CF上求一点G，使锐二面角B-EG-D的余弦值为 .19. （10分） (2019高一下·延边月考) 已知函数在区间上单调，当时，取得最大值5，当时，取得最小值-1.（1）求的解析式（2）当时，函数有8个零点，求实数的取值范围。