立体几何中向量法常用公式.
- 格式:doc
- 大小:209.00 KB
- 文档页数:2

高中数学立体几何向量公式
在三维空间中,向量有着相应的公式。
第一个公式是向量a加向量b,即a+b=a+b。
这表示将两个向量相加,得到一个新的向量。
下一个公式是a×b,它表示两个向量的点积,这意味着它们的方向是相反的,但它们的大小是不同的。
还有另一个公式叫平行向量,它表示两个向量具有相同的方向。
它可以写成:a∥b,这意味着它们之间的另一个角度被视为0度。
另外,向量也有一个公式,它可以用来描述两个向量的向量积,这是一个形状向量,表示另一个向量的方向或大小与其相似。
最后,还有一个叫作法向量的公式,它表示了一个向量和一个平面的关系,这被用来描述法线的方向,它可以写为n=b-a。
总而言之,立体几何中向量的公式涉及加减、点积和叉积等内容,是高中学习数学中十分重要的一部分。
了解并掌握这些公式有助于学生更好地理解数学知识,更好的运用到学习中去。



空间向量与立体几何公式一、空间向量1、空间向量是一种简单的数学表达形式,表示一组相同类型数据成员之间的关系。
它可以描述空间中的每个点与另一个点之间的连接情况,而连接情况是由三个不同的坐标表示的。
换言之,空间向量就是描述空间中一个点到另一个点的方向及距离,作为一种数学实体而存在的。
2、空间向量可以用一个有向箭头来表示,并用数学记号标注出来。
通常来说,它的数学记号是表示坐标系中的另一个点在第一个点的坐标上的偏移量,如a→b表示b点在a点上的偏移量。
3、空间向量形式可以表示一条从原点到某个点的路径,通过它可以确定在x、y和z轴上的平移量,即偏移量,从而避免了我们有时在空间中运行物体时会误解运动方向的困难。
从更宏观的角度来说,空间向量可以用来表示以位置、速度和加速度等。
二、立体几何公式1、立体几何是几何学分支之一,它学习的内容是空间中的点、线、面和体的特性、关系及其变化规律,其中关于立体图形的内容被称为立体几何。
立体几何的定义是关于空间中的点、线、面和体的研究,以及它们之间的关系,其中主要考虑的就是位置、形状、大小以及一般的空间概念。
2、立体几何公式包括:立体几何定义、立体几何变换、立体几何性质、其他立体几何相关概念以及三角几何相关公式。
例如,立体几何定义涉及的公式有:空间中的点的位置关系(a-b=c),线的距离关系(L=1/2×Z1×Z2),面的面积关系(S=1/2×Z1×Z2×cosX),以及球体表面积(S=4×π×R2)等公式。
3、另外,立体几何公式还包括三角几何公式,它主要涉及到角度、正弦、余弦、正切、反正切等相关公式。
这些公式用来解决各种形状三角形以及其他更复杂的立体图形以及相关空间距离关系的问题。


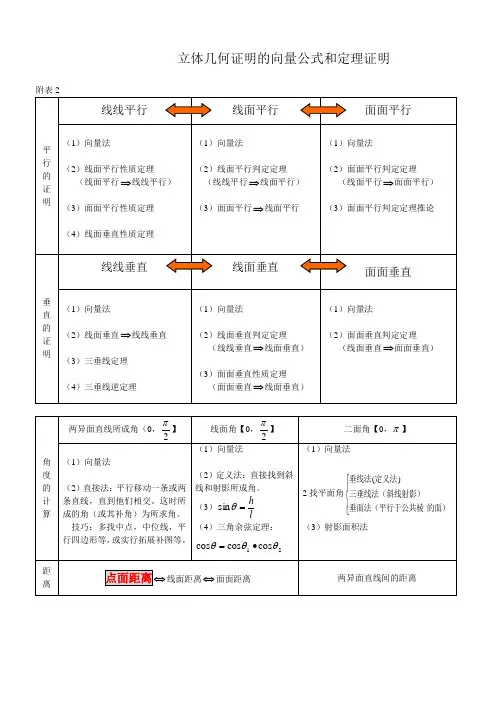
立体几何证明的向量公式和定理证明立体几何中的向量公式和定理证明非常多,下面仅列举其中几个常见的向量公式和定理的证明。
1.向量叉乘的模长公式证明:对于两个三维向量A=(a1,a2,a3)和B=(b1,b2,b3),它们的叉乘C=A×B定义为C=(a2b3-a3b2,a3b1-a1b3,a1b2-a2b1)。
根据向量的定义,我们有C,^2=(a2b3-a3b2)^2+(a3b1-a1b3)^2+(a1b2-a2b1)^2=(a2^2b3^2-2a2a3b2b3+a3^2b2^2)+(a3^2b1^2-2a1a3b1b3+a1^2b3^2)+(a1^2b2^2-2a1a2b1b2+a2^2b1^2)=a2^2b3^2+a3^2b1^2+a1^2b2^2-2a2a3b2b3-2a1a3b1b3-2a1a2b1b2+a3^2b2^2+a1^2b3^2+a2^2b1^2-2a1a2b1b2-2a2a3b2b3+a1^2b2^2=a1^2(b2^2+b3^2)+a2^2(b1^2+b3^2)+a3^2(b1^2+b2^2)-2(a1a2b1b2+a2a3b2b3+a1a3b1b3)=a1^2,B,^2+a2^2,B,^2+a3^2,B,^2-2(a1a2b1b2+a2a3b2b3+a1a3b1b3)=(a1^2+a2^2+a3^2),B,^2=,A,^2,B,^2因此,可以得出,C, = ,A × B, = ,A,B,sinθ,其中θ为A和B的夹角。
2.向量线性组合的余子定理证明:设有n个非零向量v1, v2, ..., vn,如果它们的线性组合为零向量,即存在一组不全为零的实数c1, c2, ..., cn,使得c1v1 + c2v2 + ...+ cnvn = 0,则对于其中任意一个向量,它的余子向量与其余子式满足如下关系:v1 × (v2 × ... × vn) = (v1 · vn) (v2 × ... × vn) -(v1 · vn-1)(v2 × ... × vn-1)vn为了证明上述关系,我们可以使用向量叉乘的定义进行展开计算。

二面角向量法公式在咱们学习立体几何的时候,有一个很重要的概念——二面角向量法公式。
这玩意儿可真是个厉害的工具,能帮咱们解决不少难题呢!先来说说啥是二面角。
想象一下,你有两块板子,它们斜着靠在一起,形成的那个“夹角”就是二面角。
要想准确算出这个角的大小,二面角向量法公式就派上用场啦。
公式是这样的:cosθ = |(n1·n2) / (|n1| × |n2|)| ,这里的 n1 和 n2 是两个平面的法向量。
可别被这一堆符号吓到,咱们慢慢捋一捋。
法向量又是啥呢?简单说,就是和平面垂直的向量。
比如说,有一个平面,你总能找到一个向量,它直直地立在这个平面上,那它就是法向量。
我记得我之前教过一个学生,叫小李。
这孩子呀,刚开始接触二面角向量法公式的时候,那叫一个迷糊。
有一次上课,我在黑板上写了一道例题,让大家试着用公式算一下二面角。
小李坐在那儿,抓耳挠腮,半天没动静。
我走过去一看,他连法向量都还没找对。
我就耐心地跟他说:“小李呀,你看这个平面的方程,先把它的系数找出来,然后设法向量是(x,y,z),根据垂直的条件列出方程组,就能求出法向量啦。
”小李似懂非懂地点点头,又埋头苦算了起来。
经过几次这样的耐心指导,小李终于慢慢掌握了窍门。
后来有一次小测验,碰到一道二面角的题目,他刷刷刷几下就把法向量求出来,然后顺利地用公式算出了二面角的大小。
看到他那自信满满的样子,我心里也特别欣慰。
那咱们再回到这个公式。
计算的时候,一定要注意向量的点乘和模长的计算,可别马虎。
有时候一个小数字算错了,整个结果就全错啦。
而且呀,用这个公式的时候,要先判断二面角是锐角还是钝角。
这就需要咱们对图形有一个清晰的认识。
比如说,如果两个法向量的方向都是从二面角内部指向外部,那算出的余弦值就是二面角的余弦值;如果一个从内部指向外部,一个从外部指向内部,那算出的余弦值的相反数才是二面角的余弦值。
总之,二面角向量法公式虽然看起来有点复杂,但只要咱们多做几道题,多琢磨琢磨,就能熟练掌握,让它成为咱们解决立体几何问题的有力武器。



平面向量 坐标运算:(1)设a =11(,)x y ,b =22(,)x y ,则a +b =1212(,)x x y y ++. (2)设a =11(,)x y ,b =22(,)x y ,则a -b =1212(,)x x y y --. (3)设A 11(,)x y ,B 22(,)x y ,则2121(,)AB OB OA x x y y =-=-- . (4)设a =(,),x y R λ∈,则λa =(,)x y λλ. (5)设a =11(,)x y ,b =22(,)x y ,则a ·b =1212()x x y y +.向量内积:a 与b 的数量积(或内积):a ·b =|a ||b |cos θ 两向量的夹角公式:121222221122cos ||||x x y y a b a b x y x y θ+⋅==⋅+⋅+ (a =11(,)x y ,b =22(,)x y ).平面两点间的距离公式:,A B d 222121()()x x y y =-+- (A 11(,)x y ,B 22(,)x y ). 向量的平行与垂直 :设a =11(,)x y ,b =22(,)x y ,且b ≠0 ,则:a ||b 12210x y x y ⇔-=.(交叉相乘差为零) a ⊥b (a ≠0 )⇔ a ·b =012120x x y y ⇔+=.(对应相乘和为零)线段的定比分公式 :设111(,)P x y ,222(,)P x y ,(,)P x y 是线段12P P 的分点,λ是实数,且12PP PP λ= ,则 121211x x x y y y λλλλ+⎧=⎪⎪+⎨+⎪=⎪+⎩⇔121OP OP OP λλ+=+ 直线和圆斜率公式 :2121y y k x x -=-(111(,)P x y 、222(,)P x y ). 直线方程:(1)点斜式 11()y y k x x -=- (直线l 过点111(,)P x y ,且斜率为k ).(2)斜截式 y kx b =+(b 为直线l 在y 轴上的截距).(3)两点式 112121y y x x y y x x --=--(12y y ≠) (111(,)P x y 、222(,)P x y (1212,x x y y ≠≠))(4)截距式 1x y a b+=(a b 、分别为直线的横、纵截距,00a b ≠≠、) (5)一般式 0Ax By C ++=(其中A 、B 不同时为0). 直线0Ax By C ++=的法向量:(,)l A B '= ,方向向量:(,)l B A =-夹角公式:(1)2121tan ||1k k k k α-=+. (111:l y k x b =+,222:l y k x b =+,121k k ≠-) (2)12211212tan ||A B A B A A B B α-=+.(1111:0l A x B y C ++=,2222:0l A x B y C ++=,12120A A B B +≠). 直线12l l ⊥时,直线l 1与l 2的夹角是2π.1l 到2l 的角:(1)2121tan 1k k k k α-=+.(111:l y k x b =+,222:l y k x b =+,121k k ≠-) (2)12211212tan A B A B A A B B α-=+.(1111:0l A x B y C ++=,2222:0l A x B y C ++=,12120A A B B +≠).直线12l l ⊥时,直线l 1到l 2的角是2π. 点到直线的距离 :0022||Ax By C d A B++=+(点00(,)P x y ,直线l :0Ax By C ++=).圆的四种方程:(1)圆的标准方程 222()()x a y b r -+-=. (2)圆的一般方程 220x y Dx Ey F ++++=(224D E F +->0).(3)圆的参数方程 cos sin x a r y b r θθ=+⎧⎨=+⎩.点与圆的位置关系:点00(,)P x y 与圆222)()(r b y a x =-+-的位置关系有三种:2200()()d a x b y =-+-, 则d r >⇔点P 在圆外; d r =⇔点P 在圆上; d r <⇔点P 在圆内.直线与圆的位置关系:直线0=++C By Ax 与圆222)()(r b y a x =-+-的位置关系有三种(22BA C Bb Aa d +++=): 0<∆⇔⇔>相离r d ; 0=∆⇔⇔=相切r d ;0>∆⇔⇔<相交r d . 两圆位置关系的判定方法:设两圆圆心分别为O 1,O 2,半径分别为r 1,r 2,d O O =21,则:条公切线外离421⇔⇔+>r r d ;条公切线外切321⇔⇔+=r r d ;条公切线相交22121⇔⇔+<<-r r d r r ;条公切线内切121⇔⇔-=r r d ;无公切线内含⇔⇔-<<210r r d .立体几何空间中的平行问题线面平行的判定定理:平面外一条直线与此平面内一条直线平行,则该直线与此平面平行。
讲义:立体几何中的向量方法及二面角的平面角求法总结一、几种角的范围1、 _________________________________ 二面角平面角的范围:2、 _________________________________ 线面角的范围:3、 _________________________________ 直线倾斜角范围:4、异面直线夹角范围:_______________5、向量夹角范围:_________________二、立体几何中的向量方法1. 三个重要向量(1) 直线的方向向量:直线的方向向量是指和这条直线平行(或重合)的向量,一条直线的方向向量有 ______ .(2) 平面的法向量:直线I丄平面a取直线I的方向向量,则这个向量叫做平面a的法向量.显然一个平面的法向量有 ____ ,它们是共线向量.(3) 直线的正法向量:直线L:Ax+By+C=O的正法向量为n=(A,B).2. 直线的方向向量与平面的法向量在确定直线和平面位置关系中的应用(1) 直线l i的方向向量为u 1= (a i, b i, c i),直线l2的方向向量为比=(a2, b2, C2).女口果丨1 //丨2,那么U1 // U2? 5=右2? ____________________________ ;女口果丨1丄l2, 那么U1丄U2? U1 U2= 0? ________________⑵直线I的方向向量为u= (a1, b1, C1),平面a的法向量为n= (a2, b2, C2).若I // a 贝U u 丄n? u n = 0? __________________若I 丄a 贝U u // n? u = k n? ______________________(3)平面a的法向量为U1 = (a1, b1, C1),平面B的法向量为u2= (a2, b2, C2).若all B U1 / U2? U1 = k u2? (a1, b1, G)= _________________ ;若a丄B 贝y U1 丄U2? U1 U2= 0? ______________________3. 利用空间向量求空间角(1)求两条异面直线所成的角:设a, b分别是两异面直线I1, I2的方向向量,则(2) 求直线与平面所成的角:设直线I 的方向向量为a ,平面a 的法向量为n ,直线I 与平面a 所成的角为 0,则 si nA |cos 〈 a , n > |=(3) 求二面角的大小:(I )若 AB , CD 分别是二面角a — I — B 的两个半平面内与棱I 垂直的异面直线,则二面角的大 小就是向量AB , CD 的夹角(如图①所示).(H )设n i , n 2分别是二面角a — I — B 的两个半平面a, B 的法向量,贝U 向量n i 与n 2的夹角(或 其补角)的大小就是二面角的大小(如图②③).4. 求点面距:平面a 外一点P 到平面a 的距离为:其中n 为平面a 的法向量,PQ 为平面a 的斜线,Q 为斜足5. 平面法向量的求法设出平面的一个法向量n = (x , y , z),利用其与该平面内的两个不共线向量垂直,即数量积为 0, 列出方程组,两个方程,三个未知数,此时给其中一个变量恰当赋值,求出该方程组的一个非零 解,即得到这个法向量的坐标.注意,赋值不同得到法向量的坐标也不同, 法向量的坐标不唯一.6. 射影面积公式:二面角的平面角为 a ,则cos a=7. 利用空间向量求角要注意的问题(1)异面直线所成的角、直线和平面所成的角、二面角都可以转化成空间向量的夹角来求.⑵空间向量的夹角与所求角的范围不一定相同,如两向量的夹角范围是[0, n,两异面直线所成的角的范围是o , n . (3)用平面的法向量求二面角时,二面角的大小与两平面法向量的夹角有相等和互补两种情况 .三、二面角的平面角的求法1、定义法: 从一条直线出发的两个半平面所组成的图形叫做二面角 ,这条直线叫做二面角的棱,这两个半平面叫做二面角的面,在棱上取点,分别在两面内引两条射线与棱垂直,这两条 垂线所成的角的大小就是二面角的平面角。
立体几何向量投影公式
嘿,咱今天就来聊聊立体几何向量投影公式呀!先来说说向量 a 在向量b 上的投影公式,那就是acosθ呀!比如说,想象一下有个力向量 a 作用在一个物体上,而向量 b 就像是这个物体运动的方向,那这个投影不就像是力在这个方向上真正起作用的部分嘛!(你说是不是很形象呢?)
再来说说向量 a 在平面π上的投影向量。
假设平面π的法向量是 n,那这个投影向量就等于acosθ×(n/n)呀!好比是,把向量 a 往平面π上“投”过去,这个结果向量就是它在平面上的影子呢!(是不是感觉很有意思呀?)假设你有个手电筒照在墙上,那手电筒的光不就类似向量 a,而墙上的影子就是它的投影向量呀!
怎么样,这下对立体几何向量投影公式清楚点了吧!(是不是挺好玩的呀?)。