三种基本逻辑电路运算比较

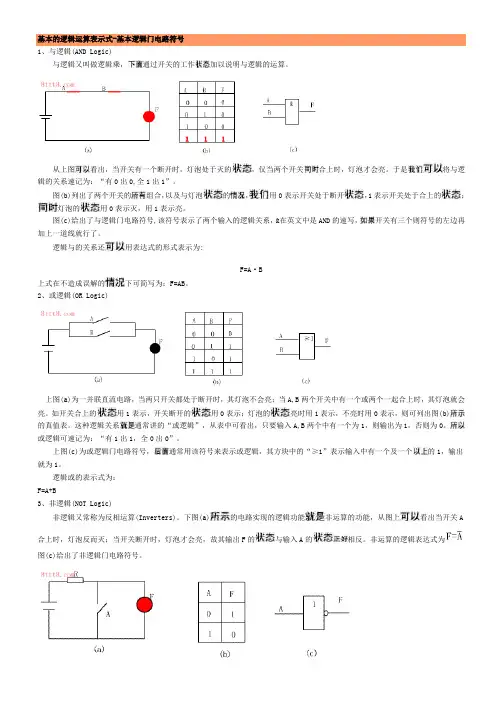
基本的逻辑运算表示式-基本逻辑门电路符号1、与逻辑(AND Logic)与逻辑又叫做逻辑乘，通过开关的工作加以说明与逻辑的运算。

从上图看出，当开关有一个断开时，灯泡处于灭的，仅当两个开关合上时，灯泡才会亮。

于是将与逻辑的关系速记为：“有0出0,全1出1”。

图(b)列出了两个开关的组合，以及与灯泡的，用0表示开关处于断开，1表示开关处于合上的；灯泡的用0表示灭，用1表示亮。

图(c)给出了与逻辑门电路符号,该符号表示了两个输入的逻辑关系，&在英文中是AND的速写，开关有三个则符号的左边再加上一道线就行了。

逻辑与的关系还用表达式的形式表示为:F=A·B上式在不造成误解的下可简写为：F=AB。

2、或逻辑(OR Logic)上图(a)为一并联直流电路，当两只开关都处于断开时，其灯泡不会亮；当A,B两个开关中有一个或两个一起合上时，其灯泡就会亮。

如开关合上的用1表示，开关断开的用0表示；灯泡的亮时用1表示，不亮时用0表示，则可列出图(b)的真值表。

这种逻辑关系通常讲的“或逻辑”，从表中可看出，只要输入A,B两个中有一个为1，则输出为1，否则为0。

或逻辑可速记为：“有1出1，全0出0”。

上图(c)为或逻辑门电路符号，通常用该符号来表示或逻辑，其方块中的“≥1”表示输入中有一个及一个的1，输出就为1。

逻辑或的表示式为：F=A+B3、非逻辑(NOT Logic)非逻辑又常称为反相运算(Inverters)。

下图(a)的电路实现的逻辑功能非运算的功能，从图上看出当开关A 合上时，灯泡反而灭；当开关断开时，灯泡才会亮，故其输出F的与输入A的相反。

非运算的逻辑表达式为图(c)给出了非逻辑门电路符号。

复合逻辑运算在数字系统中，除了与运算、或运算、非运算之外，使用的逻辑运算还有是通过这三种运算派生出来的运算，这种运算通常称为复合运算，的复合运算有：与非、或非、与或非、同或及异或等。

4、与非逻辑(NAND Logic)与非逻辑是由与、非逻辑复合而成的。

第二章逻辑代数与逻辑门电路基本要求：理解“与”逻辑及“与”门、“或”逻辑及“或”门、“非”逻辑及“非”门；理解正、负逻辑的概念，掌握逻辑代数的基本定律、基本规则和常用公式；理解复合逻辑的概念；了解集成门电路的分类；理解TTL、MOS门电路；理解逻辑函数的表示方法；掌握逻辑函数的代数化简法和卡诺图化简法。

本章主要内容：介绍逻辑代数、集成逻辑门电路和逻辑函数化简。

逻辑代数是数字电路的理论基础，是组合逻辑和时序逻辑电路分析、设计中要用到的基本工具；集成逻辑门电路是组成数字逻辑电路的基本单元电路；逻辑函数化简是逻辑电路分析的基础。

本章重点：基本逻辑门电路和功能逻辑代数的基本定律及常用公式逻辑函数的代数化简法本章难点：基本定律、公式及化简法的正确与准确一、逻辑变量与逻辑函数：在逻辑代数中的变量称逻辑变量，用字母Ａ、Ｂ、Ｃ……来表示。

逻辑变量只能有两种取值：真和假。

常把真记作“1”，假记作“0”。

这里的“1”和“0”并不表示数量的大小，而是表示完全对立的两种状态。

在逻辑问题的研究中，涉及到问题产生的条件和结果。

表示条件的逻辑变量称输入变量，表示结果的逻辑变量称输出变量。

将输入变量和输出变量通过逻辑运算符连接起来的式子称逻辑函数，常用Ｆ、Ｌ表示。

基本的逻辑运算有“与”运算、“或”运算、“非”运算。

二、逻辑运算：逻辑运算的值要通过对逻辑变量进行逻辑运算来确定。

1.与运算及与门逻辑运算Ｆ与逻辑变量Ａ、Ｂ的逻辑与运算表达式是：Ｆ＝Ａ·Ｂ, 式中“·”为与运算符。

在逻辑电路中，把能实现与运算的基本单元叫与门，它是逻辑电路中最基本的一种门电路。

二极管构成的与门电路及逻辑符号如下：2.或运算及或门逻辑函数Ｆ与逻辑变量Ａ、Ｂ的逻辑运算表达式是：Ｆ＝Ａ＋Ｂ，式中“＋”为或运算符。

在逻辑电路中，把能实现或运算的基本单元叫或门。

二极管构成的或门电路及逻辑符号如下：3.非逻辑及非门对逻辑变量Ａ进行逻辑非运算的表达式是：Ｆ＝，这里的“－”是非运算符。

三种基本逻辑门电路三种基本的门：全部其它组合规律功能都可由这三种门单之产生。

规律门表示法符号希尔符号NOT （非）ā 或/A — 或/ （非、负）AND （与）A * B * 与（积）OR （或）A+B + （和）二规律门等效于AND 和NOT : NAND 与非门OR 和NT : NOR 或非任何规律功能都可以表示为“ 与非门” 或者“ 或非门” 的功能。

三种基本规律门的真值表运算符的优先级正常的运算次序是：NOT ，AND ，OR, 括号中的内容总是比表达式的其它部分先进行运算。

例：交换律、结合律和安排律AND 功能和OR 功能可以交换和结合。

操作数可以任何次序消失，而不会影响功能的运算结果：1. 交换律2. 结合律3. 安排律1. A*(B+C) = (A*B)+(A*C) ：象标准的代数规章（乘对加）2. A+(B*C) = (A+B)*(A+C) ：真值表或规律变换证明( 加对乘)４.对偶性对偶性原理：– 假如用*替换+，+替换*，1替换0，0替换1，则替换后的表达式与原等式等同。

– 因此只要证明第一条安排律是正确的，通过对偶性就能证明其次条安排律的正确性。

５. 规律运算的法则四条基本公理– 公理1 ：a. X+0=X b. X*0=0– 公理2 ：a. X+/X=1 b. X*/X=0– 公理3 ：a. X+Y=Y+X b. X*Y=Y*X– 公理4 ：a. X*(Y+Z)=(X*Y)+(X*Z) b. X+(Y*Z)=(X+Y) *(X+Z)九条基本交理– 定理1 ：a. X+X=X b. X*X=X– 定理2 ：a. X+1=1 b. X*0=0– 定理3 ：/(/X)=X ( 不包括具有对偶的元素+ 、* 、1 或0) – 定理4 ：a. X+(Y+Z)=(X+Y)+Z l b. X*(Y*Z)=(X*Y) *Z– 定理5 ：a. /(X+Y)=/X*/Y b. /(X*Y)=/X+/Y– 定理6 ：a. X+(X*Y)=X b. X*(X+Y)=X– 定理7 ：a. (X+Y)+(X*/Y)=X b. (X+Y) *(X+/Y)=X– 定理8 ：a. X+(/X*Y)=X+Y b. X*(/X+Y)=X*Y– 定理9 ： a. (X*Y)+(/X*Z)+(Y*Z)=(X*Y)+(/X*Z) b. (X+Y) *(/X+Z)*(Y*Z)=(X+Y)*(/X+Z)除定理3 ，每个定理或公理都有二种形式，属对偶性原理的关系。

数字电路是一种用来处理数字信号的电路，它由逻辑门组成，可以实现各种逻辑运算。

在数字电路中，最基本的三种逻辑运算分别是与运算、或运算和非运算。

本文将对这三种逻辑运算进行详细介绍，以帮助读者更好地理解数字电路的基本原理和运作方式。

1. 与运算与运算是指在两个信号同时为高电平时，输出为高电平；否则输出为低电平。

在数字电路中，与运算通常由与门来实现。

与门有两个输入端和一个输出端，只有在两个输入端同时为高电平时，输出端才会输出高电平。

与门的逻辑符号通常表示为“∧”。

2. 或运算或运算是指在两个信号中至少有一个为高电平时，输出为高电平；只有在两个输入端同时为低电平时，输出端才会输出低电平。

在数字电路中，或运算通常由或门来实现。

或门同样有两个输入端和一个输出端，只要两个输入端中至少有一个为高电平，输出端就会输出高电平。

或门的逻辑符号通常表示为“∨”。

3. 非运算非运算是指将输入信号取反，即如果输入信号为低电平，则输出为高电平；如果输入信号为高电平，则输出为低电平。

在数字电路中，非运算通常由非门来实现。

非门只有一个输入端和一个输出端，其输出信号与输入信号相反。

非门的逻辑符号通常表示为“¬”。

通过这三种最基本的逻辑运算，数字电路可以实现各种复杂的逻辑功能。

通过组合多个与门、或门和非门，可以构建出加法器、减法器、乘法器、除法器等各种算术逻辑单元，从而实现数字信号的加减乘除运算。

这三种逻辑运算的组合还可以实现逻辑判断、比较、选择等功能，为数字系统的设计和实现提供了基础。

数字电路中的与运算、或运算和非运算是最基本的逻辑运算，它们是数字电路的基石。

通过这三种逻辑运算，我们可以实现各种复杂的数字逻辑功能，从而构建出功能强大的数字系统。

希望本文对读者理解数字电路和逻辑运算有所帮助，谢谢阅读！上文中我们已经介绍了数字电路中最基本的三种逻辑运算，接下来我们将继续探讨这些逻辑运算在数字电路中的应用以及它们的扩展。

4. 异或运算异或运算是指在两个信号不输出为高电平；两个输入端相同时输出为低电平。

基本逻辑关系通常，把反映“条件”和“结果”之间的关系称为逻辑关系.如果以电路的输入信号反映“条件”，以输出信号反映“结果",此时电路输入、输出之间也就存在确定的逻辑关系。

数字电路就是实现特定逻辑关系的电路，因此，又称为逻辑电路。

逻辑电路的基本单元是逻辑门,它们反映了基本的逻辑关系。

基本逻辑关系和逻辑门基本逻辑关系和逻辑门逻辑电路中用到的基本逻辑关系有与逻辑、或逻辑和非逻辑，相应的逻辑门为与门、或门及非门.一、与逻辑及与门与逻辑指的是:只有当决定某一事件的全部条件都具备之后，该事件才发生，否则就不发生的一种因果关系。

如图2。

1.1所示电路，只有当开关A 与B 全部闭合时，灯泡Y 才亮;若开关A 或B 其中有一个不闭合,灯泡Ｙ就不亮。

这种因果关系就是与逻辑关系，可表示为Y ＝A •B ，读作“A 与B”。

在逻辑运算中，与逻辑称为逻辑乘。

与门是指能够实现与逻辑关系的门电路。

与门具有两个或多个输入端，一个输出端。

其逻辑符号如图2。

1.2所示，为简便计，输入端只用A 和B 两个变量来表示。

与门的输出和输入之间的逻辑关系用逻辑表达式表示为： Y ＝A •B ＝AB两输入端与门的真值表如表2.1.1所示.波形图如图2。

1.3所示。

A B Y0 0 0 0 1 0 1 0 0 1 11（a)常用符号表2.1.1 与门真值表 图2.1.1 与逻辑举例（b ）国标符号图2.1.2 与逻辑符号由此可见,与门的逻辑功能是，输入全部为高电平时，输出才是高电平，否则为低电平。

二、或逻辑及或门或逻辑指的是：在决定某事件的诸条件中，只要有一个或一个以上的条件具备,该事件就会发生；当所有条件都不具备时,该事件才不发生的一种因果关系。

如图2.1。

4所示电路，只要开关A 或B 其中任一个闭合，灯泡Y 就亮；A 、B 都不闭合，灯泡Y 才不亮。

这种因果关系就是或逻辑关系。

可表示为：Y ＝A ＋B读作“A 或B”.在逻辑运算中或逻辑称为逻辑加。