精选-28 2.2.1综合法和分析法-word文档

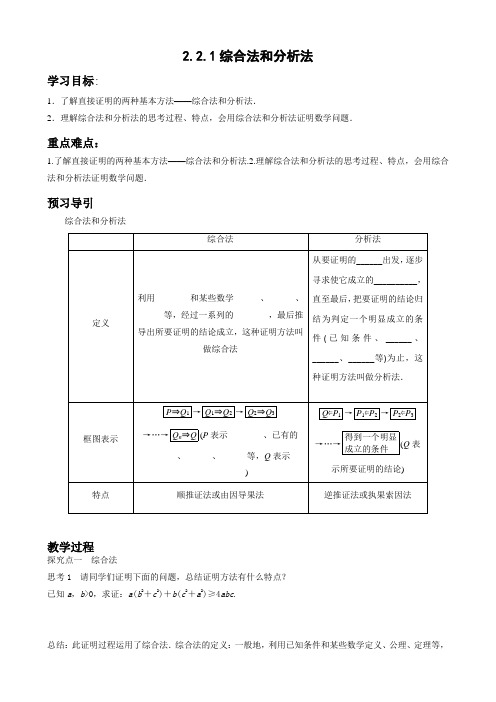
2.2.1综合法和分析法学习目标:1．了解直接证明的两种基本方法——综合法和分析法．2．理解综合法和分析法的思考过程、特点，会用综合法和分析法证明数学问题．重点难点：1.了解直接证明的两种基本方法——综合法和分析法.2.理解综合法和分析法的思考过程、特点，会用综合法和分析法证明数学问题．预习导引综合法和分析法教学过程探究点一综合法思考1 请同学们证明下面的问题，总结证明方法有什么特点？已知a，b>0，求证：a(b2＋c2)＋b(c2＋a2)≥4abc.总结：此证明过程运用了综合法．综合法的定义：一般地，利用已知条件和某些数学定义、公理、定理等，经过一系列的推理论证，最后推导出所要证明的结论成立，这种证明方法叫做综合法． 思考2 综合法又叫由因导果法，其推理过程是合情推理还是演绎推理？例1 在△ABC 中，三个内角A ，B ，C 的对边分别为a ，b ，c ，且A ，B ，C 成等差数列，a ，b ，c 成等比数列，求证：△ABC 为等边三角形．跟踪训练1 在△ABC 中，AC AB ＝cos Bcos C，证明：B ＝C .探究点二 分析法思考1 回顾一下：基本不等式a ＋b2≥ab (a >0，b >0)是怎样证明的？思考2 证明过程有何特点？小结 分析法定义：一般地，从要证明的结论出发，逐步寻求使它成立的充分条件，直至最后，把要证明的结论归结为判定一个明显成立的条件(已知条件、定理、定义、公理)为止，这种证明方法叫做分析法． 思考3 综合法和分析法的区别是什么？例2 求证：3＋7<2 5.跟踪训练2 求证：a －a －1<a －2－a －3(a ≥3)．探究点三 综合法和分析法的综合应用思考 在实际证题中，怎样选用综合法或分析法？例3 已知α，β≠k π＋π2(k ∈Z )，且sin θ＋cos θ＝2sin α， ① sin θcos θ＝sin 2β. ②求证：1－tan 2α1＋tan 2α＝1－tan 2β＋tan 2β.反思与感悟 用P 表示已知条件、定义、定理、公理等，用Q 表示要证明的结论，则综合法和分析法的综合应用可用框图表示为：跟踪训练3 若tan(α＋β)＝2tan α，求证：3sin β＝sin(2α＋β)．课后总结1．综合法证题是从条件出发，由因导果；分析法是从结论出发，执果索因． 2．分析法证题时，一定要恰当地运用“要证”、“只需证”、“即证”等词语． 3．在解题时，往往把综合法和分析法结合起来使用.课后检测1．已知y >x >0，且x ＋y ＝1，那么( ) A ．x <x ＋y2<y <2xy B ．2xy <x <x ＋y2<y C ．x <x ＋y 2<2xy <yD ．x <2xy <x ＋y2<y2．欲证2－3<6－7成立，只需证( ) A ．(2－3)2<(6－7)2B ．(2－6)2<(3－7)2C ．(2＋7)2<(3＋6)2D ．(2－3－6)2<(－7)23．求证：1log 519＋2log 319＋3log 219<2.4．已知1－tan α2＋tan α＝1，求证：cos α－sin α＝3(cos α＋sin α)．课后作业一、选择题1．分析法是从要证明的结论出发，逐步寻求使结论成立的( ) A ．充分条件 B ．必要条件 C ．充要条件 D ．等价条件2．已知a ，b ，c 为三角形的三边且S ＝a 2＋b 2＋c 2，P ＝ab ＋bc ＋ca ，则( ) A ．S ≥2P B ．P <S <2P C ．S >P D ．P ≤S <2P3．已知函数f (x )在(－∞，＋∞)上是减函数，则方程f (x )＝0的根的情况为( ) A ．至多有一个实根 B ．至少有一个实根 C ．有且只有一个实根 D ．无实根4．若a ＝ln 22，b ＝ln 33，c ＝ln 55，则( )A ．a <b <cB ．c <b <aC ．c <a <bD ．b <a <c5．若f (n )＝n 2＋1－n ，g (n )＝n －n 2－1，φ(n )＝12n ，n ∈N *，则f (n )、g (n )、φ(n )的大小关系为( )A ．f (n )<g (n )<φ(n )B ．f (n )<φ(n )<g (n )C ．g (n )<φ(n )<f (n )D ．g (n )<f (n )<φ(n )6．在不等边三角形中，a 为最大边，要想得到∠A 为钝角的结论，三边a ，b ，c 应满足什么条件( ) A ．a 2<b 2＋c 2B ．a 2＝b 2＋c 2C ．a 2>b 2＋c 2D ．a 2≤b 2＋c 27．如果a a ＋b b >a b ＋b a ，则正数a ，b 应满足的条件是________．8．设a 、b 、u 都是正实数且a 、b 满足1a ＋9b＝1，则使得a ＋b ≥u 恒成立的u 的取值范围是____________．9．设a ＝3＋22，b ＝2＋7，则a 、b 的大小关系为________________________________________________________________________． 三、解答题10．设a ，b >0，且a ≠b ，求证：a 3＋b 3>a 2b ＋ab 2.11．已知△ABC 的三个内角A ，B ，C 成等差数列，对应的三边为a ，b ，c ， 求证：1a ＋b ＋1b ＋c ＝3a ＋b ＋c.能力提升 12.如图所示，在直四棱柱A 1B 1C 1D 1—ABCD 中，当底面四边形ABCD 满足条件________时，有A 1C ⊥B 1D 1.(注：填上你认为正确的一种条件即可，不必考虑所有可能的情形)13．已知函数f (x )＝1＋x 2，若a ≠b ，求证：|f (a )－f (b )|<|a －b |.。

§2.2 直接证明与间接证明 2．2.1 综合法和分析法(一)课时目标 1.了解直接证明的两种基本方法——分析法和综合法.2.理解分析法和综合法的思考过程、特点，会用分析法和综合法证明数学问题．综合法分析法定义利用__________和某些数学______、______、______等，经过一系列的____________，最后推导出所要证明的结论成立，这种证明方法叫做综合法从要证明的______，逐步寻求使它成立的____________，直至最后，把要证明的结论归结为判定一个明显成立的条件(已知条件、______、______、______等)，这种证明方法叫做分析法框图表示 P ⇒Q 1→Q 1⇒Q 2→Q 2⇒Q 3→…→Q n ⇒Q (P 表示________、已 有的______、______、 ______等，Q 表示 ________________) Q ⇐P 1→P 1⇐P 2→ P 2⇐P 3→…→ 得到一个明显成立的条件特点顺推证法或由因导果法逆推证法或执果索因法一、选择题1．已知x ≥52，则f (x )＝x 2－4x ＋52x －4有( )A ．最大值54B ．最小值54C ．最大值1D ．最小值12．命题“对于任意角θ，cos 4θ－sin 4θ＝cos 2θ”的证明：“cos 4θ－sin 4θ＝(cos 2θ－sin 2θ)(cos 2θ＋sin 2θ)＝cos 2θ－sin 2θ＝cos 2θ”过程应用了( )A ．分析法B ．综合法C ．综合法、分析法综合使用D ．间接证法3．如果x >0，y >0，x ＋y ＋xy ＝2，则x ＋y 的最小值是( )A ．32B ．23－2C ．1＋ 3D ．2－ 34．要证明a ＋a ＋7<a ＋3＋a ＋4 (a ≥0)可选择的方法有多种，其中最合理的是( )A ．综合法B ．类比法C ．分析法D ．归纳法5．已知实数a ，b ，c 满足a ＋b ＋c ＝0，abc >0，则1a ＋1b ＋1c的值( )A ．一定是正数B ．一定是负数C ．可能是零D ．正、负不能确定二、填空题6．设a ＝3＋22，b ＝2＋7，则a 、b 的大小关系为________．7．已知a 、b 、u ∈R *，且1a ＋9b＝1，则使得a ＋b ≥u 恒成立的u 的取值范围是__________．8．设a ＝2，b ＝7－3，c ＝6－2，则a ，b ，c 的大小关系为__________．三、解答题9．已知a >0，b >0，求证：b 2a ＋a 2b≥a ＋b .10．已知a ，b ，c ，d ∈R ，求证：ac ＋bd ≤(a 2＋b 2)(c 2＋d 2).能力提升11．a >b >c ，n ∈N *，且1a －b ＋1b －c ≥na －c恒成立，则n 的最大值为________．12．已知a >0，b >0，用两种方法证明：a b ＋ba≥a ＋b .1．运用综合法解题时，要保证前提条件正确，推理要合乎逻辑规律，只有这样才能保证结论的正确性．2．在分析法证明中，从结论出发的每一个步骤所得到的判断都是使结论成立的充分条件．最后一步归结到已被证明了的事实．因此，从最后一步可以倒推回去，直到结论，但这个倒推过程可以省略．§2.2 直接证明与间接证明 2．2.1 综合法和分析法(一)答案综合法 分析法定利用已知条件和某些数学定义、定理、从要证明的结论，逐步寻求使它成立的充分条1．D [f (x )＝x －22＋12(x －2)∵x －2≥12，∴f (x )≥2·x －22×12(x －2)＝1.当x ＝3时，f (x )min ＝1.]2．B [从证明的过程来看是从已知条件入手经过推导得到结论，符合综合法．] 3．B [由x >0，y >0，x ＋y ＋xy ＝2，则2－(x ＋y )＝xy ≤⎝⎛⎭⎫x ＋y 22， ∴(x ＋y )2＋4(x ＋y )－8≥0，∴x ＋y ≥23－2或x ＋y ≤－2－2 3.∵x >0，y >0，∴x ＋y 的最小值为23－2.] 4．C [要证a ＋a ＋7<a ＋3＋a ＋4， 只要证a ＋a ＋7＋2a (a ＋7) <a ＋3＋a ＋4＋2(a ＋3)(a ＋4)， 只要证a 2＋7a <a 2＋7a ＋12， 只要证a 2＋7a <a 2＋7a ＋12， 只要证0<12.由此可知，最合理的是分析法．]5．B [∵a ＋b ＋c ＝0，∴(a ＋b ＋c )2＝0， ∴a 2＋b 2＋c 2＋2(ab ＋bc ＋ac )＝0，∴ab ＋bc ＋ac ＝－12(a 2＋b 2＋c 2)<0.又abc >0，∴1a ＋1b ＋1c ＝ab ＋bc ＋acabc<0.]6．a <b解析 a ＝3＋22，b ＝2＋7两式的两边分别平方，可得a 2＝11＋46，b 2＝11＋47，明显6<7，故a <b .7．(－∞，16]解析 ∵a ＋b ＝(a ＋b )⎝⎛⎭⎫1a ＋9b＝10＋b a ＋9a b ≥10＋2b a ×9a b ＝16，当且仅当b a ＝9ab即3a ＝b 时取等号，若a ＋b ≥u 恒成立，则u ≤16. 8．a >c >b解析 b ＝47＋3，c ＝46＋2，显然b <c . 而a 2＝2，c 2＝8－212＝8－48 <8－36＝2＝a 2， ∴a >c .9．证明 ∵b 2a ＋a 2b ＝a 3＋b3ab＝(a ＋b )(a 2－ab ＋b 2)ab，又∵a >0，b >0，∴a 2－ab ＋b 2－ab ＝(a －b )2≥0，∴a 2－ab ＋b 2≥ab ，∴a 2－ab ＋b 2ab≥1，∴(a ＋b )·a 2－ab ＋b 2ab≥a ＋b .∴b 2a ＋a 2b≥a ＋b . 10．证明 ①当ac ＋bd ≤0时，显然成立． ②当ac ＋bd >0时，欲证原不等式成立， 只需证(ac ＋bd )2≤(a 2＋b 2)(c 2＋d 2)．即证a 2c 2＋2abcd ＋b 2d 2≤a 2c 2＋a 2d 2＋b 2c 2＋b 2d 2. 即证2abcd ≤b 2c 2＋a 2d 2. 即证0≤(bc －ad )2.因为a ，b ，c ，d ∈R ，所以上式恒成立． 故原不等式成立，综合①、②知，命题得证． 11．4解析 ∵a >b >c ，∴a －b >0，b －c >0，a －c >0.若1a －b ＋1b －c ≥n a －c 恒成立， 即a －c a －b ＋a －c b －c≥n 恒成立． a －c a －b ＋a －c b －c ＝a －b ＋b －c a －b ＋a －b ＋b －cb －c ＝2＋b －c a －b ＋a －b b －c ≥2＋2b －c a －b ·a －b b －c ＝4.∴当且仅当a －b ＝b －c 时取等号． ∴n 的最大值为4.12．证明 方法一 (综合法)： 因为a >0，b >0，所以a b ＋ba －a －b＝⎝⎛⎭⎫a b －b ＋⎝⎛⎭⎫ba －a ＝a －b b ＋b －aa＝(a －b )⎝⎛⎭⎫1b －1a＝(a －b )2(a ＋b )ab ≥0，所以a b ＋ba≥a ＋b .方法二(分析法)：要证ab＋ba≥a＋b，只需证a a＋b b≥a b＋b a，即证(a－b)(a－b)≥0，因为a>0，b>0，a－b与a－b同号，所以(a－b)(a－b)≥0成立，所以ab＋ba≥a＋b成立．。

221综合法和分析法班级：姓名：小组:学习目标1. 了解直接证明的两种基本方法：综合法和分析法；2. 掌握综合法分析法证明数学问题；学习重点难点重点：综合法和分析法的应用；难点：综合题型的解决。

学法指导本节课通过例题让学生体会综合法和分析法的思想，通过练习掌握综合法和分析法的应用。

课刖预习1. 综合法的定义：利用和某些数学、、等，经过一系列的，最后推导出所要证明的成立，这种证明方法叫做综合法。

2. 分析法的定义：从出发，逐步寻求使它成立的，直至最后，把要证明的结论归结为判定一个明显成立的条件（、、、等）为止，这种证明方法叫做分析法。

预习评价1. 已知a,b,c€ R,那么下列命题正确的是（）A.若a Ab,则ac2 >bc2B. 若—>—,则a > bc c2 211C 北 3 3 □丽［1 1 若a >b ,且abAO,则一v —C.右a >b ,且ab £0,则一a—D. a ba b2. 设a = >/2,b = -x/3,c = Q6 -72,则a, b, c的大小关系为。

课堂学习研讨、合作交流（备注：重、难点的探究问题）一、综合合法的应用1 1例1. 已知a,b是正数，且a+b = 1，求证：丄十丄＞4a b 二、分析法的应用例2.用分析法证明不等式戸_1＞的7丐小结：分析法证明不等式的思路：从要证明的不等式出发，逐步寻求使它成立的充分条件，最后得到的充分条件是已知（或已证）的不等式.当堂检测（备注：本节课重、难点知识的检测）1. 要证明U a + Ja + 7 “a+3 + Ja+4 （a^O）可选择的方法有多种，其中最合理的是（）A.综合法B. 类比法C.分析法D. 归纳法2. 下面命题可作为实数a,b,c不全为0的条件的是（）A. a,b,c均不为0B. a,b,c至少有一个为0C. a,b,c至多有一个为0D. a,b,c至少有一个不为03. 已知a,b,c^ R,且不全相等，求证：a2+b2+ c2a ab+bc+ca。