- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
于是,所求概率为:
P( X 2)C (0.05) (0.95) 0.007125
2 3 2
请注意:
1、若将本例中的“有放回”改为”无放回”, 那么 各次试验条件就不同了, 此试验就不是伯努利试验 . 此时, 只能用古典概型求解.
P( X 2)
C C C
1 95
2 5
3 100
0.00618
这种对应关系在数学上理解为定义了一种实值 单值函数.定义域为样本空间S,取值为实数.
e.
s
这即为所谓的随机变量
X(e)
R
定义 设随机试验的样本空间为S={e}. X= X(e)是 定义在样本空间S上的实值单值函数.称X= X(e)为 随机变量. 简记为 r.v. 说明 (1)它是一个变量, 它的取值随试验结果而改变 (2)由于试验结果的出现具有一定的概率,故 随机变量取每个值和每个确定范围内的值也有一 定的概率. (3)随机变量通常用大写字母X,Y,Z,W,N 等表 示,而表示随机变量所取的值时,一般采用小写 字母 x, y, z, w, n等.
解:按第一种方法。 以 X 记 “ 第 一 人 维 护 的 20台 中 同 一 时 刻 发 生 故 障 的 台 数 ” 。 以 Ai i 1, 2, 3, 4 表 示 事 件 “ 第 i 人 维 护 的 2 0台 中 发 生 故 障 不 能 及 时 维 修 ” , 则 知 80台 中 发 生 故 障 不 能 及 时 维 修 的 概 率 为 :
k k nk
, 0, , n k 1,
P 易证:(1) ( X k ) 0
(2) P ( X k ) 1
k 0
n
称 r.v X 服从参数为n和p的二项分布,记作 X~b(n,p) 显然,当 n=1 时 X ~ B 1, p 此时有 PX k p k 1 p 1 k , k 0,1 0 p 1
2
1/6
求 P(0<X≤2) 解
P(0<X≤2)=P(X=1)+P(X=2)
=1/2+1/6=2/3
即分布律确定概率
(几何分布) 例3(课本例1) 一汽车在开往目的地的路上需要通过四组信 号灯,每个信号灯以1/2的概率允许或禁止汽车通过. 以X表示该 汽车首次停下时它已通过的信号灯个数,求X的分布律.(设各 组信号灯工作是相互独立)
k 3 k 3 k
, k 0,1,2,3
把观察一个灯泡的使用 时数看作一次试验, “使用到1000小时已坏” 视为事件A .每次试验, A 出现的概率为0.8
P{X 1} =P{X=0}+P{X=1} =(0.2)3+3(0.8)(0.2)2
=0.104
例5:(课本45页例题4) 设有80台同类型设备,各台工作是相互独 立的,发生故障的概率都是0.01,且一台设备 的故障能有一个人处理。 考虑两种配备维修工人的方法, 其一是由4个人维护,每人负责20台; 其二是由3个人共同维护80台。 试比较这两种方法在设备发生故障时不能及时 维修的概率的大小。
P( X k) a , k!
k =0,1,2, …,
0
试确定常数a . 解: 依据分布律的性质
P(X =k)≥0,
P( X k) 1
k
即
a≥0 ,
a
k 0
k
ae 1
e
k 0
k
k!
k!
从中解得
ae
例2
设X的分布律为
X
P
-1
1/3Biblioteka 11/2主要内容
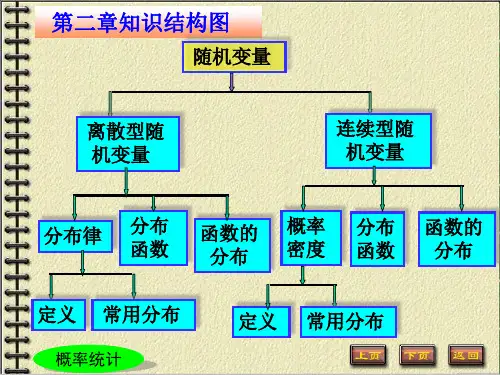
第一节
第二节 第三节 第四节 第五节 小结
随机变量
离散型随机变量及其分布律 随机变量的分布函数 连续型随机变量及其概率密度 随机变量的函数的分布
第一节
随机变量的概念
随机变量概念的引入
引入随机变量的意义
随机变量的分类
一、随机变量概念的引入
(1)、有些试验结果本身与数值有关(本身就是一 个数). 例如,掷一颗骰子面上出现的点数; 每天进入四号教学楼的人数; 9月份南宁的最高温度;
即(0-1)分布是二项分布的一个特例.
二项分布分布律的推导
设A在n重贝努利试验中发生X次,则
P ( X k ) C n p (1 p )
k k nk
, 0, , n k 1,
并称X服从参数为p的二项分布,记
注 :1 ( p q )
n
X b ( n, p )
X和Y都是离散型随机变量
二、离散型随机变量的分布律
定义2 :设 xk (k=1,2, …) 是离散型随机变量 X 所 取的一切可能值,称
P{ X xk } pk , k 1, 2,
为离散型随机变量 X 的分布律. 其中
pk (k=1,2, …) 满足:
(1) pk 0, (2) pk 1
2、如果产品总数很大,且抽查的产品个 数相对于产品总数来说很小,则可以当作 有放回抽样处理,如课本43页例题2
伯努利试验对试验结果没有等可能的要求, 但有下述要求: (1)每次试验条件相同; (2)每次试验只考虑两个互逆结果 A 或 A , 且 P(A)=p , ( A) 1 p ; P (3)各次试验相互独立. 可以简单地说,
1 1
3 1
P ( X 2) P ( A1 A 2 A3 A1 A 2 A3 A1 A 2 A3 ) C 3 p (1 p )
2 2
3 2
P ( X 3) P ( A1 A 2 A3 ) p
3
一般地:
P ( X k ) C n p (1 p )
k k
n k
, 0, , n k 1,
例4 已知100个产品中有5个次品,现从中有放回 地取3次,每次任取1个,求在所取的3个中恰有2 个次品的概率.
解: 因为这是有放回地取3次,因此这3 次试验 的条件完全相同且独立,它是贝努里试验. 依题意,每次试验取到次品的概率为0.05. 设X为所取的3个中的次品数, 则 X ~ b(3,0.05),
例如:
抽验产品:“是正品”,“是次品”
将伯努利试验E独立地重复地进行n次 ,则称这 一串重复的独立试验为n重伯努利试验 . “重复”是指这 n 次试验中P(A)= p 保持不变.
“独立”是指各 次试验的结果互不影响 .
用X表示n重伯努利试验中事件A发生 的次数,则X分布律为
P ( X k ) C n p (1 p )
C
k 0
n
k n
p q
k
nk
其中q 1 p
推导:设Ai={ 第i次A发生 },先设n=3
P ( X 0) P ( A1 A 2 A3 ) (1 p )
3
P ( X 1) P ( A1 A 2 A3 A1 A 2 A3 A1 A 2 A3 ) C 3 p (1 p )
P A1 A2 A3 A4 P A1 P X 2
而 X b 20, 0.01 , 故 有 :
P X 2 1
1
P X k 1
k 0
1
C 2 0 0 .0 1
k
k
0 .9 9
20 k
0 .0 1 6 9
k 0
即 有 : P A1 A2 A3 A4 0.0169
按 第 二 种 方 法 。 以 Y 记 8 0台 中 同 一 时 刻 发 生 故 障 的 台 数 , 此 时 , Y b 8 0, 0 .0 1 , 故 8 0台 中 发 生 故 障 而 不 能 及 时 维 修 的 概 率 为 :
(2)、在有些试验中,试验结果看来与数值无关, 但我们可以引进一个变量来表示它的各种结果.也 就是说,把试验结果数值化.
例如: 掷硬币试验,考察其正面和反面朝上的情况
可规定: 用 1表示 “正面朝上” 上”
用 0 示“反面朝
结论:不管试验结果是否与数值有关,我们都可以通过
引入某个变量,使试验结果与数建立了对应关系
2
P { X 3} (1 p ) p
3
P { X 4 } (1 p )
4
故X 的分布律为:
P{X= k} = (1- p)kp,k = 0,1,2,3 P{X= 4} = (1-p)4 用表格表示为: X 0 1 2 3 4
pk
p (1-p) p (1-p)2p (1-p)3p (1-p)4
二项分布描述的是n重伯努利试验中事件 A 出现 的次数 X 的分布律 .
例5某类灯泡使用时数在1000小时以上 的概率是0.2,求三个灯泡在使用1000 小时以后最多只有一个坏了的概率.
解: 设X为三个灯泡在使用1000小时已坏的灯泡数 .
X ~ b (3, 0.8),
P( X k )C (0.8) (0.2)
事件A={收到不少于1次呼叫}
{ X 1}
B={没有收到呼叫} {X= 0} 而有 P{A}=P{X>=1} P{B}=P{X=0}
三、随机变量的分类
我们将研究两类随机变量:
随 机 变 量
离散型随机变量
连续型随机变量
这两种类型的随机变量因为都是随机变量, 自然有很多相同或相似之处;但因其取值方式不 同,又有其各自的特点.
以 p = 1/2 代入得:
X 0 1 0.5 0.25 2 3 4
pk
0.125
0.0625
0.0625
三、几种常见分布
1、(0-1)分布:(也称两点分布)