下载文档原格式
4种混沌映射的特点
混沌映射是一种重要的非线性动力学系统，具有复杂的动力学特性，已经被广泛应用于许多领域。
本文介绍了四种常见的混沌映射及其特点。
1. Logistic映射
Logistic映射是一种广泛应用于混沌理论研究中的典型非线性动力学系统。
它的特点是简单易行，具有双稳态和混沌行为，是研究混沌现象的经典示例。
2. Henon映射
Henon映射是一种双参数混沌映射，它的特点是具有分形结构、非周期性、高度敏感依赖于初值和参数，并且在参数空间中形成了复杂的混沌吸引子。
3. Lorenz映射
Lorenz映射是一种具有吸引子的三维非线性动力学系统，它的特点是具有强的混沌行为和灵敏的初始条件依赖性，常被用于模拟大气和海洋中的流体运动。
4. Ikeda映射
Ikeda映射是一种典型的非线性动力学系统，它的特点是具有高度敏感的初值和参数、分形结构和复杂的混沌吸引子，常被用于研究光学系统中的非线性动力学现象。
以上是四种典型的混沌映射及其特点。
混沌映射在科学研究、信息加密、密码学、图像处理等领域有着广泛的应用价值，未来将会有
更多的研究和应用。
基于Henon 混沌映射的图像加密实验一、实验目的1． 熟悉具有分组密码结构特性的混沌映射；2． 掌握利用二维Henon 混沌映射实现图像像素扩散加密的原理； 3． 培养学生从事高维信号安全保护的动手编程能力。
二、实验原理通过读操作获取图像像素值，然后利用Henon 混沌映射实现像素值扩散操作，其结果通过写操作写入加密后文件。
1、对于长宽相等（M=N ）的图像加密解密原理如下： （1）加密过程 加密函数为：21211(1)mod ()mod n n n n n n x ax by My cx dx N+++⎧=-+⎪⎨=+⎪⎩ （2-1）其中，a=5; b=1;c=1;d=3;(,)n n x y 为原图像像素值的位置，11(,)n n x y ++为改变后的位置。
modM 为对M 取余数。
同理modN 也是。
改变像素值并赋给新的位置11(,)n n x y ++，公式如下：2211(,)[(,)]mod 256n n n n n n data x y A x y x y ++=++ （2-2）（2）解密过程为：有（2-1）得， 2111n nn x ax y l M +=-+- （2-3）2112n n n y x dx l N ++=+- （2-4）由（2-3）得2112n n n x y dx l N ++=-+，等式两边同时对M 取余数，得211()mod n n n x y dx M ++=- （2-5）然后把n x 代入（2-3），整理得2111n n ny x ax l M +=-++，最后把等式两边同时对N 取余数得：21(1)mod n n n y x ax N +=-+（2-5）由式（2-2）可得像素值的恢复：2211(,)[(,)]mod 256n n n n n n A x y data x y x y ++=-- （2-6）2、对于长宽不相等（M ≠N ）的图像加密加密解密原理如下：（1）加密过程加密函数为：11()mod ((1))mod n n n n n n x x y My cx c y N++⎧=+⎪⎨=++⎪⎩ （2-7）其中，c=N/gcd(M,N)；改变像素值并赋给新的位置11(,)n n x y ++，公式如下：2211(,)[(,)]mod 256n n n n n n data x y A x y x y ++=++ （2-8）（2）解密过程为： 由加密函数得：11n n n x x y l M +=+-（2-9） 12(1)n n n y cx c y l N +=++-（2-10）对（2-9）两边同时乘以c,然后（2-10）减去（2-9）整理可得：1112n n n y cx y cl M l N ++-=+- （2-11）（2-11）两边对N 取余整理可得：11()mod n n n y y cx N ++=- （2-12）把y n 代入（2-9），然后两边对M 取余整理可得：1()mod n n n x x y M +=- （2-13）由（2-8）可恢复像素值的大小：2211(,)[(,)]mod 256n n n n n n A x y data x y x y ++=-- （2-14）三、实验步骤1．熟悉图像加密解密原理；2．熟悉Henon 混沌系统；3．采用Matlab 编写图像加解密程序并仿真测试；四、程序代码1、（M=N ） clc; clear;I=imread('C:\Users\Lilong\Desktop\matlab\dianzishiyan\lena.bmp'); figure(1)subplot(2,2,1); imshow(I);title('原始图像');A=double(rgb2gray(I)); %转换成灰度图像subplot(2,2,2);imshow(uint8(A));%显示灰度图像title('灰度图像');[M,N]=size(A);%获取图像的大小data=zeros(M,N);a=5; b=1; c=1; d=3;A1=zeros(M,N);for loop=1:2for x=1:Mfor y=1:Nx1=mod((1-a*x^2+b*y),M);%改变行值if x1==0x1=M;endy1=mod((c*x+d*x1^2),N);%改变列值if y1==0y1=N;enddata(x1,y1)=mod(A(x,y)+x^2+y^2,256);%改变像素数值并赋值给新的位置endendA1=data;endsubplot(2,2,3);imshow(uint8(A1));%显示解密后的图像title('加密后图像');A2=zeros(M,N);A3=zeros(M,N);for loop=1:2for x1=1:Mfor y1=1:Nx2=mod(y1-d*x1^2,M);%解密原来的行值if x2==0x2=M;endy2=mod(x1+a*x2^2-1,N);%解密原来的列值if y2==0y2=N;endA2(x2,y2)=mod(A1(x1,y1)-x2^2-y2^2,256);%恢复像素值endendA3=A2;endsubplot(2,2,4);imshow(uint8(A3));%显示解密后的图像title('解密后图像');2、（M≠N）clc;clear;I=imread('C:\Documents and Settings\Administrator\桌面\lena.bmp'); figure(1)subplot(2,2,1);imshow(I);title('原始图像');I1=I(51:150,31:170,1:3);%裁剪图像A=double(rgb2gray(I1));%转换成灰度图像subplot(2,2,2);imshow(uint8(A));title('灰度图像');[M,N]=size(A);data=zeros(M,N);c=N/gcd(M,N);A1=zeros(M,N);for loop=1:2for x=1:Mfor y=1:Nx1=mod(x+y,M);if x1==0x1=M;endy1=mod(c*x+(1+c)*y,N);if y1==0y1=N;enddata(x1,y1)=mod(A(x,y)+x^2+y^2,256);%改变像素值%data(x1,y1)=A(x,y);endendA1=data;endsubplot(2,2,3);imshow(uint8(A1));title('加密后图像');%加密后的图像A2=zeros(M,N);A3=zeros(M,N);for loop=1:2for x1=1:Mfor y1=1:Ny2=mod(y1-c*x1,N);if y2==0y2=N;endx2=mod(x1-y2,M);if x2==0x2=M;endA2(x2,y2)=mod(A1(x1,y1)-x2^2-y2^2,256);%恢复像素值%A2(x2,y2)=A1(x1,y1);endendA3=A2;Endsubplot(2,2,4);imshow(uint8(A3));title('解密后图像');五、仿真测试运行程序，结果如下图，可以正确解密加密后的图像。
henon映射的迭代轨迹
Henon映射是一种二维动力系统，它是由Michel Henon在1976
年提出的。
这个动力系统在混沌理论中有着重要的应用。
Henon映射可以用以下的式子表示：
x_n+1 = 1 - a * x_n^2 + y_n
y_n+1 = b * x_n
其中a和b是映射的参数，通常取值范围为0到1。
通过对这个式子进行迭代，我们可以得到Henon映射的迭代轨迹。
这个迭代轨迹是由一系列的点组成的，每个点的坐标是(x_n, y_n)。
Henon映射的迭代轨迹具有以下的特点：
1. 对于不同的参数a和b，Henon映射的迭代轨迹可以呈现出不同的形态，包括周期轨道、分岔图、混沌吸引子等。
2. 在Henon映射的迭代过程中，轨迹会不断地变形和扭曲，这
种变形和扭曲的程度取决于参数a和b的取值。
3. Henon映射的迭代轨迹在维度上是二维的，因此可以用二维
图像来展现它的形态。
通过对Henon映射的迭代轨迹进行分析和研究，可以帮助我们更好地理解混沌理论以及动力系统的行为。
- 1 -。
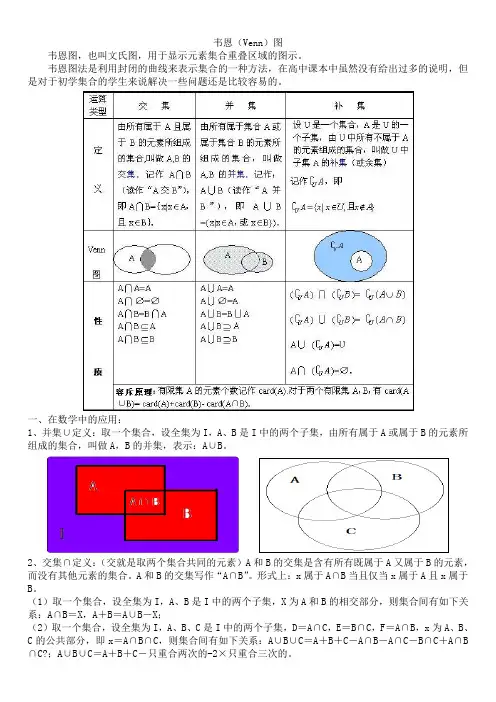
韦恩（Venn）图韦恩图，也叫文氏图，用于显示元素集合重叠区域的图示。
韦恩图法是利用封闭的曲线来表示集合的一种方法，在高中课本中虽然没有给出过多的说明，但是对于初学集合的学生来说解决一些问题还是比较容易的。
一、在数学中的应用：1、并集∪定义：取一个集合，设全集为I，A、B是I中的两个子集，由所有属于A或属于B的元素所组成的集合，叫做A，B的并集，表示：A∪B。
2、交集∩定义：（交就是取两个集合共同的元素）A和B的交集是含有所有既属于A又属于B的元素，而没有其他元素的集合。
A和B的交集写作“A∩B”。
形式上：x属于A∩B当且仅当x属于A且x属于B。
（1）取一个集合，设全集为I，A、B是I中的两个子集，X为A和B的相交部分，则集合间有如下关系：A∩B＝X，A＋B＝A∪B－X；（2）取一个集合，设全集为I，A、B、C是I中的两个子集，D＝A∩C，E＝B∩C，F＝A∩B，x为A、B、C的公共部分，即x＝A∩B∩C，则集合间有如下关系：A∪B∪C＝A＋B＋C－A∩B－A∩C－B∩C＋A∩B ∩C?；A∪B∪C＝A＋B＋C－只重合两次的-2×只重合三次的。
二、运用韦恩（Venn ）图解题“三层次由于图形简明、直观，因此很多数学问题解题往往借助于图形来分析，下面例析运用集合中“韦恩图”解题的三层次：识图——用图——构图。
1、识图是指给出韦恩图形式，用集合的交、并及补等集合的运算表示。
例1：如图，I 是全集，M 、P 、S 是I 的3个子集，则阴影部分所表示的集合是（ ）。
A 、（M ∩P ）∩SB 、（M ∩P ）∪SC 、（M ∩P ）∩ðI SD 、（M ∩P ）∪ðI S解：阴影部分是M 与P 的公共部分（转化为集合语言就是M ∩P ），且在S 的外部（转化为集合语言就是ðI S ），故选（C ）。
例2：用集合A 、B 及它们的交集、并集、补集的符号表示阴影部分的集合，正确的表达式是（ ）。
法国天文学家henon映射-概述说明以及解释1.引言1.1 概述在这一部分，我们将介绍法国天文学家Henon映射的概念及其重要性。
Henon映射是一种动力系统，被广泛运用于天文学和混沌理论中。
通过Henon映射，我们可以更好地理解动力系统中的非线性行为，探索天体运动的复杂性和深度。
本文将探讨Henon映射的数学原理及其在天文学中的应用，并展望未来Henon映射的研究方向。
通过对Henon映射的深入研究，我们可以更好地认识宇宙的奥秘，推动天文学领域的发展。
Henon映射的引入为我们揭示宇宙的奥秘提供了新的视角和方法，对于推动科学技术的发展和人类认知世界的进步具有重要意义。
1.2文章结构1.2 文章结构本文将首先介绍Henon映射的概念，包括其起源、定义和基本特性。
接着将深入探讨Henon映射的数学原理，包括其迭代公式、分岔图和混沌特性等方面。
然后将重点讨论Henon映射在天文学中的应用，包括如何通过Henon映射模拟星系运动、探索银河系结构等方面。
最后，我们将总结Henon映射在天文学中的重要性，并展望未来可能的研究方向。
通过本文的介绍，读者将对Henon映射有一个全面的了解，并对其在天文学领域的应用有更深入的认识。
1.3 目的:本篇文章旨在深入探讨法国天文学家Henon映射的概念、数学原理和在天文学中的应用。
通过对Henon映射的研究和探讨，我们旨在增进对这一重要数学工具在天文学领域中的意义和作用的理解，并探讨其在复杂系统中的应用和潜在的未来发展方向。
同时，本文也旨在向读者介绍Henon映射的基本概念和原理，让读者对这一重要的数学工具有一个清晰的认识。
通过对Henon映射的深入探讨，我们希望读者能够进一步认识到其在天文学和其他领域中的重要性，并在未来的研究中能够更好地应用和发展这一工具。
2.正文2.1 Henon映射的概念Henon映射是由法国著名天文学家Michel Henon于1976年提出的一种非线性动力系统。
混沌映射及其应用研究第一章引言混沌映射是一种非线性、混沌现象十分明显的映射，其研究在理论与应用上都有着广泛的关注和应用，包括密码学、信息处理、数字信号处理、图像压缩等领域。
随着科技的不断进步，混沌映射在信息与通信领域的应用越来越广泛，成为一种重要的研究方向。
本文将对混沌映射理论、性质以及应用领域等进行详细讨论。
第二章混沌映射理论混沌映射的研究始于20世纪60年代，是研究全息照相中杂乱光的现象时，由美国物理学家莱耳·约翰逊（E. L. Lorenz）提出。
混沌映射是指一种具有混沌现象的非线性映射，可以简单地表示为一个迭代的函数。
一般而言，混沌映射可以被形式化地表示为：Xn+1=f(Xn)其中，Xn是第n次迭代的值，Xn+1是Xn在下一次迭代后的值，f表示迭代函数。
混沌映射的混沌现象表现在迭代次数增加时，系统的演化呈现出无规律性，即原始状态对系统的演化结果影响极大，微小扰动也会对系统的演化结果产生显著的影响。
混沌映射广泛存在于自然界中，例如流体力学中的Navier-Stokes方程、经典物理中的Henon映射等。
第三章混沌映射性质混沌映射作为非线性映射，在理论模型与实际应用领域都具有许多重要特性。
混沌映射的一般特性包括极度敏感依赖于初始条件、周期运动、奇变现象、自相关和高维混沌等。
3.1 极度敏感依赖于初始条件混沌映射的极度敏感依赖于初始条件是其最为重要的特性之一。
由于基于迭代函数的计算方式，系统的演化对初始状态有着非常高的敏感性，微小的扰动会导致系统最终的演化结果与原始的演化结果存在极大的差异。
3.2 周期运动混沌映射并非没有规律性，在一定的条件下，会呈现出周期运动。
周期运动指的是一些状态在经过一定次数的迭代得到之后，会出现周期性的状态转化，即循环出现相同的状态集。
周期运动是混沌映射在实际应用中的关键特性之一。
3.3 奇变现象混沌映射还具有奇变现象，即在某些情况下，当系统的某个参数发生无限的微小变化时，混沌映射的演化结果将快速发生剧烈的变化，即小扰动会导致混沌映射的演化结果发生“突变”。
中国和希腊的神话故事是最早出现“混沌”一词的，从此之后随着人类文明的进步，文化和科技的发展，中外的文学、艺术、宗教典籍和科学著作早已不断采用“混沌”一词。
“混沌”的英文翻译为“chaos”。
到了近代，特别是近几十年，混沌”一词在各类报刊文章、文献中出现的频率极高。
很多学者认为二十世纪继相对论、量子力学之后的又一次物理学革命就数混沌学了。
法国伟大的数学、物理学家庞加莱（H. Poincare）是研究混沌的第一人, 他在研究太阳系的稳定问题时，猜想能否用数学来证明，从而发现了即使只有三个星体的模型，还是能够产生明显的随机结果。
于是，庞加莱在1903年提出了庞加莱猜想。
庞加莱把拓扑学和动力系统有机地结合，并提出了三体问题在一定范围内，其解是随机的。
到1954，前苏联的概率论大师柯尔莫哥洛夫（Kolmogorov）发表的《哈密顿（Hamilton）函数中微小变化时条件周期运动的保持》一文成为了KAM定理的雏形。
到了1963 年, 柯尔莫哥洛夫的学生，年轻的、具有超群才华的V.I.Arnold 对此给出了严格的数学证明, 基本上在同一时间, 瑞士数学家J.Moser 对此给出了改进表述, 并独立地作出了数学证明。
此文的思想为混沌未发生之初，在保守系统中如何出现混沌提供了信息。
这也为早期明确不仅好散系统有混沌，而且保守系统也有混沌的理论铺平了道路。
1963 年，美国的气象学家、物理学家E.N.Lorenz，对描述大气对流模型的一个完全确定的三阶常微分方程组进行数值仿真时，发现在某些条件下可以出现非周期的无规则行为。
这一结果解释了长期天气预报为什么始终没有获得成功的原因，其根本原因为有一种混沌运动存在于确定非线性动力系统中。
E.N.Lorenz 不仅发觉了第一个奇怪吸引子——Lorenz吸引子，而且还揭示了混沌运动的其他一些基本特征。
这个三阶常微分方程组即著名的洛仑兹系统方程组：（1963 年，美国气象学家 E.N.Lorenz发表了著名的论文《确定性非周期流》，他在论文中指出：在三阶非线性自治系统中可能出现非周期的无规则行为。
