集合的子集与真子集的区别与联系(图文介绍)

§1.2子集与真子集【学习目标】：1 •理解子集、真子集的概念：会判断和证明两个集合的包含关系：2.会判断简单集合的相等关系【教学过程】：—、复习回顾：集合的表示法及有关数集符号N. Z、Q、R・二讲授：'观察下而几组集合A与B,并比较它们之间有怎样的关系：(1)A={-1,1}, B= {-1,0,1,2}(2)A=N, B=R(3)A={xlx为南通人}, B={x\x为中国人}1.子集的概念及记法：如果集合A的任意一个元素都是集合B的元素，即_________________ ,则称集合A为集合B的子集(subset),记为或 ___________ ,读作“—或—” .符号语言可表示为：_____________________图形语言可表示为：_____________________注意：(1)A是B的子集的含义：任意xGA,能推出xGB；(2)不能理解为子集A是B中的“部分元素”所组成的集合.试一试，举个子集例子 ___________________________________2.子集的性质：@ AcA :② 0^A；③AcC想一頑与3匸A能否同R?成立?一着能A与花的关系是什么？3.集合相等： _______________________ ____________________________4.真子集的概念及记法：如果并且__________________ ,这时集合A称为集合B的真子集(proper set),记为____ 或_____,读作“—________ - ________ ”或“ ____ _________ _____ ”符号语言可表示为：_____________________图形语言可表示为：_____________________试一试，举个真子集例子__________________________________5.真子集的性质：①0是任何非空集合的真子集，符号表示为 ______ _____________②真子集具备传递性，符号表示为—_________ ______________三、典例欣赏例1.下列各组的三个集合中，哪两个集合之间具有包含关系：(1)S={-2-1,1,2}, A={-1,1}, B={-2,2)(2)S=R, A={xl x<0,x e /?}, B={x I x > 0,x e R}(3)S={xlx为地球人}, A={xlx为中国人}，B={xlx为外国人}5.下列式子中错误的是 ________________________(4) 0G {x xW10} (5) 0CZ {x xW10} (7) {4, 5, 6, 7}(Z {2, 3, 5, 7. 11} (8) {4, 6. 下列各题中，指出关系式ACB. A ：B 、A^B,A^B. A 二B 中哪些成立：(1)A= (1, 3, 5, 7}, B 二{3, 5, 7} 答： ____________________________________ ・ (2) A= {1, 2, 4, 8), B 二{x x 是 8 的正约数} 答: ____________________________ .7. 如果 P = {X I2X 2-7X <-5}, e = {xl0<x<10),那么 P ________________ Q°8. 设非空集合Ay {1,2,3,4,5,6,7},当aeA 时，必有8-awA,这样的A 有 ____________ 个. 9. 详细列出三元集A={1,2, 3}的所有子集，所有真子集，所有非空真子集.10. 已知集合 A = {x \ X 2 +x-6 = 0} 9 B = {x\ax + \ = 0),若B 匚 A ,求么。

第1讲 集合、子集、真子集、补集1.集合的有关概念①定义:在一定范围内某些确定的、不同的对象的全体叫集合；集合中的每个对象叫集合的元素。

②元素的三要素:集合中的元素具有确定性、互异性和无序性。

③常用数集:自然数集:N ；正整数集:*N N +或；整数集:Z ；有理数集:Q ；实数集:R 。

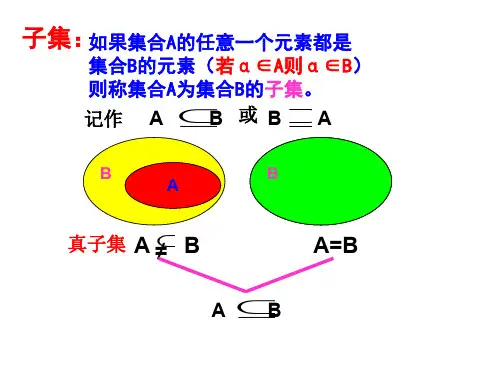
2.子集定义:A 中的任何元素都属于B ，则A 叫B 的子集；记作:A ⊆B 。

3.真子集定义:A 是B 的子集 ，且B 中至少有一个元素不属于A ；记作:B A ⊂。

4.补集定义:设S 是一个集合，A 是S 的一个子集（即S A ⊆），由S 中所有不属于A 的元素组成的集合，记作:},|{A x U x x A C U ∉∈=且。

5.子集个数:n 元集（例如},,{21n a a a A =）有n 2个子集；有n 21-个真子集；有n21-个非空子集；有n 22-个非空真子集。

如:满足{}{}n A ,,3,2,13,2,1 ⊆⊆的集合A 的个数为32-n 。

6.子集与真子集性质：①若A B B A ⊆⊆,则A=B ； ②若C B B A ⊆⊆,，则C A ⊆。

【例1】集合元素性质1.设{}2,3,4aa A -=,且9∈A,求实数a 的值； 2.已知2是集合{}x x x -,,,12中的元素,试求出x 的值。

3.已知集合{}012|2=++=x ax x A 。

①若A 是空集,求a 的取值范围；②若A 是单元素集,求a 的值； ③若A 中至多只有一个元素,求a 的取值范围。

【例2】集合的子集、真子集与补集。

1.集合{}52≤≤-=x x A ，{}121|-≤≤+=m x m x B ，①当Z x ∈时，求A 的非空真子集的个数；②若Z x ∈，A B ≤,求实数m 的取值范围。

2.已知集合{}06|2=-+=x x x P ，{}01|=+=ax x S ，若P S ⊆，求实数a 的值；3.已知集合{}213|+<<-=a x a x A ，{}53|≤≤=x x B ，若B A ⊆，求a 的范围。

高中数学知识总结高中数学集合知识总结高中数学集合知识总结如下：一、集合间的关系1.子集：如果集合A中所有元素都是集合B中的元素，则称集合A为集合B的子集。

2.真子集：如果集合AB，但存在元素a∈B,且a不属于A,则称集合A是集合B的真子集。

3.集合相等：集合A与集合B中元素相同那么就说集合A与集合B相等。

子集：一般地，对于两个集合A与B，如果集合A的任何一个元素都是集合B的元素，我们就说集合A包含于集合B，或集合B包含集合A，记作：AB(或BA)，读作“A包含于B”(或“B包含A”)，这时我们说集合是集合的子集，更多集合关系的知识点见集合间的基本关系二、集合的运算1.并集并集：以属于A或属于B的元素为元素的集合称为A与B的并(集)，记作A∪B(或B∪A)，读作“A并B”(或“B并A”)，即A∪B={x|x∈A,或x∈B}2.交集交集：以属于A且属于B的元素为元素的集合称为A与B的交(集)，记作A∩B(或B∩A)，读作“A交B”(或“B交A”)，即A∩B={x|x∈A,且x∈B}3.补集三、高中数学集合知识归纳：1.集合的有关概念。

1)集合(集)：某些指定的对象集在一起就成为一个集合(集).其中每一个对象叫元素注意：①集合与集合的元素是两个不同的概念，教科书中是通过描述给出的，这与平面几何中的点与直线的概念类似。

②集合中的元素具有确定性(aA和aA，二者必居其一)、互异性(若aA，bA，则a≠b)和无序性({a,b}与{b,a}表示同一个集合)。

③集合具有两方面的意义，即：凡是符合条件的对象都是它的元素;只要是它的元素就必须符号条件2)集合的表示方法：常用的有列举法、描述法和图文法3)集合的分类：有限集，无限集，空集。

4)常用数集：N，Z，Q，R，N*2.子集、交集、并集、补集、空集、全集等概念。

1)子集：若对x∈A都有x∈B，则AB(或AB);2)真子集：AB且存在x0∈B但x0A;记为AB(或，且)3)交集：A∩B={x|x∈A且x∈B}4)并集：A∪B={x|x∈A或x∈B}5)补集：CUA={x|xA但x∈U}注意：①A，若A≠，则A;②若，，则;③若且，则A=B(等集)3.弄清集合与元素、集合与集合的关系，掌握有关的术语和符号，特别要注意以下的符号：(1)与、的区别;(2)与的区别;(3)与的区别。

真子集与子集的区别
1、定义不同
子集是包括本身的元素的集合；真子集是除元素本身的元素的集合。

2、范围不同
子集：集合A范围大于或等于集合B，B是A的子集。

真子集：集合A范围大于集合B，B是A的真子集。

扩展资料
3、元素不同
子集就是一个集合中的元素，全部都是另一个集合中的元素，有可能与另一个集合相等。

真子集就是一个集合中的元素，全部是另一个集合中的元素，但不存在相等。

举例说明：
设全集I为{1, 2, 3}，则它的子集是{1}、{2}、{3}、{1, 2}、{1, 3}、{2, 3}、{1, 2, 3}、?。

而它的`真子集为{1}、{2}、{3}、{1, 2}、{1, 3}、{2, 3}。

集合，简称集，是数学中一个基本概念，也是集合论的主要研究对象。

集合论的基本理论创立于19世纪，关于集合的最简单的说法就是在朴素集合论（最原始的集合论）中的定义，即集合是“确定的一堆东西”，集合里的“东西”则称为元素。

现代的集合一般被定义为：由一个或多个确定的元素所构成的整体。