第二章拓展提高题解析

第二章综合拓展过综合专题1整式的化简求值1.[2021江苏苏州高新区期中]m2＋2mn=13，3mn＋2n2=21，那么2m2＋13mn＋6n2－44的值为〔〕n互为相反数，化简〔3m－2n)－(2m－3n).3.先化简，再求值：2(a2b＋ab2)－2(a2b－1)－3(ab2＋1)，其中a=－3，b=3.4.先化简，再求值：2xy－12(4xy－8x2y2)＋2(3xy－5x2y2)，其中x，y满足〔x－1)2＋|y＋2|=0.专题2整式的加减在实际生活中的应用5.[2021甘肃天水期末]一辆公交车上原来有乘客(6a－6b)人，中途下去一半乘客，又上来假设干人，使车上共有乘客(10a－6b)人，问上车的乘客是多少人？当a=3，b=2时，上车的乘客是多少人？6.某市要建一条高速公路，其中的一段经过公开招标，某建筑公司中标.在建筑过程中，该公司为了保质保量提前完工，投入了甲、乙、丙三个工程队同时进展施工，经过一段时间后，甲工程队筑路a km，乙工程队所筑的路是甲工程队的2 3多18 km，丙工程队所筑的路是甲工程队的2倍少3 km.请问甲、乙、丙三个工程队共筑路多少千米？假设该段高速公路长为1200 km，当a=300时，他们完成任务了吗？专题3整式规律探究7.观察以下关于x的单项式，探究其规律：x，3x2，5x3，7x4，9x5，11x6，…，按照上述规律，第2021个单项式是〔〕202120212021 x20218.[2021湖南邵阳中考]如下图，以下各三角形中的三个数之间均具有一样的规律，根据此规律，最后一个三角形中y与n之间的关系是〔〕=2n＋1 B.y=2n＋n C.y=2n＋l＋n D.y=2n＋n＋19.如图是用棋子摆成的图案：根据图中棋子的排列规律解决以下问题：〔1〕第4个图中有______枚棋子，第5个图中有______枚棋子；〔2〕猜测第n个图中棋子的数量.〔用含n的式子表示〕素养解读运算能力主要是指在明晰运算对象的根底上，依据运算法那么和运算律解决数学问题的能力，运算能力是解决数学问题的根本手段.逻辑推理是数学的根本思维方式，也是人们学习和生活中经常使用的思维方式.在整式的加减运算中，常常要应用逻辑推理进展判断，在逻辑推理中往往要通过运算，发现规律.在解决问题时，运算能力与逻辑推理并驾齐驱，能更好地解决问题.如第1题，通过整式的加减解决实际生活问题，培养学生的逻辑推理能力和运算能力；第3题，先根据题图计算出每种打包方法使用的绳子长度，再通过整式的減法比拟大小，培养学生的数形结合思想和运算能力. 1.[利用整式的加减解决商业问题]某商贩去水果批发市场买苹果，他上午买了60斤，价格为每斤a 元；下午，他又买了40斤，价格为每斤b2a b ＋元的价格卖完后，发现自己赔了钱，其原因是〔 〕＜＞b C.a≤b D.a≥b2.[整式的大小比拟]假设M=4x 2－2021x ＋2021，N=3x 2－2021x ＋2021，那么M______N.(填“＞〞“＜〞或“=，，〕3.〔关注生活数学〕有一个长方体的邮包，用以下三种不同的方法打包，哪一种方法使用的绳子最短？哪一种方法使用的绳子最长？〔注：a ＋b ＞2c)4.[点运动中定值问题的探究][2021河南济源期中]b 是最小的正整数，且a ，b ，c 满足〔c －6)2＋|a ＋b|=0，请答复以下问题：〔1〕请直接写出a ，b ，c 的值，a=______，b=______，c=______；〔2〕如图，a ，b ，c 在数轴上所对应的点分别为A ，B ，C ，点P 为一动点，其对应的数为x ，当点P 在A ，B 之间运动时，请化简式子：|x ＋1|－|x －1|－2|x ＋5|；(请写出化简过程〕〔3〕在〔1〕，〔2〕的条件下，假设点4以每秒n 〔n ＞0〕个单位长度的速度向左运动，同时，点B 和点C 分别以每秒2n 个单位长度和5n 个单位长度的速度向右运动，假设经过t 秒，点B 与点C 之间的距离为BC.点A 与点B 之间的距离为AB.请问：BC －AB 的值是否随着时间t 的变化而改变？假设变化，请说明理由；假设不变，请求出BC －AB 的值.参考答案过综合【解析】2m2＋13mn＋6n2－44=2m2＋4mn＋9mn＋6n2－44=2(m2＋2mn)＋3(3mn＋2n2)—44=2×13＋3×21—44=26＋63—44=45.应选A.2.【解析】因为m和n互为相反数，所以m＋n=0，所以(3m－2n)－(2m－3n)=3m－2n－2m＋3n=m＋n=0.3.【解析】2(a2b＋ab2)－2(a2b－l)－3(ab2＋1)=2a2b+2ab2－2a2b+2－3ab2－3=2a2b －2a2b＋2ab2－3ab2＋2－3=﹣ab2—1.当a=－3，b=3时，原式=－(－3)×32－1=26.4.【解析】因为〔x－1)2＋|y+2|=0，所以x—1=0，y＋2=0，解得：x=1，y=﹣2.2xy－12〔4xy－8x2y2〕＋2(3xy—5x2y2)=2xy－12×4xy＋12×8x2y2＋2×3xy—2×5x2y2=2xy－2xy＋4x2y2＋6xy－10x2y2=6xy－6x2y2，因为x=1，y=－2，所以原式=6×1×(－2)－6×l2×(—2)2=－12－24=－36，5.【解析】由题意，可得〔10a－6b)－[(6a－6b)－12(6a－6b)]= l0a－6b－3a＋3b=7a—3b，所以上车的乘客是(7a－3b)人.当a=3，5=2时，7a－3b=7×3－3×2=15. 故当a=3，b=2时，上车的乘客是15人.6.【解析】乙工程队所筑的路是〔23a＋18)km，丙工程队所筑的路是(2a－3)km，甲、乙、丙二个工程队共筑路a＋(23a＋18)＋(2a－3)=(113a＋15)(km).当a=300时，113a＋15 =1100＋15=1115，因为1115＜1200，所以当a=300时，他们没有完成任务.7.C【解析】根据题中单项式的系数和次数的特点，可知第n个单项式为(2n－1)x n.所以第2021个单项式是(2×2021－1)x2021=4033x2021.应选C.8.B【解析】观察题中图形，可知三角形左边的数字规律为1，2，…，n，三角形右边的数字规律为2，22，…，2n ，三角形下边的数字规律为1＋2，2＋22， …，n ＋2n ，所以y=2n ＋n.应选B.9.【解析】〔1〕22 32由第1个图中棋子的个数是3＋12，第2个图中棋子的个数是4＋22，第3个图中棋子的个数是5＋32，可知第n 个图中棋子的个数是n ＋2＋n 2，所以第4个图中棋子的个数是6＋42=22，第5个图中棋子的个数是7＋52=32.〔2〕第n 个图中棋子的数量为〔n ＋2＋n 2)枚.过拓展1.B 【解析】由题意，可知该商贩买苹果所花去的本钱是〔60a ＋40b)元，他卖完后得到的钱是2a ＋b ×(60＋40)=50(a ＋b)(元〕.由结果赔了钱，可知50(a ＋b)－(60a ＋40b)=10(b －a)＜0，所以a ＞b.应选B.2.＞【解析】因为M －N=(4x 2－2021x ＋2021)－(3x 2－2021x ＋2021)=4x 2－2021x ＋2021－3x 2＋2021x －2021=x 2＋1＞0，所以M ＞N.3.【解析】第〔1〕种方法使用的绳子的长为4a ＋4b ＋8c ，第〔2〕种方法使用的绳子的长为4a ＋4b ＋4c ，第〔3〕种方法使用的绳子的长为6a+6b ＋4c. 因为a ＋b ＞2c ，所以a ＋b －2c ＞0，所以〔6a ＋6b ＋4c)－(4a ＋4b ＋8c)=6a ＋6b ＋4c －4a －4b －8c=2a ＋2b －4c=2(a ＋b －2c)＞0，以6a ＋6b ＋4c ＞4a ＋4b ＋8c ，又〔4a ＋4b ＋8c)—(4a ＋4b ＋4c)=4a ＋4b ＋8c －4a —4b －4c=4c ＞0，所以4a ＋4b ＋8c ＞4a ＋4b ＋4c ，因此6a ＋6b ＋4c ＞4a ＋4b ＋8c ＞4a ＋4b ＋4c ，所以第〔2〕种方法使用的绳子最短，第〔3〕种方法使用的绳子最长.4.【解析】〔1〕－1 1 6因为b 是最小的正整数，所以b=1，因为〔c －6)2＋|a ＋b|=0，所以c －6=0，a ＋b=0，所以c=6，a=－1，b=1.(2)由题意得－1＜x ＜1，所以x＋1＞0，x－1＜0，x+5＞0，所以|x＋l|－|x－l|－2|x＋5|=x＋1＋x－l－2x－10=－10.(3)BC－AB的值不变.由题意，得BC=(6＋5nt)—(1＋2nt〕=5＋3nt，AB=(1＋2nt)－(﹣1－nt)=2＋3nt，所以BC－AB=(5＋3nt)－(2＋3nt)=5＋3nt－2－3nt=3，所以BC－AB的值不变，且BC－AB=3.。

专题2.10 绝对值（拓展提高）一、单选题1．9-的绝对值是（ ）A ．9B ．9-C ．19D ．19- 【答案】A【分析】利用绝对值的定义直接得出结果即可【详解】解：9-的绝对值是：9故选:A【点睛】本题考查绝对值的定义，正确理解定义是关键，熟记负数的绝对值是它的相反数是重点 2．若|3|7x -=，则x 的值为（ ）A ．4-B ．4C ．10D ．4-或10 【答案】D【分析】先根据题意求出（3-x ）的值，从而不难求出x 的值，注意绝对值等于正数的数有两个．【详解】解：∵|3|7x -=∴37x -=±∴x=-4或10故选：D ．【点睛】此题考查了绝对值，解题的关键是掌握绝对值的意义．3．数轴上表示数m 和2m +的点到原点的距离相等，则m 为（ ）A ．2-B ．2C ．1D ．1- 【答案】D【分析】由数轴上表示数m 和2m +的点到原点的距离相等且2m m +>，可得m 和2m +互为相反数，由此即可求得m 的值．【详解】∵数轴上表示数m 和2m +的点到原点的距离相等，2m m +>，∴m 和2m +互为相反数，∴m +2m +=0，解得m =-1．故选D ．【点睛】本题考查了数轴上的点到原点的距离，根据题意确定出m 和2m +互为相反数是解决问题的关键．4．已知12x -≤≤，则化简代数式|3|2|1|x x --+的结果是（ ）A ．13x -B ．13x +C ．13x --D ．13x -+【答案】A【分析】由于﹣1≤x ≤2，根据不等式性质可得：x ﹣3＜0，x +1≥0，再依据绝对值性质化简即可．【详解】解：∵﹣1≤x ≤2，∴x ﹣3＜0，x +1≥0，∴|3|2|1|x x --+=（3﹣x ）﹣2（x +1）＝﹣3x +1；故选：A ．【点睛】本题考查了不等式性质，绝对值定义和性质，整数加减运算等，熟练掌握并运用绝对值性质化简是解题关键．5．已知|a|＝2，b 2＝25，且ab ＞0，则a ﹣b 的值为（ ）A ．7B ．﹣3C ．3D ．3或﹣3 【答案】D【分析】根据绝对值，乘方的意义求出a 、b 的值，再代入计算即可．【详解】解：因为|a|＝2，所以a ＝±2， 因为b 2＝25，所以b ＝±5， 又因为ab ＞0，所以a 、b 同号，所以a ＝2，b ＝5，或a ＝﹣2，b ＝﹣5，当a ＝2，b ＝5时，a ﹣b ＝2﹣5＝﹣3，当a ＝﹣2，b ＝﹣5时，a ﹣b ＝﹣2﹣（﹣5）＝3，因此a ﹣b 的值为3或﹣3，故选：D ．【点睛】本题主要考查了绝对值的性质和代数式求值，准确计算是解题的关键．6．已知,,a b c 三个数在数轴上的位置如图所示，则下列判断正确的是（ ）A ．0ab >B ．0b c ->C ．||b c c b ->-D ．a b a c ->-【答案】D 【分析】先根据在数轴上，右边的数总比左边的数大，得出b ＜c ＜0＜a ，再由相反数、绝对值的定义以及有理数的加减法法则得出结果．【详解】解：由数轴可得：b ＜c ＜0＜a ，∴ab ＜0，b -c ＜0， ∴b c -=c -b ，a-b 可以看作a ，b 之间的相差的单位长度，c -b 可以看作c ，b 之间的相差的单位长度，∴a -b ＞a -c ，故选：D ．【点睛】本题考查了数轴，绝对值和有理数的运算，能根据数轴得出b ＜c ＜0＜a 是解此题的关键．二、填空题7．数轴上表示3的点到原点的距离是_________ ．【答案】3【分析】理解点到原点的距离等于这个数的绝对值，计算即可【详解】∵|3|=3，∴表示3的点到原点的距离是3，故答案为：3．【点睛】本题考查了数轴上的点，绝对值，准确理解点到原点的距离是这个数的绝对值是解题的关键． 8．若()2210a b -++=，则3a b +=_________．【答案】1【分析】根据非负数的性质列式求出a 、b 的值，然后代入代数式进行计算即可得解．【详解】解：∵()220a -≥，10b +≥且相加得零，∴20a -=，10b +=，解得2a =，1b =-，所以，()3321211a b +=+-=-=． 故答案为：1．【点睛】本题考查了非负数的性质，解题的关键是掌握非负数的性质：几个非负数的和为0时，这几个非负数都为0．9．写出一个负数，使这个数的绝对值小于4______．【答案】-1或-2或-3．【分析】绝对值小于4的数有0,1,2,3，添加负号，得到的数是负数都可以写．【详解】∵数的绝对值小于4，∴绝对值小于4的数有0,1,2,3，添加负号，为负数的有-1，-2，-3，任选一个即可，故答案为：-1或-2或-3．【点睛】本题考查了负数，绝对值，有理数的大小比较，熟练掌握负数，绝对值的定义是解题的关键． 10．三个数,,a b c 是均不为0的三个数，且0a b c ++=，则a b c a b c ++=______________． 【答案】1或-1．【分析】根据绝对值的定义化简即可得到结论．【详解】解：∵三个数a 、b 、c 是均不为0的三个数，且a+b+c=0，∴a ，b ，c 三个数中必有一个或两个负数，①当a ，b ，c 三个数中只有一个负数时，则1111||||||a b c a b c ++=+-=， ②当a ，b ，c 三个数中有两个负数时，1111||||||a b c a b c ++=--+=-， 综上所述：a b c a b c ++=1或-1， 故答案为：1或-1．【点睛】本题考查了绝对值，有理数的除法．能分情况讨论是解题关键．注意互为相反数的两个数商为-1．11．如果一个量的实际值为a ，测量值为b ，我们把a b -称为绝对误差，a b a-称为相对误差．若有一种零件实际长度为5.0cm ，测量得4.8cm ，则测量所产生的绝对误差是_____cm ，相对误差是_____cm ．【答案】0.2 0.04【分析】按照给出的定义计算即可.【详解】解：∵a=5，b=4.8，∴绝对误差是a b -=|5-4.8|=0.2（cm ），∴相对误差是a b a- =5 4.85- =0.04（cm ）.故答案为0.2cm ，0.04cm .【点睛】本题考查了新定义问题,绝对值的计算，理解新定义，并按照要求准确计算是解题的关键. 12．如果|a ﹣2|的值与|b+3|的值互为相反数，那么2b ﹣a ＝_____．【答案】-8【分析】根据相反数的定义和非负数的性质，可求出a 、b 的值，然后代入计算即可．【详解】根据题意得：|a−2|＋|b ＋3|＝0，∴a−2＝0，b ＋3＝0，解得：a ＝2，b ＝−3，则2b−a ＝2×（−3）−2＝−8．故答案为：−8．【点睛】本题考查了相反数的定义和非负数的性质．解题的关键是掌握非负数的性质：几个非负数的和为0时，这几个非负数都为0．13．当a =__________时，式子10|2|a -+取得最大值，()2202321a +-+有最小值为__________．【答案】2- 2023【分析】利用绝对值和偶次方是非负性解答即可．【详解】解：由 10|2|a -+取得最大值，即|2|a +取最小值，∵|2|0a +≥，∴ |2|a +的最小值为0，即2a =-，∴当2a =-时，式子10|2|a -+取得最大值，∵()2210a -+≥，∴22023(21)2023a +-+，故22023(21)a +-+有最小值为2023．故答案为2-、2023．【点睛】本题主要考查了非负数的性质，初中阶段有三种类型的非负数有三类分别是绝对值、偶次方、二次根式（算术平方根）．14．“数形结合”思想在数轴上得到充分体现，如在数轴上表示数5和2-的两点之间的距离，可列式表示为()52--，或25--；表示数x 和3-的两点之间的距离可列式表示为()33x x --=+．已知31239x x y y ++-+++-=，则x y +的最大值为______．【答案】4 【分析】根据题意分别得到31x x ++-和23y y ++-的最小值，结合31239x x y y ++-+++-=得到31x x ++-=4，23y y ++-=5，根据x 和y 的范围得到x+y 的最大值．【详解】解：由题意可得：31x x ++-表示x 与-3的距离和x 与1的距离之和，23y y ++-表示y 与-2的距离和y 与3的距离之和，∴当-3≤x≤1时，31x x ++-有最小值，且为1-（-3）=4，当-2≤x≤3时，23y y ++-有最小值，且为3-（-2）=5， ∵31239x x y y ++-+++-=， ∴31x x ++-=4，23y y ++-=5，∴x+y 的最大值为：1+3=4，故答案为：4．【点睛】本题考查了数轴上两点之间的距离，绝对值的意义，，用几何方法借助数轴来求解，数形结合是解答此题的关键．三、解答题15．已知|x|＝23，|y|＝13，且xy ＜0，求x ﹣y 的值． 【答案】±1． 【分析】根据绝对值的定义，求出x ，y 的值，再由xy ＜0，得x ，y 异号，从而求得x -y 的值．【详解】解：∵|x |=23，|y |=13， ∴x =±23，y =±13，又xy ＜0， ∴x =23，y =-13或x =-23，y =13； 当x =23，y =-13时，x -y =23-（-13）=1； 当x =-23，y =13时，x -y =-23-13=-1； 综上，x -y =±1． 【点睛】本题考查了有理数的乘法、减法和绝对值运算，注互为相反数的两个数的绝对值相等． 16．同学们都知道，|4(2)|--表示4与2-的差的绝对值，实际上也可理解为4与2-两数在数轴上所对应的两点之间的距离：问理|3|x -也可理解为x 与3两数在数轴上所对应的两点之问的距离，试探索： （1）|4(2)|--=_______．（2）找出所有符合条件的整数x ，使|4||2|6x x -++=成立，并说明理由（3）由以上探索猜想，对于任何有理数x ，|3||6|x x -+-是否有最小值？如果有，写出最小值；如果没有，说明理由．【答案】（1）6；（2）-2，-1，0，1，2，3，4，理由见解析；（3）有最小值为3【分析】（1）直接去括号，再按照去绝对值的方法去绝对值就可以了．（2）要x 的整数值可以进行分段计算，令x -4=0或x +2=0时，分为3段进行计算，最后确定x 的值． （3）先得出|x -3|+|x -6|的意义，从而得到x 在3和6之间时（包含3和6）有最小值．【详解】解：（1）原式=|4+2|=6，故答案为：6；（2）令x -4=0或x +2=0时，则x =4或x =-2，当x ＜-2时，∴-（x -4）-（x +2）=6，∴-x +4-x -2=6，∴x =-2（范围内不成立）；当-2＜x ＜4时，∴-（x -4）+（x +2）=6，∴-x +4+x +2=6，∴6=6，∴x =-1，0，1，2，3；当x ＞4时，∴（x -4）+（x +2）=6，∴x -4+x +2=6，∴x =4（范围内不成立），∴综上所述，符合条件的整数x 有：-2，-1，0，1，2，3，4；（3）|x -3|+|x -6|表示数轴上到3和6的距离之和，∴当x 在3和6之间时（包含3和6），|x -3|+|x -6|有最小值3．【点睛】本题是一道去绝对值和数轴相联系的综合试题，考查了取绝对值的方法，取绝对值在数轴上的运用．难度较大．去绝对的关键是确定绝对值里面的数的正负性．17．“分类讨论”是一种重要数学思想方法，下面是运用分类讨论的数学思想解决问题的过程，请仔细阅读，并解答题目后提出的四个问题．例：三个有理数a ，b ，c 满足0abc >，求abca b c ++的值．解：由题意得，a ，b ，c 三个有理数都为正数或其中一个为正数，另两个为负数．①当a ，b ，c 都是正数，即0a >，0b >，0c >时， 则：1113a b c a b c a b c a b c++=++=++=， ②当a ，b ，c 有一个为正数，另两个为负数时，设0a >，0b <，0c <， 则：()()1111a b c a b c a b c a b c--++=++=+-+-=-． 综上，abca b c ++的值为3或-1．请根据上面的解题思路解答下面的问题：（1）已知3a =，1=b ，且a b <，求+a b 的值；（2）已知a ，b 是有理数，当0ab >时，求a b a b+的值． （3）已知a ，b ，c 是有理数，0a b c ++=，0abc <，求a b c a b c ++． 【答案】（1）-2或-4；（2）2±；（3）1【分析】（1）根据绝对值的意义和a ＜b ，确定a 、b 的值，再计算a+b ；（2）对a 、b 进行讨论，即a 、b 同正，a 、b 同负，根据绝对值的意义进行计算即可；（3）根据a ，b ，c 是有理数，a+b+c=0，0abc <，则a ，b ，c 两正一负，然后进行计算即可．【详解】解：（1）因为3a =，1=b ，且a b <，所以3a =-，1b =或1-，则2a b +=-或4a b +=-．（2）①当0a <，0b <时，112a b a b+=--=-； ②当0a >，0b >时，112a b a b+=+=； 综上，a b a b+的值为2±． （3）已知a ，b ，c 是有理数，0a b c ++=，0abc <．所以a ，b ，c 两正一负，不妨设0a >，0b >，0c <， 所以1111a b c a b c++=+-=． 【点睛】考查了绝对值的意义、分类讨论的思想方法．能不重不漏的分类，会确定字母的范围和字母的值是关键；18．综合与实践．结合数轴与绝对值的知识回答下列问题：（1）探究：①数轴上表示6和1的两点之间的距离是 ；②数轴上表示﹣2和﹣7的两点之间的距离是 ；③数轴上表示﹣3和6的两点之间的距离是 ．（2）归纳：一般的，数轴上表示数a和数b的两点之间的距离等于．（3）应用：①如果表示数a和3的两点之间的距离是12，则可记为：|a﹣3|＝12，那么a＝．②若数轴上表示数a的点位于﹣3与6之间，求|a＋3|＋|a﹣6|的值．【答案】（1）①5；②5；③9；（2）|a﹣b|；（3）①﹣9或15；②9【分析】（1）根据数轴上两点之间距离的计算方法得出答案，（2）由特殊到一般，得出结论，（3）①利用数轴上两点距离的计算方法得出答案；②由|a＋3|＋|a﹣6|所表示的意义，转化为求数轴上表示﹣3的点到表示6的点之间的距离．【详解】解：（1）①|6﹣1|＝5，②|﹣2﹣（﹣7）|＝5，③|﹣3﹣6|＝9，故答案为：5，5，9；（2）由数轴上两点距离的计算方法可得，|a﹣b|；故答案为：|a﹣b|；（3）①由题意得，a﹣3＝12或a﹣3＝﹣12，解得，a＝15或a＝﹣9，故答案为：﹣9或15；②|a＋3|表示数轴上表示数a与﹣3的点之间的距离，|a﹣6|表示数轴上表示数a 与6两点之间的距离，当数a的点位于﹣3与6之间时，有|a＋3|＋|a﹣6|＝|3﹣（﹣6）|＝9，故答案为：①﹣9或15，②9.【点睛】本题考查了数轴表示数的意义和方法，理解数轴上两点距离的计算方法是解决问题的关键．19．探索性问题：已知点A，B在数轴上分别表示m、n．（1）填写表：m 5 −5 −6 −6 −10n 3 0 4 −4 2A ，B 两点的距离（2）若A ，B 两点的距离为d ，则d 与m 、n 有何数量关系；（3）在数轴上标出所有符合条件的整数点P ，使它到3和−3的距离之和为6，并求出所有这些整数的和； （4）若点C 表示的数为x ，当C 在什么位置时，23x x ++-取得值最小？【答案】（1）2；5；10；2；12；（2）d ＝|m ﹣n |；（3）作图见详解；0；（4）点C 在点﹣2和点3之间时，|x +2|+|x﹣3|的值最小，其最小值为5．【分析】（1）由题意观察数轴，得出A 、B 两点的距离；（2）根据题意通过观察表格，进行分析写出一般规律；（3）由题意充分运用数轴这个工具，由此表示整数点P ；（4）根据题意在（2）（3）的启发下，结合数轴，进行分析即可回答题目的问题．【详解】解：（1）见表格；m5 ﹣5 ﹣6 ﹣6 ﹣10 n3 04 ﹣4 2 A 、B 两点的距离2 5 10 2 12故答案为：2；5；10；2；12；（2）若A 、B 两点的距离为d ，则d 与m 、n 的数量关系为：d ＝|m ﹣n |；（3）符合条件的整数点P 有7个，如图；所有这些整数和为：﹣3﹣2﹣1+0+1+2+3＝0．（4）|x +2|表示点C 到点﹣2的距离，|x ﹣3|表示点C 到点3的距离，当点C 在点﹣2和点3之间时，|x +2|+|x ﹣3|的值最小，其最小值为：5．【点睛】本题主要考查数轴，绝对值的性质，数轴上两点间的距离．解题的关键是借助数轴，把数和点对应起来，也就是把“数”和“形”结合起来，二者互相补充，相辅相成，把很多复杂的问题转化为简单的问题，在学习中要注意培养数形结合的数学思想．20．阅读材料：我们知道：点A 、B 在数轴上分别表示有理数a 、b ，A 、B 两点之间的距离表示为AB ，在数轴上A 、B 两点之间的距离AB a b ．所以式子3x -的几何意义是数轴上表示有理数x 的点与表示有理数3的点之间的距离；同理4x -也可理解为x 与4两数在数轴上所对应的两点之间的距离． 试探索：（1）若25x ，则x 的值是______________．（2）同理538x x -++=表示数轴上有理数x 所对应的点到5和-3所对应的两点距离之和为8，则所有符合条件的整数x 是_____________．（3）由以上探索猜想，若点P 表示的数为x ，当点P 在数轴上什么位置时，|3||6|x x -+-有最小值？ 如果有，直接写出最小值是多少？【答案】（1）7或3；（2）-3，-2，-1,0,1,2,3,4,5；（3）当36x ≤≤时，36x x -+-取最小值，最小值为3【分析】（1）结合题意，根据数轴的性质分析，即可得到答案；（2）结合题意，根据数轴的性质分析，即可得到答案；（3）根据（2）的结论，根据数轴的性质分析，即可完成求解．【详解】（1）根据题意得：527x =+=或523-=故答案为：7或3；（2）∵数轴上点到5到点-3的距离为：()538--=当x 在点-3左侧时，58x -> ∴538x x -++>；当x 在点5右侧时，38x +> ∴538x x -++>；∴符合条件的整数x 范围为：35x -≤≤∴所有符合条件的整数x 为：-3，-2，-1,0,1,2,3,4,5故答案为：-3，-2，-1,0,1,2,3,4,5；（3）根据（2）的结论，当x 在点3左侧时，63x -> ∴363x x -+->；当x 在点6右侧时，33x ->∴363x x -+->；当36x ≤≤时，633x x +-=-∴当36x ≤≤时，36x x -+-取最小值，最小值为3．【点睛】本题考查了有理数的知识；解题的关键是熟练掌握绝对值、数轴的性质，从而完成求解．。

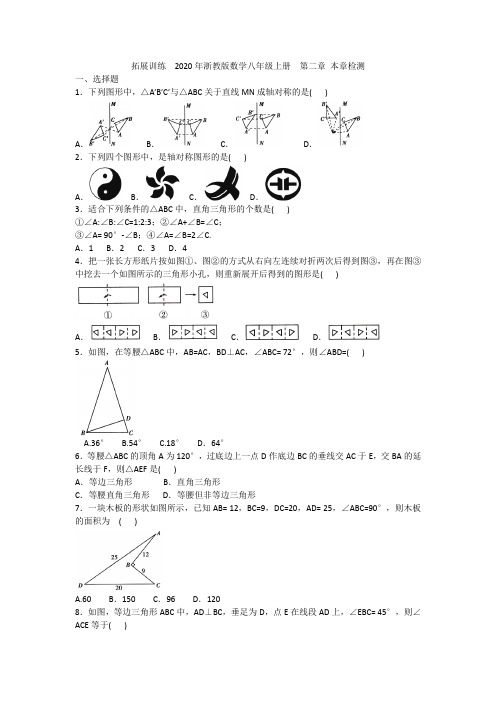
拓展训练2020年浙教版数学八年级上册第二章本章检测一、选择题1．下列图形中，△A’B’C’与△ABC关于直线MN成轴对称的是( )A．B．C．D．2．下列四个图形中，是轴对称图形的是( )A．B．C．D．3．适合下列条件的△ABC中，直角三角形的个数是( )①∠A:∠B:∠C=1:2:3；②∠A+∠B=∠C；③∠A= 90°-∠B；④∠A=∠B=2∠C.A．1 B．2 C．3 D．44．把一张长方形纸片按如图①、图②的方式从右向左连续对折两次后得到图③，再在图③中挖去一个如图所示的三角形小孔，则重新展开后得到的图形是( )A．B．C．D．5．如图，在等腰△ABC中，AB=AC，BD⊥AC，∠ABC= 72°，则∠ABD=( )A.36°B.54°C.18°D．64°6．等腰△ABC的顶角A为120°，过底边上一点D作底边BC的垂线交AC于E，交BA的延长线于F，则△AEF是( )A．等边三角形B．直角三角形C．等腰直角三角形D．等腰但非等边三角形7．一块木板的形状如图所示，已知AB= 12，BC=9，DC=20，AD= 25，∠ABC=90°，则木板的面积为( )A.60 B．150 C．96 D．1208．如图，等边三角形ABC中，AD⊥BC，垂足为D，点E在线段AD上，∠EBC= 45°，则∠ACE等于( )A.15°B.30°C.45°D.60°9.如图,在△ABC 中,∠BAC=90°，点D 在BC 延长线上，且AD=21BC ，若∠D=40°，则∠B=( )A.10°B.20°C.30°D.40°10.如图，在△ABC 中，AB=AC ，D 、E 是△ABC 内的两点，AD 平分∠BAC ，∠EBC=∠E= 60°．若BE=6 cm ，DE =2 cm ，则BC 的长为( )A.4 cmB.6 cmC.8 cmD.12 cm二、填空题11.若直角三角形中两个锐角的度数比为1:2，则这两个锐角中，较大锐角的度数为______°．12.夷陵长江大桥为三塔斜拉桥，如图，中塔左右两边所挂的最长钢索AB=AC ，A 与塔柱底端D 的连线平分∠BAC ，且塔柱底端D 与点B 间的距离是228米，则BC 的长是_______米.13.一个等腰三角形的底边长为5，一腰上的中线把它的周长分成的两部分的差为2，则这个等腰三角形的腰长为__________.14．如图，点D 在△ABC 的边BC 上，且BC= BD+AD ．则点D 在AC 的_____上.15.命题“在同一个三角形中，等角对等边”的逆命题是______________. 16.下图是一段楼梯，高BC 是3米，斜边AC 是5米，若在楼梯上铺地毯，则至少需要地毯__________米．17.如图，在△ABC中，已知∠BAC= 108°，∠B=36°，且CA= CD，则图中共有_______个等腰三角形．18.如图，△ABC中，AB=AC，DE垂直平分AB，BE⊥AC，AF⊥BC，则∠EFC=________．三、解答题19.如图，△ABC中，AB=AC，小聪同学利用直尺和圆规完成了如下操作：①作∠BAC的平分线AM交BC于点D；②作边AB的垂直平分线EF，EF与AM相交于点P；③连结PB，PC.请你观察图形解答下列问题：(1)线段PA，PB，PC之间的数量关系是____，(2)若∠ABC= 70°，求∠BPC的度数．20.如图，在等腰直角三角形ABC中，∠ABC= 90°，D为AC边上中点，过D点作DE⊥DF，交AB于E，交BC于F，若AE=4，FC=3，求EF的长．21.如图．在△ABC中，AD是△ABC的高，作∠DCE= ∠ACD，交AD的延长线于点E，点F 是点C关于直线AE的对称点，连结AF.(1)求证：CE =AF；(2)若CD=1，AD=3，且∠B=20°，求∠BAF的度数．22.如图，P是等边三角形ABC内的一点，连结PA，PB，PC，以BP为边作∠PBQ=60°，且BP=BQ，连结CQ.(1)观察并猜想AP与CQ之间的大小关系，并说明理由；(2)若PA =3，PB=4，PC=5，连结PQ，判断△PQC的形状并说明理由．23.如图，已知点O到△ABC的两边AB、AC的距离相等，且OB= OC.(1)如图①，若点O在BC上，求证：△ABC是等腰三角形；(2)如图②，若点O在△ABC内部，求证：AB=AC；(3)若点O在△ABC的外部，AB=AC还成立吗？请画图说明．本章检测一、选择题1.B根据轴对称的概念，沿直线MN折叠，△A'B'C’与△ABC能够完全重合的只有选项B．2.D D项中的图案沿水平居中的一条铅垂线对折，左右两边的部分能够互相重合，所以它是轴对称图形，故选D．3.C ①设∠A=x°，∠B=2x°，∠C=3x°，则x+2x+3x= 180，x=30，∴∠C=3x°= 90°；②∵∠A+∠B+∠C= 180°，∠A+∠B=∠C，∴2∠C= 180°，∠C=90°；③∵∠A= 90°-∠B，∴∠A+∠B=90°，∴∠C= 180°-(∠A+∠B)= 90°；④由∠A+∠B+∠C=180°，∠A=∠B=2∠C，得2∠C+2∠C+∠C=180°，∠C= 36°，∠A=∠B=72°．故选C．4.C选项A、B中的图形不符合以折痕所在直线为对称轴的特征，选项C、D中的图形都符合以折痕所在直线为对称轴的特征，但选项D中的图形的三角形小孔的位置与题意不符，只有C与之吻合（如图）．故选C．5.B在△ABC中，∵AB= AC，∴∠C=∠ABC= 72°，∴∠A=180°-∠ABC-∠C=36°，又BD⊥AC ，∴∠ADB= 90°，在△ABD 中，∠ABD= 180°-90°-36°= 54°．故选B ．6.A 如图，∵AB=AC ，∴∠B=∠C ．∵∠AEF= ∠DEC= 90°-∠C ，∠F= 90°-∠B ，∴∠AEF=∠F ．即AE=AF ，又∵∠BAC= 120°，∴∠FAE= 60°，∴△AEF 是等边三角形，故选A ．7.C 如图，连结AC ，∵∠ABC=90°，∴△ABC 为直角三角形，在Rt △ABC 中，．在△ADC 中，∵AC ²+DC ²= 15²+20²= 625= 25²= AD ²，△ADC是直角三角形．∴木板的面积=21×20×15-21×12×9= 96．故选C ．8.A 在等边三角形ABC 中，∵AD ⊥BC ，∴BD= CD ，即AD 所在的直线是BC 的垂直平分线，∵点E 在AD 上，∴BE= CE ，∴∠EBC=∠ECB ，∵∠EBC=45°，∴∠ECB=45°，∵△ABC 是等边三角形，∴∠ACB= 60°，∴∠ACE= ∠ACB-∠ECB=15°．故选A ．9.B 如图，取BC 的中点E ，连结AE ．∵∠BAC= 90°，点E 是BC 的中点，∴AE =21BC= BE ，∴∠B=∠EAB ，∵AD=21BC ，∴AE=AD ，∴∠AED= ∠D=40°，∴∠B=20°．故选B.10.C 如图，延长ED 交BC 于M ，延长AD 交BC 于N ，∵AB=AC ，AD 平分∠BAC ，∴AN ⊥BC ，BN= CN ，∵∠EBC=∠E=60°，∴△BEM 为等边三角形，∵BE =6 cm ，DE=2 cm ，∴DM=4 cm ．∵△BEM 为等边三角形，∴∠EMB=60°，∵AN ⊥BC ，∴∠DNM=90°，∴∠NDM=30°∴NM=2 cm.∴BN=4 cm ，∴BC= 2BN=8 cm ．故选C ．二、填空题解析 ．12．答案 456解析 根据题意，知此三角形是等腰三角形，又等腰三角形顶角的平分线所在直线是其对称轴，∴点B 与点C 关于AD 所在的直线成轴对称，∴BC=2BD=456米．13．答案14.答案 垂直平分线解析 由BC= BD+DC= BD+AD ，得AD= CD ，∴D 在AC 的垂直平分线上．15．答案 在同一个三角形中，等边对等角解析 命题“在同一个三角形中，等角对等边”可以改写为“在同一个三角形中，如果两个角相等，那么它们所对的边相等”，交换此命题的条件和结论后为“在同一个三角形中，如果两条边相等，那么它们所对的角相等”，即“在同一个三角形中，等边对等角”．16．答案7解析 ∵△ABC 是直角三角形，BC=3米，AC=5米，∴AB=（米）．如果在楼梯上铺地毯，那么至少需要地毯4+3 =7米．17．答案 3解析 在△ABC 中，∵∠BAC= 108°，∠B=36°，∴∠C=36°，∴∠B=∠C ．∴AB=AC ． 在△ACD 中，∵CA= CD ，∴∠CAD=∠CDA=21×（180°-36°）=72°． ∴∠DAB= ∠CDA-∠B=36°，∴∠DAB= ∠B ，∴AD=BD ，∴等腰三角形有△ADB 、△ABC 、△ADC ．共3个．18.答案 45°解析 ∵DE 垂直平分AB ，∴AE= BE.又∵BE ⊥AC ，∴△ABE 是等腰直角三角形．∴∠BAE= 45°．又∵AB=AC ，AF ⊥BC ．∴∠ABC= ∠C=67.5°，BF=FC=21BC. ∴在Rt △BCE 中，EF 是BC 边上的中线，∴EF ＝21BC ＝CF ， ∴∠FEC=∠FCE=67.5°，∴∠EFC=45°.三、解答题19．解析 (1) PA =PB= PC ，理由：∵AB=AC ，AM 平分∠BAC ．∴PB=PC(等腰三角形三线合一)．∵EP 是AB 的垂直平分线，∴PA= PB ，∴PA=PB=PC ．(2)∵AB=AC ，∠ABC=70°，∴∠ABC= ∠ACB=70°（等边对等角）．∴∠BAC= 180°-2×70°=40°．∵AM 平分∠BAC ，∴∠BAD=∠CAD=20°．∴∠ABP= ∠BAP= ∠ACP=20°．∴∠BPC= ∠ABP+∠BAC+ ∠ACP= 20°+40°+20°= 80°.20．解析 连结BD ．∵等腰直角三角形ABC 中，D 为AC 边上的中点，∴BD ⊥AC ，BD=CD=AD ，∠BDC=90°，∠ABD= ∠CBD= 45°，又∵∠C=45°，∴∠DBE= ∠DCF=45°．∴BD= CD. 又∵DE ⊥DF ，∴∠EDF= 90°，∴∠FDC=∠EDB ，∴△EDB ≌△FDC ，∴BE=CF=3，∴AB=AE+BE=7，则BC=7，∴BF=BC-FC=7-3=4.在Rt △EBF 中，EF ²=BE ²+BF ²=3²+4²=25，∴EF=5.21．解析 (1)证明：∵AD 是△ABC 的高，∴∠ADC=∠EDC=90°，又∠DCE= ∠ACD ，∴∠DAC=∠E ，∴△ACE 为等腰三角形，∴AC= CE ，∵点F 是点C 关于直线AE 的对称点，∴AF=AC ，∴CE=AF.(2)在Rt △ACD 中，CD=1，AD=3，根据勾股定理得， ∴CD=21AC ，∴∠DAC= 30°. 同理可得∠DAF= 30°，在Rt △ABD 中，∠B= 20°，∴∠BAF=90°-∠B-∠DAF=40°.22．解析 (1)AP=CQ ．理由如下：∵∠ABP+∠CBP= 60°，∠PBQ=∠CBQ+∠CBP= 60°，∴∠CBQ=∠ABP ，在△ABP 和△CBQ 中，∴△ABP ≌△CBQ （SAS ），∴AP= CQ.(2)∵∠PBQ= 60°，且BQ=BP ，∴△BPQ 为等边三角形，在等边△ABC 和等边△BPQ 中，∵PB=PQ=4，PA=QC=3，PQ ²+CQ ²=PC ²，∴△PQC 为直角三角形（勾股定理逆定理）．23．解析 (1)证明：如图，过O 作OE ⊥AB 于E ，OF ⊥AC 于F ，则∠OEB=∠OFC=90°． ∵点O 到△ABC 的两边AB 、AC 的距离相等．∴OE =OF.在Rt △OEB 和Rt △OFC 中．∴Rt △OEB ≌Rt △OFC( HL)，∴∠ABC=∠ACB ．∴AB=AC ．即△ABC 是等腰三角形（等角对等边）．(2)证明：如图，过O作OE⊥AB于E，OF⊥AC于F，则∠OEB=∠OFC=90°，∵点O到△ABC的两边AB、AC的距离相等，∴OE=OF．在Rt△OEB和Rt△OFC中，∴Rt△OEB≌Rt△OFC(HL) ，∴∠ABO= ∠ACO，又∠OBC=∠OCB，∴∠ABC= ∠ACB，∴AB=AC.(3)AB=AC不一定成立．理由：①当∠A的平分线所在直线和BC的垂直平分线重合时，如图，过O作OE⊥AB交AB 的延长线于E，OF⊥AC交AC的延长线于F，则∠OEB= ∠OFC=90°．∵点O到△ABC的两边AB、AC的距离相等，∴OE=OF．在Rt△OEB和Rt△OFC中，∴Rt△OEB≌Rt△OFC ( HL) ，∴∠EBO=∠FCO，∵OB=OC，∴∠OBC =∠OCB，∵∠ABC=180°-(∠OBC+∠EBO)，∠ACB= 180°-(∠OCB+∠FCO)，∴∠ABC=∠ACB，∴AB=AC；②当∠A的平分线和BC的垂直平分线不重合时，如图，此时∠ABC和∠ACB不相等，∴AB ≠AC．综上．AB=AC不一定成立．。

专题2.12 有理数的加法（拓展提高）一、单选题1．实数a 在数轴上的对应点的位置如图所示，若实数b 满足0a b +>，则b 的值可以是（ ）A ．1-B ．0C ．1D ．2【答案】D【分析】根据0a b +>确定出0b >且b a >，进而确定出b 的范围，判断即可． 【详解】解：∵0a b +>，21a -<<-， ∴0b >，而且1b a >>， ∴1b a >->， 符合条件是D ，b =2． 故选：D ．【点睛】本题考查了有理数加法的运算法则和数轴上的点和有理数的对应关系．解决本题的关键是根据加法的符号规律确定b 的取值范围．2．有理数m ，n ，k 在数轴上的对应点的位置如图所示，若m +n ＜0，n +k ＞0，则A ，B ，C ，D 四个点中可能是原点的是（ ）A ．A 点B ．B 点C ．C 点D ．D 点【答案】B【分析】分四种情况讨论，利用数形结合思想可解决问题．【详解】解：若点A 为原点，可得0＜m ＜n ＜k ，则m +n ＞0，与题意不符合，故选项A 不符合题意； 若点B 为原点，可得m ＜0＜n ＜k ，且|m |＞n ，则m +n ＜0，n +k ＞0，符合题意，故选项B 符合题意； 若点C 为原点，可得m ＜n ＜0＜k ，且|n |＞|k |，则n +k ＜0，与题意不符合，故选项C 不符合题意； 若点D 为原点，可得m ＜n ＜k ＜0，则n +k ＜0，与题意不符合，故选项D 不符合题意； 故选：B ．【点睛】本题主要考查了与数轴有关的计算，数形结合进行判断是解题的关键．3．已知a ，b ，c 为非零有理数，则a b ca b c++的结果可能值的个数为（ ） A ．2 B ．3C ．4D ．5【答案】C【分析】由绝对值的性质可知a a ，b b ，cc这三个式子的值是±1，分情况讨论求出结果即可． 【详解】解：∵a ，b ，c 为非零有理数，∴它们的绝对值可能是自己本身，也可能是自己的相反数， ∴1aa=±， 同理1b b =±，1c c=±， ∴1113a ca b cb ++=++=， 1113a b ca b c++=---=-， 1111a b ca b c++=--=-， 1111a b ca b c++=+-=， 一共有4种结果． 故选：C ．【点睛】本题考查绝对值的性质，解题的关键是掌握绝对值的性质． 4．如果0a b +<，且0b >，那么a b a -、、、b -的大小关系是（ ）A ．a b a b <<-<-B ．a b b a <-<<-C ．a b a b <-<-<D ．b a a b -<<-< 【答案】B【分析】根据题目条件分析出a 是负数，且a 的绝对值大于b 的绝对值，即可比较大小． 【详解】解：∵0a b +<，且0b >， ∴0a <，且a b >， ∴a b b a <-<<-． 故选：B ．【点睛】本题考查有理数加法的运算法则和有理数的大小比较，解题的关键是掌握有理数的加法运算法则． 5．如图，有理数a ，b ，c ，d 在数轴上的对应点分别是A ，B ，C ，D ，若5b d +=，则a c +（ ）A ．大于5B ．小于5C ．等于5D ．不能确定【答案】A【分析】根据数轴，判断出数轴上的点表示的数的大小，进而可得结论 【详解】解：由数轴可得，a ＞d ，c ＞b ， ∴a+c ＞b+d ∵b+d=5 ∴a+c ＞5 故选：A【点睛】本题考查数轴、有理数加法法则以及有理数的大小比较，属于中等题型． 6．把所有正整数从小到大排列，并按如下规律分组：（1），(2， 3， 4)，(5，6，7，8，9)，(10， 11，12， 13， 14， 15， 16)，…，现用等式 A M =(i ，j)表示正整数 M 是第i 组第 j 个数(从左往右数)，如A 8=(3，4)，则A 2020=( ) A ．(44，81) B ．(44，82)C ．(45，83)D ．(45，84)【答案】D【分析】根据排列规律，先判断2020在第几组，再判断是这一组的第几个数即可求解； 【详解】设2020在第n 组，组与组之间的数字个数规律可以表示为：2n-1 则1+3+5+7+⋅⋅⋅+(2n-1)=12×2n×n=2n ， 当n=44时，21936n = ， 当n=45时，22025n =，∴ 2020在第45组，且2020-1936=84，即2020为第45组的第84个数； 故选：D ．【点睛】本题考查数字类的规律探究、有理数的加法运算，善用联想探究数字规律是解决此类问题的常用方法；二、填空题7．绝对值大于﹣12且小于13的所有整数的和是_______． 【答案】0．【分析】首先根据有理数大小比较的方法，可得：绝对值大于-12且小于13的所有整数有：±12、±11、±10、±9、±8、±7、±6、±5、±4、±3、±2、±1、0，求它们的和即可．【详解】解：∵绝对值大于-12且小于13的所有整数有：±12、±11、±10、±9、±8、±7、±6、±5、±4、±3、±2、±1、0，因为互为相反数的两个数的和是0，所以绝对值大于﹣12且小于13的所有整数的和是0． 故答案为：0．【点睛】本题考查了绝对值和有理数的加法，解题关键是理解绝对值的意义，知道互为相反数的两个数和为0．8．如果0ab >，那么a abb ab ab++=________． 【答案】3或−1．【分析】由ab ＞0，则a 、b 同号，再根据绝对值的性质计算即可． 【详解】∵ab ＞0， ∴a 、b 同号， 当a ＞0，b ＞0时，a ab b a b ab++=1＋1＋1＝3； 当a ＜0，b ＜0时，a ab b ab ab++=−1−1＋1＝−1； 故答案为：3或−1．【点睛】本题考查化简绝对值，熟练掌握有理数绝对值的性质是解题的关键． 9．绝对值不大于100的所有整数的和是_____________． 【答案】0【分析】找出所有绝对值不大于100的数，再将它们相加即可解答.【详解】解：绝对值不大于100的所有整数有-100、-99、-98…-1、0、1、2、3、…99、100， ∴和为：-100+（-99）+（-98）+…+（-1）+0+1+2+3+…+99+100=（-100+100）+（-99+99）+…+（-1+1）+0=0．故答案为0．【点睛】本题考查了绝对值和有理数的运算，解题的关键是找出所有绝对值不大于100的数.10．计算：|12－1|＋|13－12|＋|14－13|＋…＋|199－198|＋|1100－199|＝___________．【答案】99 100【分析】先根据绝对值的性质化简，再从第二项开始依次相加即可得出结果．【详解】解：原式=111111111 1...22334989999100 -+-+-++-+-=1 1100 -=99 100，故答案为：99 100．【点睛】本题考查化简绝对值，有理数的加法．在本题中应先化简，再计算．11．如图，是某剧场第一排座位分布图．甲、乙、丙、丁四人购票，所购票数分别为1，3，5，6．每人选座购票时，只购买第一排的座位相邻的票，同时使自己所选的座位之和最小．如果按“甲、乙、丙、丁”的先后顺序购票，那么甲购买1号座位的票，乙购买2，4，6号座位的票，丙购买3，5，7，9，11号座位的票，丁无法购买到第一排座位的票．若让丙第一购票，要使其他三人都能购买到第一排座位的票，写出满足条件的丁所选的座位号之和为____________．【答案】66．【分析】根据甲、乙、丙、丁四人购票，所购票数量分别为1，3，5，6可得若丙第一购票，要使其他三人都能购买到第一排座位的票，那么丙选座要尽可能得小，因此丙先选择：1，2，3，4，5．丁所购票数最多，即可得出丁应该为6，8，10，12，14，16，再将所有数相加即可．【详解】解：甲、乙、丙、丁四人购票，所购票数分别为1，3，5，6．∴丙选座要尽可能得小，选择：1，2，3，4，5．此时左边剩余5个座位，右边剩余6个座位，∴丁选：6，8，10，12，14，16．∴丁所选的座位号之和为681012141666+++++=；故答案为：66．【点睛】本题考查有理数的加法，认真审题，理解题意是解题的关键．12．我国古代的“河图”是由3×3的方格构成的，每个格内均有不同数目的数，每一行、每一列以及对角线上的三个数之和均相等．如图，给出了“河图”的部分数，则方格中左下角“△”代表的数是_____；方格中九个数的和是_____．【答案】-4 -27【分析】根据“河图”的特征可得：每一条对角线上的三个数的和等于第三行的各个数的和，求出△的值即可． 【详解】解：根据题意得：+(5)(3)(6)∆-=-+- 解得：=4∆-设与△和-3在同一条对角线上另一个数为y ，则有：(6)(5)(3)y +-=-+- ∴2y =-∴对角线上三个数的和为：(4)(3)(2)9-+-+-=-，即每一行，每一列以及线上三个数的和都等于-9， ∴方格中九个数的和是(9)(9)(9)27-+-+-=-， 故答案为：-4；-27【点睛】此题主要考查有理数的加法，图形的变化规律，学习过程中注意培养自己的观察、分析能力． 13．小颖同学做这样一道题“计算|5|-+∆”，其中“∆”是被墨水污染看不清的一个数，她翻开后面的答案，得知该题的计算结果是3，那么“∆”表示的数是_________． 【答案】2或8【分析】根据有理数的加法法则以及绝对值的性质解答即可； 【详解】∵53-+=△， ∴ 53-+=△或53-+=-△， 解得：=8或2， 故答案为：8或2．【点睛】本题考查了有理数的加法和绝对值的意义，熟记绝对值的意义是解答本题的关键；14．对于正数x 规定()1xf x x =+，例如133113(3),11343413f f ⎛⎫==== ⎪+⎝⎭+，计算1120152014f f ⎛⎫⎛⎫+ ⎪ ⎪⎝⎭⎝⎭111(1)(2)(3)(2013)(2014)(2015)201332f f f f f f f f f ⎛⎫⎛⎫⎛⎫++++++++++= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭__________．【答案】120142【分析】根据规定式子可得1111(),(1)1121111x f f x x x====+++，从而可得11()()111x f x f x x x+=+=++，由此即可得．【详解】因为对于正数x 规定()1xf x x=+，所以1111(),(1)1121111x f f x x x ====+++，所以11()()111x f x f x x x+=+=++， 则原式111(2015)(2014)(2)(1)201520142f f f f f f f ⎡⎤⎡⎤⎡⎤⎛⎫⎛⎫⎛⎫=+++++++⎪ ⎪ ⎪⎢⎥⎢⎥⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦⎣⎦⎣⎦， 1120142=⨯+， 120142=，故答案为：120142． 【点睛】本题考查了有理数加法运算的规律型问题，根据规定的运算式子，找出规律是解题关键．三、解答题15．10袋小麦称重后记录如图所示（单位：千克）．10袋小麦一共多少千克？如果每袋小麦以90千克为标准，10袋小麦总计超过多少千克或不足多少千克？【答案】10袋小麦一共905.4千克；10袋小麦总计超过5.4千克． 【分析】先求出10袋小麦90千克的增减量，然后相加即可得解．【详解】解：91+91+91.5+89+91.5+91.3+88.7+88.8+91.8+91.1=905.4（千克） 以90千克为标准，10袋小麦的记录如下：+1、+1、+1.5、-1、+1.2、+1.3、-1.3、-1.2、+1.8、+1.1，（+1）+（+1）+（+1.5）+（-1）+（+1.2）+（+1.3）+（-1.3）+（-1.2）+（+1.8）+（+1.1） =（+1）+（-1）+（+1.2）+（-1.2）+（+1.3）+（-1.3）+（+1）+（+1.5）+（+1.8）+（+1.1） =5.4千克．答：10袋小麦一共905.4千克；10袋小麦总计超过5.4千克．【点睛】本题考查了正负数的意义，读懂题目信息，写出90千克的增减量是解题的关键．16．某一出租车一天下午以鼓楼为出发地在东四方向营运，向东为正，向西为负，行车里程（单位：km ）依先后次序记录如下：9+，3-，8-，6+，6-，4-，10+．（1）将最后一名乘客送到目的地，出租车离鼓楼出发点多远？在鼓楼的什么方向？ （2）若每千米的价格为2.4元，司机一个下午的营运额是多少？ 【答案】（1）离鼓楼出发点为4km ，在鼓楼东；（2）110.4元【分析】（1）根据正数和负数意义，将所有的数相加所得结果即可得出答案；（2）根据绝对值的意义，将所有的数的绝对值相加即可得出总的路程，即可得出答案． 【详解】解：（1）由题意可得，+9+（-3）+（-8）+6+（-6）+（-4）+10=+4， 因为向东为正，向西为负，所以出租车离鼓楼出发点为4km ，在鼓楼东； （2）由题意可得，出租车营运的总路程为，|+9|+|-3|+|-8|+|6|+|-6|+|-4|+|10|=46（km ）， 营运额为：46×2.4=110.4（元）．【点睛】本题主要考查正负数的运算和绝对值的意义，根据题意列式计算是解决本题的关键．17．某食品厂计划平均每天生产200袋食品，但是由于种种原因，实际每天生产量与计划量相比有出入．下表是某周的生产情况（超过计划量记为正）：（1）根据记录的数据，求产量最多的一天比产量最少的一天多生产食品多少袋？ （2）根据记录的数据，求该厂本周实际共生产食品多少袋？ 【答案】（1）20；（2）1410．【分析】（1）根据题意和表格可以求得该厂产量最多的一天的产量和产量最少一天的产量，从而可以解答本题；（2）根据表格求出本周一共比计划多生产10袋，可求得该厂本周实际共生产食品多少袋． 【详解】解：（1）最多的一天为星期四：20011211+=（袋）， 最少的一天为星期五：2009191-=（袋），21119120-=（袋），产量最多的一天比产量最少的一天多生产食品多20袋；（2）5171195610+--+-++=（袋） 2007101410⨯+=（袋） 答：该厂本周实际共生产食品1410袋．【点睛】本题考查正数和负数的意义和有理数加法，解题的关键是明确题意，准确列式计算．18．某公路检修小组早上从A 地出发，沿东西方向的公路上检修路面，晚上到达B 地，如果规定向东行驶为正，向西行驶为负，一天行驶记录如下（单位：千米）：﹣5，﹣3，+6，﹣7，+9，+8，+4，﹣2． （1）请你确定B 地位于A 地的什么方向，距离A 地多少千米？ （2）距A 地最远的距离是多少千米？（3）若每千米耗油0.2升，问这个小组从出发到收工共耗油多少升？【答案】（1）B 地在A 地的东边10千米；（2）最远处离出发点12千米；（3）8.8升【分析】（1）计算这些有理数的和，即可知道收工时，B 地位于A 地的什么方向，距A 地多远， （2）逐次计算结果，当达到绝对值最大时即可， （3）求出各个数的绝对值的和，进而求出用汽油的升数． 【详解】解：（1）∵﹣5﹣3+6﹣7+9+8+4﹣2＝10， 答：B 地在A 地的东边10千米；（2）∵路程记录中各点离出发点的距离分别为： |﹣5|＝5（千米）；|﹣5﹣3|＝8（千米）；|﹣5﹣3+6|＝2（千米）；|﹣5﹣3+6﹣7|＝9（千米）；|﹣5﹣3+6﹣7+9|＝0（千米）；|﹣5﹣3+6﹣7+9+8|＝8（千米）；|﹣5﹣3+6﹣7+9+8+4|＝12（千米）；|﹣5﹣3+6﹣7+9+8+4﹣2|＝10（千米）；12＞10＞9＞8＞5＞2＞0，∴最远处离出发点12千米；（3）这一天走的总路程为：|﹣5|+|﹣3|+|+6|+|﹣7|+|+9|+|+8|+|+4|+|﹣2|＝44（千米），应耗油44×0.2＝8.8（升），答：问这个小组从出发到收工共耗油8.8升．【点睛】本题考查有理数的加法、绝对值的意义，理解有理数和绝对值的意义是正确解答的关键．19．如果自然数m使得作竖式加法m+（m+1）+（m+2）时对应的每一位都不产生进位现象，则称m为“三生三世数”，例如：12，321都是“三生三世数”，理由是12+13+14及321+322+323分别都不产生进位现象；50，123都不是“三生三世数“，理由是50+51+52及123+124+125分别产生了进位现象（1）分别判断42和3210是不是“三生三世数”，并说明理由；（2）求三位数中小于200且是3的倍数的“三生三世数”．【答案】（1）42不是“三生三世数”，3210是“三生三世数”，理由见解析；（2）102，111，120，132【分析】（1）根据“三生三世数”的定义进行判断便可；（2）先根据“三生三世数”定义求出三位数中小于200的“三生三世数”，再求得其中是3的倍数的数便可．【详解】解：（1）∵42+43+44计算时会产生进位现象，∴42不是“三生三世数”，∵3210+3211+3212计算时不会产生进位现象，∴3210是“三生三世数”，（2）根据“三生三世数”的定义知，小于200的三位数中的“三生三世数”有：100，101，102，110，111，112，120，121，122，130，131，132，∵102，111，120，132能被3整除，∴三位数中小于200且是3的倍数的“三生三世数”有：102，111，120，132．【点睛】本题考查了有理数的加法、新定义，解题的关键是明确题意，利用题干中的新定义解答． 20．从数轴上看： a 表示数a 的点到原点之间的距离，类似地4a -表示数a 的点到表示数4的点之间的距离．一般地a b -表示数a 的点到表示数b 的点之间的距离．（1）在数轴上，若表示数x 的点与表示数2-的点之间的距离为5个单位长度，则 x =________；． （2）对于任何有理数x ，式子 16x x ++- 有最_____（大或小）值，该值为________．（3）利用数轴，求方程 549x x -++= 的所有整数解的和.【答案】（1）3或-7；（2）小，7；（3）5【分析】（1）根据两点间的距离公式即可求解；（2）先得到16x x ++-的意义，再判断取值；（3）先得到549x x -++=的意义，从而得到相应的x 的范围，得到整数取值，最后相加．【详解】解：（1）∵表示数x 的点与表示数-2的点之间的距离为5个单位长度， ∴25x +=，解得：x =3或-7；（2）16x x ++-表示数轴上到-1和6的距离之和，∴有最小值，当x 在-1和6之间（包含-1和6）时，该值最小，且为7；（3）549x x -++=表示数轴上表示x 的数到-4和5的距离之和为9，则当x ＜-4或x ＞5时，549x x -++>，当-4≤x ≤5时，满足条件，此时x 的整数值为：-4，-3，-2，-1，0，1，2，3，4，5，∴所有整数解的和为-4-3-2-1+0+1+2+3+4+5=5．【点睛】本题考查了数轴，绝对值的性质，读懂题目信息，理解数轴上两点间的距离的表示是解题的关键．。

专题2.18 有理数的除法（拓展提高）一、单选题1．下列计算中，正确的是（ ）． A ．1515-=- B ．4.5 1.7 2.5 1.8 5.5--+=C ．()22--=D ．()1313-÷-=【答案】C【分析】根据绝对值、相反数、有理数加减和乘除运算的性质，对各个选项逐个分析，即可得到答案． 【详解】1515-=，故选项A 错误； 4.5 1.7 2.5 1.8 2.1--+=，故选项B 错误；()22--=，故选项C 正确；()111133339⎛⎫-÷-=-⨯-= ⎪⎝⎭，故选项D 错误； 故选：C ．【点睛】本题考查了绝对值、相反数、有理数运算的知识；解题的关键是熟练掌握绝对值、相反数、有理数加减和乘除运算的性质，从而完成求解．2．在数轴上有a 、b 两个有理数的对应点，则下列结论中，正确的是（ ）A ．0a b +>B ．0ab >C ．0a b -<D ．0ab> 【答案】C【分析】根据数轴上的位置判断a 、b 两个有理数的正负和绝对值大小即可． 【详解】解：根据数轴可知，a ＜0，b ＞0，a b >， ∴0a b +<，0ab <，0ab<，0a b -<， ∴A 、B 、D 错误，C 正确; 故选：C ．【点睛】本题考查了数轴上表示数和有理数的运算，解题关键是通过数轴确定两个有理数的正负和绝对值大小．3．已知数a b c ，，的大小关系如图所示，下列选项中正确的有（ ）个 ①0abc > ②0a b c +-> ③||1||||a b c a b c++= ④||||||2a b c a b c a --++-=-A ．0B ．1C ．2D ．3【答案】C【分析】根据数轴可以得到a<0，c>b>0，|c|>|a|>|b|，再根据有理数的乘除法法则，有理数的加法法则及绝对值的性质即可得出答案．【详解】解：由数轴可得a<0，c>b>0，|c|>|a|>|b|， ∴①0abc <，故①错误；②∵c>b ，∴b-c<0，∵a<0，∴0a b c +-<，故②错误； ③∵a<0，∴1a a =-，∵c>b>0，∴1b b =，1c c =，∴||1111||||a b c a b c++=-++=，故③正确；④∵a<0，b>0，∴a-b<0，∴|a-b|=b-a ，∵a<0，c>0，且|c|>|a|，∴c+a>0，∴|c+a|=c+a ，∵c>b>0，∴b-c<0，∴|b-c|=c-b ，∴||||||2a b c a b c b a c a c b a --++-=---+-=-，故④正确． ∴③④两个正确． 故选C ．【点睛】本题考查了利用数轴判断式子的正负，有理数的运算法则，绝对值的性质等知识．解题的关键是灵活运用所学知识解决问题． 4．下列说法正确的是（ ） A ．绝对值是本身的数都是正数 B ．单项式23x y 的次数是2C ．除以一个不为0的数，等于乘以这个数的相反数D ．3π是一个单项式【答案】D【分析】根据绝对值的意义、有理数的除法法则、单项式的定义进行判断即可． 【详解】解：A 选项，绝对值是本身的数是正数或0，故原说法错误；B 选项，单项式23x y 的次数是3，故原说法错误；C 选项，除以一个不为0的数，等于乘这个数的倒数，故原说法错误；D 选项，3π表示一个数，是一个单项式，故正确；故选：D ．【点睛】本题主要考查了绝对值、单项式的定义以及有理数的除法，熟记相关定义和法则是解答本题的关键．5．有一列数1a ，2a ，3a ，，n a ，从第二个数开始，每个数都等于1与它前面那个数的倒数的差，若14a =，则2020a 为（ ） A ．2- B ．4 C ．34D ．13-【答案】B【分析】根据题意分别求出121131144a a =-=-=，231411133a a =-=-=-，34111(3)4a a =-=--=，由此得到规律进行计算即可 【详解】∵14a =， ∴121131144a a =-=-=，231411133a a =-=-=-，34111(3)4a a =-=--=，，数列每3个数为一个周期循环， ∵202036731÷=，∴2020a 个数与第一个数相等，即2020a =4， 故选：B【点睛】此题考查数字的变化规律，有理数的减法法则，除法法则，解此题的关键是能从所给出的条件中找到数据变化的规律 6．a 是有理数，我们把22a-称为a 的“哈利数”．如：3的“哈利数”是223=-2-，2-的“哈利数”是212(2)2=--，已知13a =，2a 是1a 的“哈利数”，3a 是2a 的“哈利数”，4a 是3a 的“哈利数”，．．．，依此类推，则2010a =（ ） A ．12B ．2-C ．3D ．43【答案】B【分析】分别求出数列的前5个数得出该数列每4个数为一周期循环，而20104=5022÷，从而可得答案．【详解】解：∵13a =，()23452212422,,,3,142322232223a a a a ∴==-======-----∴该数列每4个数为一周期循环， ∵20104=5022÷，∴20102 2.a a ==- 故选：B ．【点睛】本题考查数字的变换规律，列代数式，同时考查有理数的加减运算，除法运算，根据题意得出该数列每4个数为一周期循环是关键．二、填空题7．定义一种新的运算：x *y =2x y x +，如：3*1=3213+⨯=53，则2*3=__________． 【答案】4【分析】把原式利用题中的新定义计算转换为有理数运算，即可得到结果． 【详解】解：根据题中的新定义得：2232*342+⨯==， 故答案为：4【点睛】此题考查了新定义运算和有理数的混合运算，弄清题中的新定义是解本题的关键． 8．已知：2|2|(1)a b +++取最小值，则aab b+=________． 【答案】4【分析】先根据绝对值的非负性、偶次方的非负性求出a 、b 的值，再代入求值即可得． 【详解】20a +≥，2(1)0b +≥，2120()b a +∴++≥，∴当2120,0()b a ++==时，212()b a +++取得最小值0，20,10a b ∴+=+=，解得2,1a b =-=-， 则()2122214a ab b +=-⨯-+=+-=-， 故答案为：4．【点睛】本题考查了绝对值的非负性、偶次方的非负性、有理数的乘除法与加法，熟练掌握绝对值与偶次方的非负性是解题关键．9．有时两数的和恰等于这两数的商，如()4242-+=-÷，42423333+=÷等．试写出另外1个这样的等式______． 【答案】993322-+=-÷． 【分析】根据两数的和恰等于这两数的商的要求，举出实例即可．【详解】解：993322-+=-÷，()()11-1-122+=÷． 故答案为：993322-+=-÷．【点睛】本题考查生活经验的积累问题，掌握两数的和恰等于这两数的商是解题关键．10．已知m 、n 为有理数，那么m n -可看成数轴上表示数m 和数n 的两点之间的距离．若有理数x 在数轴上的位置如图所示，则22x x +-型的值为________．【答案】1【分析】由数轴上表示x 的点的位置，得到x 小于-2，可得出x+2都小于0，利用绝对值的代数意义：负数的绝对值等于它的相反数化简，去括号合并即可得到结果． 【详解】解：由数轴上表示x 的点的位置,得到x<-2， ∴x+2<0， ∴22x x +-＝22x x ----=1，故答案为1．【点睛】本题考查了数轴，绝对值，熟练掌握绝对值的化简是解本题的关键．11．对于任意有理数a ，b ，c ，d ，规定一种运算：a a c d b b d c =-，例如5(3)51231217⨯--⨯=-=-．那么3234--=_________．【答案】6【分析】根据规定的运算进行列式，再根据有理数的运算法则进行计算即可． 【详解】()()323423126634-=⨯--⨯-=-=-．故答案为：6．【点睛】本题考查了新定义运算及有理数的混合运算，理解题意，掌握运算法则是解题的关键． 12．如图，有理数a 、b 、c 在数轴上的对应点的位置如图所示： 则下列结论：①a+b-c ＞0：②b-a ＜0：③bc-a ＜0：④|a|b |c|-+=1a |b|c．其中正确的是_______．【答案】②③．【分析】根据数轴，得到11b a c <-<<<，然后绝对值的意义进行化简，即可得到答案． 【详解】解：根据题意，则11b a c <-<<<，∴0a b c +-<，故①错误；0b a -<，故②正确； 0bc a -<，故③正确；1(1)13acb a b c-+=--+=，故④错误； 故答案为：②③．【点睛】本题考查了数轴的定义，绝对值的意义，解题的关键是掌握数轴的定义，正确得到11b a c <-<<<．13．一天，甲乙两人利用温差测试测量山峰的高度，甲在山顶测得的温度是-4℃，乙此时在山脚测得的温度是8℃．已知在该地区高度每增加100米，气温大约降低0.6℃，则这个山峰的高度大约是__________米． 【答案】2000【分析】先根据题意列出运算式子，再计算有理数的加减乘除运算即可得． 【详解】由题意得：()()840.6100840.6100--÷⨯=+÷⨯⎡⎤⎣⎦，120.6100=÷⨯，=⨯，20100=（米），2000故答案为：2000．【点睛】本题考查了有理数加减乘除运算的实际应用，依据题意，正确列出运算式子是解题关键．14．1930年，德国汉堡大学的学生考拉兹，曾经提出过这样一个数学猜想：对于每一个正整数，如果它是奇数，则对它乘3再加1；如果它是偶数，则对它除以2．如此循环，最终都能够得到1．这一猜想后来成为著名的“考拉兹猜想”，又称“奇偶归一猜想”．虽然这个结论在数学上还没有得到证明，但举例验证都是正确的，例如：取正整数5，最少经过下面5步运算可得1，即：如果正整数m最少经过6步运算可得到1，则m的值为__．【答案】10或64【分析】根据得数为1，可倒推出第5次计算后得数一定是2，第4次计算后得4，依此类推，直至倒退到第1次前的数即可．【详解】解：如图，利用倒推法可得：由第6次计算后得1，可得第5次计算后的得数一定是2，由第5次计算后得2，可得第4次计算后的得数一定是4，由第4次计算后得4，可得第3次计算后的得数是1或8，其中1不合题意，因此第3次计算后一定得8 由第3次计算后得8，可得第2次计算后的得数一定是16，由第2次计算后得16，可得第1次计算后的得数是5或32，由第1次计算后得5，可得原数为10，由第1次计算后32，可得原数为64，故答案为：10或64．【点睛】考查有理数的运算，掌握计算法则是正确计算的前提，理解题意是重中之重．三、解答题 15．计算 （1）77()8181-+-= （2）()015-- = （3）( 2.25)(80)-⨯+=（4）3217⎛⎫÷-⎪⎝⎭= 【答案】（1）0；（2）15；（3）-180；（4）-49【分析】（1）先化简绝对值，再根据有理数加法法则计算； （2）先将减法化为加法再计算； （3）根据乘法法则计算；（4）将除法化为乘法，再根据乘法法则计算． 【详解】（1）77()8181-+-=77()8181-+=0； （2）()015-- =0+15=15； （3）( 2.25)(80)-⨯+=-180； （4）3217⎛⎫÷-⎪⎝⎭=721()3⨯-=-49． 【点睛】此题考查有理数的加法法则、减法法则、乘法法则、除法法则，熟练掌握各计算法则是解题的关键．16．如图A 在数轴上所对应的数为2-．（1）点B 在点A 右边距A 点4个单位长度，求点B 所对应的数；（2）在（1）的条件下，点A 以每秒2个单位长度沿数轴向左运动，点B 以每秒3个单位长度沿数轴向右运动，当点A 运动到6-所在的点处时，求,A B 两点间距离． 【答案】（1）2；（2）14个单位长度【分析】（1）根据左减右加可求点B 所对应的数；（2）先根据时间=路程÷速度，求出运动时间，再根据列出=速度×时间求解即可．【详解】解：（1）-2+4=2．故点B所对应的数是2；（2）（-2+6）÷2=2（秒），2+2+（2+3）×2=14（个单位长度）．答：A，B两点间距离是14个单位长度．【点睛】本题考查了数轴，有理数的混合运算，解题的关键是理解题意，列出算式．17．某集团公司对所属甲．乙两分厂下半年经营情况记录（其中“+”表示盈利，“﹣”表示亏损，单位：亿元）如下表．（1）计算八月份乙厂比甲厂多亏损多少亿元？（2）分别计算下半年甲、乙两个工厂平均每月盈利或亏损多少亿元？【答案】（1）0.3亿元，（2）甲平均每月盈利0.4亿元，乙平均每月亏0.2亿元．【分析】（1）由表可得出乙厂亏0.7亿元，甲厂亏0.4亿元，由此可得出结果．（2）将甲乙两厂每个月的盈利相加即可得出结果．【详解】解：（1）由图可得出乙厂亏0.7亿元，甲厂亏0.4亿元，0.7-0.4=0.3（亿元）∴可得出乙比甲多亏0.3亿元．（2）甲：﹣0.2﹣0.4+0.5+0+1.2+1.3＝2.4亿元，2.4÷6=0.4（亿元）；乙：1.0﹣0.7﹣1.5+1.8﹣1.8+0＝﹣1.2亿元，-1.2÷6=-0.2（亿元）．∴甲平均每月盈利0.4亿元，乙平均每月亏0.2亿元．答：八月份乙厂比甲厂多亏损0.3亿元；甲平均每月盈利0.4亿元，乙平均每月亏0.2亿元【点睛】本题考查了正负数的意义和有理数的加减法，解题关键正确理解正负数的意义，准确进行计算．18．请你先认真阅读材料：计算12112 ()() 3031065 -÷-+-解：原式的倒数是21121-+()3106530⎛⎫-÷-⎪⎝⎭＝2112()(30)31065-+-⨯-＝23×（﹣30）﹣110×（﹣30）+16×（﹣30）﹣25×（﹣30）＝﹣20﹣（﹣3）+（﹣5）﹣（﹣12） ＝﹣20+3﹣5+12 ＝﹣10 故原式等于﹣110再根据你对所提供材料的理解，选择合适的方法计算：11322()()4261437-÷-+-． 【答案】114-． 【分析】根据题意，先计算出113224261437⎛⎫⎛⎫-÷-+- ⎪ ⎪⎝⎭⎝⎭的倒数132216143742⎛⎫⎛⎫-+-÷- ⎪ ⎪⎝⎭⎝⎭的结果，再算出原式结果即可．【详解】解：原式的倒数是：132216143742⎛⎫⎛⎫-+-÷- ⎪ ⎪⎝⎭⎝⎭()132********⎛⎫=-+-⨯- ⎪⎝⎭13224242424261437⎛⎫=-⨯-⨯+⨯-⨯ ⎪⎝⎭()792812=--+-14=-，故原式114=-． 【点睛】本题主要考查了有理数的除法，读懂题意，并能根据题意解答题目是解决问题的关键．19．设0a >，x ，y 为有理数，定义新运算：||a x a x =⨯※．如323|2|6=⨯=※，()414|1|a a -=⨯-※．（1）计算20210※和()20212-※的值．（2）若0y <，化简()23y -※．（3）请直接写出一组,,a x y 的具体值，说明()a x y a x a y +=+※※※不成立．【答案】（1）0；4042；(2)6y -；（3）1a =，2x =，3y =-（答案不唯一）【分析】(1)根据题意※表示前面的数与后面数的绝对值的积，直接代入数据求解计算；(2)有y<0，得到y 为负数，进而得到-3y 为正数，去绝对值后等于本身-3y ，再代入数据求解即可；(3)按照题意要求写一组具体的,,a x y 的值再验算即可．【详解】解：(1)根据题意得:202102021|0|0=⨯=※； ()202122021|2|4042-=⨯-=※；(2)因为0y <，所以30y ->，所以()()232|3|236y y y y -=⨯-=⨯-=-※；(3)由题意，当,,a x y 分别取1a =，2x =，3y =-时，此时()2311※※(-1)=1-=，而11※2※(-3)=2+3=5+，所以，()a x y a x a y +=+※※※不成立．【点睛】本题是新定义题型，按照题目中给定的运算要求和顺序进行求解即可．20．我们知道，正整数按照能否被2整除可以分成两类：正奇数和正偶数，小浩受此启发，按照一个正整数被3除的余数把正整数分成了三类：如果一个正整数被3除余数为1，则这个正整数属于A 类，例如1，4，7等；如果一个正整数被3除余数为2，则这个正整数属于B 类，例如2，5，8等；如果一个正整数被3整除，则这个正整数属于C 类，例如3，6，9等．（1）2020属于 类（填A ，B 或C ）；（2）①从A 类数中任取两个数，则它们的和属于 类（填A ，B 或C ）；②从A 类数中任意取出15个数，从B 类数中任意取出16个数，从C 类数中任意取出17个数，把它们都加起来，则最后的结果属于 类（填A ，B 或C ）；（3）从A 类数中任意取出m 个数，从B 类数中任意取出n 个数，把它们都加起来，若最后的结果属于C 类，则下列关于m ，n 的叙述中正确的是 （填序号）．①m +2n 属于C 类；②|m ﹣n |属于B 类；③m 属于A 类，n 属于C 类；④m ，n 属于同一类．【答案】（1）A；（2）①B；②B；（3）①④【分析】（1）计算2020÷3，根据计算结果即可求解；（2）①从A类数中任取两个数进行计算，即可求解；②从A类数中任意取出15个数，从B类数中任意取出16个数，从C类数中任意取出17个数，把它们的余数相加，再除以3，根据余数判断即可求解；（3）根据m，n的余数之和，举例，观察即可判断．【详解】解：（1）2020÷3＝673…1，所以2020被3除余数为1，属于A类；故答案为：A；（2）①从A类数中任取两个数，如：（1+4）÷3＝1…2，（4+7）÷3＝3…2，被3除余数为2，则它们的和属于B类；②从A类数中任意取出15个数，从B类数中任意取出16个数，从C类数中任意取出17个数，把它们的余数相加，得（15×1+16×2+17×0）＝47÷3＝15…2，∴余数为2，属于B类；故答案为：①B；②B；（3）从A类数中任意取出m个数，从B类数中任意取出n个数，余数之和为：m×1+n×2＝m+2n，∵最后的结果属于C类，∴m+2n能被3整除，即m+2n属于C类，①正确；②若m＝1，n＝1，则|m﹣n|＝0，不属于B类，②错误；③若m＝1，n＝1，③错误；④观察可发现若m+2n属于C类，m，n必须是同一类，④正确；综上，①④正确．故答案为：①④．【点睛】本题考查了新定义的应用和有理数的除法，解题的关键是熟练掌握新定义进行解答．。

独家文档原创文章，请勿搬运感谢支持第二节海陆的变迁知识能力1.(2018 广东深圳高峰学校期中)根据板块构造学说可推断出 ( )A.红海面积会扩大B.地中海面积会扩大C.板块碰撞会形成裂谷D.日本很少发生地震2.(2018 云南师大五华实验中学期中)下列事实中,可以作为大陆漂移说证据的是( )A.陆地主要分布在南半球B.世界陆地轮廓都比较破碎C.大西洋两岸陆地轮廓的相似性D.我国东部海域发现森林和河流的遗迹读下图,回答 3—4 题。

3.(2018 福建福安期中)甲、丙两大洲的轮廓和生物相似性的特征说明了( )A.大陆漂移说B.海底扩张说C.地质力学D.板块构造学说4.(2018 福建福安期中)丙大洲位于( )A.亚欧板块B.非洲板块C.太平洋板块D.美洲板块5.观察下图,依据大陆漂移说分析现在的大西洋( )A.最终将消失B.没有变化C.不断扩张D.不断缩小6.近些年地震频发,人们心有余悸,很多地区的人们都在学习防震知识,其中错误的是( )A.在家中,应选择浴室、厕所等空间避震B.在教室,应在老师的指挥下迅速用书包护住头部,躲在课桌底下C.地震时,不要乘坐电梯D.在野外,一定要躲在山脚下7.下列叙述,正确的是( )A.大陆漂移说是德国地球物理学家莫霍提出来的B.大陆漂移说认为板块交界处地壳不稳定C.板块构造学说认为板块内部地壳稳定D.板块构造学说认为大西洋在不断缩小“阿尔卑斯山脉——滑雪者的终极梦想”,人们总是这样形容这座欧洲雪山。

读图,完成8—9 题。

8.阿尔卑斯山脉的形成与板块运动密不可分,与阿尔卑斯山脉的形成密切相关的板块是( )A.亚欧板块与非洲板块B.亚欧板块与印度洋板块C.印度洋板块与美洲板块D.非洲板块与印度洋板块9.小明根据所学的板块知识,对阿尔卑斯山脉及其周围的地理事物进行了大胆猜测,下列观点错误的是( )A.地中海将会逐渐缩小B.非洲和欧洲将会连成一体C.地中海、阿尔卑斯山区多地震D.阿尔卑斯山脉将不再发生变化读六大板块示意图,回答 10—11 题。

专题2.16 有理数的乘法（拓展提高）一、单选题1．若a ，b 在数轴上的位置如图所示，则下列选项不正确的是（ ）A ．ab ＜0B ．|a |＞|b |C ．a +b ＞0D ．a ＜﹣b ＜b ＜﹣a【答案】C【分析】根据数轴上数的位置，确定数的正负与绝对值大小即可．【详解】解：由数轴可得，a ＜0＜b ，|a|＞|b|，则ab ＜0，|a|＞|b|，a+b ＜0，a ＜﹣b ＜b ＜﹣a ，错误的是C ．故选：C ．【点睛】本题考查了数轴上的数和有理数运算法则，解题关键是根据数轴判断a ，b 的符号合绝对值大小，再根据有理数运算法则判断式子是否正确．2．如果两个有理数的和等于零，那么这两个有理数的积是（ ）A ．负数B ．正数C ．非负数D ．非正数 【答案】D【分析】根据有理数的加法法则可得这两个数为一正一负，或同为0，再根据乘法法则得到这两个有理数的积是负数或0．【详解】如果两个有理数的和等于零，那么这两个有理数互为相反数，故这两个数为一正一负，或同为0，则这两个有理数的积是负数或0，故选：D ．【点睛】此题考查有理数的加法法则和乘法法则，熟记法则是解题的关键．3．对于任意有理数,a b ，定义一种新运算“⊕”，规则如下：a b ab a b ⊕=+-．例如：525252⊕=⨯+-，则3(2)⊕-的计算结果等于()A ．-7B ．-1C ．-11D ．-5 【答案】B【分析】根据新运算法则解答即可．【详解】解：()()3(2)32326321⊕-=⨯-+--=-++=-．故选：B ．【点睛】本题考查了有理数的运算，正确理解新运算法则、明确求解的方法是解题的关键．4．在整数集合{3,2,1,0,1,2,3,4,5,6}---中选取两个整数填入“6⨯=”的○内，使等式成立则正确选取后不同填入．．．．的方法有（ ） A ．2种B ．4种C ．6种D ．8种 【答案】C【分析】计算积为6的数，每个式子为两种．【详解】解：-3×（-2）=6，：-2×（-3）=6；2×3=6，3×2=6；1×6=6，6×1=6，共有6种，故选：C ．【点睛】本题考查了有理数的乘法，属于基础题，注意3个式子，6种方法5．若234a b ==，，且0ab <，那么+a b 的值为（ ）A ．5或1B ．-5或-1C ．5或-5D ．1或-1【答案】D【分析】先根据题意确定a ，b 的所有可能取值，然后代入求值即可．【详解】解：∵234a b ==，∴a 3b 2=±=±，∵0ab <∴a 、b 异号当a=3，b=-2时 3-21a b +==当a=-3，b=2时321a b +=-+=-故选：D ．【点睛】此题主要考查求代数式的值，解题的关键是正确根据题意确定a ，b 的值．6．王叔叔将“绿色出行，从我做起”化为实际行动，坚持每天步行上下班，他以10000步为标准，超过的记作正数，不足的记作负数，记录了一周上下班的步数情况如下表，若王叔叔平均每步0.75米，请你计算本周（星期一至星期五）王叔叔上下班共步行了多少米（ ）A ．2500B ．10500C ．52500D ．39375【答案】D【分析】先根据题意和表格数字列出运算式子，再计算有理数的乘法与加减法即可得．【详解】由题意得：()1000051200800160050000.75⨯+-+++⨯⎡⎤⎣⎦， ()5000025000.75=+⨯，525000.75=⨯，39375=（米），即本周（星期一至星期五）王叔叔上下班共步行了39375米，故选：D ．【点睛】本题考查了正负数在实际生活中的应用、有理数乘法与加减法的应用，依据题意，正确列出运算式子是解题关键．二、填空题7．12021-的倒数的相反数是________． 【答案】2021【分析】直接利用倒数、互为相反数的定义分析得出答案．【详解】解：12021-的倒数为：-2021，则-2021的相反数是：2021． 故答案为：2021．【点睛】此题主要考查了倒数、相反数，正确把握相关定义是解题关键．8．乘积为240-的不同五个整数的平均值最大是__________．【答案】9【分析】显然是要使得负因数的绝对值尽量小，且正因数尽量大，符合的负因数只能为-1，然后正因数为1，2，3，40，再根据平均数的求法求出五个整数的平均值．【详解】解：∵要求乘积为-240的不同五个整数的最大平均值，又∵-1×1×2×3×40=-240， ∴平均值最大的五个因数为-1，1，2，3，40，∴五个整数的平均值为（-1+1+2+3+40）÷5=9．故答案为：9．【点睛】本题考查了有理数的乘法，本题确定负因数为-1是解题的关键．9．规定*是一种运算符号，且*2a b ab a =-，则计算()4*2*3-=_______．【答案】-16．【分析】按照新定义转化算式，然后计算即可．【详解】根据题意，2*3232(2)-=-⨯-⨯-=64-+=-2，()4*2*3-=()4*24(2)24-=⨯--⨯=88--=-16故答案为：-16．【点睛】本题考查了新定义运算，解题关键是把新定义运算转化为有理数计算，并准确计算．10．已知21x y -=-，且,a b 互为倒数，那么620132x aby y -+-=______．【答案】2010【分析】利用倒数的性质得到ab ＝1，代入原式计算后，提取公因式变形，将2x−y ＝−1代入计算即可求出值．【详解】由题意得：2x−y ＝−1，ab ＝1，则原式＝6x−2y−y ＋2013＝3（2x−y ）＋2013＝−3＋2013＝2010．故答案为：2010．【点睛】此题考查了代数式求值，倒数，熟练掌握倒数的性质是解本题的关键．11．若a 与b 互为相反数，c 与d 互为倒数，e 是绝对值最小的数，则()325a b cd e +-+=______．【答案】-2【分析】根据已知求出a+b、cd、e的值，代入代数式即可求出答案．【详解】解：∵a与b互为相反数，c与d互为倒数，e为绝对值最小的数，∴a+b=0，cd=1，e=0，∴3（a+b）-2cd+5e=3×0-2+5×0=-2．故答案为：-2．【点睛】本题考查了有理数的混合运算，代数式求值，相反数，绝对值，倒数等知识点，解此题的关键是求出a+b、cd、e的值，此题是一道容易出错的题目，但题型较好．12．若定义一种新的运算“*”，规定有理数a*b＝3ab，如2*（﹣4）＝3×2×（﹣4）＝﹣24．则16*（﹣2*5）＝_____．【答案】﹣15【分析】根据a*b＝3ab，可以求得所求式子的值．【详解】解：∵a*b＝3ab，∴16*（﹣2*5）＝16*[3×（﹣2）×5]＝16*（﹣30）＝3×16×（﹣30）＝﹣15，故答案为：﹣15．【点睛】本题考查有理数的混合运算、新运算，解答本题的关键是明确有理数混合运算的计算方法．13．某班级课后延时活动，组织全班50名同学进行报数游戏，规则如下：从第1位同学开始，序号为奇数的同学报自己序号的倒数加1，序号为偶数的同学报自己序号的倒数加1的和的相反数．如第1位同学报（111+），第2位同学报1(1)2-+，第3位同学报1(1)3+……这样得到的50个数的乘积为_______．【答案】-51【分析】先确定每位同学所报之数，再列算式，确定积的符号为负，再算积即可．【详解】解：第1位同学报（111+），第2位同学报1(1)2-+，第3位同学报1(1)3+，第4位同学报1(1)4-+，…，第49位同学报1(1)49+，第50位同学报1(1)50-+，列式得（111+）1(1)2⎡⎤⨯-+⎢⎥⎣⎦1(1)3⨯+1(1)4⎡⎤⨯-+⨯⨯⎢⎥⎣⎦1(1)49+1(1)50⎡⎤⨯-+⎢⎥⎣⎦， =21-32⨯43⨯54⨯⨯⨯50495150⨯， =51-．故答案为：-51．【点睛】本题考查有理数乘法与加法混合运算，掌握有理数混合运算法则，特别是负号的确定，多个有理数相乘，积的符号由负因数的个数决定，负因数有奇数个时，积为负，负因数有偶数个时，积为正是解题关键．14．已知a 是不等于1-的数，我们把11a +称为a 的和倒数．如：2的和倒数为11123=+，已知211,a a =是1a 的和倒数，3a 是2a 的和倒数，4a 是3a 的和倒数，…，依此类推，则31212a a a a ⋅⋯⋅=______． 【答案】1233【分析】根据和倒数的定义分别计算出a 1、a 2、a 3、…a 12的值，代入计算即可求解．【详解】解：a 1＝1，a 211112==+，a 3121312==+，413a 2513==+，515a 3815==+，618a 51318==+，7113a 821113==+，8121a 1334121==+，9134a 2155134==+，10155a 3489155==+，11189a 55144189==+，121144a 892331144==+， 则a 1•a 2•a 3…a 12＝1123581321345589144123581321345589144233233⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯=． 故答案为：1233【点睛】本题为新定义问题，理解和倒数的定义，并根据定义依次计算出a 1，a 2，a 3，a 4，a 5…a 12的值是解题关键．三、解答题15．计算（1）5116()()()6767+-+-+-； （2）（﹣20）﹣（﹣18）+（﹣14）﹣13；（3）111(8)()842-⨯-+； （4）（﹣8）×（﹣43）×（﹣0.125）×54． 【答案】（1）﹣13；（2）﹣29；（3）﹣3；（4）﹣53 【分析】（1）原式化简后，相加即可求出值；（2）原式利用减法法则变形，计算即可求出值；（3）原式利用乘法分配律计算即可求出值；（4）原式结合后，相乘即可求出值．【详解】解：(1)原式＝56﹣16﹣17﹣67＝23﹣1 ＝﹣13； （2）原式＝﹣20+18﹣14﹣13＝﹣47+18＝﹣29；（3）原式＝﹣8×18﹣8×（﹣14）﹣8×12 ＝﹣1+2﹣4＝﹣3；（4）原式＝﹣8×0.125×43×54 ＝﹣53． 【点睛】本题考查了有理数的混合运算，解题关键是熟练运用有理数运算法则和运算律进行计算． 16．若a ，b 互为相反数，c ，d 互为倒数，m 的绝对值是2，求a 234b m cd m++-的值． 【答案】1或-7【分析】根据a ，b 互为相反数，c ，d 互为倒数，m 的绝对值是2，可以求得a +b 、cd 、m 的值，从而可以求得所求式子的值．【详解】解：因为a ，b 互为相反数，c ，d 互为倒数，m 的绝对值是3，所以a +b ＝0，cd ＝1，m ＝±2．当m＝2时，a234bm cdm++-＝223142+⨯-⨯⨯＝0+4﹣3＝1；当m＝﹣2时，a234bm cdm++-＝()223142+⨯--⨯⨯＝0﹣4﹣3＝﹣7．所以a234bm cdm++-的值是1或-7．【点睛】本题考查了相反数的意义、倒数的意义、绝对值的意义、有理数的混合运算，明确相反数、倒数、绝对值的意义是解题关键．17．已知x，y为有理数，现规定一种新运算“*”，满足x*y＝xy﹣5例如：1*2＝1×2﹣5＝﹣3（1）请仿照上面的例题计算下列各题：①2*（﹣3）；②（4*5）*（﹣16）；（2）任意选择两个有理数，分别填入下列□和〇中，并比较它们的运算结果；多次重复以上过程，你发现：□*〇〇*□（用“＞”“＜”或“＝”填空）．【答案】（1）①﹣11；②﹣152；（2）＝【分析】（1）①利用题中的新定义计算即可求出值；②利用题中的新定义计算即可求出值，先计算括号里面的再计算；（2）设□和〇的数字分别为有理数a，b，利用新定义，分别计算□*〇与〇*□，再比较大小即可．【详解】解：（1）①根据题中的新定义得：原式＝2×（﹣3）﹣5＝﹣6﹣5＝﹣11；②根据题中的新定义得：原式＝（4×5﹣5）*（﹣16）＝15*（﹣16）＝15×（﹣16）﹣5＝﹣52﹣5＝﹣152；（2）设□和〇的数字分别为有理数a ，b ，根据题意得：a*b ＝ab ﹣5，b*a ＝ab ﹣5，即a*b ＝b*a ，则□*〇＝〇*□．故答案为：＝．【点睛】此题考查了有理数的混合运算，熟练掌握运算法则是解本题的关键．18．利用运算律计算有时可以简便例1：256172651782214-+-+=--++=-+=；例2：()99999910019900999801⨯=-=-=．请你参考黑板中老师的讲解，用运算律简便计算．（1）1112322+--； （2）计算：()221546463737-⨯-⨯+⨯--⨯． 【答案】（1）-3；（2）-10【分析】（1）根据加法交换律与加法结合律计算；（2）根据乘法分配律、加法交换律与加法结合律计算 ． 【详解】（1）原式1113252322=--+=-+=- （2）()221546463737-⨯-⨯+⨯--⨯． ()212544663377=-⨯+⨯--⨯-⨯ 2125463377⎛⎫⎛⎫=-⨯+-⨯+ ⎪ ⎪⎝⎭⎝⎭4610=--=-【点睛】本题考查有理数的简便运算，熟练掌握有理数的运算律是解题关键．19．小明家想要从某商场购买洗衣机和烘干机各一台，现在分别从,A B 两个品牌中各选中一款洗衣机和一款烘干机，它们的单价如表1所示．目前该商场有促销活动，促销方案如表2所示．表1：洗衣机和烘干机单价表表2：商场促销方案你认为有哪几种购买方案？请通过计算为小明家选择支付总费用最低的购买方案．【答案】①购买A 品牌的洗衣机与烘干机各一台；②购买B 品牌的洗衣机与烘干机各一台；③购买A 品牌的洗衣机一台，购买B 品牌的烘干机一台；④购买A 品牌的烘干机一台；购买B 品牌的洗衣机一台；方案①的总费用为13272元，方案②的总费用为12820元，方案③的总费用为12872元，方案④的总费用为14020元，总费用最低的方案为方案②．【分析】由表1可得购买方案有四种，再根据表2的优惠方案分别计算四种方案的购买费用，通过比较从而可得答案．【详解】解：由题意可得购买方案为：①购买A 品牌的洗衣机与烘干机各一台；②购买B 品牌的洗衣机与烘干机各一台；③购买A 品牌的洗衣机一台，购买B 品牌的烘干机一台；④购买A 品牌的烘干机一台；购买B 品牌的洗衣机一台；所以一共有四种方案．方案①：()70000.8113%110000.8400⨯⨯-+⨯-4872880040013272=+-=（元）方案②：()75000.8113%100000.8400⨯⨯-+⨯-5220800040012820=+-=（元）方案③：()70000.8113%100000.8⨯⨯-+⨯4872800012872=+=（元）方案④：()75000.8113%110000.8⨯⨯-+⨯5220880014020=+=（元）由12820＜12872＜13272＜14020,所以选择方案②购买B 品牌的洗衣机与烘干机各一台总费用最低．【点睛】本题考查的是有理数的混合运算的实际应用，数学分类思想的应用，掌握分类讨论数学思想是解题的关键．20．学习有理数的乘法后，老师给同学们这样一道题目：计算：2449(5)25⨯-，看谁算的又快又对，有两位同学的解法如下： 小明：原式＝12491249452492555-⨯=-=-； 小军：原式＝24244(49)(5)49(5)(5)24925255+⨯-=⨯-+⨯-=-； （1）对于以上两种解法，你认为谁的解法较好？（2）受上面解法对你的启发，你认为还有更好的方法吗？如果有，请把它写出来；（3）用你认为最合适的方法计算：1599(8)16⨯-． 【答案】（1）小军的解法较好；（2）还有更好的解法；解法见详解；（3）见详解；【分析】（1）根据计算判断小军的解法较好；（2）把244925写成15025⎛⎫- ⎪⎝⎭，然后利用乘法分配律进行计算即可得解； （3）把151916写成12016⎛⎫- ⎪⎝⎭，然后利用乘法分配律进行计算即可得解； 【详解】（1）小军的解法相对来说更简便一些，所以小军的解法较好；（2）还有更好的解法，()()()()241114495=505=5055=250=24925252555⎛⎫⨯--⨯-⨯--⨯--+- ⎪⎝⎭ ； （3）()()()()151111198=208=2088=160=159********⎛⎫⨯--⨯-⨯--⨯--+- ⎪⎝⎭ ； 【点睛】本题考查了有理数的乘法，主要是对乘法分配律的应用，把带分数进行适当的转化是解题的关键 ；。

专题1.2 认识分式（拓展提高）一、单选题1．已知分式2331x x -+的值为0，则（ ）A ．x ＝1B ．x ＝﹣1C ．x ＞1D ．x ＞﹣1【答案】A【分析】根据分式值为零的条件可得：3x 2﹣3＝0，且x +1≠0，再解即可． 【详解】解：由题可得，3x 2﹣3＝0，且x +1≠0， 解得x ＝±1，x ≠﹣1， ∴x ＝1， 故选：A ．【点睛】本题考查了分式值为零的条件，关键是掌握分式值为零的条件是分子等于零且分母不等于零．注意：“分母不为零”这个条件不能少． 2．要把分式2xyx y+的值扩大为原来的3倍，下面哪种方法是可行的（ ） A ．x 、y 的值都加上3B ．x 、y 的值都扩大为原来的3倍C ．x 的值不变、y 的值扩大为原来的3倍D ．x 的值扩大为原来的3倍、y 的值不变【答案】B【分析】根据分式的性质，逐一判断各个选项，即可得到答案． 【详解】解：A. x 、y 的值都加上3，分式2xyx y+的值不会扩大为原来的3倍 ，不符合题意； B. x 、y 的值都扩大为原来的3倍，分式2xyx y+的值扩大为原来的3倍，符合题意； C. x 的值不变、y 的值扩大为原来的3倍，分式2xyx y+的值不会扩大为原来的3倍 ，不符合题意； D. x 的值扩大为原来的3倍、y 的值不变，分式2xyx y+的值不会扩大为原来的3倍 ，不符合题意． 故选B ．【点睛】本题主要考查分式的基本性质，能够正确利用分式的性质变形是解题的关键． 3．已知11a x =+（0x ≠且1x ≠），2111a a =-，3211a a =-，……，111n n a a -=-，则2021a 等于（ ）A ．1x -+B ．1x +C ．1x x + D ．1x-【答案】D【分析】根据题中所给已知等式先求出前4个数，发现每3个数一个循环，进而可得则a 2021等于a 2的值．【详解】解：由于a 1=x +1（x ≠0或x ≠-1），所以21111a x x==---， 34111,1,?·····111111x xa a x x x x x +=====+++-+， 因为2021÷3=673······2， 所以a 2021=21a x=-．故选：D ．【点睛】本题考查了规律型：数字的变化类，解决本题的关键是观察数字的变化寻找规律． 4．已知两个不等于0的实数a 、b 满足0a b +=，则b aa b+等于（ ）A ．2-B ．1-C ．1D ．2【答案】A【分析】先化简式子，再利用配方法变形即可得出结果． 【详解】解：∵22=b a b a a b ab++，∴()2222==a b abb a b a a b ab ab+-++， ∵两个不等于0的实数a 、b 满足0a b +=，∴()22-2===-2a b ab b a ab a b ab ab +-+， 故选：A ．【点睛】本题考查分式的化简、配完全平方、灵活应用配方法是解题的关键． 5．下列分式中，属于最简分式的个数是（ ）①42x ，②221x x +，③211x x --，④11x x --，⑤22y x x y -+，⑥2222x y x y xy ++．A ．1个B ．2个C ．3个D ．4个【答案】B【分析】根据最简分式的定义判断即可．【详解】解：①422x x =，③21111x x x -=-+，④111x x -=--，⑤22y x y x x y-=-+，可约分，不是最简分式； ②221x x +，⑥2222x y x y xy ++分子分母没有公因式，是最简分式，一共有二个； 故选：B ．【点睛】本题考查了最简分式，解题关键是明确最简分式的定义，准确判断分子分母是否含有公因式．6．已知分式2x bx a-+（a，b为常数）满足下列表格中的信息：其中选项错误的是（）A．a＝1 B．b＝2 C．c＝43D．d＝3【答案】C【分析】将表格数据依次代入已知分式中，进行计算即可判断．【详解】解：A．根据表格数据可知：当x=-1时，分式无意义，即x+a=0，所以-1+a=0，解得a=1．所以A选项不符合题意；B．当x=1时，分式的值为0，即211b-=+，解得b=2，所以B选项不符合题意；C．当x=c时，分式的值为-1，即2211cc-=-+，解得c=13，所以C选项符合题意；D．当x=d时，分式的值为1，即2211dd-=+，解得d=3，所以D选项不符合题意．故选：C．【点睛】本题考查了分式的值、分式有意义的条件，解决本题的关键是掌握分式相关知识．二、填空题7．已知25ab=，则b ab a-+＝___．【答案】3 8【分析】由25ab=可得25a b=，设25a b==k，则a=2k，b=5k，然后代入b ab a-+求解即可．【详解】解：∵25 ab=∴25a b = 设25a b==k ，则a=2k ，b=5k ∴523538k k k k -=+．故填38．【点睛】本题主要考查了代数式求值，正确的对已知条件进行变形成为解答本题的关键．8．下列各式：15（1﹣x ），43x π-，222x y -，1x +x ，23x x ，其中是分式的有_____个．【答案】2【分析】看分母中是否含有字母，如果含有字母则是分式，如果不含有字母则不是分式．【详解】解：15（1﹣x ），43x π-，222x y -，分母中都不含字母，因此它们是整式，而不是分式．1x +x ，23x x，分母中含有字母，因此是分式． 分式有两个， 故答案为：2．【点睛】本题主要考查分式的定义，注意π不是字母，是常数，所以43xπ-，不是分式，是整式． 9．已知x ，y ，z 满足yz x =1，xz y =2，与xyz=3，则分式222xyz x y z ++的值为 ___． 【答案】611【分析】原分式的倒数为222x y z xyz xyz xyz++，根据分式的性质可化为x y z yz xz xy ++，把已知条件可化为11123x y z yz xz xy ===，，，代入即可得出x y z yz xz xy ++的值，再求出x y zyz xz xy ++值的倒数即可得出答案．【详解】解：原式的倒数为222222x y z x y z x y z xyz xyz xyz xyz yz xz xy++=++=++， ∵123yz xz xyx y z ===，，， ∴11123x y z yz xz xy ===，，， ∴11111236x y z yz xz xy ++=++=， ∴222611xyz x y z =++，故答案为：611． 【点睛】本题主要考查了分式的求值，熟练应用分式的性质进行合理变形是解决本题的关键．10．若分式222x x x ---的值为零，则x 的值为_______．【答案】1-【分析】根据分式的值为零的条件是分子为零而分母不为零，然后进行计算即可． 【详解】解：∵分式222x x x ---的值为零，∴220x x --=且20x -≠， 解方程得，11x =-，22x =；解不等式得，2x ≠， ∴1x =- 故答案为：1-．【点睛】本题考查了分式的值为零的条件和分式没有意义的条件，属于基础知识的考查，比较简单． 11．观察分析下列方程：①23x x +=；②65x x +=；③127x x+=．请利用它们所蕴含的规律，求关于x 的方程2254n nx n x ++=+-（n 为正整数）的根，你的答案是_____．【答案】x =n +4或x =n +5【分析】根据方程变形后，归纳总结得到一般性规律，求出所求方程的解即可． 【详解】解：123x x⨯+=，解得：2x =或1x =； 235x x⨯+=，解得：2x =或3x =； 347x x⨯+=，解得：3x =或4x =； 得到规律mnx m n x+=+，的解为：x m =或x n =； 所求方程整理得：()14214n n x n x +-+=+-，根据规律得：4x n -=或4+1x n -=， 解得：x =n +4或x =n +5 故答案为：x =n +4或x =n +5【点睛】此题考查了分式方程的解，弄清楚题中的规律是解本题的关键． 12．已知x 为整数，且2116224x x x x ++++--为整数，则所有符合条件的x 值的和为_____． 【答案】8【分析】先将原分式进行通分变形，约分化简，然后求得符合题意的解即可．【详解】解：2116224x x x x ++++-- ()()1162222x x x x x +=+++-+- ()()()()()()()()226222222x x x x x x x x x -++=+++-+-+-()()22622x x x x x -++++=+-()()3622x x x +=+-()()()3222x x x +=+-32x =-， ∵x ，32x -为整数 ∴23x -=，或23x -=-或21x -=-或21x -= ∴5x =或1x =-或1x =或3x = ∴()51318+-++=∴所有符合条件的x 值的和为：8． 故答案为：8．【点睛】本题主要考查分式的化简与分式的整数值，解此题的关键在于熟练掌握分式相关知识点． 13．已知实数m 、n 均不为0且22227m mn nm n mn--=-+，则11m n -=______．【答案】163【分析】将原分式化简得163n m mn -=，再两边同时除以mn 即可得结果． 【详解】由22227m mn nm n mn --=-+得24414m mn n m n mn --=-+所以163n m mn -=，则11163m n -= 故答案为：163【点睛】本题考查了分式的化简求值，观察式子得到已知与未知的式子之间的关系是解题的关键． 14．已知a 、b 、c 、d 、e 、f 都为正数，12 bcdef a =，14 acdef b =，18 abdef c =，2 abcef d =，4 abcdfe=，8 abcdef=，则222222a b c d e f +++++=________． 【答案】1198【分析】根据等式性质及分式性质进行计算即可求得结果．【详解】解：由12 bcdef a =，14 acdef b =，18 abdef c =，2 abcef d =，4 abcdfe=，8 abcde f =，可将每个等式的左右两边相乘得：()51abcdef abcdef=，∴1abcdef =， 2112bcdef a a a a ⋅==⋅，∴22a =，同理可得：24b =，28c =，212d =，214e =，218f =， ∴2222221198a b c d e f +++++=； 故答案为1198． 【点睛】本题主要考查等式性质及分式性质，熟练掌握等式性质及分式性质是解题的关键．三、解答题 15．通分： （1）x ab与ybc ； （2）2c bd 与234ac b； （3）(2)xa x 与(2)yb x ； （4）22()xyxy 与22xx y -． 【答案】（1）x cx ababc ，=y ay bc abc；（2）2284c bc bd b d ，223344acacdb b d；（3）(2)(2)x bxa x ab x ，(2)(2)yay b x ab x ；（4）2222222()()()xy x y xy x y x y x y ，2222()()x x xyx y x y x y【分析】（1）先确定x ab与ybc 的最简公分母是abc ，然后进行通分，即可解答本题． （2）先确定2c bd 与234acb的最简公分母是24b d ，然后进行通分，即可解答本题．（1）先确定(2)x a x 与(2)yb x 的最简公分母是(2)ab x ，然后进行通分，即可解答本题． （1）先确定22()xy xy 与22x x y-的最简公分母是2()()x y x y +-，然后进行通分，即可解答本题． 【详解】解：（1）x ab与y bc xab与ybc 的最简公分母是abc ， ∴x cxababc ，=y ay bc abc． （2）2c bd 与234ac b2cbd 与234acb的最简公分母是24b d ， ∴2284c bc bd b d ，223344acacdbb d． （3）(2)xa x 与(2)yb x(2)xa x 与(2)yb x 的最简公分母是(2)ab x ， ∴(2)(2)x bx a xab x ，(2)(2)yayb x ab x ． （4）22()xyxy 与22xx y -22()xy x y 与22x x y-的最简公分母是2()()x y x y +-， ∴2222222()22()()()()()xy xy x y x y xy x y x y x y x y x y ，22222()()()()()x x x y x xy x y x y x y x y x y ．【点睛】本题考查通分，解题的关键是找出它们的最简公分母． 16．已知2113x x =+，求241x x +的值． 【答案】17【分析】由2113x x =+可得0x ≠，再取倒数可得：213x x+=，即13x x +=，再求解原代数式的倒数242221112,x x x x x x +⎛⎫=+=+- ⎪⎝⎭从而可得答案. 【详解】解：由2113x x =+知0x ≠， 所以213x x+=，即13x x +=．所以2422221112327x x x x x x +⎛⎫=+=+-=-= ⎪⎝⎭．故241x x +的值为17．【点睛】本题考查的是利用倒数法求解分式的值，掌握222112x x x x ⎛⎫+=+- ⎪⎝⎭是解题的关键.17．先化简，再求值：2221121x x x x x x ⎛⎫ ⎪-÷⎭+⎝-++，然后从22x -<≤的范围内选取一个合适的整数作为x 的值代入求值． 【答案】1xx -，2 【分析】先运用分式的混合运算法则化简，然后再选择合适的x 代入求值即可．【详解】解：原式()()()222111x x x x x x x x +-+-=÷++ ()2111x x x x x -=÷++ ()2111x x x x x +=⨯+- 1xx =-． ∵22x -<≤且x 为整数, ∴1x =-，0，1，2， 要使分式有意义， ∴1x ≠-、0、1， ∴2x =， ∴原式2221==-． 【点睛】本题主要考查了分式的化简求值、分式有意义的条件，根据分式有意义的条件确定x 的值成为解答本题的关键．18．是否存在x 的值，使得当4a =时，分式22a xa x 的值为0？ 【答案】不存在x 的值，得当4a =时，分式22a xa x 的值为0 【分析】根据分式有意义与分式值为零的条件即可得出结论【详解】解：∵4a =时，40a x x ，4x =，2222440a x ，分式无意义，∴不存在x 的值，得当4a =时，分式22a xa x 的值为0． 【点睛】本题考查分式的值为零的条件，掌握分式的值为零的前提条件是分式有意义是解题关键．19．给定下面一列分式：3x y ，−52x y ，73x y ，−94x y ，…，（其中x ≠0）（1）把任意一个分式除以前面一个分式，你发现了什么规律？ （2）根据你发现的规律，试写出给定的那列分式中的第2013个分式． 【答案】（1）任意一个分式除以前面那个分式等于2x y -；（2）40272013x y．【分析】（1）利用分式的化简即可发现规律； （2）根据所发现的规律，求需要求的分式．【详解】解：（1）53773225942322;;;;x x x x x x yy x x y y y y y x y y ⎛⎫÷== ⎪⎛⎫-⎝⎭÷=---÷-⎪- ⎝⎭，规律是任意一个分式除以前面那个分式等于2x y-；（2）根据规律：后面一个分式除以前面那个分式等于2x y-，第一个分式是3x y ，所以第2013个分式应该是：20123240272013x x x y y y⎛⎫⨯-= ⎪⎝⎭． 【点睛】本题考查了分式的化简，解题的关键是：利用分式化简的法则计算找规律，然后运用规律求指定项的分式．20．观察下列式子，并探索它们的规律： 112122111111x x x x x x x x +-+-==+=+-----； 2322522552().11111x x x x x x x x -+-+-==+=+-+++++ （1）根据以上式子填空： ①3531x x +=++ ． ②ax ba x c+=++ ．（2）当x 取哪些正整数时，分式4321x x +-的值为整数？ 【答案】（1）①21x +；②b ac x c-+ ；（2）1或3 【分析】（1）观察可发现，原式子将分式化为“整式+分式”的形式，分别利用得出的规律化简即可； （2）利用所得规律化简原分式，再探究当x 取什么值时，4321x x +-的值为整数．即可得到答案． 【详解】解：（1）①3533+23322+3+11111x x x x x x x x +++===+++++． 故答案为21x +． ②+++ax b ax b ax b a x c x ac ac ac c x c ac b ac x c cx +++---===++++++ 故答案为b ac x c -+． （2）4342234255=22121212121x x x x x x x x +-++-=+=+----- 当x 为正整数，且21x -为5的约数时，4321x x +-的值为整数， 即21=1x -或21=5x -时，4321x x +-的值为整数． ∴1=1x ，2=3x ．即当x 为1或3时，4321x x +-的值为整数． 【点睛】本题考查规律型：分式的变化规律，分式的加减运算法则的逆用，解答本题的关键是根据所给式子找出规律，并利用规律解答．。

专题2.2认识三角形（拓展提高）一、单选题1．一个三角形的两边长分别为2和5，且第三边长为整数，这样的三角形的周长最大值是（）A．10 B．11 C．12 D．13【答案】D【分析】先根据三角形的三边关系定理求得第三边的取值范围；再根据第三边是整数，从而求得周长最大时，对应的第三边的长．【详解】解：设第三边为a，根据三角形的三边关系，得：5-2＜a＜5+2，即3＜a＜7，∵a为整数，∴a的最大值为6，则三角形的最大周长为6+2+5=13．故选：D．【点睛】此题考查了三角形的三边关系：三角形两边之和大于第三边，两边之差小于第三边．2．如图，在△ABC中，AB=5，AC=8，CD=3BD，点E是AC的中点，BE、AD交于点F，则四边形DCEF 的面积的最大值是（）．A．10cm2B．9cm2C．8cm2D．7cm2【答案】B【分析】连接CF，设S△BFD=a，根据CD=3BD，点E是AC的中点，得出S△CFD=3a，S△ABF=S△CBF=4a，S△ABD=5a，即可得出S△ADC=15a，S△AFC=12a，S△ABC=20a，进而得出S四边形DCEF=9a，从而得出S四边形DCEF=920S△ABC，当△ABC的面积取最大值时，四边形DCEF的面积的最大，求得△ABC的面积的最大值，即可求得结果．【详解】解：连接CF，设S △BFD =a ，∵CD =3BD ，∴S △CFD =3a ，S △ADC =3S △ABD ，∵点E 是AC 的中点，∴S △ABE =S △CBE ，S △AFE =S △CFE ，∴S △ABF =S △CBF =4a ，∴S △ABD =5a ，∴S △ADC =15a ，∴S △AFC =12a ，S △ABC =20a ，∴S △EFC =6a ，∴S 四边形DCEF =9a ，∴S 四边形DCEF =920S △ABC ， ∵在△ABC 中，AB =5，AC =8，∴S △ABC 的最大值为：12×5×8=20，∴四边形DCEF 的面积的最大值是9(cm 2)，故选：B ．【点睛】本题考查了三角形的面积，根据等高的三角形面积的比等于它们底的比，得出S 四边形DCEF =920S △ABC 是解题的关键．3．如图，直线a ∥b ，在Rt △ABC 中，点C 在直线a 上，若∠1＝58°，∠2＝24°，则∠B 的度数为（ ）A ．56°B ．34°C ．36°D ．24°【答案】A 【分析】利用平行线的性质，三角形的外角的性质求出∠A 即可解决问题． 【详解】解：如图，∵a ∥b ，∴∠1=∠3=58°，∵∠3=∠2+∠A ， ∴∠A =58°-24°=34°， ∵∠ACB =90°， ∴∠B =90°-34°=56°， 故选：A ．【点睛】本题考查平行线的性质，三角形的外角的性质，三角形的内角和定理等知识，解题的关键是熟练掌握基本知识．4．如图，ABC 面积为1，第一次操作：分别延长AB ，BC ，CA 至点1A ，1B ，1C ，使1A B AB =，1B C BC =，1C A CA =，顺次连接1A ，1B ，1C ，得到111A B C △，则111A B C △的面积是（ ）A ．4B ．7C ．10D ．13【答案】B 【分析】根据题意，连接A 1C ，得到11A BC ABC S S ∆∆==，则11122A B B A BC S S ∆∆==，然后同理可求112C B C S ∆=，12AAC S ∆=，即可得到答案． 【详解】解：连接A 1C ，如图∵AB =A 1B ，∴△ABC 与△A 1BC 的面积相等， ∵△ABC 面积为1， ∴11A BC S ∆=．∵BB 1=2BC ， ∴11122A B B A BC S S ∆∆==，同理可得，112C B C S ∆=，12AAC S ∆=， ∴11122217A B C S ∆=+++=； 故选：B ．【点睛】本题考查了三角形的面积，三角形的中线问题，此题属规律性题目，解答此题的关键是找出相邻两次操作之间三角形面积的关系，再根据此规律求解即可．5．如图，在△ABC 中，∠A ＝78°，∠EBD ＝∠EDB ，DF 平分∠EDC ，则∠BDF 的度数为（ ）A ．35°B ．39°C ．40°D ．45°【答案】B 【分析】设,BDF x EBD y ∠=∠=，利用外角性质求出2AED y ∠=，利用角平分线性质得到EDF CDF x y ∠=∠=+，根据三角形内角和定理得到180A ADE AED ∠+∠+∠=︒，即可求出答案． 【详解】解：设,BDF x EBD y ∠=∠=，∵∠EBD ＝∠EDB ， ∴2AED y ∠=，∵DF 平分∠EDC ，∴EDF CDF x y ∠=∠=+， ∴180(22)ADE x y ∠=︒-+，∵180A ADE AED ∠+∠+∠=︒，∠A ＝78°， ∴78180(22)2180x y y ︒+︒-++=︒， 解得39x =︒， 故选：B ．【点睛】此题考查三角形内角和定理，角平分线的性质定理，外角的性质，读懂图形理解各角之间的位置关系是解题的关键．6．如图，将一副三角尺按图中所示位置摆放，点F 在AC 上，其中90ACB ∠=︒，60ABC ∠=︒，90EFD ∠=︒，45DEF ∠=︒，//AB DE ，则AFD ∠的度数是（ ）A ．15︒B ．30C ．45︒D ．60︒【答案】A 【分析】设AB 与EF 交于点M ，根据//AB DE ，得到45AMF E ∠=∠=︒，再根据三角形的内角和定理求出结果．【详解】解：设AB 与EF 交于点M ， ∵//AB DE ， ∴45AMF E ∠=∠=︒，∵90ACB ∠=︒，60ABC ∠=︒， ∴30A ∠=︒， ∴1803045105AFM ∠=︒-︒-︒=︒, ∵90EFD ∠=︒,∴AFD ∠=15︒， 故选：A ．． 【点睛】此题考查平行线的性质，三角形的内角和定理，熟记平行线的性质并应用是解题的关键． 二、填空题7．如图，在ABC 中，80A ∠=︒，30C ∠=︒，将CDE △沿DE 折叠得到C DE '，则12∠+∠等于__________________度．【答案】50°．【分析】连接DG ，将∠ADG+∠AGD 作为一个整体，根据三角形内角和定理来求解．【详解】解：连接DG ，根据折叠的性质，得：30C C '==︒∠∠，()()()12180'180'180180301808050C ADG AGD C A ∠+∠=︒-∠-∠+∠=︒-∠-︒-∠=︒-︒-︒-︒=︒故答案为：50°．【点睛】本题考查折叠的性质和三角形的内角和定理，解题的关键是作出辅助线帮助求解，熟练掌握基本知识，属于中考常考题型．8．如图，在ABC 中，80A ∠=︒，高BE 和CH 的交点为O ，则∠BOC =______ 【答案】100︒【分析】由BE 、CF 是△AB C 的高可得90BHC AEB ∠=∠=︒，根据三角形内角和定理可得∠ABE 的度数，进而可求出∠BOH 的度数，根据平角的定义即可得答案．【详解】∵BE 和CH 为ABC 的高， ∴90BHC AEB ∠=∠=︒， ∵80A ∠=︒，∴在ABE △中，180180908010ABE AEB A ∠=︒-∠-∠=︒-︒-︒=︒，在BHO △中，180180901080BOH BHO HBO ∠=︒-∠-∠=︒-︒-︒=︒， ∴180********BOC BOH ∠=︒-∠=︒-︒=︒． 故答案为：100︒．【点睛】本题考查三角形内角和定理，任意三角形的内角和等于180°，熟练掌握三角形内角和定理是解题关键．9．如图，△ABC 中，∠BDC ＝90°，BE 、CE 分别平分∠ABD 和∠ACD ，BF 、CF 分别平分∠ABE 和∠ACE ，若∠A ＝40°，则∠F ＝__°．【答案】52.5．【分析】利用三角形内角和、角平分线的性质求出∠FBC+∠FCB的度数，问题即可解决．【详解】解：∵∠A＝40°，∴∠ABC+∠ACB＝180°﹣40°＝140°，∵∠BDC＝90°，∴∠DBC+∠DCB＝90°，∴∠ABD+∠ACD＝140°﹣90°＝50°，∵BE、CE分别平分∠ABD和∠ACD，BF、CF分别平分∠ABE和∠ACE，∴∠FBD+∠FCD＝34×50°＝37.5°，∴∠FBC+∠FCB＝37.5°+90°＝127.5°，∴∠F＝180°﹣127.5°＝52.5°，故答案为52.5．【点睛】本题考查三角形内角和定理，角平分线的定义等知识，关键是熟练掌握这些基本知识，这是基本的题型．10．如图，△ABC中，BE、CD分别平分∠ABC、∠ACB，并相交于点O，∠BOC＝140°，则∠A＝__°．【答案】100【分析】先根据BO平分∠ABC，CO平分∠ACB，可得∠ABC＝2∠1，∠ACB＝2∠2，再根据三角形内角和定理计算出∠1+∠2的度数，进而得到∠ABC+∠ACB，即可算出∠A的度数．【详解】解：如图，∵BO平分∠ABC，CO平分∠ACB，∴∠ABC＝2∠1，∠ACB＝2∠2，∵∠BOC＝140°，∴∠1+∠2＝180°﹣140°＝40°，∴∠ABC+∠ACB＝2×40°＝80°，∴∠A＝180°﹣80°＝100°，故答案为：100【点睛】本题考查了角的平分线及三角形内角和定理，熟练掌握角的平分线与三角形内角和定理是解题的关键．11．如图，矩形ABCD的对角线AC，BD相交于点O，∠AOB＝70°，则∠ACB的大小为____．【答案】35°【分析】根据矩形的性质和等腰三角形的性质求得∠BAO的度数，再根据直角三角形的两锐角互余求解即可．【详解】解：∵四边形ABCD是矩形，对角线AC，BD相交于点O，∴OA＝OB，∠ABC＝90°，又∵∠AOB＝70°，∴∠BAO＝∠ABO＝12（180°﹣70°）＝55°，∴∠ACB＝90°﹣∠BAO＝90°﹣55°＝35°．故答案为：35°．【点睛】本题考查矩形的性质、等腰三角形的性质、直角三角形的两锐角互余，熟练掌握矩形的性质和等腰三角形的性质是解答的关键．12．如图，∠CAD和∠CBD的平分线相交于点P．请写出∠C、∠D、∠P的数量关系____________．【答案】2∠P＝∠D+∠C【分析】根据三角形的外角性质、角平分线的定义得到12∠CAD+∠P＝12∠CBD+∠C，12∠CAD+∠D＝12∠CBD+∠P，两式相减整理即可．【详解】解：∵∠BF A＝∠P AC+∠P，∠BF A＝∠PBC+∠C，∴∠P AC+∠P＝∠PBC+∠C，∵∠CAD和∠CBD的平分线相交于点P，∴∠P AC=∠P AD＝12∠CAD，∠PBC=∠PBD＝12∠CBD，∴12∠CAD+∠P＝12∠CBD+∠C①，∵∠DEP＝∠P AD+∠D，∠DEP＝∠EBP+∠P，∴12∠CAD+∠D＝12∠CBD+∠P②，①﹣②，得∠P﹣∠D＝∠C﹣∠P，整理得，2∠P＝∠D+∠C，故答案为：2∠P＝∠D+∠C．【点睛】本题考查角平分线定义，三角形外角性质，以及等式的性质，掌握角平分线定义，三角形外角性质，以及等式的性质是解题关键．13．如图，点O是ABCD的对称中心，点E为BC边的中点，点F为AD边上的点，且13DF AD．若12,S S 分别表示AOE △和CDF 的面积，则1S 与2S 之间的等量关系是______．【答案】1234S S = 【分析】根据三角形性质可得S 1=14ABC S ， S 2=13ADC S ，根据平行四边形性质可得 ABC ADC S S =，然后可以得到解答． 【详解】解：如图，连结OC ，则A 、O 、C 三点在同一直线上，∵O 是AC 中点，E 是BC 中点，∴S 1=11112224AEC ABC ABC S S S =⨯=，∵DF =13AD ， ∴S 2=13ADC S ， ∴S 1：S 2=113434=：， 即1234S S =， 故答案为1234S S =． 【点睛】本题考查三角形与平行四边形的综合应用，熟练掌握三角形中线的性质及平行四边形的对称性是解题关键．14．下图是可调躺椅示意图（数据如图），AE 与BD 的交点为C ，且A ∠，B ，E ∠保持不变．为了舒适，需调整D ∠的大小，使110EFD ∠=︒，则图中D ∠应___________（填“增加”或“减少”）___________度．【答案】减少 10【分析】先通过作辅助线利用三角形外角的性质得到∠EDF 与∠D 、∠E 、∠DCE 之间的关系，进行计算即可判断．【详解】解：∵∠A +∠B =50°+60°=110°， ∴∠ACB =180°-110°=70°， ∴∠DCE =70°， 如图，连接CF 并延长，∴∠DFM =∠D +∠DCF =20°+∠DCF ，∠EFM =∠E +∠ECF =30°+∠ECF ，∴∠EFD =∠DFM +∠EFM =20°+∠DCF+30°+∠ECF=50°+∠DCE=50°+70°=120°，要使∠EFD =110°，则∠EFD 减少了10°，若只调整∠D 的大小，由∠EFD =∠DFM +∠EFM =∠D +∠DCF +∠E +∠ECF =∠D +∠E +∠ECD =∠D +30°+70°=∠ D +100°，因此应将∠D 减少10度；故答案为：①减少；②10．【点睛】本题考查了三角形外角的性质，同时涉及到了三角形的内角和与对顶角相等的知识；解决本题的关键是理解题意，读懂图形，找出图形中各角之间的关系以及牢记公式建立等式求出所需的角，本题蕴含了数形结合的思想方法． 三、解答题15．已知ABC 中，AD BC ⊥于点D ，AE 平分BAC ∠，过点A 作直线//GH BC ，且60GAB ∠=︒，40C ∠=︒．（1）求ABC 的外角CAF ∠的度数；（2）求DAE ∠的度数．【答案】（1）100°；（2）10°【分析】（1）根据平行线的性质、对顶角相等计算即可；（2）根据角平分线的定义得到∠BAE =40°，根据平行线的性质求出∠GAD =90°，结合图形计算，得到答案．【详解】解：（1）∵GH ∥BC ，∠C =40°，∴∠HAC =∠C =40°，∵∠F AH =∠GAB =60°，∴∠CAF =∠HAC +∠F AH =100°；（2）∵∠HAC =40°，∠GAB =60°， ∴∠BAC =80°，∵AE 平分∠BAC ， ∴∠BAE =40°，∵GH ∥BC ，AD ⊥BC ， ∴∠GAD =90°， ∴∠BAD =90°-60°=30°，∴∠DAE =∠BAE -∠BAD =10°．【点睛】本题考查的是三角形的外角性质、三角形内角和定理、角平分线的定义、平行线的性质，掌握三角形内角和定理、平行线的性质是解题的关键．16．如图，ABC 中，80,30,BAC C BP ∠=︒∠=︒平分ABC ∠，点D 为射线BP 上一动点．（1）连接AD ，若//AD BC ，求ADB ∠的度数；（2）连接DC ，若DC 所在的直线垂直于ABC 的一边，则所有满足条件的BDC ∠的度数为__________．【答案】（1）35°；（2）125°或25°或55°【分析】（1）根据三角形内角和得到∠ABC ，根据角平分线的定义得到∠ABP ，再利用平行线的性质得到∠ADB ；（2）分1D C AB ⊥，2D C AC ⊥，3D C BC ⊥三种情况分别求解．【详解】解：（1）∵80BAC ∠=︒，30C ∠=︒， ∴70ABC ∠=︒，∵BP 平分ABC ∠， ∴35ABP CBP ∠=∠=︒， ∵//AD BC ， ∴35ADB CBP ∠=∠=︒．（2）①当1D C AB ⊥时，延长1CD 至E ，90BEC ∠=︒，135ABD ∠=︒， ∴11125BDC BEC ABD ∠=∠+∠=︒， ②当2D C AC ⊥时，223090120BCD ACB ACD ∠=∠+∠=︒+︒=︒， ∴221801803512025BD C CBP BCD ∠=︒-∠-∠=︒-︒-︒=︒，③当3D C BC ⊥时，390BCD ∠=︒，35CBP ∠=︒， ∴33180180359055BD C CBP BCD ∠=︒-∠-∠=︒-︒-︒=︒．【点睛】本题考查了平行线的性质，角平分线的定义，三角形内角和，垂直的定义，解题的关键是灵活运用所学知识，同时分类讨论解决问题．17．给出三个多项式26,2,2A x x B x C x =-+=-=+．（1）计算：A B -；（2）计算：()B C A B ⋅⋅-；（3）分别比较A 与B 、A 与C 的大小，并说明理由；（4）若22x -<<时，A 、B 、C 能否作为同一个三角形的三边长？请说明理由．【答案】（1）24x +；（2）416x -；（3）A B >；A C >，理由见解析；（4）不能；证明见解析【分析】（1）计算A -B ，去括号，合并同类项即可；（2）将A ，B ，C 代入，利用整式的混合运算法则计算即可；（3）分别计算A -B 和A -C ，根据结果比较即可；（4）计算B +C ，将A 利用完全平方公式变形，比较B +C 和A 的结果可得．【详解】解：（1）()262A B x x x -=-+--262x x x =-+-+24x =+；（2）()B C A B ⋅⋅-()()()2224x x x =-++()()2244x x =-+416x =-；（3）A 与B ，2440A B x -=+≥>， ∴A B >，A 与C ，()262A C x x x -=-+-+262x x x =-+--224x x =-+()213x =-+， ∵10x -≥， ∴30A C -≥>， 故A C >；（4）不能作为同一个三角形的三边长，∵224x x -++==B +C ，221232364244A x x x ⎛⎫=-+=-+≥> ⎪⎝⎭， ∴B C A +<，故A 、B 、C 不能同时作为同一个三角形的三边长．【点睛】本题考查了整式的混合运算，三角形的三边关系，完全平方公式，平方差公式，解题的关键是掌握整式的大小比较方法的使用．18．如图，在ABC 中，90,BAC AD BC ∠=︒⊥于点,D AE 平分,50DAC B ∠∠=︒，求BAD ∠和AEC ∠的度数．【答案】∠BAD =40°，∠AEC =115°【分析】先由三角形内角和定理求出∠C 的度数，再由直角三角形的性质即可求出∠BAD 的度数；在△ADC 中，由∠ADC =90°，∠C =40°可得出∠DAC 的度数，再由角平分线的性质即可求出∠DAE 的度数，再由直角三角形的性质求出∠AED 的度数，由两角互补的性质即可得出∠AEC 的度数．【详解】解：在△ABC 中，∵∠BAC =90°，∠B =50°，∴∠C =90°-∠B =40°，∵AD ⊥BC 于点D ，∴∠BAD =90°-∠B =40°；在△ADC 中，∵∠ADC =90°，∠C =40°，∴∠DAC =90°-∠C =50°，∵AE 平分∠DAC ，∴∠DAE =12∠DAC =25°， 在△DAE 中，∵∠ADE =90°，∠DAE =25°，∴∠AED =90°-∠DAE =65°，∴∠AEC =180°-∠AED =180°-65°=115°．【点睛】本题考查的是三角形内角和定理、角平分线的性质及两角互补的性质，熟知三角形的内角和是180°是解答此题的关键．19．如图，将一张三角形纸片ABC 的一角折叠，使得点A 落在四边形BCDE 的外部A '的位置且A '与点C 在直线AB 的异侧，折痕为DE ，已知90C ∠=︒，30A ∠=︒．（1）求12∠-∠的度数；（2）若保持A DE '的一边与BC 平行，求ADE ∠的度数．【答案】（1）60°；（2）45°或30°【分析】（1）先求出∠B 的度数，在根据四边形内角和求出∠1+∠BFD 的度数，由∠BFD =∠A ′FE 和∠A ′的度数可求出答案．（2）分EA '∥BC 和DA '∥BC 两种情况讨论．当DA '∥BC 时，先求出∠A ′DA =90°，再根据折叠可得出∠ADE =45°；当EA '∥BC 时，根据平行线的性质求出∠2=∠ABC =60°，由（1）得出∠1=120°，再根据折叠可求出∠ADE 的度数．【详解】解：（1）由折叠可知，30A A '∠=∠=︒在A EF '△中，2180A A FE ''∠+∠+∠=︒2180150A AFE A FE ''∴∠=︒-∠-∠=︒-∠在ABC 中，18060B C A ∠=︒-∠-∠=︒在四边形BCDF 中，1360C B BFD ∠+∠+∠+∠=︒1360210C B BFD BFD ∴∠=︒-∠-∠-∠=︒-∠ 因为BFD A FE '∠=∠1221015060∴∠-∠=︒-︒=︒（2）①当//DA BC '时，90ADA ACB '∠=∠=︒ ADE 沿DE 折叠A DE ' 1452ADE A DE ADA ''∴∠=∠=∠=︒②当//EA BC '时，260ABC ∠=∠=︒由（1）知，1260∠-∠=︒，1260120∴∠=∠+︒=︒，ADE 沿DE 折叠A DE '()11801302ADE A DE ADA ''∴∠=∠=∠=︒-∠=︒综上，∠ADE 的度数为：45°或30°．【点睛】本题考查了翻折变换的性质，三角形的一个外角等于与它不相邻的两个内角的和，三角形的内角和等于180°，平行线的性质，属于综合题，但难度不大．熟记性质准确识图是解题的关键．20．先阅读下面的内容，再解答问题．（阅读）例题：求多项式2222613m mn n n ++-+的最小值．解；()()2222222226132694()(3)4m mn n n m mn nn n m n n ++-+=+++-++=++-+，∵22()0,(3)0m n n +≥-≥ ∴多项式2222613m mn n n ++-+的最小值是4．（解答问题）（1）请写出例题解答过程中因式分解运用的公式是____________；（2）已知a 、b 、c 是ABC 的三边，且满足2210841a b a b +=+-，求第三边c 的取值范围； （3）求多项式2224369x xy y y -+--+的最大值． 【答案】（1）完全平方公式；（2）1＜c ＜9；（3）18【分析】（1）根据完全平方公式解答；（2）利用完全平方公式把原式变形，根据偶次方的非负性分别求出a 、b ，根据三角形的三边关系计算，得到答案；（3）利用完全平方公式把原式变形，根据偶次方的非负性解答即可．【详解】解：（1）例题解答过程中因式分解运用的公式是完全平方公式， 故答案为：完全平方公式；（2）a 2+b 2=10a +8b -41，a 2-10a +25+b 2-8b +16=0，（a -5）2+（b -4）2=0．∵（a -5）2≥0，（b -4）2≥0，∴a -5=0，b -4=0，∴a =5，b =4，∴5-4＜c ＜5+4，即1＜c ＜9；（3）原式=2222426918x xy y y y --+---+ =()()222226918x xy y y y ---++++ =()()222318x y y +---+∵-2（x -y ）2≤0，-（y +3）2≤0，∴多项式2224369x xy y y -+--+的最大值是18． 【点睛】本题考查的是配方法的应用，掌握完全平方公式、偶次方的非负性是解题的关键．。

专题1.8 同底数幂的除法（拓展提高）一、单选题1．下列计算正确的是（ ）A ．2223a a a +=B ．824a a a ÷=C ．324a a a ⋅=D ．()236a a = 【答案】D【分析】根据合并同类项法则，同底数幂的乘法和除法，幂的乘方运算法则对四个选项依次判断即可．【详解】解：A 选项，2223a a a +≠，故A 选项不符合题意；B 选项，8264a a a a ÷=≠，故B 选项不符合题意；C 选项，3254a a a a ⋅=≠，故C 选项不符合题意；D 选项，()236a a =，故D 选项符合题意． 故选：D ．【点睛】本题考查了合并同类项法则，同底数幂的乘法和除法，幂的乘方运算法则，熟练掌握这些知识点是解题关键．2．运算结果为6a 的式子是（ ）A ．32a a ⋅B ．()32aC ．122a a ÷D ．7a a -【答案】B【分析】先将选项中的式子进行化简算出正确的结果，然后进行对照即可解答本题．【详解】解：A .33522a a a a +⋅==，故不符合题意；B .()23236a a a ⨯==，符合题意；C .12210122=a a a a -=÷ ，故不符合题意；D . 7a 与a -无法合并，故不符合题意；故选：B【点睛】本题考查幂的乘方与积的乘方、合并同类项、同底数幂的乘除法，解题的关键是明确它们各自的计算方法．3．2a m =，3b m =，4c m =，则a b c m +-的值为．（ ）A ．1B ．1.5C ．2D ．2.5【答案】B【分析】根据幂的运算的逆运算，把所求变成同底数幂相乘和除法即可．【详解】解：=a a c b b c m m m m +-⨯÷，=234⨯÷=1.5故选：B ．【点睛】本题考查了幂的运算，解题关键是熟练运用幂的运算的逆运算，把所求式子变形．4．下列运算：①236a a a ⋅=；②()236a a =；③55a a a ÷=；④333()ab a b =．其中结果正确的有（ ） A ．1个B ．2个C ．3个D ．4个【答案】B 【分析】按照幂的运算法则直接判断即可．【详解】解：①235a a a ⋅=，原式错误；②()236a a =，原式正确； ③551a a ÷=，原式错误；④333()ab a b =，原式正确；故选：B ．【点睛】本题考查了幂的运算，熟记幂的运算法则，注意它们之间的区别是解题关键．5．太阳到地球的距离约为81.510km ⨯，光的速度约为53.010/km s ⨯，则太阳光到达地球的时间约为（ ） A ．50sB ．2510s ⨯C ．3510s ⨯D ．4510s ⨯ 【答案】B【分析】根据太阳到地球的距离除以光的速度，即可得出太阳光到达地球的时间．【详解】∵太阳到地球的距离约为1.5×108km ，光的速度约为3.0×105km/s ， ∴太阳光到达地球的时约为：（1.5×108）÷（3.0×105）=5×102（s ）．故选：B ．【点睛】本题主要考查了同底数幂的除法以及科学记数法，熟记幂的运算法则是解答本题的关键． 6．若33333333333m k +++⋅⋅⋅+=个（1k >，k ，m 都为正整数），则m 的最小值为（ ） A ．3B ．4C ．6D ．9 【答案】B【分析】计算3333333333333m k k +++⋅⋅⋅+=⋅=个，再利用同底数幂的除法，结合1k >，k ，m 都为正整数求得m的最小值．【详解】∵3333333333333mk k +++⋅⋅⋅+=⋅=个∴33m k -=．∵1k >，k ，m 都为正整数，∴k 的最小值为3，此时m 取得的最小值为4，故选B ．【点睛】本题考查同底数幂的除法．关键在于找到k 与m 之间的关系．二、填空题7．计算423287x y x y -÷的结果等于___________．【答案】4xy -【分析】利用同底数除法的法则计算即可【详解】解：423287x y x y -÷=-4x 4-3y 2-1=-4xy故答案为：-4xy【点睛】本题考查同底数除法法则，正确使用法则是关键8．已知9a =8，3b =4，则32a -b =__________；【答案】2【分析】根据幂的乘方法则以及同底数幂的除法法则计算即可．【详解】∵9a =（3a ）2=8，3b =4，∴32a -b =（3a ）2÷3b =8÷4=2，故答案为：2【点睛】本题主要考查了幂的运算，熟练掌握幂的运算法则是解答本题的关键．9．若x ，y 均为实数，432021x =，472021y =，则4347xy xy ⋅=______x y +；11x y+=_______． 【答案】2021 1【分析】根据同底数幂乘法、积的乘方、幂的乘方等计算法则进行等量代换即可．【详解】解：∵432021x =，472021y =∴(432021)x y y =，(472021)y x x =，4347(43)(47)202120212021xy xy x y y x y x x y +⋅=⨯=⨯=，故答案为：2021；∵=4)3(4347202147xy xy xy xy =⋅⨯，即20212021xy x y +=，∴xy x y =+， ∴111x y x y xy++==， 故答案为：1．【点睛】本题主要考查同底数幂乘法、积的乘方、幂的乘方等知识点，熟练掌握以上知识点的运算法则是解决本题的关键．10．已知8m a =，2n a =．则m n a -=___________，m 与n 的数量关系为__________．【答案】4 3m n =【分析】由同底数的除法可得：m n m n a a a -=÷，从而可得：m n a -的值，由2n a =，可得38,n a =可得3,m n a a =从而可得答案． 【详解】解：8m a =，2n a =∴ 824,m n m n a a a -=÷=÷=2n a =，()3328,n a ∴== 38,n a ∴=3,m n a a ∴=3.m n ∴=故答案为：43m n =，．【点睛】本题考查的是幂的乘方运算，同底数幂的除法运算，掌握以上知识是解题的关键．11．已知10m ＝20，10n 15=，则10m ﹣n ＝__；9m ÷32n =____ 【答案】100 81【分析】根据同底数幂的除法可得第一个空的值及m 与n 的关系，根据幂的乘方及同底数幂的除法即可得出第二个空的答案．【详解】解：∵10m ＝20，10n 15=， ∴10m ﹣n ＝10m ÷10n 1205=÷=100； ∴m ﹣n ＝2，9m ÷32n ＝32m ÷32n ＝32m ﹣2n ＝32（m ﹣n ）＝34＝81．故答案为：100；81．【点睛】本题考查了同底数幂的除法，根据法则计算是解题的关键．12．月球距离地球约为3.84×105千米，一架飞机速度约为8×102千米/时，若坐飞机飞行这么远的距离需__________天．【答案】20【分析】根据题意列出运算式子，再计算同底数幂的除法即可得．【详解】由题意得：()5224203.8410810⨯⨯÷÷=，即若坐飞机飞行这么远的距离需20天，故答案为：20．【点睛】本题考查了同底数幂除法的实际应用，依据题意，正确列出运算式子是解题关键．13．如果a c =b ，那么我们规定(a ，b)=c ，例如：因为23=8，所以(2，8)=3．若(3，5)=a ，(3，6)=b ，(3，m)=2a-b ，则m=________． 【答案】256【分析】由新规定的运算可得3a =5，3b =6，m=32a-b ，再将32a-b ，转化为2(3)3a b后，再代入求值即可． 【详解】解：由于(3，5)=a ，(3，6)=b ，(3，m)=2a-b ，根据新规定的运算可得，3a =5，3b =6，m=32a-b ， ∴222(3)5253366a a bb m -====， 故答案为：256． 【点睛】本题考查了幂的乘方，同底数幂的除法，掌握幂的乘方和同底数幂的除法的计算方法是正确计算的前提，理解新规定运算的意义是解决问题的关键．14．下列有四个结论．其中正确的是__．①若（x ﹣1）x +1＝1，则x 只能是2；②若（x ﹣1）（x 2+ax +1）的运算结果中不含x 2项，则a ＝1；③若a +b ＝10，ab ＝2，则a ﹣b ＝2；④若4x ＝a ，8y ＝b ，则23y ﹣2x 可表示b a． 【答案】②④【分析】根据多项式乘多项式、幂的乘方、同底数幂除法、零指数幂、完全平方公式等逐一进行计算即可．【详解】解：①若（x ﹣1）x +1＝1，则x 是2或﹣1．故①错误；②若（x ﹣1）（x 2+ax +1）的运算结果中不含x 2项，∵（x ﹣1）（x 2+ax +1）＝x 3+（a ﹣1）x 2+（1﹣a ）x ﹣1，∴a ﹣1＝0，解得a ＝1，故②正确；③若a +b ＝10，ab ＝2，∵（a ﹣b ）2＝（a +b ）2﹣4ab ＝100﹣8＝92，则a ﹣b ＝±③错误； ④若4x ＝a ，8y ＝b ，则23y ﹣2x ＝（23）y ÷（22）x ＝8y ÷4x ＝b a．故④正确． 所以其中正确的是②④．故答案为：②④．【点睛】本题考查多项式乘多项式、幂的乘方、同底数幂除法、零指数幂、完全平方公式等．熟练掌握相关公式是解题关键．三、解答题15．计算（1）23a a ⋅（2）()322y y ⋅ （3）3236415x y x y ⎛⎫-- ⎪⎝⎭ （4）852()()()x y y x y x -÷-⋅-．【答案】（1）5a ；（2）8y ；（3）64691125x y x y --；（4）5()y x - 【分析】（1）直接利用同底数幂的乘法计算即可；（2）先计算幂的乘方，再计算同底数幂的乘法；（3）直接利用积的乘方计算即可；（4）先利用乘方的符号法则将底数化为相同，再利用同底数幂的乘、除法计算即可．【详解】解：（1）原式=235a a +=；（2）原式=62y y ⋅=8y ；（3）原式=64691125x y x y --；（4）原式=852()()()y x y x y x -÷-⋅-=852()y x -+-=5()y x -．【点睛】本题考查幂的相关运算．主要考查同底数幂的乘、除法，幂的乘方和积的乘方．（4）中注意底数互为相反数时可先将底数化为相同在利用同底数幂的乘、除法计算．16．已知2m a =，3n a =．（1）求2m n a +的值；（2）23m n a -的值．【答案】（1）18；（2）427【分析】（1）先将2m n a +变形为()22=m n m n a a a a ，再代入m a ，n a 的值求解；（2）将23m n a -变形为()()23m n a a ÷，再代入m a ，n a 的值求解即可． 【详解】解：（1）原式2m n a a =()2=m n a a把2m a =，3n a =代入上式中 ()222318m n a a =⨯=（2）原式=23m n a a -()()23m n a a =÷ 把2m a =，3n a =代入上式中()()232342327m n a a ÷=÷= 故答案为：（1）18；（2）427． 【点睛】本题考查了同底数幂的除法、同底数幂的乘法，幂的乘方与积的乘方的知识，解答本题的关键在于熟练掌握各知识点的概念和运算法则．17．根据题意，完成下列问题．（1）若8,2322m n ==，求22m n -的值；（2）已知2330x y +-=，求48x y ⋅的值；（3）已知22332510x x x ++-⋅=，求x 的值．【答案】（1）2；（2）8；（3）52． 【分析】（1）先逆用同底数幂的乘法公式、同底数幂的除法公式和幂的乘方公式，将22m n -转化为()222m n ÷的形式，再代入8,2322m n ==进行计算即可；（2）先求出233x y +=，再利用幂的乘方公式和同底数幂的乘法公式将48x y ⋅转化为232x y +的形式，最后代入数值运算即可；（3）先逆用积的乘方公式将2225x x ++⋅转化为210x +，然后得到关于x 的一元一次方程后求解即可．【详解】解：（1）∵8,2322m n ==，∴()22222283264322m n m n -=÷=÷=÷=；∴22m n -的值为2．（2）∵2330x y +-=，∴233x y +=，∴232334822228x y x y x y +⋅=⋅===；∴48x y ⋅的值为8．（3）∵2222510x x x +++⋅=，∴2331010x x +-=，∴233x x +=-， ∴52x =， ∴x 的值为52． 【点睛】本题综合考察了同底数幂的乘法公式以及逆用、同底数幂的除法公式的逆用、幂的乘方公式及其逆用、积的乘方公式及其逆用等知识，要求学生能理解并熟记公式，能灵活运用公式对代数式进行变形等，考察了学生对基础知识的理解与公式的掌握，本题蕴含了整体代入的思想方法．18．（1）填空()10222-=()21222-=()32222-=（2）探索（1）中式子的规律，试写出第n 个等式，并说明理由．（3）计算234991*********+++++⋯++；【答案】（1）0， 1，2；（2）2n -2n -1=2n -1，理由见解析；（3）2101-1．【分析】（1）根据乘方的运算法则计算即可；（2）根据式子规律可得2n -2n -1=2n -1，然后利用提2n -1可以证明这个等式成立；（3）设题中的表达式为a ，再根据同底数幂的乘法得出2a 的表达式，相减即可．【详解】解：（1）21-20=2-1=20，22-21=4-2=21，23-22=8-4=22；故答案为： 0， 1，2；（2）第n 个等式为：2n -2n -1=2n -1，∵左边=2n -2n -1=2n -1（2-1）=2n -1，右边=2n -1，∴左边=右边，∴2n -2n -1=2n -1；（3）设a =20+21+22+23+…+299+2100．①则2a =21+22+23+…+299+2100+2101②由②-①得：a =2101-1∴20+21+22+23+…+298+2100=2101-1．【点睛】此题主要考查了探寻数列规律问题，认真观察、仔细思考，善用联想是解决这类问题的方法，注意观察总结规律，并能正确的应用规律，解答此题的关键是判断出：2n -2n -1=2n -1成立．19．小明和小红在计算100101133⎛⎫-⨯ ⎪⎝⎭时，分别采用了不同的解法． 小明的解法：10010010010110010011133333(1)33333⎡⎤⎛⎫⎛⎫⎛⎫-⨯=-⨯⨯=-⨯⨯=-⨯= ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦， 小红的解法：()100100100101101110110010111333333333--⎛⎫⎛⎫-⨯=⨯=⨯=⨯= ⎪ ⎪⎝⎭⎝⎭．请你借鉴小明和小红的解题思路，解决下列问题：（1）若4310a b -+=，求2213927a b +⨯÷的值；（2）已知x 满足24222296x x ++-=，求x 的值．【答案】（1）27；（2）32x =． 【分析】（1）根据同底数幂的乘法和除法化简2213927a b +⨯÷，然后再计算即可；（2）将24222296x x ++-=化成2222222926x x ++-=⨯，然后得到22232x +=，然后再化成指数相同计算即可．【详解】解：（1）2213927a b +⨯÷()()21223333a b+=⨯÷ 2423333a b +=⨯÷4433a b +-=4343a b -+=∵4310a b -+=∴431a b -=-∴原式1433327-+===；（2）∵24222296x x ++-=∴2222222926x x ++-=⨯∴()22222196x +-=⨯∴229326x +⨯=∴22232x +=∴22522x +=∴225x += ∴32x =． 【点睛】本题考查了同底数幂的运算，熟悉相关性质是解题的关键．20．阅读以下材料，苏格兰数学家纳皮尔（J ．Npler ，1550－1617年）是对数的创始人，他发明对数是在指数书写方式之前，直到18世纪瑞士数学家欧拉（Evler ．1707－1783年）才发现指数与对数之间的联系．对数的定义：一般地．若x a N =（0a >且1a ≠），那么x 叫做以a 为底N 的对数，记作log a x N =，比如指数式4216=可以转化为对数式24log 16=，对数式32log 9=可以转化为指数式239=．我们根据对数的定义可得到对数的一个性质：log ()log log (0,1,0,0)a a a M N M N a a M N ⋅=+>≠>>，理由如下：设log ,log a a M m N n ==，则,n m M a N a ==．m n m n M N a a a +∴⋅=⋅=．由对数的定义得log ()a m n M N +=⋅又log log a a m n M N +=+log ()log log a a a M N M N ∴⋅=+．根据上述材料，结合你所学的知识，解答下列问题：（1）填空：①2log 32=___________；②3log 27=_______，③7log l =________；（2）求证：log log log (0,1,0,0)a a a M M N a a M N N=->≠>>； （3）拓展运用：计算555log 125log 6log 30+-．【答案】（1）5，3，0；（2）见解析；（3）2【分析】（1）直接根据定义计算即可；（2）结合题干中的过程，同理根据同底数幂的除法即可证明；（3）根据公式：log a （M •N ）=log a M +log a N 和log a M N =log a M -log a N 的逆用，将所求式子表示为：5125630log ⨯，计算可得结论．【详解】解：（1）①∵5232=，∴2log 32=5，②∵3327=，∴3log 27=3，③∵071=，∴7log 1=0；（2）设log a M =m ，log a N =n ，∴m a M =，n a N =， ∴m n m n M a a a N -÷==， ∴log aM m n N =-， ∴log log log a a a M M N N=-； （3）555log 125log 6log 30+- =5125630log ⨯ =5log 25=2．【点睛】本题考查整式的混合运算、对数与指数之间的关系与相互转化的关系，解题的关键是明确新定义，明白指数与对数之间的关系与相互转化关系．。