锐角三角函数的定义

锐角三角函数是三角函数的一种，它们通过弧度制或角度制来定义，其中角度制是最常用的，用θ表示角度。

锐角三角函数是指在锐角和限制条件下的三角函数。

锐角三角函数的定义可以表示为：
sinθ=y/r，cosθ=x/r，tanθ=y/x，
其中，θ表示的是锐角的角度，r表示半径，x和y分别表示锐角的横轴和纵轴的长度。

锐角三角函数的定义是以弧度制和角度制为基础，用正弦、余弦和正切函数来表示，即sinθ、cosθ和tanθ，它们用来描述在锐角和限制条件下的三角函数。

在数学中，这些函数可以用来计算三角形的边长、角度等，是广泛应用的三角函数。

中考数学三角函数公式汇总与解析1.锐角三角函数锐角三角函数定义:锐角角A的正弦(si n),余弦(c o s)和正切(t a n),余切(c o t)以及正割(se c)，余割(c sc)都叫做角A的锐角三角函数。

正弦(si n)：对边比斜边，即si n A=a/c余弦(c o s)：邻边比斜边，即c o sA=b/c正切(t a n)：对边比邻边，即t a n A=a/b余切(c o t)：邻边比对边，即c o t A=b/a正割(se c)：斜边比邻边，即se c A=c/b余割(c sc)：斜边比对边，即c s c A=c/a2.3.互余角的关系s i n(π-α)=c o sα,c o s(π-α)=si nα,t a n(π-α)=c o tα,c o t(π-α)=t a nα.4.平方关系sin^2(α)+cos^2(α)=1tan^2(α)+1=sec^2(α)cot^2(α)+1=csc^2(α)5.积的关系s i nα=t a nα·c o sαc o sα=c o tα·si nαt a nα=si nα·se cαc o tα=c o sα·c s cαs e cα=t a nα·c scαc s cα=se cα·c o tα6.倒数关系t a nα·c o tα=1s i nα·c scα=1c o sα·se cα=17.诱导公式公式一：设α为任意角，终边相同的角的同一三角函数的值相等：s i n(2kπ+α)=si nαk∈zc o s(2kπ+α)=c o sαk∈zt a n(2kπ+α)=t a nαk∈zc o t(2kπ+α)=c o tαk∈z公式二：设α为任意角，π+α的三角函数值与α的三角函数值之间的关系：s i n(π+α)=-si nαc o s(π+α)=-c o sαt a n(π+α)=t a nα8.两角和差公式(1)si n(A+B)=si n A c o sB+c o sA si n B(2)si n(A-B)=si n A c o s B-si n B c o sA(3)c o s(A+B)=c o sA c o sB-si n A si n B(4)c o s(A-B)=c o sA c o sB+si n A si n B(5)t a n(A+B)=(t a n A+t a n B)/(1-t a n A t a n B)(6)t a n(A-B)=(t a n A-t a n B)/(1+t a n A t a n B)(7)c o t(A+B)=(c o t A c o t B-1)/(c o t B+c o t A)(8)c o t(A-B)=(c o t A c o t B+1)/(c o t B-c o t A)除了以上常考的三角函数公式外，掌握下面半角公式，积化和差和万能公式有利于快速解决选择题，达到事半功倍的效果哦！1.半角公式注：正负由α/2所在的象限决定。

中考复习：锐角三角函数知识梳理一、锐角三角函数（正弦、余弦、正切）1、定义：在Rt △ABC 中，∠C ＝90°，我们把锐角A的对边与斜边的比叫做∠A 的正弦（sinc ）， 记作sin A ，即sin A aA c∠==的对边斜边。

把∠A 的邻边与斜边的比叫做∠A 的余弦（cosine ），记作cos A ，即；把∠A 的对边与邻边的比叫做∠A 的正切（tangent ），记作tan A ，即。

锐角A 的正弦、余弦、正切都叫做∠A 的锐角三角函数（trigonometric function of acute angle ）。

当锐角A 的大小确定时，∠A 的对边与斜边的比（正弦）、∠A 的邻边与斜边的比（余弦）、∠A 的对边与邻边的比（正切）分别是确定的。

2、增减性：在0°到90°之间，正弦值、正切值随着角度的增大而增大，余弦随着角度的增大而减小。

3、取值范围：当∠A 为锐角时，三角函数的取值范围是：0＜sin A ＜1，0＜cos A ＜1，tan A ＞0。

4、互余两角的函数关系：如果两角互余，则其中一有的正弦等于另一角的余弦，即：若α是一个锐角，则sin α=cos （90°-α），cos α=sin （90°-α）。

5、正、余弦的平方关系：sin 2α+ cos 2α=1。

二、300、450、600的正弦值、余弦值和正切值如下表：三、解直角三角形bcos c A A ∠==的邻边斜边atan bA A A ∠=∠的对边＝的邻边C ∠A 的邻边b∠A 的对边a在直角三角形中，由已知元素求未知元素的过程就是解直角三角形。

1、在Rt△ABC 中，∠C＝90°，设三个内角A 、B 、C 所对的边分别为a 、b 、c （以下字母同），则解直角三角形的主要依据是：（1）边角之间的关系： sinA ＝cosB ＝a c ， cosA ＝sinB ＝bc，tanA ＝cotB ＝a b ，cotA ＝tanB ＝b a。

锐角三角函数基本概念三角函数是数学中的重要概念，用于描述角度与边长之间的关系。

锐角三角函数是指在单位圆上定义的三角函数，它们是我们在解决三角形相关问题时经常使用的基本工具。

本文将介绍锐角三角函数的基本概念，并探讨它们的性质和用法。

一、正弦函数（sin）正弦函数是最基本的锐角三角函数之一，它表示一个角的对边与斜边之比。

在单位圆上，设角A对应的点为P(x,y)，则正弦函数可以表示为：sinA = y正弦函数的定义域是所有锐角，值域是[-1,1]。

在解决三角形问题时，我们可以利用正弦函数来求解缺失的边长或角度。

二、余弦函数（cos）余弦函数是另一个重要的锐角三角函数，它表示一个角的邻边与斜边之比。

在单位圆上，设角A对应的点为P(x,y)，则余弦函数可以表示为：cosA = x与正弦函数类似，余弦函数的定义域是所有锐角，值域也是[-1,1]。

在实际问题中，我们可以通过余弦函数来计算未知边长或角度。

三、正切函数（tan）正切函数是通过正弦函数和余弦函数的比值而得到的，它表示一个角的对边与邻边之比。

在单位圆上，设角A对应的点为P(x,y)，则正切函数可以表示为：tanA = sinA / cosA = y / x正切函数的定义域是所有锐角，但值域却没有限制。

正切函数在解决问题时，常用于求解未知边长或角度。

四、割函数（sec）、余割函数（csc）和余切函数（cot）割函数（sec）、余割函数（csc）和余切函数（cot）是正弦函数、余弦函数和正切函数的倒数。

它们的定义如下：secA = 1 / cosA, cscA = 1 / sinA, cotA = 1 / tanA这三个函数在解决三角形问题时也经常使用，用于求解缺失的边长或角度。

五、三角恒等式锐角三角函数之间存在一些重要的恒等式，它们可以帮助我们简化计算或推导出其他有用的关系。

以下是一些常用的锐角三角函数恒等式：1. 余弦函数与正弦函数的平方和等于1：cos^2 A + sin^2 A = 12. 正切函数与割函数的乘积等于1：tanA · secA = 13. 正弦函数与余割函数的乘积等于1：sinA · cscA = 1除了这些基本的锐角三角函数，还有其他一些相关的三角函数，如反正弦函数、反余弦函数、反正切函数等。

锐角三角函数sin cos tan
我们要讨论锐角三角函数，包括正弦（sin）、余弦（cos）和正切（tan）。

首先，我们需要理解这些函数的基本定义和性质。

锐角三角函数是定义在锐角上的函数，这些函数与三角形的边和角有关。

1. 正弦（sin）: 正弦函数是定义为直角三角形中锐角的对边与斜边的比值。

2. 余弦（cos）: 余弦函数是定义为直角三角形中锐角的邻边与斜边的比值。

3. 正切（tan）: 正切函数是定义为直角三角形中锐角的对边与邻边的比值。

这些函数有一些重要的性质，例如：
1. 它们的值都在-1到1之间，这是因为在一个锐角三角形中，对边和邻边
的长度永远不会超过斜边的长度。

2. 正弦、余弦和正切函数在锐角范围内是单调的，这意味着随着角度的增加，它们的值也会增加。

3. 正弦和余弦函数在45度时相等（sin(45°) = cos(45°)），这是因为在一
个等腰直角三角形中，对边和邻边的长度是相等的。

4. 正切函数是无界的，这意味着随着角度的增加，正切函数的值可以无限增加或无限减少。

这些性质对于理解锐角三角函数非常重要，它们可以帮助我们解决各种与三角学相关的问题。

锐角三角函数作为数学中的一个重要概念，锐角三角函数是我们学习三角函数的关键部分之一。

在几何学和三角学中，锐角指的是小于90度的角。

而锐角三角函数是以锐角作为自变量的三角函数。

一、正弦函数（sine function）在锐角三角函数中，正弦函数是最常见也是最重要的一个函数。

正弦函数可以表示为：sin(θ) = 对边/斜边其中，θ代表锐角的度数，对边代表锐角的对边长度，斜边代表锐角的斜边长度。

二、余弦函数（cosine function）余弦函数是锐角三角函数中的另一个核心函数，表示为：cos(θ) = 临边/斜边同样，θ代表锐角的度数，临边代表锐角的临边长度，斜边代表锐角的斜边长度。

三、正切函数（tangent function）正切函数是另一个重要的锐角三角函数，表达式为：tan(θ) = 对边/临边在这个公式中，θ代表锐角的度数，对边代表锐角的对边长度，临边代表锐角的临边长度。

四、余切函数（cotangent function）余切函数是正切函数的倒数，可以表示为：cot(θ) = 临边/对边θ代表锐角的度数，临边代表锐角的临边长度，对边代表锐角的对边长度。

五、正割函数（secant function）正割函数是余弦函数的倒数，可以表示为：sec(θ) = 斜边/临边θ代表锐角的度数，斜边代表锐角的斜边长度，临边代表锐角的临边长度。

六、余割函数（cosecant function）余割函数是正弦函数的倒数，可以表示为：csc(θ) = 斜边/对边在这个公式中，θ代表锐角的度数，斜边代表锐角的斜边长度，对边代表锐角的对边长度。

锐角三角函数在数学和实际应用中具有广泛的重要性。

无论是在几何学、物理学还是工程学中，锐角三角函数都扮演着重要的角色。

它们可以帮助我们计算和解决各种三角形和锐角相关问题。

在实际应用中，锐角三角函数还广泛应用于测量和建模等领域。

总结起来，锐角三角函数是数学中不可或缺的一部分。

通过掌握和理解正弦函数、余弦函数、正切函数、余切函数、正割函数和余割函数，我们可以更好地理解和解决与锐角有关的各种数学和实际问题。

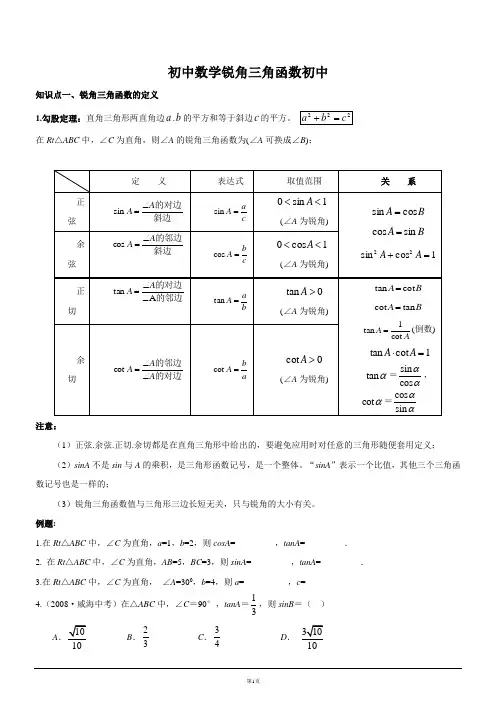
初中数学锐角三角函数初中知识点一、锐角三角函数的定义1.勾股定理：直角三角形两直角边a .b 的平方和等于斜边c 的平方。

222c b a =+ 在Rt △ABC 中，∠C 为直角，则∠A 的锐角三角函数为(∠A 可换成∠B )：定 义表达式 取值范围 关 系正弦 斜边的对边A A ∠=sin c aA =sin1sin 0<<A(∠A 为锐角)B A cos sin = B A sin cos =1cos sin 22=+A A余弦 斜边的邻边A A ∠=coscbA =cos1cos 0<<A(∠A 为锐角)正切的邻边的对边A tan ∠∠=A Aba A =tan 0tan >A(∠A 为锐角)B A cot tan = B A tan cot =AA cot 1tan =(倒数) 1cot tan =⋅A Atan α＝sin cos αα，cot α＝cos sin αα余切的对边的邻边A A A ∠∠=cotab A =cot 0cot >A(∠A 为锐角)注意：（1）正弦.余弦.正切.余切都是在直角三角形中给出的，要避免应用时对任意的三角形随便套用定义；（2）sinA 不是sin 与A 的乘积，是三角形函数记号，是一个整体。

“sinA ”表示一个比值，其他三个三角函数记号也是一样的；（3）锐角三角函数值与三角形三边长短无关，只与锐角的大小有关。

例题:1.在Rt △ABC 中，∠C 为直角，a =1，b =2，则cosA =________ ，tanA =_________．2. 在Rt △ABC 中，∠C 为直角，AB =5，BC =3，则sinA =________ ，tanA =_________．3.在Rt △ABC 中，∠C 为直角， ∠A =300，b =4，则a =__________，c =__________4.（2008·威海中考）在△ABC 中，∠C ＝90°，tanA ＝31，则sinB ＝（ ） A ．1010B ．23 C ．34D ．310105.在△ABC 中，∠C =90°，a, b, c 分别为∠A ，∠B ，∠C 的对边，下列各式错误的是（ ）A .a =c ·sinAB ．b =c ·cosBC ．b =a ·tanBD ．a =b ·tanA6.在△ABC 中，∠C ＝90°，(1)已知：c ＝ 83，∠A ＝60°，求∠B .a .b ． (2) 已知：a ＝36， ∠A ＝30°，求∠B .b .c .7.（2009·漳州中考）三角形在方格纸中的位置如图所示，则tan 的值是（ ）A ．35B ．43 C ．34D ．45练习:1.在Rt △ABC 中，∠C 为直角，若sinA =53，则cosB =_________． 2.已知cosA =23，且∠B =900-∠A ，则sinB =__________． 3.∠A 为锐角，已知sinA =135，那么cos (900-A)=___________ ． 4.在Rt △ABC 中，∠C 为直角，AC =4，BC =3，则sinA =（ ） A ．43 B ．34 C ． 53 D ．54 5.在Rt △ABC 中，∠C 为直角，sinA =22，则cosB 的值是( ) A ．21 B ．23 C ．1D ．22知识点二、特殊角所对的三角函数值1. 0°.30°.45°.60°.90°特殊角的三角函数值(重要)三角函数0° 30°45°60°90° αsin0 2122 231 αcos1 23 22210 αtan 0 331 3- αcot-3133注意：记忆特殊角的三角函数值，可用下述方法：0°.30°.45°.60°.90°的正弦值分别是02.12.22.32.42，而它们的余弦值分别是42.32.22.12.02；30°.45°.60°的正切值分别是13.22.31，而它们的余切值分别是31.22.13。

锐角三角函数介绍在三角函数中，我们经常会遇到锐角三角函数。

所谓锐角，是指小于90度的角度。

锐角三角函数包括正弦函数、余弦函数和正切函数。

正弦函数在数学中表示为sinθ，余弦函数表示为cosθ，正切函数表示为tanθ。

在本文中，我们将重点介绍锐角三角函数的定义、性质和常用公式。

正弦函数（sinθ）正弦函数是一个周期性函数，其定义域为实数集，值域为闭区间[-1, 1]。

数学上可以通过单位圆来理解正弦函数。

单位圆可以被看作是一个半径为1的圆，可以让我们更直观地理解正弦函数。

对于给定的角度θ，正弦函数的值等于单位圆上对应角度处点的y坐标。

正弦函数具有以下性质：1.正弦函数是一个奇函数，即sinθ = -sin(-θ)。

2.正弦函数在0度到90度之间是递增的，即sinθ在(0,90)区间内是单调递增的。

3.正弦函数在90度到180度之间是递减的，即sinθ在(90,180)区间内是单调递减的。

常用公式锐角三角函数有许多与角度相关的常用公式，下面是一些与正弦函数相关的常用公式：1.正弦函数的平方加上余弦函数的平方等于1，即sin^2(θ) + cos^2(θ) = 1。

2.正弦函数的和差公式：sin(α + β) = sinα·cosβ + cosα·sinβ。

3.正弦函数的二倍角公式：sin(2θ) = 2sinθ·cosθ。

4.正弦函数的半角公式：sin(θ/2) = ±√((1 - cosθ) / 2), 其中±表示与θ的象限有关的正负号。

余弦函数（cosθ）余弦函数也是一个周期性函数，其定义域为实数集，值域为闭区间[-1, 1]。

与正弦函数类似，我们可以通过单位圆来理解余弦函数。

对于给定的角度θ，余弦函数的值等于单位圆上对应角度处点的x坐标。

余弦函数具有以下性质：1.余弦函数是一个偶函数，即cosθ = cos(-θ)。

2.余弦函数在0度到90度之间是递减的，即cosθ在(0,90)区间内是单调递减的。

锐角三角函数1. 锐角三角函数的定义：如图所示：在Rt △ABC 中，∠C ＝90°，a ，b ，c 分别是∠A ，∠B ，∠C 的对边。

（1）∠A 的正弦：sinA ＝a cA ∠的对边＝斜边； （2）∠A 的余弦：b cA ∠的邻边＝斜边； （3）∠A 的正切：a bA A ∠∠的对边＝的邻边； （4）∠A 的余切：A b A a ∠∠的邻边＝的对边 （是正切的倒数）。

2.30°，45°，60°角的三角函数值：1sin 302︒=，2sin 452︒=，3sin 602︒=； 3cos302︒=，2cos 452︒=，1cos 602︒=； 3tan 303︒=，tan 451︒=，tan 603︒=。

例题1：求下列各式的值：（1）22cos 60sin 60︒+︒ （2）cos 45tan 45sin 45︒-︒︒3.锐角三角函数之间的关系：（1）平方的关系：22sin cos 1A A +=；（2）商的关系： sin tan cos A A A=; （3）互余两角的三角函数关系：sin(90)cos A A ︒-=，cos(90)sin A A ︒-=。

注意：锐角的正弦和正切值随着角度的增大而增大；锐角的余弦值随着角度的增大而减小；对于锐角A 有0sin 1,0cos 1,tan 0,A A A <<<<>且他们都没有单位。

4.直角三角形的有关性质及判定：（1）直角三角形的性质：①直角三角形两个锐角互余；②直角三角形斜边上的中线等于斜边的一半；③在直角三角形中，如果有一个锐角等于30︒，那么它所对的直角边等于斜边的一半；④在直角三角形中，如果有一条直角边等于斜边的一半，那么它所对的锐角等于30︒；⑤在直角三角形中，两条直角边a ，b 的平方和等于斜边c 的平方，即222a b c +=；⑥1122Rt S ch ab ==（h 为斜边上的高），外接圆半径R ＝2c ＝斜边上的中线，内切圆半径r ＝2a b c +-。

锐角三角函数—知识讲解【学习目标】1．结合图形理解记忆锐角三角函数定义；2．会推算30°、45°、60°角的三角函数值，并熟练准确的记住特殊角的三角函数值； 3．理解并能熟练运用“同角三角函数的关系”及“锐角三角函数值随角度变化的规律”.【要点梳理】要点一、锐角三角函数的概念如图所示，在Rt △ABC 中，∠C ＝90°，∠A 所对的边BC 记为a ，叫做∠A 的对边，也叫做∠B 的邻边，∠B 所对的边AC 记为b ，叫做∠B 的对边，也是∠A 的邻边，直角C 所对的边AB 记为c ，叫做斜边．锐角A 的对边与斜边的比叫做∠A 的正弦，记作sinA ，即sin A aA c ∠==的对边斜边；锐角A 的邻边与斜边的比叫做∠A 的余弦，记作cosA ，即cos A bA c ∠==的邻边斜边；锐角A 的对边与邻边的比叫做∠A 的正切，记作tanA ，即tan A aA A b∠==∠的对边的邻边.同理sin B b B c ∠==的对边斜边；cos B aB c∠==的邻边斜边；tan B b B B a ∠==∠的对边的邻边．要点诠释：(1)正弦、余弦、正切函数是在直角三角形中定义的，反映了直角三角形边与角的关系，是两条线段的比值．角的度数确定时，其比值不变，角的度数变化时，比值也随之变化． (2)sinA ，cosA ，tanA 分别是一个完整的数学符号，是一个整体，不能写成，，，不能理解成sin 与∠A ，cos 与∠A ，tan 与∠A 的乘积．书写时习惯上省略∠A 的角的记号“∠”，但对三个大写字母表示成的角(如∠AEF)，其正切应写成“tan ∠AEF ”，不能写成 “tanAEF ”；另外，、、常写成、、．(3)任何一个锐角都有相应的锐角三角函数值，不因这个角不在某个三角形中而不存在． (4)由锐角三角函数的定义知：当角度在0°<∠A<90°间变化时，，，tanA ＞0．要点二、特殊角的三角函数值Ca b c利用三角函数的定义，可求出30°、45°、60°角的各三角函数值，归纳如下：锐角30°45° 160°要点诠释：(1)通过该表可以方便地知道30°、45°、60°角的各三角函数值，它的另一个应用就是：如果知道了一个锐角的三角函数值，就可以求出这个锐角的度数，例如：若，则锐角．(2)仔细研究表中数值的规律会发现：、、的值依次为、、，而、、的值的顺序正好相反，、、的值依次增大，其变化规律可以总结为：①正弦、正切值随锐角度数的增大(或减小)而增大(或减小)；②余弦值随锐角度数的增大(或减小)而减小(或增大)．要点三、锐角三角函数之间的关系如图所示，在Rt△ABC中，∠C=90°．(1)互余关系：，；(2)平方关系：；(3)倒数关系：或；(4)商数关系：．要点诠释：锐角三角函数之间的关系式可由锐角三角函数的意义推导得出，常应用在三角函数的计算中，计算时巧用这些关系式可使运算简便．【典型例题】类型一、锐角三角函数值的求解策略1．如图所示，在Rt △ABC 中，∠C ＝90°，AB ＝13，BC ＝5，求∠A ，∠B 的正弦、余弦、正切值．【答案与解析】在Rt △ABC 中，∠C ＝90°． ∵ AB ＝13，BC ＝5． ∴ 222213512AC AB BC =-=-=．∴ 5sin 13BC A AB ==，12cos 13AC A AB ==，5tan 12BC A AC ==； 12sin 13AC B AB ==，5cos 13BC B AB ==，12tan 5AC B BC ==． 【总结升华】先运用勾股定理求出另一条直角边，再运用锐角三角函数的定义求值．举一反三：【变式】在Rt ΔABC 中，∠C =90°，若a =3，b =4，则c = ，sinA = ， cosA = ，sinB = ， cosB = ．【答案】c = 5 ，sinA = 35 ， cosA =45，sinB =45， cosB =35．类型二、特殊角的三角函数值的计算2．求下列各式的值：(1)（2015•茂名校级一模） 6tan 230°﹣sin60°﹣2sin45°； (2)（2015•乐陵市模拟） sin60°﹣4cos 230°+sin45°•tan60°； (3)（2015•宝山区一模） +tan60°﹣．【答案与解析】Ca bc解：（1）原式==122-．(2)原式=×﹣4×（）2+×=﹣3+=63-；(3)原式=+﹣=2+﹣=3﹣2+2=322+．【总结升华】熟记特殊角的三角函数值或借助两个三角板推算三角函数值，先代入特殊角的三角函数值，再进行化简．举一反三：【变式】在RtΔABC中，∠C=90°，若∠A=45°，则∠B=，sinA=，cosA=，sinB=，cosB=．【答案】∠B=45°，sinA=22，cosA=22，sinB=22，cosB=22．类型三、锐角三角函数之间的关系3．（2015•河北模拟）已知△ABC中的∠A与∠B满足（1﹣tanA）2+|sinB﹣|=0（1）试判断△ABC的形状．（2）求（1+sinA）2﹣2﹣（3+tanC）0的值．【答案与解析】解：（1）∵|1﹣tanA ）2+|sinB ﹣|=0，∴tanA=1，sinB=，∴∠A=45°，∠B=60°，∠C=180°﹣45°﹣60°=75°，∴△ABC 是锐角三角形；（2）∵∠A=45°，∠B=60°，∠C=180°﹣45°﹣60°=75°，∴原式=（1+）2﹣2﹣1=．【总结升华】本题考查的是特殊角的三角函数值，熟记各特殊角度的三角函数值是解答此题的关键．类型四、锐角三角函数的拓展探究与应用4．如图所示，AB 是⊙O 的直径，且AB ＝10，CD 是⊙O 的弦，AD 与BC 相交于点P ， 若弦CD ＝6，试求cos ∠APC 的值．【答案与解析】连结AC ，∵ AB 是⊙O 的直径，∴ ∠ACP ＝90°， 又∵ ∠B ＝∠D ，∠PAB ＝∠PCD ，∴ △PCD ∽△PAB ，∴PC CDPA AB=． 又∵ CD ＝6，AB ＝10， ∴ 在Rt △PAC 中，63cos 105PC CD APC PA AB ∠====．【总结升华】直角三角形中，锐角的三角函数等于两边的比值，当这个比值无法直接求解，可结合相似三角形的性质，利用对应线段成比例转换，间接地求出这个比值．锐角的三角函数是针对直角三角形而言的，故可连结AC ，由AB 是⊙O 的直径得∠ACB ＝90°，cos PC APC PA ∠=，PC 、PA 均为未知，而已知CD ＝6，AB ＝10，可考虑利用△PCD ∽△PAB 得PC CDPA AB=．(1)sad60°＝________．(2)对于0＜A ＜180°，∠A 的正对值sadA 的取值范围是_______．(3)如图1②，已知sinA ＝35，其中∠A 为锐角，试求sadA 的值．【答案与解析】(1)1； (2)0＜sadA ＜2；(3)如图2所示，延长AC 到D ，使AD ＝AB ，连接BD ．设AD ＝AB ＝5a ，由3sin 5BC A AB ==得BC ＝3a ， ∴ 22(5)(3)4AC a a a =-=，∴ CD ＝5a-4a ＝a ，22(3)10BD a a a =+=，∴ 10sadA 5BD AD ==． 【总结升华】(1)将60°角放在等腰三角形中，底边和腰相等，故sadA ＝1；(2)在图①中设想AB ＝AC的长固定，并固定AB 让AC 绕点A 旋转，当∠A 接近0°时，BC 接近0，则sadA 接近0但永远不会等于0，故sadA ＞0，当∠A 接近180°时，BC 接近2AB ，则sadA 接近2但小于2，故sadA ＜2；(3)将∠A 放到等腰三角形中，如图2所示，根据定义可求解．。

板块一 基础知识一、锐角三角函数的定义1. 锐角A 的正弦、余弦、正切、余切都叫做A ∠的锐角三角函数．2. 正弦：Rt ABC ∆中，锐角A 的对边与斜边的比叫做A ∠的正弦，记作sin A ，即sin aA c =． 3. 余弦：Rt ABC ∆中，锐角A 的邻边与斜边的比叫做A ∠的余弦，记作cos A ，即cos b A c =． 4. 正切：Rt ABC ∆中，锐角A 的对边与邻边的比叫做A ∠的正切，记作tan A ，即tan a A b =． 5. 余切：Rt ABC ∆中，锐角A 的邻边与对边的比叫做A ∠的余切，记作cot A ，即cot b A a=． 从定义中可以看出，① 正弦、余弦、正切、余切都是在直角三角形中给出的，要避免应用时对任意三角形随便套用定义． ② sin A 、cos A 、tan A 、cot A 分别是正弦、余弦、正切、余切的数学表达符号，是一个整体，不能理解为sin 与A 、cos 与A 、tan 与A 、cot 与A 的乘积．③ 在直角三角形中，正弦、余弦、正切、余切分别是某个锐角的对边与斜边、邻边与斜边、对边与邻边、邻边与对边的比值，当这个锐角确定后，这些比值都是固定值．二、特殊角三角函数这些特殊角的三角函数值一定要牢牢记住．三、锐角三角函数的取值范围在Rt ABC ∆中，90C ∠=︒，000a b c a c b c >>><<，，，，，又sin a A c =，cos b A c =，tan a A b =，cot bA a=，三角函数 0︒ 30︒45︒60︒90︒sin A 012 22 321cos A 132 22 12 0tan A 03313-cot A - 3 1 33三角函数所以0sin 10cos 1tan 0cot 0A A A A <<<<>>，，，．四、三角函数关系 1. 同角三角函数关系： 22sin cos 1A A +=，sin tan cos AA A=，tan cot 1A A ⋅= 2. 互余角三角函数关系：⑴ 任意锐角的正弦值等于它的余角的余弦值：()sin cos 90A A =︒-； ⑵ 任意锐角的余弦值等于它的余角的正弦值：()cos sin 90A A =︒-； ⑶ 任意锐角的正切值等于它的余角的余切值：()tan cot 90A A =︒-；⑷ 任意锐角的余切值等于它的余角的正切值：()cot tan 90A A =︒-． 3. 锐角三角函数值的变化规律：令1c =，锐角A ∠越小，则a 越小，则b 越大；当A ∠越大，则a 就越大，b 就越小，且a c b c <<，，所以当角度在0~90︒︒范围内变化时，正弦值随角度的增大（或减小）而增大（或减小）；余弦值随角度的增大（或减小）而减小（或增大）．而正切值也是随角度的增大（或减小）而增大（或减小）；余切值随角度的增大（或减小）而减小（或增大）．可以应用0~90︒︒间的正弦值、余弦值、正切值、余切值的增减性来比较角的正弦、余弦、正切、余切值的大小，其规律是：⑴A B 、为锐角且A B >，则sin sin A B >，cos cos A B <，tan tan A B >，cot cot A B <；⑵A B 、为锐角且A B <，则sin sin A B <，cos cos A B >，tan tan A B <，cot cot A B >．该规律反过来也成立．板块二 常用公式1. 和角公式：cos()cos cos sin sin αβαβαβ+=-，sin()sin cos cos sin αβαβαβ+=+，tan tan tan()1tan tan αβαβαβ++=-⋅；2. 差角公式：cos()cos cos sin sin αβαβαβ-=+，sin()sin cos cos sin αβαβαβ-=-，tan tan tan()1tan tan αβαβαβ--=+⋅；3. 倍角公式：2222cos2cos sin 2cos 112sin ααααα=-=-=-，sin22sin cos ααα=，22tan tan 21tan ααα=-； 4. 半角公式：21cos cos 22αα+=，21cos sin 22αα-=，sin 1cos tan 21cos sin ααααα-==+； 5. 万能公式：22tan2sin 1tan 2ααα=+，221tan 2cos 1tan 2ααα-=+，22tan2tan 1tan 2ααα=-；6. 积化和差公式：1cos cos [cos()cos()]2αβαβαβ=++-，1cos sin [sin()sin()]2αβαβαβ=+--，1sin cos [sin()sin()]2αβαβαβ=++-，1sin sin [cos()cos()]2αβαβαβ=-+--．7. 和差化积公式：cos cos 2cos cos22αβαβαβ+-+=，cos cos 2sin sin22αβαβαβ+--=-，sin sin 2sin cos22αβαβαβ+-+=，sin sin 2cossin22αβαβαβ+--=．板块一、三角函数基础【例1】 已知如图：在Rt ABC ∆中，810BC AC ==，.求sin A 和sin B 的值。

B知识点1 锐角三角函数1.定义：在Rt△ABC中，∠C=900,∠A、∠B、∠C的对边分别为a、b、c，则∠A的正弦可表示为：sinA= ，∠A的余弦可表示为cosA=∠A的正切：tanA= ，它们统称为∠A的锐角三角函数【名师提醒：1、sinA、∠cosA、tanA表示的是一个整体，是两条线段的比，没有单位，这些比值只与有关，与直角三角形的______无关;(2)正弦是角对边比斜边；余弦是邻边比斜边；正切是角的对边比邻边。

】2.特殊角的三角函数值【名师提醒：1、三个特殊角的三角函数值都是根据定义应用直角三角形性质算出来的，要在理解的基础上结合表格进行记忆2、正弦和正切值随着角度的增大而余弦值随着角度的增大而3、几个特殊关系：⑴sinA+cos2A= ,tanA=sin A（）⑵若∠A+∠B=900，则sinA= ，tanA.tanB= 】提分必练：1.如图，△ABC的顶点都在方格纸的格点上，则sinA=____.2.如图，已知点P的坐标是（a，b），则sinα等于（）A B C2.把△ABC三边的长度都扩大为原来的3倍，则A.不变B.缩小为原来的B.C.扩大为原来的3倍 D.不能确定4.如图，已知AB是⊙O的直径，点C、D在⊙O上，且AB＝5，BC＝3．则sin∠BAC= ；sin∠ADC= ．A(t，3)在第一象限，OA与x轴所夹的锐角为α,tanα=，则t的值是( )A.1B.1.5C.2D.3知识点2 直角三角形的边角关系：在Rt∠ABC中，∠C=900 三边分别为a、b、c⑴三边关系：⑵两锐角关系⑶边角之间的关系：sinA=cosB= _；cosA=sinB= __；tanA ; tanB提分必练：1.在Rt△ABC中，∠C=90°，已知∠A，b，解此直角三角形就是要求出( )A.cB.a，cC.∠B，a，cD.∠B，a，c，△ABC的面积2.在Rt△ABC中，若∠C=90°，AC=1，BC=2，则下列结论中正确的是( )A.sinB=B.cosB=C.tanB=2D.cosB=3.如图，在△ABC中，AC=6，BC=5，sinA=，则tanB=____.4.如图，在菱形ABCD中，DE⊥AB于点E，cosA=，BE=4，则tan∠DBE的值是____.abbaD31235552213253AabcBCAabcA BEFQ P知识点3 解直角三角形的实际应用【名师提醒：1.在解直角三角形实际应用中，先构造符合题意的三角形，解题的关键是弄清在哪个直角三角形中用多少度角的哪种锐角三角函数解决；(2)解直角三角形，当所求元素不在直角三角形中时，应作辅助线构造直角三角形，或寻找已知直角三角形中的边角替代所要求的元素；(3)解实际问题的关键是构造几何模型，大多数问题都需要添加适当的辅助线，将问题转化为直角三角形中的边角计算问题】 提分必练：1. 如图是某货站传送货物的平面示意图. 为了 提高传送过程的安全性，工人师傅欲减小 传送带与地面的夹角，使其由45°改为30°. 已知原传送带AB 长为4米. （1）求新传送带AC 的长度；（2）如果需要在货物着地点C 的左侧留出2米的通道，试判断距离B 点4米的货物MNQP 是否需要挪走，并说明理由．(说明：⑴⑵的计算结果精确到0.1米，参考数据：≈1.41， ≈1.73，≈2.24，≈2.45)第 2． 如图，大海中有A 和B 两个岛屿，为测量它们之间的距离，在海岸线PQ 上点E 处测得∠AEP ＝74°，∠BEQ ＝30°；在点F 处测得∠AFP ＝60°，∠BF Q ＝60°，EF ＝1km ．（1）判断ABAE 的数量关系，并说明理由；（2）求两个岛屿A 和B 之间的距离（结果精确到0.1km ）．（参考数据：3≈1.73，sin74°≈，cos74°≈0.28，tan74°≈3.49，sin76°≈0.97，cos76°≈0.24）3.在一个阳光明媚、清风徐来的周末，小明和小强一起到郊外放风筝﹒他们把风筝放飞后，将两个风筝的引线一端都固定在地面上的C 处(如图).现已知风筝A 的引线（线段AC ）长20m ，风筝B 的引线（线段BC ）长24m ，在C 处测得风筝A 的仰角为60°，风筝B 的仰角为45°.（1）试通过计算，比较风筝A 与风筝B 谁离地面更高？ （2）求风筝A 与风筝B 的水平距离. (精确到0.01 m ；参考数据：sin45°≈0.707,cos45°≈0.707,tan45°=1,sin 60°≈0.866,cos60°=0.5,tan 60°≈1.7322356(第6题【聚焦遵义中考】命题点1 解直角三角形1.如图，由四个边长为1的小正方形构成一个大正方形，连接小正方形的三个顶点，可得到△ABC，则△ABC中BC边上的高是________．2.如图，在平面直角坐标系中，点P(3，m)是第一象限内的点，且OP与x轴正半轴的夹角α的正切值为43，则sinα的值为()A.45B.54C.35D.533.如图，Rt△ABC中，∠BAC＝90°，AD⊥BC于点D，若BD∶CD＝3∶2，则tan B＝()A.32B.23C.62D.634.△ABC中，∠C＝90°，AB＝8，cos A＝34，则BC的长为________．命题点2 解直角三角形应用举例1.如图，河堤横断面迎水坡AB的坡比是1∶3，堤高BC＝10m，则坡面AB的长度是()A．15m B．203m C．20m D．103m2.如图，在小山的东侧A点有一个热气球，由于受西风的影响，以30米/分的速度沿与地面成75°角的方向飞行，25分钟后到达C处，此时热气球上的人测得小山西侧B点的俯角为30°，则小山东西两侧A、B两点间的距离为________米．3.如图所示，从热气球C处测得地面A、B两点的俯角分别为30°，45°，如果此时热气球C处的高度CD为100米，点A、D、B在同一直线上，则A、B两点的距离是()A．100(3＋1)米B．100(2＋1)米C．50(3＋1)米D．50(2＋1)米5.如图是某儿童乐园为小朋友设计的滑梯平面图．已知BC＝4米，AB＝6米，中间平台宽度DE＝1米，EN、DM、CB为三根垂直于AB的支柱，垂足分别为N、M、B，∠EAB＝31°，DF⊥BC于F，∠CDF＝45°，求DM和BC的水平距离BM的长度．(结果精确到0.1米，参考数据：sin31°≈0.52，cos31°≈0.86，tan31°≈0.60)6.如图，一楼房AB后有一假山，其坡度为i＝1∶3，山坡坡面上点E处有一休息亭，测得假山坡脚C与楼房水平距离BC＝25米，与亭子距离CE＝20米，小丽从楼房顶测得点E的俯角为45°，求楼房AB的高．(注：坡度i是指坡面的铅直高度与水平宽度的比)7.我市某中学在创建“特色校园”的活动中，将本校的办学理念做成宣传牌(AB)，放置在教学楼的顶部(如图所示)．小明在操场上的点D 处，用1米高的测角仪CD ，从点C 测得宣传牌的底部B 的仰角为37°，然后向教学楼正方向走了4米到达点F 处，又从点E 处测得宣传牌的顶部A 的仰角为45°.已知教学楼高BM ＝17米，且点A 、B 、M 在同一直线上，求宣传牌AB 的高度．(结果精确到0.1米，参考数据：3≈1.73，sin 37°≈0.60，cos 37°≈0.80，tan 37°≈0.75)8.为促进我市经济的快速发展，加快道路建设，某高速公路建设工程中需修隧道AB ，如图，在山外一点C 测得BC 距离为200m ，∠CAB ＝54°，∠CBA ＝30°，求隧道AB 的长．(参考数据：sin 54°≈0.81，cos 54°≈0.59，tan 54°≈1.38，3≈1.73，结果精确到个位)9.某市为缓解城市交通压力，决定修建人行天桥，原设计天桥的楼梯长AB ＝6m ，∠ABC ＝45°，后考虑到安全因素，将楼梯脚B 移到CB 延长线上点D 处，使∠ADC ＝30°(如图所示)．(1)求调整后楼梯AD 的长； (2)求BD 的长．(结果保留根号)9.如图，一水库大坝的横断面为梯形ABCD ，坝顶BC 宽6米，坝高20米，斜坡AB 的坡度i ＝1∶2.5，斜坡CD 的坡角为30°，求坝底AD 的长度．(精确到0.1米，参考数据：2≈1.414，3≈1.732.提示：坡度等于坡面的铅垂高度与水平长度之比)10.如图，海中有一灯塔P ，它的周围8海里内有暗礁．海轮以18海里/时的速度由西向东航行，在A 处测得灯塔P 在北偏东60°方向上；航行40分钟到达B 处，测得灯塔P 在北偏东30°方向上；如果海轮不改变航线继续向东航行，有没有触礁的危险？。

锐角三角函数知识点锐角三角函数是指以锐角为自变量的三角函数，包括正弦函数（sin）、余弦函数（cos）、正切函数（tan），以及它们的倒数函数（csc、sec、cot）。

1. 正弦函数（sin）：在直角三角形中，正弦函数定义为对边与斜边的比值，即sinθ = 对边/斜边。

正弦函数的定义域是锐角，即0到π/2。

它是一个奇函数，也就是sin(-θ) = -sinθ，且其值域是[-1,1]。

2. 余弦函数（cos）：在直角三角形中，余弦函数定义为邻边与斜边的比值，即cosθ = 邻边/斜边。

余弦函数的定义域是锐角，即0到π/2。

它是一个偶函数，也就是cos(-θ) = cosθ，且其值域是[-1,1]。

3. 正切函数（tan）：在直角三角形中，正切函数定义为对边与邻边的比值，即tanθ = 对边/邻边。

正切函数的定义域是锐角，即0到π/2，且不包含π/2。

它是一个奇函数，也就是tan(-θ) = -tanθ，且其值域是实数集。

4. 余割函数（csc）：余割函数是正弦函数的倒数，即cscθ = 1/sinθ。

它的定义域是锐角，除去sinθ=0的点，即θ ≠ kπ，其中k为整数。

它的值域为负无穷到负无穷。

5. 正割函数（sec）：正割函数是余弦函数的倒数，即secθ = 1/cosθ。

它的定义域是锐角，除去cosθ=0的点，即θ ≠(k+1/2)π，其中k为整数。

它的值域为负无穷到负无穷。

6. 余切函数（cot）：余切函数是正切函数的倒数，即cotθ = 1/tanθ。

它的定义域是锐角，除去tanθ=0的点，即θ ≠ kπ，其中k为整数。

它的值域为负无穷到负无穷。

锐角三角函数在数学和物理中广泛应用，可以用于解决与三角形、周期性现象和振荡等相关的问题。

锐角三角函数知识点一：锐角三角函数的定义： 一、 锐角三角函数定义：在Rt △ABC 中，∠C=900, ∠A 、∠B 、∠C 的对边分别为a 、b 、c ， 则∠A 的正弦可表示为：sinA= ， ∠A 的余弦可表示为cosA=∠A 的正切：tanA= ，它们弦称为∠A 的锐角三角函数 特别提醒：1、sinA 、cosA 、tanA 表示的是一个整体，是两条线段的比，没有d 单位，这些比值只与 有关，与直角三角形的 无关例1．如图所示，在Rt △ABC 中，∠C ＝90°．①斜边)(sin =A ＝______， 斜边)(sin =B ＝______； ②斜边)(cos =A ＝______，斜边)(cos =B ＝______；③的邻边A A ∠=)(tan ＝______，)(tan 的对边B B ∠=＝______2、取值范围 <sinA< ， cosA< tanA>3 特殊角的三角函数值例2．求适合下列条件的锐角α ．(1)21cos =α (2)222sin =α (3)33)16cos(6=- α练习 1（2013•本溪）（1）计算：+（x ﹣2）0﹣﹣2cos45°2（2013•孝感）式子的值是（ ）BD3（8分）（2013•沈阳）计算：．4、(2013年广东湛江)阅读下面的材料，先完成阅读填空，再将要求答题：1sin 30,cos302οο==22sin 30cos 30οο+= ； ① sin 4545οο==22sin 45cos 45οο+= ； ②sin 6060οο==22sin 60cos 60οο+= ． ③ ……观察上述等式，猜想：对任意锐角A ，都有22sin cos A A += 1 ．④ （１）如图，在锐角三角形ABC 中，利用三角函数的定义及勾股定理 对A ∠证明你的猜想； （２）已知：A ∠为锐角()cos 0A >且3sin 5A =，求cos A 4 增减性：当 时，正弦和正切值随着角度的增大而 余弦值随着角度的增大而 例3 三角函数的增减性 1．已知∠A 为锐角，且sin A <21，那么∠A 的取值范围是 A. 0°< A < 30° B. 30°< A ＜60° C. 60°< A < 90° D. 30°< A < 90° 2. 已知A 为锐角，且030sin cos <A ，则 （ ）A. 0°< A < 60°B. 30°< A < 60°C. 60°< A < 90°D. 30°< A < 90° 典型例题：类型一：直角三角形求值3．（3分）（2013•盘锦）如图，矩形ABCD 的边AB 上有一点P ，且AD=，BP=，以点P 为直角顶点的直角三角形两条直角边分别交线段DC ，线段BC 于点E ，F ，连接EF ，则tan ∠PEF= _________ ．类型二. 利用角度转化求值：4（2013•南通）如图，正方形ABCD 的边长为4，点M 在边DC 上，M 、N 两点关 于对角线AC 对称，若DM =1，则tan ∠ADN = ▲ ．5（2013•自贡）如图，边长为1的小正方形网格中，⊙O 的圆心在格点上，则∠AED 的余弦值是 ．A （第17题）BDM NC··6、（2013•荆门）如图，在半径为1的⊙O 中，∠AOB=45°，则sinC 的值为（ ）．CD的延长线于E ，则sin ∠E 的值为（ ）8、(2013年深圳市)如图3，已知321////l l l ，相邻两条平行直线间的距离相等，若等腰直角△ABC 的三个项点分别在这三条平行直线上，则αsin 的值是（ ）A.31 B.176 C.55 D.1010类型三. 化斜三角形为直角三角形10、（2013•曲靖）如图，在直角梯形ABCD 中，AD ∥BC ，∠B=90°，∠C=45°，AD=1，BC=4，则CD= ．11（西城二模）1．如图，四边形ABCD 中，∠BAD=135°，∠BCD=90°，tan ∠BDC= 63．(1) 求BD 的长； (2) 求AD 的长．类型四：利用网格构造直角三角形13（2013•宿迁）如图，将AOB ∠放置在55⨯的正方形网格中，则tan AOB ∠的值是 A ．23 B ．32C D第4题图AOB类型五：仰角与俯角： 14．（3分）（2013•大连）如图，为了测量河的宽度AB ，测量人员在高21m 的建筑物CD 的顶端D 处测得河岸B 处的俯角为45°，测得河对岸A 处的俯角为30°（A 、B 、C 在同一条直线上），则河的宽度AB 约为 _________ m （精确到0.1m ）．（参考数据：≈1.41，，1.73）类型六. 坡度与坡角15（2012•广安）如图，某水库堤坝横断面迎水坡AB 的坡比是1高BC=50m ，则应水坡面AB 的长度是（ ）A ．100mB ．mC ．150mD ．26（10分）（2013•锦州）如图，某公司入口处有一斜坡AB ，坡角为12°，AB 的长为3m ，施工队准备将斜坡修成三级台阶，台阶高度均为hcm ，深度均为30cm ，设台阶的起点为C ． （1）求AC 的长度；（2）求每级台阶的高度h ．（参考数据：sin12°≈0.2079，cos12°≈0.9781，tan12°≈0.2126．结果都精确到0.1cm ）类型七. 方位角 17．已知：如图，一艘货轮向正北方向航行，在点A 处测得灯塔M 在北偏西30°，货轮以每小时20海里的速度航行，1小时后到达B 处，测得灯塔M 在北偏西45°，问该货轮继续向北航行时，与灯塔M 之间的最短距离是多少?(精确到0.1海里，732.13 ) 综合18（2013•呼和浩特）如图，AD 是△ABC 的角平分线，以点C 为圆心，CD 为半径作圆交BC 的延长线于点E ，交AD 于点F ，交AE 于点M ，且∠B=∠CAE ，EF ：FD=4：3． （1）求证：点F 是AD 的中点；（2）求cos ∠AED 的值；（3）如果BD=10，求半径CD 的长．。