高三开学摸底考试

2024届高三下学期开学摸底考试卷（）生物（考试时间：90分钟试卷满分：100分）注意事项：1．本试卷分第Ⅰ卷（选择题）和第Ⅰ卷（非选择题）两部分。

答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。

2．回答第Ⅰ卷时，选出每小题答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

写在本试卷上无效。

3．回答第Ⅰ卷时，将答案写在答题卡上。

写在本试卷上无效。

4．考试结束后，将本试卷和答题卡一并交回。

一、选择题：本题共19个小题，每小题2分，共38分。

每小题只有一个选项符合题目要求。

1．某城市因生活污水的大量排放，导致河流严重污染，水华频发，鱼类等水生动物大量死亡，同时还散发出阵阵恶臭，严重影响人们的生活。

近年来政府花大力气整治环境，将生活污水通过管道引到污水处理厂进行净化处理，达标后排放，固体垃圾集中分类处理，河道清淤、引水稀释，斜坡修绿道，种花草等措施，使该河流面貌焕然一新。

下列相关叙述错误的是（）A．该河流从污染严重到焕然一新的过程中发生了群落的次生演替B．通过治理，该区域为人们提供了休闲场所体现出生物多样性的间接价值C．与治理前相比，该河道生态系统的抵抗力稳定性得到提高D．该事例说明，人类活动也可以使群落朝着物种增多、结构复杂的方向演替2.建国后我国人口政策主要经历了：第1阶段，1949年始鼓励生育；第2阶段，1979年始计划生育；第3阶段，2016年始开放和鼓励生育。

下列关于人口政策改变的理解，错误的是（）A．第2阶段政策实施的目的是防止自然资源短缺、环境恶化B．第3阶段政策实施的目的是改善我国人口年龄结构C．第2阶段政策实施后人口仍然保持增长与我国医学科技的进步有关D．三个阶段政策均通过控制人口出生率和死亡率达到目的3.代谢性碱中毒是指体内酸丢失过多或者从体外进入碱过多的情况，主要表现为血浆HCO3过高，pH值升高。

呼吸性碱中毒是指由于肺通气过度，使血浆H2CO3浓度或CO2分压原发性减少，导致pH值升高。

2024届新高三开学摸底考试综合训练卷注意事项：1．答卷前，考生务必将自己的姓名、考生号等填写在答题卡和试卷指定位置上。

2．回答选择题时，选出每小题答案后，用铅笔把答题卡对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

回答非选择题时，将答案写在答题卡上。

写在本试卷上无效。

3．考试结束后，将本试卷和答题卡一并交回。

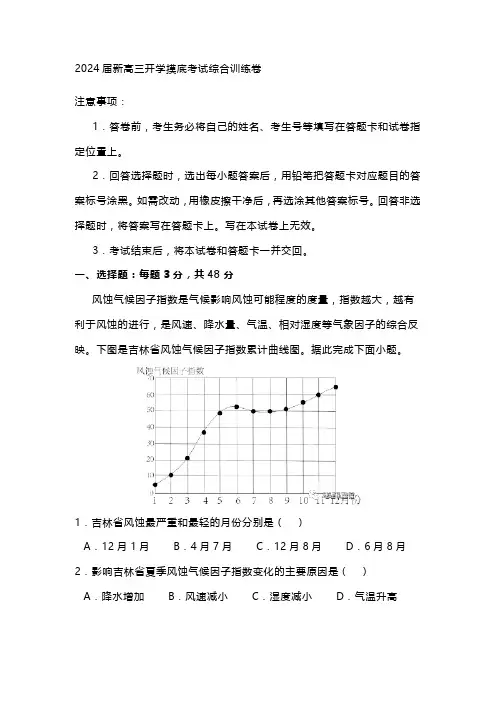
一、选择题：每题3分，共48分风蚀气候因子指数是气候影响风蚀可能程度的度量，指数越大，越有利于风蚀的进行，是风速、降水量、气温、相对湿度等气象因子的综合反映。

下图是吉林省风蚀气候因子指数累计曲线图。

据此完成下面小题。

1．吉林省风蚀最严重和最轻的月份分别是（）A．12月1月 B．4月7月 C．12月8月 D．6月8月2．影响吉林省夏季风蚀气候因子指数变化的主要原因是（）A．降水增加 B．风速减小 C．湿度减小 D．气温升高青海S藏毯生产公司成立于2007年，产品远销欧美、中东等40多个国家。

近年来S公司通过引进世界著名纱织企业F集团入驻青海，实现了从原料加工到产品出口的整个生产流程。

目前S公司推出了个性化定制藏毯项目，可根据用户需求进行设计与快速制作。

读下图，完成下面小题。

3．S公司引进F集团的最主要目的是（）A．利用共用基础设施，形成产业集聚B．提高藏毯研发水平和质量C．扩大市场需求，促进当地经济发展D．减少运输环节，降低生产成本4．个性化定制对S公司发展的影响主要表现在（）A．提高公司知名度和经济效益 B．优化产品结构，加快产业转型C．进一步加强与F集团的合作 D．提高研发能力，保持品牌优势黄河下游河床由于泥沙淤积，在大堤的束缚下不断抬高形成地上悬河。

某悬河段两岸农民曾在主河槽两侧自发加建新堤。

下图为该悬河段横断面示意图。

据此完成下面小题。

5．农民在大堤内自发加建新堤的主要目的是（）A．增加流速，提高河段冲淤能力 B．减少水流对黄河大堤的冲刷C．促进泥沙淤积，提高土壤肥力 D．扩大耕地面积，提高经济收入6．自建堤可能导致该河段（）A．洪水发生频率增加 B．河道摆动更加频繁C．大堤冲决风险减小 D．形成新一级的悬河土壤容重指一定容积的土壤烘干后质量与烘干前体积的比值，有机质含量较高的土壤疏松多孔。

2025届高考（新高考卷）高三年级开学摸底考试试卷英语注意事项：1．答卷前，考生务必将自己的姓名、考生号等填写在答题卡和试卷指定位置上。

2．回答选择题时，选出每小题答案后，用铅笔把答题卡对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

回答非选择题时，将答案写在答题卡上。

写在本试卷上无效。

3．考试结束后，将本试卷和答题卡一并交回。

第一部分：听力（共两节，满分30 分）第一节听下面 5 段对话。

每段对话后有一个小题,从题中所给的A、B、C 三个选项中选出最佳选项。

听完每段对话后，你都有10 秒钟的时间来回答有关小题和阅读下一小题。

每段对话仅读一遍。

1．What is the weather like now?A．Snowy. B．Sunny. C．Rainy.2．What will the man do next month?A．Buy a car. B．Fix his car. C．Take a driving test.3．How does the woman normally eat carrots?A．She cooks them. B．She eats them raw. C．She makes juice out of them.4．What is the probable relationship between the speakers?A．Friends. B．Brother and sister. C．Doctor and patient.5．When will the speakers meet?A．At 5:00 p. m. on Friday. B．At 5:00 a. m. on Friday. C．At 5 :00 p.m. on Saturday.第二节听下面 5 段对话或独白。

每段对话或独白后有几个小题,从题中所给的A、B、C 三个选项中选出最佳选项。

2025届贵阳市高三语文上学期开学摸底考试卷考试时间：150分钟试卷满分：150分2024.08一、现代文阅读（35分）(一）现代文阅读I(本题共5小题，19分）阅读下面的文字，完成1~5题。

材料一：硅基智能近日宣布开源其最新的AI数字人交互平台，使用者无需组建技术团队，利用平台提供的丰富工具和支持，就可在智能手机、平板电脑、大屏幕等显示设备上，轻松创建数字人。

从影视娱乐到品牌营销，从电商直播到金融服务，数字人深入各行各业，并重塑商业生态，数字人应用已成为人工智能企业竞相角逐的新赛道。

天眼查数据显示，截至目前，我国现存与数字人相关的企业114.4万家，其中，2024年1~5月，新增注册企业为17.4万余家，与2023年同期相比增加5.9%。

“这么多年了，终于见到了梦中的母亲！”家住重庆沙坪坝区的漆女士，随着年龄增长越发思念早逝的母亲，最近她花费近两万元，制作了一个母亲的数字人，第一次与“母亲”视频对话，她喜极而泣。

当前，用科技手段“复活”亲人已经萌发出较强的市场需求。

重庆某技术团队负责人告诉记者，业务开展一年来，已接到2000多人的询问，帮助900多个家庭通过AI技术实现“团圆”，收费从几千元到上万元不等。

从去年“双11”到最近的“6·18”，国内各大电商平台直播间上线多个数字人主播，这些“主播”不仅“照片级别”复刻了真人表情动作，还24小时直播带货，流利解答消费者疑问，推荐多种省钱团购……据统计，目前在中国从事视频表演等活动的主播账号有近1.4亿个，其中虚拟数字人占了四成，超过5000万个。

艾媒咨询提供的《2023年中国虚拟人产业发展与商业趋势研究报告》显示，2022年中国虚拟人带动产业市场规模和核心市场规模分别为1866.1亿元和120.8亿元，预计2025年分别达到6402.7亿元和480.6亿元。

虚拟数字人作为元宇宙重要的细分赛道之一，目前被拓展到文旅行业的更多场景中。

中传文旅（北京）文化发展有限公司研发的数字人“华诗远”，成为文旅行业有代表性的数字员工、数字导游和数字主播，在提高人们文旅体验的同时，还帮助文旅企业降本增效、提升服务水平，推动行业数字化转型和创新发展。

安徽省A10联盟2025届高三上学期开学摸底考试语文试题一、现代文阅读 (35分)(一)现代文阅读Ⅰ (本题共5小题，19分)阅读下面的文字，完成1~5题。

材料一：和形而上学的宇宙观相反，唯物辩证法的宇宙观主张从事物的内部、从一事物对他寜物的关系去研究事物的发展，即把事物的发展看做是事物内部的必然的自己的运动，而每一事物的运动都和它的周围其他事物互相联系着和互相影响着。

事物发展的根本原因，不是在事物的外部而是在事物的内部，在孺物内部的矛盾性。

任何事物内部都有这种矛盾性，因此引起了事物的运动和发展。

事物内部的这种矛盾性是事物发展的根本原因，一事物和他事物的互相联系和互相影响则是事物发展的第二位的原因。

这样，唯物辩证法就有力地反对了形而上学的机械唯物论和庸俗进化论的外因论或被动论。

这是清楚的，单纯的外部原因只能引起事物的机械的运动，即范围的大小，数量的增减，不能说明事物何以有性质上的千差万别及其互相变化。

事实上，即使是外力推动的机械运动，也要通过事物内部的矛盾性。

植物和动物的单纯的增长，数量的发展，主要地也是由于内部矛盾所引起的。

同样，社会的发展，主要地不是由于外因而是由于内因。

许多国家在差不多一样的地理和气候的条件下，它们发展的差异性和不平衡性，非常之大。

同一个国家吧，在地理和气候并没有变化的情形下，社会的变化却是很大的。

帝国主义的俄国变为社会主义的苏联，封建的闭关锁国的日本变为帝国主义’的日本，这些国家的地理和气候并没有变化。

长期地被封建制度统治的中国，近百年来发生了很大的变化，现在正在变化到一个自由解放的新中国的方向去，中国的地理和气候并没有变化。

整个地球及地球各部分的地理和气候也是变化着的，但以它们的变化和社会的变化相比较，则显得很微小，前者是以若干万年为单位而显现其变化的，后者则在几千年、几百年、几十年、甚至几年或几个月(在革命时期)内就显现其变化了。

按照唯物辩证法的观点，自然界的变化，主要地是由于自然界内部矛盾的发展。

2025届新高三年级开学摸底考试卷数 学（考试时间：120分钟 试卷满分：150分）注意事项：1．答卷前，考生务必将自己的姓名、准考证号等填写在答题卡和试卷指定位置上。

2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

回答非选择题时，将答案写在答卡上。

写在本试卷上无效。

3．考试结束后，将本试卷和答题卡一并交回。

第一部分（选择题 共58分）一、选择题：本题共8小题，每小题5分，共40分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．已知集合{23}A xx =-<<∣，{}250,B x x x x =-<∈N ∣，则A B = （ ） A ．{03}xx <<∣ B ．{25}x x -<<∣ C ．{0,1,2} D ．{1,2}2．已知复数z 满足4i2i z z -=-，则z 的虚部为（ ） A ．1i 5B ．1i 10 C ．15D ．1103．已知π(0,),3sin 2cos 212ααα∈=+，则tan 2α=（ ）AB C ．34D ．434．若命题：“a ∃，R b ∈，使得cos cos a b b a -≤-”为假命题，则a ，b 的大小关系为（ ） A ．a b <B ．a b >C ．a b ≤D ．a b ≥5．黄地绿彩云龙纹盘是收藏于中国国家博物馆的一件明代国宝级瓷器．该龙纹盘敞口，弧壁，广底，圈足．器内施白釉，外壁以黄釉为地，刻云龙纹并填绿彩，美不胜收．黄地绿彩云龙纹盘可近似看作是圆台和圆柱的组合体，其口径22.5cm ，足径14.4cm ，高3.8cm ，其中底部圆柱高0.8cm ，则黄地绿彩云龙纹盘的侧面积约为（ ）（附：π的值取35≈）A ．2311.31cmB ．2300.88cmC ．2322.24cmD ．2332.52cm6．某校开展数学建模活动，有建模课题组的学生选择测量某山峰的高度，为此，他们设计了测量方案．如图，在山脚A 测得山顶P 的仰角为45°，沿倾斜角为15°的斜坡向上走了90米到达B 点（A ，B ，P ，Q 在同一个平面内），在B 处测得山顶P 的仰角为60°，则山高PQ 为（ ）米A ．B ．C ．1)-D ．1)7．已知双曲线E ：()222210,0x y a b a b-=>>的左、右焦点分别为1F ，2F ，过2F 的直线与E 的右支交于A ，B两点，且222BF AF =，若10AF AB ⋅=，则双曲线E 的离心率为（ ）AB C D 8．已知函数()f x 的定义域为R ，且满足()()()22,(1)2f x f y f x y xy f +=+-+=，则下列结论正确的是（ ） A ．(4)12f = B ．方程()f x x =有解 C ．12f x ⎛⎫+ ⎪⎝⎭是偶函数D ．12f x ⎛⎫- ⎪⎝⎭是偶函数二、选择题：本题共3小题，每小题6分，共18分．在每小题给出的选项中，有多项符合题目要求．全部选对的得6分，部分选对的得部分分，有选错的得0分．9．某次数学考试后，为分析学生的学习情况，某校从某年级中随机抽取了100名学生的成绩，整理得到如图所示的频率分布直方图.为进一步分析高分学生的成绩分布情况，计算得到这100名学生中，成绩位于[)80,90内的学生成绩方差为12，成绩位于[)90,100内的同学成绩方差为10.则（ ）参考公式：样本划分为2层，各层的容量､平均数和方差分别为：m 、x 、21s ；n 、y 、22s .记样本平均数为ω，样本方差为2s ，()()2222212m n s s x s y m n m n ωω⎡⎤⎡⎤=+-++-⎣⎦⎣⎦++.A ．0.004a =B ．估计该年级学生成绩的中位数约为77.14C ．估计该年级成绩在80分及以上的学生成绩的平均数为87.50D ．估计该年级成绩在80分及以上的学生成绩的方差为30.2510．已知函数π()sin 33f x x ⎛⎫=+ ⎪⎝⎭，下列说法正确的是（ ）A ．()f x 的最小正周期为2π3B ．点π,06⎛⎫⎪⎝⎭为()f x 图象的一个对称中心C ．若()(R)f x a a =∈在ππ,189x ⎡⎤∈-⎢⎥⎣⎦上有两个实数根，则12a ≤<D ．若()f x 的导函数为()f x '，则函数()()y f x f x =+'11．已知1x 是函数 ()()30f x x mx n m =++<的极值点，若()()()2112f x f x x x =≠，则下列结论 正确的是（ ）A ．()f x 的对称中心为()0,nB ．()()11f x f x ->C ．1220x x +=D ．120x x +>第二部分（非选择题 共92分）三、填空题：本题共3小题，每小题5分，共15分。

2025届高三开学摸底联考语文试题注意事项：1．答卷前，考生务必将自己的姓名、考场号、座位号、准考证号填写在答题卡上。

2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案标号。

回答非选择题时，将答案写在答题卡上，写在本试卷上无效。

3．考试结束后，将本试卷和答题卡一并交回。

考试时间150分钟，满分150分一、现代文阅读（35分）（一）现代文阅读Ⅰ（本题共5小题，19分）阅读下面的文字，完成1~5题。

材料一：在一个具有高度干扰性和沉重信息负担的环境中，我们往往会感觉到备受影响而无法集中精神。

其实，令我们觉得注意力难以集中的一个可能的原因，与需求和能力之间的差异有关。

换句话说，我们所感知到的只是一个“相对的”注意力缺陷。

信息应激。

为了使我们的心智功能得到开发，我们有没有必要无条件地接收信息洪流呢？不，没这个必要。

我们必须时常提醒自己，我们在接受信息的尺度方面总是有极限的。

当要求超越了我们的能力时会发生什么，边开车边打电话所造成的事故就是最实在的警示。

另一个告诉我们在拥抱汹涌的信息洪流时应该有所保留的因素，就是它与应激之间的关联。

我们对于应激的了解在近些年得到了深化，无数的研究证明，高水平的应激激素会损害心脏、血管、免疫系统等我们身体几乎所有的部分，包括大脑。

对大脑而言，加剧的应激与工作记忆受损和长时记忆受损都有密切的联系。

科学家证明，应激，尤其是特定的几种类型，例如创伤后的应激，能够影响海马，这是一个对在长时记忆中储存信息非常重要的脑部结构。

但这只是对于长期的、高水平的应激而言，中度或暂时性的应激可能是有益处的，如对唤醒具有最佳效果。

应激激素与信息量之间也没有任何简单的联系。

在《为什么斑马不会得溃疡》一书中，萨波斯基综述了他与其他人在应激方面，以及与之有关的深层原因的研究。

应激水平与情境相关，并受到我们对自身所处状况的解读的影响。

“可控感”是一个很关键的概念。

物理试卷注意事项：1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。

2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

回答非选择题时，将答案写在答题卡上。

写在本试卷上无效。

3．考试结束后，将本试题卷和答题卡一并交回。

一、选择题：本题共10小题，共46分。

在每小题给出的四个选项中，第1~7题只有一项符合题目要求，每小题4分；第8~10题有多项符合题目要求，每小题6分，全部选对的得6分，选对但不全的得3分，有选错的得0分。

1. 受特大地磁暴影响，2024年5月11日凌晨，我国新疆、北京、内蒙古等地出现极光。

磁暴产生的高能带电粒子与大气中氧原子发生作用而使氧原子被激发至高能级，氧原子的电子从高能级向低能级跃迁时发出特定波长的光，形成不同颜色的极光。

北京的天文爱好者拍摄到的极光呈红色，而内蒙古的天文爱好者拍摄到的极光呈绿色。

关于不同地区极光，下列说法正确的是（ ）A. 北京红色极光的波长小于内蒙古绿色极光的波长B. 北京红色极光的能量大于内蒙古绿色极光的能量C. 氧原子的电子从高能级向低能级跃迁时两能级差值北京比内蒙古小D. 用北京红色极光照射某金属表面可发生光电效应，如果改用内蒙古绿色极光照射该金属表面不一定能发生光电效应2. 现代生活中共享电动车已成为一种新型的短途交通工具，通过扫码开锁，循环共享，方便快捷。

一辆共享电动车所用电池是锂电池，骑行在一段倾角不太大的坡路上加速上坡过程中，在此过程中电能向其他形式能量转化，下列说法正确的是（ ）A. 电能转化为动能和重力势能B. 电能转化为重力势能和内能C. 电能转化成动能和内能D. 电能转化为机械能和内能3. 波源的振动在介质中产生一列沿x 轴方向传播的简谐横波，从某一时刻开始计时坐标原点处质点的振动图像如图甲所示，时的波形如图乙所示，质点P 平衡位置的横坐标为，则下列说法正确的是（ ）0.2s t =5m x =A. 该简谐波沿x 轴正方向传播B. 时刻质点P 正沿y 轴负方向运动C. 如果将波源的振动周期增大为，则简谐波波速为D. 如果将波源的振动周期增大为，则简谐波波速为4. 某同学在学习了奥斯特实验和磁场的相关知识后设计了一个测量微弱磁场的实验装置。

高三化学考试本试卷满分100分，考试用时75分钟。

注意事项：1．答题前，考生务必将自己的姓名、考生号、考场号、座位号填写在答题卡上。

2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

回答非选择题时，将答案写在答题卡上，写在本试卷上无效。

3．考试结束后，将本试卷和答题卡一并交回。

4．本试卷主要考试内容：高考全部内容。

5．可能用到的相对原子质量：H 1 C 12 O 16 Sc 45 Zn 65 Se 79一、选择题：本题共14小题，每小题3分，共42分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．古文中记载了火法炼锌工艺，其过程为取炉甘石（主要成分为）十斤，装载入泥罐内，然后逐层用煤炭饼垫盛……，冷定，毁罐取出……，即倭铅（金属锌）也。

该工艺涉及反应：。

下列说法错误的是（ ）A ．锌元素位于元素周期表第四周期ⅡB 族B ．CO 分子中含键和键，属于非极性分子C ．“冷定，毁罐取出”能防止锌被氧化D ．反应所涉及的物质属于不同的晶体类型2．下列玻璃仪器选择合理且能完成相应实验（夹持装置略去）的是（）① ② ③ ④ ⑤ ⑥ ⑦ ⑧ ⑨A ．配制的硫酸溶液：①④⑤⑨B ．分离四氮化碳和碘单质的混合物：③④⑥C ．测定晶体中结晶水的含量：③⑤⑦⑧D ．用饱和碳酸钠溶液提纯乙酸乙酯（含少量乙酸）：②⑤3．科技创新是赢得未来发展主动权的必然选择。

下列说法错误的是（ ）A ．“天机芯”是全球首款异构融合类电脑芯片，其主要成分和光导纤维的相同B．合成纤维是以石油等为原料制成有机小分子单体，再聚合生产而成的3ZnCO 3ZnCO 2CZn 3CO ++↑高温σπ500mL40%42CuSO 5H O ⋅C ．碳纤维材料操纵棒是航天员手臂“延长器”，碳纤维属于新型无机非金属材料D ．用二氧化碳合成葡萄糖，为人工合成“粮食”提供了新路径，葡萄糖属于多羟基醛4．下列离子方程式书写正确的是（）A ．氢氟酸蚀刻玻璃：B ．将通入水中制硝酸：C ．向新制氯水中滳入溶液：D ．金属Na 与溶液反应：5．物质结构决定物质性质。

济南2024届高三开学摸底考语文真题及答案解析山东省济南市2024届高三下学期开学考试语文试题注意事项：1.本试卷满分150分，考试时间150分钟。

2.答卷前，考生务必将自己的姓名、座号、考生号填写在答题卡上，并将条形码横贴在答题卡的“贴条形码区”。

3.作答选择题时，选出每小题答案后，用2B铅笔把答题卡上对应题目选项的答案信息点涂黑;如需改动，用橡皮擦干净后，再选涂其他答案，答案不能答在试卷上。

4.非选择题必须用直径0.5毫米黑色字迹钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上;如需改动，先划掉原来的答案，然后再写上新的答案;不准使用铅笔和涂改液，不按以上要求作答的答案无效。

5.考生必须保持答题卡的整洁。

考试结束后，将试卷和答题卡一并交回。

一、现代文阅读(35分)(一)现代文阅读I(本题共5小题，19分)阅读下面的文字，完成1-5题材料一：我国自古就有声诗统一的传统，从艺术起源看，诗、乐、舞三位一体，在先秦时期便是如此。

《诗经》与《楚辞》实则都是可以演唱的歌词。

到两汉和魏晋南北朝时期，乐府诗还是可以演唱的，甚至唐代时，还有乐工可以歌唱汉魏乐府诗。

到了唐代，除了乐府诗以外，一部分或五言、或七言的近体诗(律诗和绝句)也可以演唱。

但唐代大部分的诗都不能演唱了。

宋诗不能唱，代之而起的是可以演唱的词。

元代又有了可以演唱的曲子，即套曲和小令。

诗词既然能唱，就应该有乐谱。

现在我们能够见到的最早乐谱是在敦煌藏经洞里发现的唐代琵琶乐谱和现藏于日本阳明文库的原近卫家所藏唐五弦琵琶谱，但都有谱无诗。

南宋朱熹《仪礼经传通解》收录的南宋赵彦肃传的《风雅十二诗谱》，是为《诗经》所配的曲子。

如果确实是唐开元年间传下来的诗谱的话，它应该是流传下来的最早的声诗兼备的诗谱，即最早的诗歌曲。

中国古代曲谱都有曲与歌词同载的习惯，唐宋以来有文字谱、减字谱、俗字谱、律吕谱、工尺谱等复杂的记谱法。

南宋姜夔曾把唐代名曲《霓裳曲》中的两段曲谱破译成当时流行的俗字谱，以便时人歌唱。

2025届新高三开学摸底考试卷（新高考Ⅰ卷专用）01语文（考试时间：150分钟试卷满分：150分）注意事项：1．答卷前，考生务必将自己的姓名、准考证号等填写在答题卡和试卷指定位置上。

2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

回答非选择题时，将答案写在答题卡上。

写在本试卷上无效。

3．考试结束后，将本试卷和答题卡一并交回。

一、现代文阅读（35分）（一）现代文阅读Ⅰ(本题共5小题，18分)阅读下面的文字，完成下面小题。

材料一：1921年10月，瑞典人安特生与中央地质调查研究所袁复礼等人，在仰韶村开始正式发掘。

根据出土文物，安特生判断此地为中国远古文化遗存，并依照国际考古学惯例命名为仰韶文化。

仰韶文化的发掘，是我国第一次有组织、有计划的科学考古发掘，标志着中国现代考古学的建立，填补了中国远古文化发展史尤其是石器时代的空白。

安特生虽然在仰韶文化遗址的发现上有开山之功，推翻了西方考古界关于中国无石器时代的“论断”，但他毕竟不是考古学科班出身，在发掘过程中没能采用考古类型学、地层学的分析方法，他错误地判断仰韶村只有仰韶文化一种类型。

另外，受制于当时欧洲中心主义思潮盛行的时代背景，他在判断仰韶文化起源上出现了严重的失误。

仰韶文化以彩陶为重要特色，在对仰韶村遗址进行正式发掘前，安特生在查找彩陶考古资料时，注意到美国考古学者庞贝利1904年在中亚发掘安诺遗址的报告。

安特生发现，安诺遗址出土的彩陶与自己在仰韶村发现的彩陶的花纹样式十分相像，于是有了仰韶文化从中亚传播而来的假说，但他又一时无法打通仰韶遗址与安诺遗址在文化传播上的地理链条关系。

为了验证自己的假说，从1923年起，安特生开始赴甘肃、青海等地进行考察。

他发现，甘肃、青海地区出土的彩陶，比仰韶出土彩陶工艺技术更为先进，却很少见到代表中原文化的陶鬲、陶鼎等器物，且当时中国并没有比仰韶彩陶更早的彩陶出土，而欧洲、中亚多有史前彩陶发掘。

2025届新高三开学摸底考试卷（新九省地区专用）数 学（考试时间：120分钟 试卷满分：150分）注意事项：1．答卷前，考生务必将自己的姓名、准考证号等填写在答题卡和试卷指定位置上。

2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

回答非选择题时，将答案写在答卡上。

写在本试卷上无效。

3．考试结束后，将本试卷和答题卡一并交回。

一、单项选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一个选项是符合题目要求的．1．已知全集U =R ，集合(){}23|0,log 221x A x B x x x -⎧⎫=∈≤=+⎨⎬+⎩⎭Z ，则U A B =I ð（ ） A ．{}12x x -≤≤∣ B ．{12}xx -<≤∣ C ．{}0,1,2D ．{}1,0,1,2-2．在复平面内，复数12,z z 对应的点关于直线y x =对称，若12i z =+，则213i z +-=（ ） AB ．5CD ．13．已知向量(2,4),(3,1)a b ==-，则“k =()()a kb a kb +⊥- ”的（ ） A ．充分不必要条件 B ．必要不充分条件 C ．充分必要条件D ．既不充分也不必要条件 4．已知()()()1sin 2cos ,tan 2αβαβαβ-=+-=，则tan tan αβ-=（ ） A ．35B ．53C ．45D ．655．已知正四棱台1111ABCD A B C D -32π的球面上，且该球的球心在底面ABCD 上，则棱台1111ABCD A B C D -的体积为（ ） AB．CD．6．已知函数()21sin π4f x x x x ⎛⎫=-+ ⎪⎝⎭，则方程()1f x =在区间[]2,3-上的所有实根之和为（ ）A ．2B ．4C ．6D ．87．设数列{}n a 的前n 项和为n S ，112a =，121n n na a a +=+，若()2024,1S k k ∈+，则正整数k 的值为（ ）A ．2024B ．2023C ．2022D ．20218．对于函数()y f x =和()y g x =，及区间D ，若存在实数k b ､，使得()()f x kx b g x ≥+≥对任意x D ∈恒成立，则称()y f x =在区间D 上“优于”()y g x =.有以下两个结论：①()2log f x x =在区间[]1,2D =上优于()2(1)g x x =-；②()32f x x =+在区间[]1,1D =-上优于()e x g x =.那么（ ） A ．①､②均正确 B ．①正确，②错误 C ．①错误，②正确D ．①､②均错误二、选择题：本题共3小题，每小题6分，共18分．在每小题给出的选项中，有多项符合题目要求．全部选对的得6分，部分选对的得部分分，有选错的得0分． 9．下列说法中正确的是（ ）A ．从一批含有10件正品、4件次品的产品中任取3件，则取得2件次品的概率是4591B ．已知随机变量X 服从二项分布(,)B n p ，若()20,()10E X D X ==，则40n =C ．已知随机变量ξ服从正态分布()22,N σ，若(1)P p ξ>=，则(3)1P p ξ<=-D ．已知随机事件A ，B 满足32(),()55P B P AB ==，则1()3P AB =∣ 10．关于函数()12ln f x x x=+，下列判断正确的是（ ） A ．12x =是()f x 的极大值点 B ．函数()y f x x =-有且只有1个零点 C ．对1k >不等式()f x kx <在[)1,+∞上恒成立D ．对任意两个正实数12,x x ，且12x x >，若()()12f x f x =，则121x x +>11．已知()()1122,,,P x y Q x y 是曲线222:7666321C x y y x y -+++-=上不同的两点，O 为坐标原点，则（ ）A ．2211x y +的最小值为3B ．24≤≤C ．若直线3y kx =+与曲线C 有公共点，则,k ⎛⎫∈-∞+∞ ⎪ ⎪⎝⎭D ．对任意位于y 轴左侧且不在x 轴上的点P ，都存在点Q ，使得曲线C 在,P Q 两点处的切线垂直 三、填空题：本题共3小题，每小题5分，共15分．12．已知双曲线22221x y a b-=的左焦点为F ，P 为渐近线位于第一象限内的点，过原点O 作直线AB 平行于FP ，交双曲线于A ，B 两点，四边形FPBA 为矩形，则该双曲线的离心率为 ．13．已知直线:l y kx =是曲线()1e xf x +=和()lng x x a =+的公切线，则实数a = ．14．一个书包中有标号为“1,1,2,2,3,3,,,n n ”的2n 张卡片.一个人每次从中拿出一张卡片，并且不放回；如果他拿出一张与已拿出的卡片中有相同标号的卡片，则他将两张卡片都扔掉；如果他手中有3张单张卡片或者书包中卡片全部被拿走，则操作结束.记书包中卡片全部被拿走的概率为n P ，则3P = .7P = .四、解答题：本题共5小题，共77分．解答应写出文字说明、证明过程或演算步骤． 15．（13分）在ABC 中，已知角A ，B ，C 所对的边分别为a ，b ，c ，()223sin sin 222B A aba b a b c +=++． (1)求角C 的大小；(2)若ABC 为锐角三角形，求a bc+的取值范围． 16．（15分）已知椭圆()222210x y a b a b +=>>的左、右焦点分别为12F F ，，点P 的坐标为()a b ，，且线段OP(1)求椭圆的离心率e ；(2)若直线2PF 交椭圆于M N ，两点（M 在N 的上方），过2F 作PN 的垂线l 交y 轴于点D ，若线段2DF 延长线上的一个点H 满足DPH △2． ①证明四边形DPHN 是菱形； ②若243DF =，求椭圆的方程．17．（15分）如图，在四棱锥P ABCD -中，平面PAD ⊥平面ABCD ，AB AD ⊥，5AB AD +=，CD =120PAD ∠=︒，=45ADC ∠︒.(1)求证：平面PAB ⊥平面PAD ； (2)设AB AP =.①若直线PB 与平面PCD AB 的长.②在线段AD 上是否存在点G ，使得点P ，C ，D 在以G 为球心的球上？若存在，求线段AB 的长；若不存在，说明理由.18．（17分）已知函数()e 2,,e xf x ax a =--ÎR 是自然对数的底数.(1)若1a =，证明：()1f x ≥-；(2)若关于x 的方程()20f x +=有两个不相等的实根，求a 的取值范围； (3)若1,a k =为整数，且当0x >时，不等式()11k xf x x -'<+恒成立，求k 的最大值. 19．（17分）中国女排是中国各体育团队中成绩突出的体育团队之一，曾是世界上第一个“五连冠”得主，并十度成为世界冠军，2023年在杭州第19届亚运会上女排再度获得冠军．她们那种团结协作、顽强拼搏的精神极大地激发了中国人的自豪、自尊和自信，为我们在新征程上奋进提供了强大的精神力量．如今，女排精神广为传颂，家喻户晓，各行各业的人们在女排精神的激励下，为中华民族的腾飞顽强拼搏．某中学也因此掀起了排球运动的热潮，在一次排球训练课上，体育老师安排4人一组进行传接球训练，其中甲、乙、丙、丁四人刚好围成一个矩形（如图），已知当某人控球时，传给其相邻同学的概率为25，传给对角线上的同学的概率为15，由甲开始传球．(1)求第3次传球是由乙传给甲的概率； (2)求第n 次传球后排球传到丙手中的概率；(3)若随机变量i X 服从两点分布，且()()110i i i P X P X q ==-==，1i =，2，…，n ，则11n ni i i i E X q ==⎛⎫= ⎪⎝⎭∑∑，记前n 次（即从第1次到第n 次传球）中排球传到乙手中的次数为Y ，求()E Y ．参考答案一、单项选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一个选项是符合题目要求的．1．已知全集U =R ，集合(){}23|0,log 221x A x B x x x -⎧⎫=∈≤=+⎨⎬+⎩⎭Z ，则U A B =I ð（ ） A ．{}12x x -≤≤∣ B ．{12}xx -<≤∣ C ．{}0,1,2 D ．{}1,0,1,2-【答案】C【分析】解分式不等式求解集合A ，解对数函数不等式得集合B ，然后利用补集运算和交集运算求解即可. 【详解】由301x x -≤+得()()31010x x x ⎧-+≤⎨+≠⎩，解得13x -<≤.又x ∈Z ，所以{}0,1,2,3A =. 由()22log 22log 4x +>=，得2x >，所以{2}B x x =>∣，所以{}2U B x x =≤∣ð， 所以{}0,1,2U A B ⋂=ð. 故选：C .2．在复平面内，复数12,z z 对应的点关于直线y x =对称，若12i z =+，则213i z +-=（ ）A B ．5C D ．1【答案】C【分析】由12,z z 关于直线y x =对称求出2z ，再根据复数模的定义计算即可． 【详解】因为12i z =+，所以其对应点为()2,1，()2,1关于直线y x =对称的点为()1,2，则212i z =+，所以213i 12i 13i 2i z +-=++-=-= 故选：C ．3．已知向量(2,4),(3,1)a b ==- ，则“k =是“()()a kb a kb +⊥-”的（ ）A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件【答案】A【分析】先计算()()a kb a kb +⊥- 时k 的取值，再根据必要与充分条件的定义判断即可.【详解】因为(2,4)a =，(3,1)b =- ，所以()+23,4a kb k k =+- ，()23,4a kb k k -=-+，当()()a kb a kb +⊥-时，()()·0a kb a kb +-=，即(23)(23)(4)(4)0k k k k +-+-+=解得k =所以“k =是()()a kb a kb +⊥-的充分不必要条件.故选：A.4．已知()()()1sin 2cos ,tan 2αβαβαβ-=+-=，则tan tan αβ-=（ ） A ．35B ．53C ．45D ．65【答案】C【分析】利用两角和差的正余弦公式展开，两边同除cos cos αβ，得到tan tan tan tan 12αβαβ-⋅=-.再利用两角差的正切公式展开()tan αβ-，将tan tan αβ⋅换成tan tan 12αβ--，化简即可得到答案.【详解】()()sin 2cos αβαβ-=+，所以()sin cos cos sin 2cos cos sin sin αβαβαβαβ-=-， 两边同除cos cos αβ，得到tan tan 22tan tan αβαβ-=-⋅，即tan tan tan tan 12αβαβ-⋅=-.()tan tan tan tan 1tan tan tan 1tan tan 2112αβαβαβαβαβ---===-+⋅+-，4tan tan 5αβ∴-=.故选：C.5．已知正四棱台1111ABCD A B C D -32π的球面上，且该球的球心在底面ABCD 上，则棱台1111ABCD A B C D -的体积为（ ） AB．CD．【答案】C【分析】利用棱台及其外接球的特征结合台体体积公式计算即可. 【详解】设球心为O ，球O 的半径为R ，棱台高为h ，则24π32πR =，所以R =，由于O 在底面ABCD 上，底面ABCD 为正方形， 易得正方形ABCD4=，面积为16； 设底面1111D C B A 的外接圆半径为r，则r == 易得正方形1111D C B A2=，面积为4；所以正四棱台1111ABCD A B C D -的体积为(11643V =⨯+=. 故选:C ．6．已知函数()21sin π4f x x x x ⎛⎫=-+ ⎪⎝⎭，则方程()1f x =在区间[]2,3-上的所有实根之和为（ ）A ．2B ．4C ．6D ．8【答案】A【分析】首先确定()f x 的图象关于12x =对称，然后分12x =和12x ≠两种情况进行讨论，利用数形结合的方法，在同一直角坐标系中画出sin πy x =、 2112y x =⎛⎫- ⎪⎝⎭，通过判断两函数在1,32⎛⎤ ⎥⎝⎦上的交点个数即可求出函数()1f x =的实根和.【详解】因为()2211sin πsin π42f x x x x x x ⎛⎫⎛⎫=-+=- ⎪ ⎪⎝⎭⎝⎭，则()()()221111sin π1sin π22f x x x x x f x ⎛⎫⎛⎫⎡⎤-=---=-= ⎪ ⎪⎣⎦⎝⎭⎝⎭， 所以()f x 的图象关于12x =对称，因为102f ⎛⎫= ⎪⎝⎭，此时()1f x =不成立， 当12x ≠时，由()1f x =，即21sin π12x x ⎛⎫-= ⎪⎝⎭，则21sin π12x x =⎛⎫- ⎪⎝⎭， ()214sin 2π09122=<=⎛⎫- ⎪⎝⎭，2511sin π1245122⎛⎫=>= ⎪⎝⎭⎛⎫- ⎪⎝⎭，214sin 3π025132=<=⎛⎫- ⎪⎝⎭， 在同一平面直角坐标系中画出2112y x =⎛⎫- ⎪⎝⎭与sin πy x =，[]2,3x ∈-的图象如下所示：由图可得2112y x =⎛⎫- ⎪⎝⎭与sin πy x =在1,32⎛⎤ ⎥⎝⎦上有且仅有2个交点，图象都关于12x =， 所以所有的实根之和为122⨯=. 故选：A【点睛】关键点点睛：本题关键是判断出()f x 关于12x =对称，再将方程的解转化为函数与函数的交点横坐标，根据对称性计算.7．设数列{}n a 的前n 项和为n S ，112a =，121nn na a a+=+，若()2024,1S k k ∈+，则正整数k 的值为（ ） A ．2024 B ．2023C ．2022D ．2021【答案】C【分析】根据递推关系，构造等比数列求出通项公式，再由分组求和及放缩法得出n S 的范围即可. 【详解】由121n n n a a a +=+，两边取倒数可得：111122n n a a +=+， 即1111112n n a a +⎛⎫-=- ⎪⎝⎭，又111n a -=，所以11n a ⎧⎫-⎨⎬⎩⎭是首项为1，公比为12的等比数列， 所以111111*********n n n n n n a a a ----=⇒=+⇒=-+， 故011111212121n n S n -⎛⎫=-++⋯+ ⎪+++⎝⎭， 令011111212121n M -=++⋯++++ 由112112n n -<+且3n ≥，则32111151112322642n n M -⎛⎫>++++=+- ⎪⎝⎭ ，由1111212n n --<+，则0111111212222n nM -⎛⎫<+++=- ⎪⎝⎭， 则1113122122nn nn S n --+<<-+，所以20242023202411112022202220232122S +<<++<， 故()20242022,2023S ∈，则正整数k 的值为2022． 故选：C8．对于函数()y f x =和()y g x =，及区间D ，若存在实数k b ､，使得()()f x kx b g x ≥+≥对任意x D ∈恒成立，则称()y f x =在区间D 上“优于”()y g x =.有以下两个结论：①()2log f x x =在区间[]1,2D =上优于()2(1)g x x =-；②()32f x x =+在区间[]1,1D =-上优于()e x g x =.那么（ ） A ．①､②均正确 B ．①正确，②错误 C ．①错误，②正确 D ．①､②均错误【答案】A【分析】在同一个平面直角坐标系作出函数(),()y f x y g x ==在区间D 上的图形，由题意给的定义，根据数形结合的数学思想依次判断即可求解.【详解】①：当1x =时，(1)0,(1)0f g ==；当2x =时，(2)1,(2)1f g ==， 所以函数(),()f x g x 图象都经过点(1,0),(2,1)A B ， 则直线AB 的方程为()100121y x --=--，即1y x =-， 在同一个平面直角坐标系作出函数(),()y f x y g x ==在区间[]1,2上的图形，如图，由图可知，()()()22log 11f x x y x g x x =³=-³=-，即存在1,1k b ==-使得()()f x kx b g x ≥+≥在区间[]1,2上恒成立， 所以()2log f x x =在区间[]1,2D =上优于()()21g x x =-，故①正确；②：问题等同于()3f x x =在区间[]1,1D =-上优于()e 2xg x =-在同一个平面直角坐标系作出函数(),()y f x y g x ==在区间[]1,1D =-上的图形，如图，由图可得，()()11e 2,1e 2g g -=--=-，即()()11,e 2,1,e 2A B ----，所以直线AB 的方程为()()1e 2e 2e 212y x ---+--=-，即11e e e e e 222y x ----=+--.设曲线3()f x x =在()()3000,0,x x x >处且平行于直线AB 的切线为l ，由()2003l k f x x ¢==，//l AB ，得120e e 32x --=，解得0x =则切点，所以1e e :2l y x -æ-ç-=-ççè，即1e e 2y x --=取e 2.7=，则1e e 0.47e 20.482---≈-->-， 所以切线l 位于直线AB 的下方，则存在实数,k b 使得()()3e 2x f x x y kx b g x =³=+³=+，即()32f x x =+在区间[]1,1D =-上优于()e x g x =，故②正确.故选：A.【点睛】关键点点睛：本题关键在于理解函数新定义，利用导数研究不等式恒成立，和导数的几何意义；在利用导数求切线方程时，可用导数的意义求出切线的斜率.二、选择题：本题共3小题，每小题6分，共18分．在每小题给出的选项中，有多项符合题目要求．全部选对的得6分，部分选对的得部分分，有选错的得0分． 9．下列说法中正确的是（ ）A ．从一批含有10件正品、4件次品的产品中任取3件，则取得2件次品的概率是4591B ．已知随机变量X 服从二项分布(,)B n p ，若()20,()10E X D X ==，则40n =C ．已知随机变量ξ服从正态分布()22,N σ，若(1)P p ξ>=，则(3)1P p ξ<=-D ．已知随机事件A ，B 满足32(),()55P B P AB ==，则1()3P AB =∣ 【答案】BD【分析】对A ，根据超几何分布可计算判断；对B ，由二项分布的均值和方差公式计算判断；对C ，根据正态分布的对称性求出概率判断；对D ，根据全概率和条件概率的计算公式求解.【详解】对于A ，从一批含有10件正品、4件次品的产品中任取3件，则取得2件次品的概率为21410314C C 61015C 1413291p ⋅⨯===⨯⨯，故A 错误； 对于B ，(),X B n p ~ ，()20110np np p =⎧∴⎨-=⎩，解得4012n p =⎧⎪⎨=⎪⎩，故B 正确；对于C ，()22,N ξσ ，则正态曲线的对称轴为2ξ=，根据正态曲线的对称性可得()()13P P p ξξ>=<=，故C 错误；对于D ，()()()P B P AB P AB =+ ，()321555P AB ∴=-=， 所以()()()115335P AB P A B P B ===，故D 正确. 故选：BD.10．关于函数()12ln f x x x=+，下列判断正确的是（ ） A ．12x =是()f x 的极大值点B ．函数()y f x x =-有且只有1个零点C ．对1k >不等式()f x kx <在[)1,+∞上恒成立D ．对任意两个正实数12,x x ，且12x x >，若()()12f x f x =，则121x x +> 【答案】BCD【分析】对于A ，直接对函数()12ln f x x x=+求导研究即可；对于B ，构造函数()()12ln x x x g x f x x =-=+-，求导，利用单调性来判断即可；对于C ，将问题转化为()212ln f x x k x x x>=+在[1,)∞+上恒成立，构造函数()212ln xh x x x=+，求其最大值即可；对于D ，将问题转化为证明()()1f x f x >-，10,2x ⎛⎫∈ ⎪⎝⎭，构造函数()()()1g t f t f t =--，利用导数求其最值可得答案. 【详解】对于A ，()12ln f x x x=+ ，()221221x x x x f x -'∴=-+=，当102x <<时，()0f x '<，函数()12ln f x x x =+在10,2⎛⎫⎪⎝⎭上单调递减， 当12x >时，()0f x ¢>，函数()12ln f x x x =+在1,2⎛⎫+∞ ⎪⎝⎭上单调递增， 12x ∴=为()f x 的极小值点，A 错误； 对于B ，()()12ln x x xg x f x x =-=+-， 则()()22211210x g x x x x --'=-+-=≤，所以函数()g x 在()0,∞+上单调递减， 又()112ln110g =+-=，所以函数()y f x x =-有且只有1个零点，B 正确； 对于C ，若()f x kx <在[1,)∞+上恒成立， 得()212ln f x xk x x x>=+在[1,)∞+上恒成立， 则2max 12ln x k x x ⎡⎤>+⎢⎥⎣⎦，令()212ln xh x x x =+，则()323222ln 222ln x x x x h x x x x ---+-'=+=， 令()222ln k x x x x =-+-，()2ln k x x '=-， 当[1,)x ∞∈+时，()0k x '≤，()k x 单调递减，()()1222ln 20k x k ∴≤=-+-=，即()0h x '≤，()h x ∴在[1,)∞+上单调递减，故函数()()max 11h x h ==，则1k >，C 正确；对于D ， 令10,2t ⎛⎫∈ ⎪⎝⎭，()()()()()11122ln 2ln 12ln 1111g tt t tt f t f t t t t t t -=+-=----=+---，则()()()()()()()()222222211212211120111t t t t t t t t t t t t t t g t -----'----+=+⨯⨯=<--- ()g t ∴在10,2⎛⎫⎪⎝⎭上单调递减，则()012g t g ⎛⎫>= ⎪⎝⎭，即()()10f t f t -->， 10,2t ⎛⎫∈ ⎪⎝⎭，12x x > ，()()12f x f x =，结合A 选项可得122111,0,1222x x x ><<->，()()221f x f x ∴>-，()()121f x f x ∴>-，函数()12ln f x x x =+在1,2⎛⎫+∞ ⎪⎝⎭上单调递增， 则121x x >-，121x x +>即对任意两个正实数12,x x ，且12x x >，若()()12f x f x =，则121x x +>，D 正确. 故选：BCD.【点睛】关键点点睛：本题难点在选项D ，将问题转化为证明()()1f x f x >-，10,2x ⎛⎫∈ ⎪⎝⎭是关键，然后构造出函数()()()1g t f t f t =--来解决问题.11．已知()()1122,,,P x y Q x y 是曲线222:7666321C x y y x y -+++-=上不同的两点，O 为坐标原点，则（ ）A ．2211x y +的最小值为3B ．24≤+≤C ．若直线3y kx =+与曲线C 有公共点，则,k ⎛⎫∈-∞+∞ ⎪ ⎪⎝⎭D ．对任意位于y 轴左侧且不在x 轴上的点P ，都存在点Q ，使得曲线C 在,P Q 两点处的切线垂直 【答案】BCD【分析】根据题中曲线表达式去绝对值化简，根据表达式求值判定A ，根据几何意义判断B ，根据直线与椭圆的位置关系判断C ，根据图形特征以及切线概念判断D.【详解】当2630x y +-≥时，原方程即2227666321x y y x y -+++-=，化简为22143y x +=，轨迹为椭圆，将22334y x =-代入2630x y +-≥，解得08y ≤≤，则此时02y ≤≤，即此部分为椭圆的一半，当2630x y +-<时，原方程即()2227666321x y y x y -+-+-=，化简得()2214x y +-=，将()2241x y =--代入2630x y +-<，解得2y >或0y <， 则此时10y -≤<，即此部分为圆的一部分，作出曲线的图形如下：选项A ：当0y ≥时，1222221111333344y x y y y =-++=+≥，当10y =时取最小值3，当0y <时，()2222111114123x y y y y +=--+=+，当11y =-时取最小值1，则2211x y +的最小值为1，故A 错误；选项B ()11,x y 与点()0,1和点()0,1-的距离之和，当0y ≥时，点()0,1和点()0,1-为椭圆22143y x +=的焦点，，当0y <时，点()0,1为圆()2214x y +-=的圆心，点()0,1-在圆()2214x y +-=上，2当点P 在()或)最大，且为2，[]2,4，即24≤≤，故B 正确；选项C ：直线3y kx =+过定点()0,3，当直线经过()或)时，直线斜率k =，联立221433y x y kx ⎧+=⎪⎨⎪=+⎩，化简得()224318150k x kx +++=， 因直线3y kx =+与曲线C 有公共点，即()()22Δ18443150k k =-+⨯≥，解得k ≥k ≤， 所以直线3y kx =+与曲线C有公共点时,k ∞∞⎛⎫∈-⋃+ ⎪ ⎪⎝⎭，故C 正确； 选项D ：当点P 在椭圆上时，对任意位于y 轴左侧且不在x 轴上的点P ， 则曲线C 在点P 处的切线斜率可以取任何非零正实数，曲线C 在y 轴右侧椭圆部分切线斜率也可以取到任何非零负实数，使得两切线斜率为负倒数， 同理，当点P 在圆上时，对任意位于y 轴左侧且不在x 轴上的点P ， 则曲线C 在点P 处的切线斜率可以取任何非零负实数，曲线C 在y 轴右侧圆部分切线斜率也可以取到任何非零正实数，使得两切线斜率为负倒数，所以对任意位于y 轴左侧且不在x 轴上的点P ，都存在点Q ，使得曲线C 在,P Q 两点处的切线垂直，故D 正确； 故选：BCD.【点睛】方法点睛：本题考查解析几何的综合问题，此类问题常见的处理方法为： （1）几何法：通过图形特征转化，结合适当的辅助线与图形关系进而求解；（2）坐标法：在平面直角坐标系中，通过坐标的运算与转化，运用方程联立与韦达定理等知识，用坐标运算求解答案.三、填空题：本题共3小题，每小题5分，共15分．12．已知双曲线22221x y a b-=的左焦点为F ，P 为渐近线位于第一象限内的点，过原点O 作直线AB 平行于FP ， 交双曲线于A ，B 两点，四边形FPBA 为矩形，则该双曲线的离心率为 ．1【分析】由已知，可得P 点坐标为(),a b ，由双曲线的性质可得B 为PE 的中点，则得,22a c b B +⎛⎫⎪⎝⎭，代入双曲线方程，化简即可解出双曲线的离心率. 【详解】由已知，四边形FPBA 为矩形，可知O 为AB 的中点，所以OP OF c ==， 设P 点坐标为(),x y ，则22222x y c a b +==+， 又P 在渐近线by x a=上，联立解得(),P a b ， 延长PB 交x 轴于点E ，由对称性可得E 为双曲线的右焦点，则B 为PE 的中点，则,22a c b B +⎛⎫⎪⎝⎭，代入22221x y a b-=化简得，22240c ac a +-=， 则得2240e e +-=，解得1e =-（负值舍去）.1.13．已知直线:l y kx =是曲线()1e xf x +=和()lng x x a =+的公切线，则实数a = ．【答案】3【分析】先设在()y f x =上的切点，然后求出切点和切线，然后再设在()y g x =上的切点，即可求出a 的值.【详解】设直线l 与曲线()y f x =相切于点()00,x y ，由()1e x f x +'=，得()010e x k f x +'==，因为l 与曲线()1e xf x +=相切，所以0010010e ,e ,x x y x y ++⎧=⎪⎨=⎪⎩消去0y ，得00110e e x x x ++=，解得01x =． 设l 与曲线()y g x =相切于点()11,x y ，由()1g x x'=，得211e k x ==，即21e 1x =，因为()11,x y 是l 与曲线()ln g x x a =+的公共点，所以21111e ,ln ,y x y x a ⎧=⎨=+⎩消去1y ，得211e ln x x a =+，即211ln e a =+，解得3a =．故答案为：3.14．一个书包中有标号为“1,1,2,2,3,3,,,n n ”的2n 张卡片.一个人每次从中拿出一张卡片，并且不放回；如果他拿出一张与已拿出的卡片中有相同标号的卡片，则他将两张卡片都扔掉；如果他手中有3张单张卡片或者书包中卡片全部被拿走，则操作结束.记书包中卡片全部被拿走的概率为n P ，则3P =.7P =.【答案】35/0.6 275005【分析】先求出他手中3张单张卡片含有2张相同卡片的概率，进而得出n P 和1n P -间的递推关系，用累乘方法求解73,P P 即可.【详解】2n 张卡片选取3张卡片的选法共有：32C n 种，事件“手中这3张单张卡片中含有2张相同卡片”的选法共有：(22)n n -种； 由古典概型的计算公式可得其概率为：32(22)3C 21nn n n -=-， 若书包中2n 张卡片全部被拿走的概率为n P ，将这两张相同的卡片拿掉以后，相当于从1n -对相同的卡片中已拿出一张卡，事件“书包中2n 张卡片全部被拿走”发生需保证事件“书包中22n -卡片全部被拿走”发生， 且书包中22n -卡片全部被拿走概率为1n P -， 因而1321n n P P n -=-，且21P =， 则32332315P P ==⨯-，7333332713119755005P =⨯⨯⨯⨯=， 故答案是：35（或0.6），275005. 【点睛】思路点睛：本题主要考查递推数列与概率知识的交汇问题，解决该类问题应该注意的事项有： （1）做好互斥事件的划分，正确进行独立事件概率的计算；（2）借助待定系数方法建立不同事件概率间的递推关系，即构建递推数列； （3）正确运用数列求通项公式或求和的方法解决问题.四、解答题：本题共5小题，共77分．解答应写出文字说明、证明过程或演算步骤． 15．（13分）在ABC 中，已知角A ，B ，C 所对的边分别为a ，b ，c ，()223sin sin 222B A ab a b a b c +=++． (1)求角C 的大小；(2)若ABC 为锐角三角形，求a bc+的取值范围． 【答案】(1)π3C =(2)2⎤⎦【分析】（1）由二倍角的正弦和余弦公式，结合余弦定理将角转化为边，可将式子变形为222a b c ab +-=，再利用余弦定理即可求解；（2）利用正弦定理将边转化为角，再结合三角恒等变换可得π2sin 6a b A c +⎛⎫=+ ⎪⎝⎭，根据锐角三角形可得A 的取值范围，结合三角函数的图象和性质即可求解. 【详解】（1）在ABC 中，()()221cos 1cos cos cos sin sin 222222a Bb A B A a b a B b A a b --+++=+=-()22222211cos cos 222222a b a b a c b b c a a B b A a b ac bc ⎛⎫+++-+-=-+=-⨯+⨯ ⎪⎝⎭2a b c+-=， 因为()223sinsin 222B A ab a b a b c +=++， 所以()322a b c ab a b c +-=++， 化简得222a b c ab +-=，由余弦定理得2221cos 22a b c C ab +-==，又()0,πC ∈，所以π3C =；..........................................................6分 （2）由正弦定理知2πsin sin sin sin 3πsin sin 3A A a b AB cC ⎛⎫+- ⎪++⎝⎭==13sin sin sin 22A A A A A ⎫⎫=+=⎪⎪⎪⎪⎭⎭1π2cos 2sin 26A A A ⎫⎛⎫=+=+⎪ ⎪⎪⎝⎭⎭， 由ABC 为锐角三角形可知π02π02A B ⎧<<⎪⎪⎨⎪<<⎪⎩，而π3C =，..........................................................9分 所以π022ππ032A A ⎧<<⎪⎪⎨⎪<-<⎪⎩得ππ62A <<，所以ππ2π363A <+<，πsin 16A ⎛⎫<+≤ ⎪⎝⎭，即π2sin 26A ⎛⎫<+≤ ⎪⎝⎭，则a bc+的取值范围为2⎤⎦...........................................................13分16．（15分）已知椭圆()222210x y a b a b +=>>的左、右焦点分别为12F F ，，点P 的坐标为()a b ，，且线段OP(1)求椭圆的离心率e ；(2)若直线2PF 交椭圆于M N ，两点（M 在N 的上方），过2F 作PN 的垂线l 交y 轴于点D ，若线段2DF 延长线上的一个点H 满足DPH △2． ①证明四边形DPHN 是菱形； ②若243DF =，求椭圆的方程． 【答案】(1)12;(2)①证明见解析 ；②2231164x y +=.【分析】（1）利用条件中线段长关系可构造齐次式求离心率；（2）①根据上问结论化简椭圆方程，分别求直线DH PN 、的方程，根据面积求出22DF F H =，再求出N 坐标，可判定22NF F P =，从而证明结论；②直接由243DF =解方程即可. 【详解】（1）由已知得长轴长为2a ，则2222134,4,22OPc a b a c e a a ===∴===；.........................................................3分 （2）① 证明：由（1）知22224,3==a c b c ，所以椭圆方程为2222143x y c c +=，易知()()22,,0P c F c ，所以2PF k ==，故直线DH 的方程为)y x c =-，直线PN 的方程为)y x c =-，令0x =，则2,,y D DF ⎛⎫=∴= ⎪ ⎪⎝⎭， 易知22PF c =，2211222PDF PDH S c S ∴=⨯==⇒ 22DF F H =，联立方程组)2222215240143y x c x cx x y c c ⎧=-⎪⇒-=⎨+=⎪⎩， 解得1280,5c x x ==， M 在N的上方，()20,,2N NF c ∴=，即22NF F P =，由上得，四边形DPHN 的对角线互相垂直且平分，故四边形DPHN 是菱形．..........................................................11分 ②解：由243DF c ==⇒，从而2a b ==， 即椭圆的方程为2231164x y +=...........................................................15分17．（15分）如图，在四棱锥P ABCD -中，平面PAD ⊥平面ABCD ，AB AD ⊥，5AB AD +=，CD =120PAD ∠=︒，=45ADC ∠︒.(1)求证：平面PAB ⊥平面PAD ； (2)设AB AP =.①若直线PB 与平面PCD，求线段AB 的长. ②在线段AD 上是否存在点G ，使得点P ，C ，D 在以G 为球心的球上？若存在，求线段AB 的长；若不存在，说明理由.【答案】(1)证明见解析(2)①2AB =或7023AB =；②不存在点G ，理由见解析【分析】（1）利用面面垂直的性质可证得AB ⊥平面PAD ，再利用面面垂直的判定定理即可证得结论； （2）①依题建系，设AB t =，利用题设条件，分别求得相关点和向量的坐标，利用空间向量坐标的夹角公式列出方程，求解即得t 的值；②假设存在点G ，可由GC GD =推得1GD =，得点G 坐标，由GP GD =得方程24150t t -+=，因此方程无实数解，假设不成立.【详解】（1）在四棱锥P ABCD -中，平面PAD ⊥平面ABCD ，AB AD ⊥， AB ⊂平面ABCD ，平面PAD ⋂平面ABCD AD =，所以AB ⊥平面PAD ，又AB ⊂平面PAB ，所以平面PAB ⊥平面PAD ..........................................................4分（2）如图以A 为原点，以AB 所在直线为x 轴，以AD 所在直线为y 轴建立如图所示直角空间坐标系A xyz -，设AB t =，则AP t =，由5AB AD +=，CD =120PAD ∠=︒，=45ADC ∠︒，则(),0,0B t，0,2t P ⎛- ⎝，因5AD t =-，则()0,5,0D t -，()1,4,0C t -，所以1,2t CP ⎛=-- ⎝ ，()1,1,0CD =-①设平面PCD 的法向量为(),,n x y z =，由n CP ⊥ ，n CD ⊥ ，得：8020t x y x y ⎧--+=⎪⎨⎪-+=⎩，可取n ⎛= ⎝设直线PB 与平面PCD 所成角为θ，则有：sin cos ,n BP θ=，,2t BP t ⎛=-- ⎝ ，2231161400t t-+=，解得2t=或7023t=，即2AB=或7023AB=...........................................................10分②如图，假设在线段AD上是否存在点G，使得点P，C，D在以G为球心的球上，由GC GD=，得45GCD GDC∠=∠=︒，所以90CGD∠=︒，所以cos451GD CD=︒=，又AB t=得5AD t=-，4AG AD GD t=-=-，所以()0,4,0G t-，0,2tP⎛-⎝由GP GD=得()22412tt⎡⎤---+=⎢⎥⎣⎦，即2234124tt⎛⎫-+=⎪⎝⎭，亦即24150t t-+=（*），因为()2Δ44150=--⨯<，所以方程（*）无实数解，所以线段AD上不存在点G，使得点P，C，D在以G为球心的球上 (15)分【点睛】方法点睛：本题主要考查利用空间向量解决线面所成角以及多点是否在同一球面上的开放性问题，属于较难题.根据题意，创建合适的空间直角坐标系，利用空间向量夹角的坐标表达式即可求解相关问题，对于开放性问题，一般是假设结论成立，通过推理计算求得结论成立的条件或者推导出矛盾.18．（17分）已知函数()e2,,exf x ax a=--ÎR是自然对数的底数.(1)若1a=，证明：()1f x≥-；(2)若关于x的方程()20f x+=有两个不相等的实根，求a的取值范围；(3)若1,a k=为整数，且当0x>时，不等式()11k xf xx-'<+恒成立，求k的最大值.【答案】(1)证明见解析(2)()e,+∞ (3)2【分析】（1）构造函数()e 1xx x ϕ=--，利用导函数求得函数单调性并求得其最值，可得结论；（2）将方程e 0xax -=有两个实根转化为函数y a =与函数()e xg x x=有2个交点，求得函数单调性结合图象可知e a >； （3）将不等式()11k xf x x '-<+恒成立转化为()()e 11x k x x --<+即可，构造函数并根据零点存在定理可得存在()01,2x ∈，满足002xe x =+，再结合单调性和零点范围可得k 的最大值为2.【详解】（1）若1a =，即证e 10x x --≥，设()e 1xx x ϕ=--，则()e 1x x ϕ'=-，由()0x ϕ'=，得0x =，所以当0x <时，()0x ϕ'<；当0x >时，()0x ϕ'>， 即()x ϕ在(),0∞-上单调递减，在()0,∞+上单调递增， 所以()x ϕ在0x =处取得最小值， 即()()00x ϕϕ≥=，即e 10x x --≥，所以可得()1f x ≥-...........................................................5分（2）方程()20f x +=，即e 0xax -=，显然当0x =时，方程不成立，则e ,0xa x x=≠，若方程有两个不等实根，即函数y a =与函数()e xg x x=有2个交点，易知()()21e x x g x x -'=， 当()(),00,1x ∞∈-⋃时，()()0,g x g x '<在区间(),0∞-和()0,1上单调递减， 当(),0x ∞∈-时，()0g x <，当()0,1x ∈时，()0g x > 当()1,x ∞∈+时，()()0,g x g x '>在()1,∞+上单调递增， 所以当0x >时，1x =时，()g x 取得最小值，且()1e g =， 且0x +→时，()g x ∞→+，当x →+∞时，()g x ∞→+ 其图象如图所：，结合图象可知y a =与()xe g x x=有2个交点，则e a >；因此a 的取值范围为()e,+∞.........................................................11分（3）当1a =时，()()e 2,e 1x xf x x f x '=--=-，所以0x >时，()11k xf x x '-<+，也即()()e 11x k x x --<+， 当0x >时，1e 10,e 1xx x k x +-><+-， 令()1,0e 1x x h x x x +=+>-，则()()()()22e e 2e 11e 1e 1x x x x x x x h x ----=+=-'-， 令()e 2,0xm x x x =-->当0x >时，()e 10xm x ='->，则()e 2x m x x =--在()0,∞+单调递增，又易知()()10,20m m ，所以()m x 在()0,∞+上存在唯一的零点，即()h x '在()0,∞+上存在唯一的零点，设此零点为0x ，则()01,2x ∈，且002xe x =+，当()00,x x ∈时，()()0,h x h x '<单调递减，当()0,x x ∞∈+时，()()0,h x h x '>单调递增， 所以()h x 的最小值为()()00000112,3e 1x x h x x x +=+=+∈-， 所以()0k h x <，即可得整数k 的最大值为2..........................................................17分【点睛】关键点点睛：不等式恒成立问题往往通过构造函数将问题转化成求函数最值问题，再利用导函数得出函数单调性求得其最值，即可得出结论.19．（17分）中国女排是中国各体育团队中成绩突出的体育团队之一，曾是世界上第一个“五连冠”得主，并十度成为世界冠军，2023年在杭州第19届亚运会上女排再度获得冠军．她们那种团结协作、顽强拼搏的精神极大地激发了中国人的自豪、自尊和自信，为我们在新征程上奋进提供了强大的精神力量．如今，女排精神广为传颂，家喻户晓，各行各业的人们在女排精神的激励下，为中华民族的腾飞顽强拼搏．某中学也因此掀起了排球运动的热潮，在一次排球训练课上，体育老师安排4人一组进行传接球训练，其中甲、乙、丙、丁四人刚好围成一个矩形（如图），已知当某人控球时，传给其相邻同学的概率为25，传给对角线上的同学的概率为15，由甲开始传球．(1)求第3次传球是由乙传给甲的概率； (2)求第n 次传球后排球传到丙手中的概率；(3)若随机变量i X 服从两点分布，且()()110i i i P X P X q ==-==，1i =，2，…，n ，则11n ni i i i E X q ==⎛⎫= ⎪⎝⎭∑∑，记前n 次（即从第1次到第n 次传球）中排球传到乙手中的次数为Y ，求()E Y ． 【答案】(1)8125(2)14-11132545nn⎛⎫⎛⎫-+- ⎪ ⎪⎝⎭⎝⎭(3)4n +*331,325nn ⎡⎤⎛⎫--∈⎢⎥ ⎪⎝⎭⎢⎥⎣⎦N【分析】（1）设第n 次传球后排球在甲、乙、丙、丁手中的概率分别为*,,,,n n n n a b c d n ∈N ，得到11112120,,,555a b c d ====，求出2425b =，从而得到第3次传球是由乙传给甲的概率；（2）求出*,,,,n n n n a b c d n ∈N 之间的关系式，联立后得到15nn n a c ⎛⎫-=- ⎪⎝⎭，n n b d =，进而得到111254n n c ⎧⎫⎪⎪⎛⎫+--⎨⎬ ⎪⎝⎭⎪⎪⎩⎭是以11111325420c ⎛⎫+--=- ⎪⎝⎭为首项，公比为35-的等比数列，求出1111342545n nn c ⎛⎫⎛⎫=--+- ⎪ ⎪⎝⎭⎝⎭；（3）在（2）的基础上求出113445nn b ⎛⎫=-- ⎪⎝⎭，求出11()i i i i n n E Y E Y b ==⎛⎫=∑=∑ ⎪⎝⎭，利用等比数列求和公式得到答案.【详解】（1）设第n 次传球后排球在甲、乙、丙、丁手中的概率分别为*,,,,n n n n a b c d n ∈N ，则11112120,,,555a b c d ====．第2次传球到乙手中的概率211212112455555525b c d =+=⨯+⨯=，所以第3次传球是由乙传给甲的概率为2285125b =．..........................................................4分（2）根据已知条件可得，当2n ≥时，111111111111212,555221,555212,555212,555n n n n n n n n n n n n n n n n a b c d b a c d c b a d d a b c ------------⎧=++⎪⎪⎪=++⎪⎨⎪=++⎪⎪⎪=++⎩①②③④联立则有()()11111,515n n n n n n n n a c a c b d b d ----⎧-=--⎪⎪⎨⎪-=--⎪⎩，所以{}n n a c -是首项为15-，公比为15-的等比数列，故15nn n a c ⎛⎫-=- ⎪⎝⎭．因为1125b d ==，所以n n b d =， 代入①②式得11111411,5552141,5555nn n n n n n n b c c b c b -----⎧⎛⎫=+--⎪ ⎪⎪⎝⎭⎨⎛⎫⎪=-++ ⎪⎪⎝⎭⎩⑤⑥， 将⑤代入⑥得113714445n n n n b c c -⎛⎫=+-- ⎪⎝⎭，11223615555n n n n c c c ---⎛⎫=+-- ⎪⎝⎭，则()1112336135555n n n n n c c c c n ----⎛⎫⎛⎫⎛⎫+-+=--≥ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，，其中211222555555252228b dc =+=⨯+⨯=，故211811252533555c c ⨯==++，2322133615555c c c c ⎛⎫⎛⎫⎛⎫+-+=-- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，3433233615555c c c c ⎛⎫⎛⎫⎛⎫+-+=-- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，……，111233615555n n n n n c c c c ----⎛⎫⎛⎫⎛⎫+-+=-- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，由累加法可得2211311611121525555555n nn n c c --⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫+=--+-++-=+-⎢⎥ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎢⎥⎣⎦ ， 所以1111131112545254n n n n c c --⎡⎤⎛⎫⎛⎫+--=-+--⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎣⎦，所以111254n n c ⎧⎫⎪⎪⎛⎫+--⎨⎬ ⎪⎝⎭⎪⎪⎩⎭是以111125c ⎛⎫+-- ⎪⎝⎭13420=-为首项，公比为35-的等比数列，所以1111342545n nn c ⎛⎫⎛⎫=--+- ⎪ ⎪⎝⎭⎝⎭，故第n 次传球后排球传到丙手中的概率为1111342545nnn c ⎛⎫⎛⎫=--+- ⎪ ⎪⎝⎭⎝⎭． (12)分（3）随机变量i Y 服从两点分布，设第i 次未传到乙手中的概率为()0i P Y =， 则排球第i 次传到乙手中的概率为()11i P Y ==-()0,1,2,,i i P Y b i n === ， 则11i i i i n nE Y b ==⎛⎫∑=∑ ⎪⎝⎭．由（2）知113714445nn n n b c c -⎛⎫=+-- ⎪⎝⎭111111333133711685165168516545n n n n n--⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=--+-+--+--- ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭113445n⎛⎫=-- ⎪⎝⎭， 其中1111333533353553585588515n in n i n +++=⎛⎫--- ⎪⎡⎤⎛⎫⎛⎫⎛⎫⎝⎭∑-==---=---⎢⎥ ⎪ ⎪ ⎪⎛⎫⎝⎭⎝⎭⎝⎭⎢⎥⎣⎦-- ⎪⎝⎭，所以11*11333()1,4454325i n i i i n nn E Y b n ==⎡⎤⎡⎤⎛⎫⎛⎫=∑=∑--=+--∈⎢⎥⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎢⎥⎣⎦⎣⎦N ．.........................................................17分【点睛】方法点睛：由递推公式求解通项公式，根据递推公式的特点选择合适的方法， （1）若()1n n a a f n +-=，采用累加法； （2）若()1n na f n a +=，采用累乘法； （3）若()11n n a pa q p +=+≠，可利用构造111n n q q a p a p p +⎛⎫+=+ ⎪--⎝⎭进行求解；数学第2页（共6页）数学第3页（共6页）学校__________________班级__________________姓名__________________准考证号__________________﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍密﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍封﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍线﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍请在各题目的答题区域内作答，超出黑色矩形边框限定区域的答案无效！2025届高三开学摸底考试卷数学·答题卡请在各题目的答题区域内作答，超出黑色矩形边框限定区域的答案无效！请在各题目的答题区域内作答，超出黑色矩形边框限定区域的答案无效！请在各题目的答题区域内作答，超出黑色矩形边框限定区域的答案无效！16．（15分）。

2024届新高三开学摸底考试卷（全国通用，新教材）化 学（考试时间：75分钟 试卷满分：100分）注意事项：1．答卷前，考生务必将自己的姓名、考生号等填写在答题卡和试卷指定位置上。

2．回答选择题时，选出每小题答案后，用铅笔把答题卡对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

回答非选择题时，将答案写在答题卡上。

写在本试卷上无效。

3．考试结束后，将本试卷和答题卡一并交回。

可能用到的相对原子质量：H 1 C 12 N 14 O 16 Sr 88 Cu 64 Ti 48第Ⅰ卷（选择题 共42分）一、选择题：本题共14个小题，每小题3分，共42分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．我国“嫦娥五号”成功携带月球样品返回地球。

下列有关说法错误的是A ．运载火箭使用煤油液氧推进剂，煤油是石油分馏产品，分馏属于物理变化B ．探测器装有太阳能电池板，能将太阳能转化为电能C ．返回器带回的月壤中含有32He ，它与地球上42He 的性质完全相同 D ．嫦娥五号中超声电机的心脏——压电陶瓷是一种无机非金属材料2．科学家利用氦核42He 撞击氮原子，发生反应：4141712181He N O H +→+，下列说法正确的是A ．4He 的质子数为2B ．153NH 的中子数为9C ．172O 和16O 互为同位素D ．22H 与12H 化学性质不同3．下列说法正确的是A ．NaCl 、HCl 的水溶液都能导电，NaCl 、HCl 属于离子化合物B ．CaC 2、CaCl 2都含有离子键和非极性共价键 C ．石油分馏、煤的干馏都属于物理变化D ．Na 2SiO 3和SiC 都属于无机非金属材料 4．下列图示或化学用语错误．．的是 A ．羟基的电子式：B ．H 2O 的VSEPR 模型：C ．Mn 2+的价电子的轨道表示式：D ．中子数为5的铍原子：94Be5．对乙酰氨基酚是感冒冲剂的有效成分，其结构简式如图所示。

2025届高三第一次校际联考化学试题第Ⅰ卷（注意事项：1．本试卷满分100分，时间75分钟。

2．答卷前，务必将答题卡上密封线内的各项目填写清楚。

3．回答选择题时，选出每小题答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其它答案标号。

回答非选择题时，将答案写在答题卡上。

写在本试卷上无效。

4．考试结束后，监考员将答题卡按顺序收回，装袋整理；试题不回收。

可能用到的相对原子质量：H-1 Li-7 Be-9 C-12N-14O-16选择题 共42分）一、选择题（本大题共14小题，每小题3分，计42分。

每小题只有一个选项符合题意）1．商朝青铜器双羊尊是中国青铜器的代表作品。

下列说法正确的是（ ） A ．青铜的熔点比纯铜高B ．青铜、黄铜和紫铜都是铜的同素异形体C ．青铜与稀硝酸共热，会产生NO 气体D ．青铜表面的铜绿的主要成分是碳酸铜2．下列过程的主要化学反应中一定涉及氧化还原反应的是（ ） A ．工业制玻璃B ．海水提溴C ．明矾净水D ．钟乳石的形成3．芯片是人类智慧的结晶。

晶体硅广泛用于制造芯片，Si 暴露在空气中表面会形成2SiO 薄膜。

下列说法错误的是（ ） A ．Si 晶体属于单质 B ．2SiO 属于氧化物 C ．Si 晶体属于共价晶体D ．2SiO 属于半导体4．三氯化六氨合钴()336Co NH Cl 是一种重要的化工产品，实验室可用反应()2342233262CoCl 10NH 2NH Cl H O 2Co NH Cl 2H O +++=+ 制备。

下列说法正确的是（ ）A ．2H O 的VSEPR 模型为B ．3NH 的电子式为C ．基态Cl 原子的价电子轨道表示式为D ．()3361mol Co NH +中含有18mol 共价键5．A N 为阿伏加德罗常数的值。

下列叙述正确的是（ ） A ．0.1mol 乙醇中含有极性共价键的数目为A 0.7NB ．“铯原子钟”中的铯原子为13355Cs ，则133550.2mol Cs 含有的中子数目为A 11N C ．常温常压下，46g 24N O 和2NO 的混合物中含有的原子总数为A 6N D ．标准状况下，2.24L 3NH 含有的孤电子对数目为A 0.4N 6．下列有关硫及其化合物的性质与用途具有对应关系的是（ ） A ．硫单质呈黄色，可用作橡胶硫化剂 B ．2SO 具有氧化性，可用于漂白草编织物 C ．浓硫酸具有强氧化性，可用作酯化反应的催化剂 D ．23Na SO 具有还原性，可用于处理自来水中残留的2Cl 7．下列实验的对应操作中，不合理的是（ ）A ．分离2I 和铁粉B ．用HCl 标准溶液滴定NaOH 溶液C ．测量2O 体积D ．收集2Cl8．某消毒液的主要成分为NaClO ，还含有一定量的NaCl 和NaOH 。

山东省济南市2025届高三上学期开学摸底考试数学试题一、单选题1．已知集合2{|340}M x x x =--<，{2,1,0,1,2,3}N =--，则M N ⋃=（ ） A ．{0,1,2,3}B ．{2,1,0,1,2,3}--C ．{|14x x -≤<或}2x =-D ．{|24}x x -<<2．若复数z 满足()12i 24i z +⋅=-，则z =（ ）A ．12B ． 2C ．2D ．43．已知向量(),3a k =r，()2,0b =r ，若()3a a b ⊥+r r r ，则k =（ ）A ．3-B ．−2C ．2D ．34．已知两条不同的直线,m n 和平面α，且n ⊂α，则“//m n ”是“//m α”的（ ） A ．充分不必要条件 B ．必要不充分条件 C ．充要条件D ．既不充分也不必要条件5．已知函数 ()()22ln 3=--+f x x ax a 在 [)1,+∞上单调递增，则a 的取值范围是（ ）A ．(],1-∞-B ．(),1∞--C ．(],2-∞D ．()2,+∞6．由0，1，2，3，4，5组成没有重复数字的六位数，其中任意两个偶数都不相邻，则满足条件的六位数的个数为（ ） A ．60B ．108C ．132D ．1447．直线22y x =-与曲线 si 11xy n x x π=+--的交点个数为（ ） A ．2B ．3C ．4D ．58．设12345x x x x x <<<<，随机变量1ξ取值12345,,,,x x x x x 的概率均为0.2，随机变量2ξ取值233445511222222,,,,33333x x x x x x x x x x +++++的概率也均为0.2，则（ ） A ．()()12E E ξξ> B ．()()12E E ξξ< C ．()()12D D ξξ>D ．()()12D D ξξ<二、多选题9．已知在某市的一次学情检测中，学生的数学成绩X 服从正态分布(100,100)N ，其中90分为及格线，120分为优秀线，下列说法正确的是（ ）附:随机变量ξ服从正态分布2~(,)N μσ，则()0.6826P μσξμσ-<<+=，(22)0.9544P μσξμσ-<<+=，(33)0.9974P μσξμσ-<<+=.A ．该市学生数学成绩的标准差为100B ．该市学生数学成绩的期望为100C ．该市学生数学成绩的及格率超过0.8D ．该市学生数学成绩不及格的人数和优秀的人数大致相等10．已知函数()3231f x x x ax a =-+-+，则（ ）A ．()f x 至少有一个零点B ．存在a ，使得()f x 有且仅有一个极值点C ．点()1,1-是曲线()y f x =的对称中心D ．当0a ≤时，()f x 在[]0,1上单调递减11．在平面直角坐标系xOy 中，已知点()1,0A -，()10B ,，直线AM ，BM 相交于点M ，且它们的斜率之和是2.设动点(),M x y 的轨迹为曲线C ，则（ ）A ．曲线C 关于原点对称B ．曲线C 关于某条直线对称C ．若曲线C 与直线y kx =（0k >）无交点，则1k ≥D ．在曲线C 上取两点(),P a b ，(),Q c d ，其中0a <，0c >，则2PQ >三、填空题12．已知双曲线()2222100x y C a b a b-=>>：，的一条渐近线的方程为20x y +=，则C 的离心率的值为. 13．曲线 1ln1xy x+=-在点()0,0处的切线方程为.14．数列 {}n a 满足[]2111,121n n a a a +∈-=-，，记 123n n T a a a α=L ，则 2025T 的最大值为.四、解答题15．在ABC V 中，内角A ，B ，C 所对的边分别为a ，b ，c ，已知 cos cos 3b C c B b c ++=. (1)求ABC V 的周长；(2)若sin sin2a B b A =，求△ABC 的面积.16．如图，在四棱锥P ABCD -中，PA ⊥底面ABCD ,AD CD =,2PA AC ==，AB BC =(1)证明：平面PAC ⊥平面PBD ；(2)若3BD =，求平面ADP 与平面BDP 的夹角的余弦值.17．在平面直角坐标系xOy 中，已知椭圆C 的两个焦点分别是()1F ，)20F ，点M 在C 上，且 124MF MF +=.(1)求C 的标准方程；(2)若直线y kx =C 交于A ，B 两点，且OAB △求k 的值. 18．已知函数()()1ln 1e x f x a x x +=+-.(1)当0a <时，求()f x 的单调区间； (2)若函数()f x 存在正零点0x ， （i ）求a 的取值范围；（ii ）记1x 为()f x 的极值点，证明：013x x <. 19．已知数列{}n a 为正项数列，数列{}n b 满足12nn a a a b n+++=L .(1)试写出一个数列{}n a ，使得{}n b 为递增的等差数列；(2)若{}n b 为递增的等差数列，从12,,,m a a a L 中任选一项，记为随机变量X .（i ）比较()k P X a ≥与mkb a 的大小关系，其中1,2,,k m =L ，并说明理由； （ii ）若()1D X =，证明：()124m P X b -≥<.。

2024—2025学年安徽省百师联盟高三上学期开学摸底联考物理试卷一、单选题(★★) 1. 如图所示，将塑料瓶下侧开一个小孔，瓶中灌入清水，水就从小孔流出。

将激光水平射向塑料瓶小孔，观察到激光束沿水流方向发生了弯曲，光被完全限制在水流内，这是光的（）A．干涉现象B．全反射现象C．衍射现象D．折射现象(★★) 2. 研究光电效应规律的电路图如图甲所示，某同学分别用a、b、c三束单色光照射光电管得到的光电流I与光电管两端电压U的关系如图乙所示。

已知a、c两条图线与横轴的交点重合。

下列说法正确的是（）A．a、c光的光强相同B．a、b光的频率相同C．用b光照射时，逸出光电子的最大初动能最大D．用a光、b光照射时，该光电管的截止频率不同(★★★) 3. 如图为某游乐场的圆弧形滑梯，表面粗糙。

小明将一个小球从最高处由静止释放，小球从最低处以某一速度滑离，关于上述过程的说法中一定正确的是（）A．小球受到滑梯的支持力大于它对滑梯的压力B．小球受到滑梯的力的方向始终与速度方向相反C．小球滑至最低处时受力平衡D．小球重力势能减少量大于动能增加量(★★★) 4. 如图所示，在离地一定高度处，一个沙漏水平向右做匀加速直线运动，沿途连续漏出沙子，若不计空气阻力，则沙子排成的形状为（）A．B．C．D．(★★) 5. 2024年6月4日，携带月球样品的嫦娥六号上升器自月球背面起飞，随后成功进入预定环月轨道，图为嫦娥六号着陆月球前部分轨道的简化示意图，Ⅰ是地月转移轨道，Ⅱ、Ⅲ是绕月球运行的椭圆轨道，Ⅳ是绕月球运行的圆形轨道。

P、Q分别为椭圆轨道Ⅱ的远月点和近月点。

已知圆轨道Ⅳ到月球表面的高度为h，月球半径为R，月球表面的重力加速度为g，不考虑月球的自转，嫦娥六号（）A．由轨道Ⅰ进入轨道Ⅱ，需在P处向后喷气B．在轨道Ⅳ上绕月运行的速度大小为C．在轨道Ⅳ上绕月运行的周期大于在轨道Ⅲ上绕月运行的周期D．在轨道Ⅱ上稳定运行时经过P点的加速度大于经过Q点的加速度(★★★) 6. 如图所示为风力发电机，其叶片转动时可形成半径为20m的圆面。