概率论与数理统计 常用的统计分布共61页文档
- 格式:ppt
- 大小:4.92 MB
- 文档页数:61


数理统计分布类型数理统计是数学和统计学的交叉学科,研究收集、整理、分析和解释数据的方法和原则。
其中,分布类型是数理统计的重要概念之一。
统计分布是指一组数据按照一定规律的分布情况,根据数据分布的形状和特点,可以将统计分布分为不同的类型。
常见的数理统计分布类型有正态分布、均匀分布、伯努利分布、二项分布、泊松分布、几何分布、指数分布、正态分布、t分布和F分布等。
以下将逐一介绍这些常见的分布类型。
1.正态分布:正态分布(或高斯分布)是数理统计中最常见的一种分布类型。
正态分布的密度函数呈钟形曲线,对称且具有峰值,其分布的均值、方差决定了曲线的位置和形状。
正态分布在自然界和社会现象中广泛存在,如身高、体重、考试成绩等。
2.均匀分布:均匀分布是指数据在给定区间内的分布是均匀的,即每个数据点出现的概率相等。
均匀分布的密度函数是一个常数,对应的分布函数是线性的。
均匀分布常用于模拟随机数产生、建立实验设计等领域。
3.伯努利分布:伯努利分布是一种离散型的分布,只有两个可能的取值(例如0和1),其中一个取值的概率为p,另一个取值的概率为1-p。
伯努利分布常用于描述二项式试验中的成功和失败的概率。
4.二项分布:二项分布是由多次独立的伯努利试验组成的概率分布,其中每个试验只有两个可能的结果(例如成功和失败)。
二项分布可以用于描述多次独立重复试验中成功次数的分布情况。
5.泊松分布:泊松分布是一种用于描述单位时间或空间内事件发生次数的概率分布。
泊松分布假设事件以恒定的平均速率独立地发生,其参数λ表示单位时间或空间内事件的平均发生次数。
6.几何分布:几何分布是一种描述第一次成功发生需要的独立试验次数的概率分布。
每次试验只有两个可能的结果(例如成功和失败),成功的概率为p,几何分布描述了第一次成功发生之前需要进行的试验次数的分布情况。
7.指数分布:指数分布是描述时间间隔或空间间隔的分布,它的特点是具有无记忆性。
指数分布可以用于描述等待时间、服务时间、设备故障时间等。


概率论与数理统计中的三种重要分布摘要:在概率论与数理统计课程中,我们研究了随机变量的分布,具体地研究了离散型随机变量的分布和连续型随机变量的分布,并简单的介绍了常见的离散型分布和连续型分布,其中二项分布、Poisson 分布、正态分布是概率论中三大重要的分布。
因此,在这篇文章中重点介绍二项分布、Poisson 分布和正态分布以及它们的性质、数学期望与方差,以此来进行一次比较完整的概率论分布的学习。
关键词:二项分布;Poisson 分布;正态分布;定义;性质一、二项分布二项分布是重要的离散型分布之一,它在理论上和应用上都占有很重要的地位,产生这种分布的重要现实源泉是所谓的伯努利试验。
(一)泊努利分布[Bernoulli distribution ] (两点分布、0-1分布)1.泊努利试验在许多实际问题中,我们感兴趣的是某事件A 是否发生。
例如在产品抽样检验中,关心的是抽到正品还是废品;掷硬币时,关心的是出现正面还是反面,等。
在这一类随机试验中,只有两个基本事件A 与A ,这种只有两种可能结果的随机试验称为伯努利试验。
为方便起见,在一次试验中,把出现A 称为“成功”,出现A 称为“失败” 通常记(),p A P = ()q p A P =-=1。
2.泊努利分布定义:在一次试验中,设p A P =)(,p q A P -==1)(,若以ξ记事件A 发生的次数,则⎪⎪⎭⎫⎝⎛ξp q 10~,称ξ服从参数为)10(<<p p 的Bernoulli 分布或两点分布,记为:),1(~p B ξ。
(二)二项分布[Binomial distribution]把一重Bernoulli 试验E 独立地重复地进行n 次得到n 重Bernoulli 试验。
定义:在n 重Bernoulli 试验中,设(),()1P A p P A q p ===-若以ξ记事件A 发生的次数,则ξ为一随机变量,且其可能取值为n ,,2,1,0 ,其对应的概率由二项分布给出:{}k n kk n p p C k P --==)1(ξ,n k ,,3,2,1,0 =,则称ξ服从参数为)10(,<<p p n 的二项分布,记为),(~p n B ξ。


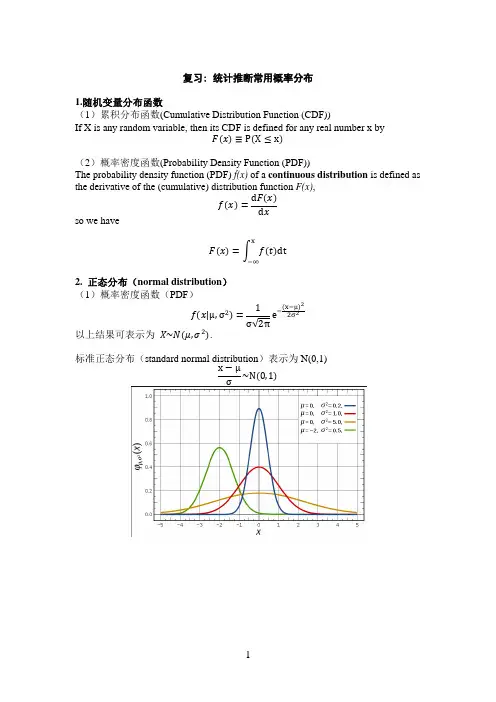
复习: 统计推断常用概率分布1.随机变量分布函数(1)累积分布函数(Cumulative Distribution Function (CDF))If X is any random variable, then its CDF is defined for any real number x byP X x(2)概率密度函数(Probability Density Function (PDF))The probability density function (PDF) f(x) of a continuous distribution is defined as the derivative of the (cumulative) distribution function F(x),ddso we havedt2. 正态分布(normal distribution ) (1)概率密度函数(PDF )|µ,σ1σ√2πeµ以上结果可表示为 ~ ,.标准正态分布(standard normal distribution )表示为N(0,1)x µ~N 0,1(2) 累积分布函数 (CDF)1σ√2πeµdt3. Chi-squared ( )分布如果Z1, Z2 ..., Z n是相互独立的随机变量,且都服从于N(0,1)分布,那么服从自由度(degree of freedom, df)为n的χ 分布,记为X~χ n . (1)PDF of χ(2)CDF of χ4. t-分布(student's t-distribution)设)n (~Y )1,0(N ~X 2χ和,且X 和Y 相互独立,则称随机变量n Y X T /=服从df. 为n 的t-分布,记为T ~ t(n)。
(1)PDF of t-distribution(2)CDF of t-distribution5. F-分布X和Y是相互独立的χ 分布随机变量,d.f分别为m和n,则称随机变量n/ Y m/XF=服从df.为 (m, n)的F-分布,且通常写为F~F(m,n)。



离散型1. 二项分布 Binomial distribution :binom二项分布指的是 N 重伯努利实验,记为 X ~ b(n,p) ,E(x)=np,Var(x)=np(1-p)pbinom(q,size,prob) , q 是特定取值, 比如 pbinom(8,20,0.2) 指第 8 次伯努利 实验的累计概率。
size 指总的实验次数, prob 指每次实验成功发生的概率dbinom(x,size,prob), x 同上面的 q 同含义。
dfunction() 对于离散分布来说结 果是特定值的概率,对连续变量来说是密度( Density )rbinom(n, size, prob) ,产生 n 个 b(size,prob) 的二项分布随机数qbinom(p, size, prob),quantile function 分位数函数。
分位数:若概率0<p<1,随机变量X 或它的概率分布的分位数Za 。
是指满足条件 p(X>Za)= a 的实数。
女口 t 分布的分位数表,自由度f=20和a =0.05时的分位数 为1.7247。
--这个定义指的是上侧a 分位数a 分位数:实数 a 满足 0 < a <1 时, a 分位数是使 P{X< x a }=F(x a )=a 的数 x a双侧a 分位数是使P{X<入1}=F(入1)=0.5 a 的数入1、使P{X> 入 2}=1-F(入 2)=0.5 a 的数 入 2。
qbinom 是上侧分位数,如 qbinom(0.95,100,0.2)=27, 指 27 之后P(x>=27)>=0.95 。
即对于 b(100,0.2) 为了达到 0.95 的概率至少需要 27 次重复 实验。
2. 负二项分布 negative binomial distribution 掷骰子,掷到一即视为成功。
则每次掷骰的成功率是 1/6 。
标准正态表标准文案标准文案标准文案标准文案标准文案标准文案标准文案T分布标准文案标准文案标准文案标准文案标准文案标准文案标准文案F分布P= 0.90标准文案标准文案P= 0.99标准文案标准文案标准文案标准文案标准文案标准文案标准文案Excel公式1.正态分布函数Excel计算正态分布时,使用NORMDIST函数,其格式如下:NORMDIST(a,μ,σ,累积)其中,“累积”:若为TRUE,则输出分布函数值,即P{X≤a};若为FALSE,则为概率密度函数值.示例:已知X服从正态分布,μ=600,σ=100,求P{X≤500}.输入公式NORMDIST(500, 600, 100, TRUE)得到的结果为0.158655,即P{X≤500}=0.158655.2、正态分布函数的反函数标准文案Excel计算正态分布函数的反函数使用NORMINV函数,格式如下:NORMINV(p,μ ,σ ),此公式计算a,使P{X ≤a}=p 3标准正态分布反函数=NORMSINV(0.975)3、t分布Excel计算t分布的值,采用TDIST函数,格式如下:TDIST(a,自由度,侧数)其中,“侧数”:指明分布为单侧或双侧:若为1,为单侧;此命令输出P{ T >a }若为2,为双侧.此命令输出P{ |T| >a}示例:设T服从自由度为24的t分布,求P(T>1.711).已知t=1.711,df=24,采用单侧,则T分布的值:TDIST(1.711,24,1)得到0.05,即P(T > 1.711)=0.05.4. t分布的反函数标准文案Excel使用TINV函数得到t分布的反函数,格式如下:TINV(α,自由度)输出T 分布的α / 2 分位点:t_α/2_(n)若求临界值tα(n),则使用公式=TINV(2*α, n)函数FDIST 的计算公式为FDIST=P( F>x ),5.F分布的反函数FINV(probability,deg_freedom1,deg_freedom2) 已知probability=P( F>x ),求x标准文案。