方程显著性的检验

显著性检验对所有自变量与因变量之间的直线回归关系的拟合程度，可以用统计量R2来度量，其公式如下：TSS(Total Sum of Squares)称为总平方和，其值为，体现了观测值y1,y2,…,y n总波动大小，认为是在执行回归分析之前响应变量中的固有变异性。

ESS(Explained Sum of Squares)称为回归平方和，是由于y与自变量x1,x2,…,x n的变化而引起的，其值为，体现了n个估计值的波动大小。

RSS(Residual Sum of Squares)称为残差平方和，其值为。

R2称为样本决定系数，对于多元回归方程，其样本决定系数为复决定系数或多重决定系数。

回归模型的显著性检验包括：①对整个回归方程的显著性检验；②对回归系数的显著性检验。

对整个回归方程的显著性检验的假设为“总体的决定系统ρ2为零”，这个零假设等价于“所有的总体回归系数都为零”，即：检验统计量为R2，最终检验统计量为F比值，计算公式为：F比值的意义实际上是“由回归解释的方差”与“不能解释的方差”之比。

检验回归方程是否显著的步骤如下。

第1步，做出假设。

备择假设H1:b1,b2,…,b k不同时为0。

第2步，在H0成立的条件下，计算统计量F。

第3步，查表得临界值。

对于假设H0，根据样本观测值计算统计量F，给定显著性水平α，查第一个自由度为k，第二个自由度为n-k-1的F分布表得临界值F(k,n-k-1)。

当F≥Fα(k,n-k-1)时，拒绝假设H0，则认为回归方程α显著成立；当F＜Fα(k,n-k-1)时，接受假设H0，则认为回归方程无显著意义。

对某个回归参数βi的显著性检验的零假设为：H0：βi=0，检验的最终统计量为：具体步骤如下。

(1)提出原假设H0:βi=0；备择假设H1:βi≠0。

(2)构造统计量，当βi=0成立时，统计量。

这里是的标准差，k为解释变量个数。

(3)给定显著性水平α，查自由度为n-k-1的t分布表，得临界值。

回归方程的显著性检验回归方程的显著性检验的目的是对回归方程拟合优度的检验。

F检验法是英国统计学家Fisher提出的，主要通过比较两组数据的方差S2，以确定他们的精密度是否有显著性差异。

回归方程显著性检验具体方法为：由于y的偏差是由两个因素造成的，一是x变化所引起反应在S回中，二是各种偶然因素干扰所致S残中。

将回归方程离差平方和S回同剩余离差平方和S残加以比较，应用F检验来分析两者之间的差别是否显著。

如果是显著的，两个变量之间存在线性关系；如果不显著，两个变量不存在线性相关关系。

n个观测值之间存在着差异，我们用观测值yi与其平均值的偏差平方和来表示这种差异程度，称其为总离差平方和，记为由于所以式中称为回归平方和，记为S回。

称为残差平方和，记为。

不难证明，最后一项。

因此S总＝S回＋S残上式表明，y的偏差是由两个因素造成的，一是x变化所引起，二是各种偶然因素干扰所致。

事实上，S回和S残可用下面更简单的关系式来计算。

具体检验可在方差分析表上进行。

这里要注意S回的自由度为1，S残的自由度为n－2，S总的自由度为n－1。

如果x与y有线性关系，则其中，F（1，n-2）表示第一自由度为1，第二自由度为n-2的分布。

在F表中显著性水平用表示，一般取0.10，0.05，0.01，1-表示检验的可靠程度。

在进行检验时，F值应大于F表中的临界值Fα。

若F<0.05(1,n-2)，则称x与y 没有明显的线性关系，若F0.05(1,n-2)<F<F0.01(1,n-2)，则称x与y有显著的线性关系；若F>F0.01(1,n-2)，则称x与y有十分显著的线性关系。

当x与y有显著的线性关系时，在表2-1-2的显著性栏中标以〝*〞；当x与y有十分显著的线性关系时，标以〝**〞。

所有计量经济学检验方法(全)计量经济学所有检验方法一、拟合优度检验 可决系数TSSRSSTSS ESS R -==12 TSS 为总离差平方和，ESS为回归平方和，RSS 为残差平方和该统计量用来测量样本回归线对样本观测值的拟合优度。

该统计量越接近于1，模型的拟合优度越高。

调整的可决系数)1/()1/(12----=n TSS k n RSS R 其中：n-k-1为残差平方和的自由度，n-1为总体平方和的自由度。

将残差平方和与总离差平方和分别除以各自的自由度，以剔除变量个数对拟合优度的影响。

二、方程的显著性检验(F 检验)方程的显著性检验，旨在对模型中被解释变量与解释变量之间的线性关系在总体上是否显著成立作出推断。

原假设与备择假设：H 0:β1=β2=β3=…βk =0 H 1:βj 不全为0 统计量)1/(/--=k n RSS kESS F 服从自由度为(k , n-k-1)的F分布，给定显著性水平α，可得到临界值Fα(k,n-k-1)，由样本求出统计量F的数值，通过F>Fα(k,n-k-1)或F≤Fα(k,n-k-1)来拒绝或接受原假设H，以判定原方程总体上的线性关系是否显著成立。

三、变量的显著性检验（t检验）对每个解释变量进行显著性检验，以决定是否作为解释变量被保留在模型中。

原假设与备择假设：H0：βi=0 （i=1,2…k）；H1：βi≠0给定显著性水平α，可得到临界值tα/2(n-k-1)，由样本求出统计量t的数值，通过|t|> tα/2(n-k-1) 或|t|≤tα/2(n-k-1)来拒绝或接受原假设H0，从而判定对应的解释变量是否应包括在模型中。

四、参数的置信区间参数的置信区间用来考察：在一次抽样中所估计的参数值离参数的真实值有多“近”。

统计量)1(~1ˆˆˆ----'--=k n t k n c S t iiii iiie e βββββ在(1-α)的置信水平下βi 的置信区间是( , ) ββααββi i t s t s ii-⨯+⨯22，其中，t α/2为显著性水平为α、自由度为n-k-1的临界值。

方程显著性的检验方程显著性可用方程的F比值(F比值＝回归平方和÷残差平方和)和复相关系数描述，当α等于0.05以下，方程的可靠程度的概率超过95％。

复相关系数r接近1较好，随着项数的引进多，R会自动增加，容易形成假象。

所以，α的可靠性比R高。

样本的预留检验，是用预留的样本值直观检验回归方程预报值的拟合精度。

如果这几批都与预报值相差很大，再预报其它值还有可靠性吗？三种检验方法各有优缺点。

通常，样本数少、试验误差大、检测不准是造成检验难过关的主要原因。

1.F统计值在建模时，F临界值是用于引入或剔除一个变量时的一种尺度。

临界值高，在引入方程时，将显著性好的变量引入。

剔除时，又可将引入方程的变量再次检验，将变得不显著的剔除，使方程处于优化状态。

引入和剔除的F临界值是怎样确定呢？选择α＝？时的F分布表，查该表的第N1列、第n-N1-1行的值，该值即为该表α＝？时的f临界值。

其中n为样本个数，N1为方程中引入的变量模式数。

当N1=1时，是引入一个变量，所得F临界值用于建模。

若是回归方程中引入了5个自变量或是其组合项，此时N1=5，所得的F临界是用于描述方程拟合得好与坏。

在方差分析中，回归平方和是由自变量X的变化引起的，它的大小反映了自变量X的重要程度。

剩余平方和是由试验误差以及其它为加控制的因素引起的它的大小反映了试验误差及其它因素对试验结果的影响。

平方和除自由度为均方，两个均方相除得F比值。

在不同的显著性水平α下，F临界值不一样。

F比值高于F临界值，表明在显著性水平α＝？时，回归方程显著。

F比值值高，则显著性水平好，此时的α是反映回归方程拟合的程度。

2.显著性水平α显著性水平α在统计检验中具有重要作用，α＝0.05，意味着回归方程的有效性为95％，α＝0.01，为99％的可靠性。

通常α＝0.01，为高度显著；α＝0.05，为一般显著；α＝0.10以上，方程可靠性大为下降。

3.复相关系数R衡量回归方程拟合优良性的一种指标是复相关系数，用R表示，｜R｜≤1，R的绝对值越大，说明拟合得越好。

§3 回归方程及回归系数的显著性检验１、回归方程的显著性检验(1) 回归平方和与剩余平方和建立回归方程以后, 回归效果如何呢因变量与自变量是否确实存在线性关系呢这是需要进行统计检验才能加以肯定或否定, 为此, 我们要进一步研究因变量取值的变化规律。

的每次取值是有波动的, 这种波动常称为变差, 每次观测值的变差大小, 常用该次观侧值与次观测值的平均值的差(称为离差)来表示, 而全部次观测值的总变差可由总的离差平方和,其中:称为回归平方和, 是回归值与均值之差的平方和, 它反映了自变量的变化所引起的的波动, 其自由度(为自变量的个数)。

称为剩余平方和(或称残差平方和), 是实测值与回归值之差的平方和, 它是由试验误差及其它因素引起的, 其自由度。

总的离差平方和的自由度为。

如果观测值给定, 则总的离差平方和是确定的, 即是确定的, 因此大则小, 反之, 小则大, 所以与都可用来衡量回归效果, 且回归平方和越大则线性回归效果越显著, 或者说剩余平方和越小回归效果越显著, 如果＝0, 则回归超平面过所有观测点; 如果大, 则线性回归效果不好。

(2) 复相关系数为检验总的回归效果, 人们也常引用无量纲指标,或,称为复相关系数。

因为回归平方和实际上是反映回归方程中全部自变量的“方差贡献”, 因此就是这种贡献在总回归平方和中所占的比例, 因此表示全部自变量与因变量的相关程度。

显然。

复相关系数越接近１, 回归效果就越好, 因此它可以作为检验总的回归效果的一个指标。

但应注意, 与回归方程中自变量的个数及观测组数有关, 当相对于并不很大时, 常有较大的值, 因此实际计算中应注意与的适当比例, 一般认为应取至少为的５到10倍为宜。

(3) 检验要检验与是否存在线性关系, 就是要检验假设,当假设成立时, 则与无线性关系, 否则认为线性关系显著。

检验假设应用统计量,这是两个方差之比, 它服从自由度为及的分布, 即,用此统计量可检验回归的总体效果。

回归方程的效果的检验1.方程显著性检验(F 检验)F 检验是以方差分析为基础,对回归总体线性关系是否显著的一种假设检验,是解释模型中被解释变量与所有解释变量之间的线性关系在总体上是否显著的方法利用F 统计量进行总体线性显著性检验的步骤如下:(1)提出关于P 个总体参数的假设H0:b0=b1=b2=…=bp=0(2)构造统计量(3)检验 给定显著性水平α,查F 分布表若F>F α,拒绝H0,表明回归总体有显著性关系.若F<F α,接受原假设,表明不存在线性关系2.参数显著性检验参数显著性检验,是对每个解释变量进行检验.如果解释变量对被解释变量的影响不显著,应从模型中删除,如果解释变量对被解释变量的影响显著,应保留在模型中.利用t 统计量进行参数显著性检验的步骤如下:(1)对总体参数提出假设:H0:bi=0(2)构造统计量:(3)检验 对给定α,若︱t ︱>t α /2,说明拒绝原假设；若︱t ︱<t α /2,则接受原假设.如果一次t 检验后,模型中存在多个不重要变量,一般是将t 值最小的变量删除掉,再重是(X`X)-1主对角线上第i+1个元素3、复相关系数和偏相关系数复相关系数R 是由ESS 和TSS 构造的统计量，用来表示回归方程对原有数据拟合程度的好坏，衡量作为一个整体的x1,x2,…,xp 与y 的线性关系的大小。

回归方程的拟合优度检验就是要检验样本数据点聚集在回归直线周围的密集程度，从而评价回归方程对样本数据的代表程度。

由判定系数R2来实现。

实际中，随着自变量个数的不断增加，必然会使得R2不断变化，于是出现的问题是，R2变化是由于数学习性决定的，还是确实是由于引入了好的变量进入方程而造成的。

因此在作拟合优度检验的判定时，一般采用调整的R2，以消除自变量的个数以及样本量的大小对R2的影响。

其它变量被固定后，计算任意两个变量之间的相关系数，这种相关系数称为偏相关系数。

常用显著性检验1.t检验适用于计量资料、正态分布、方差具有齐性的两组间小样本比较。

包括配对资料间、样本与均数间、两样本均数间比较三种，三者的计算公式不能混淆。

2.t'检验应用条件与t检验大致相同，但t′检验用于两组间方差不齐时，t′检验的计算公式实际上是方差不齐时t检验的校正公式。

3.U检验应用条件与t检验基本一致，只是当大样本时用U检验，而小样本时则用t检验，t检验可以代替U检验。

4.方差分析用于正态分布、方差齐性的多组间计量比较。

常见的有单因素分组的多样本均数比较及双因素分组的多个样本均数的比较，方差分析首先是比较各组间总的差异，如总差异有显著性，再进行组间的两两比较，组间比较用q检验或LST检验等。

5.X2检验是计数资料主要的显著性检验方法。

用于两个或多个百分比(率)的比较。

常见以下几种情况：四格表资料、配对资料、多于2行*2列资料及组内分组X2检验。

6.零反应检验用于计数资料。

是当实验组或对照组中出现概率为0或100％时，X2检验的一种特殊形式。

属于直接概率计算法。

7.符号检验、秩和检验和Ridit检验三者均属非参数统计方法，共同特点是简便、快捷、实用。

可用于各种非正态分布的资料、未知分布资料及半定量资料的分析。

其主要缺点是容易丢失数据中包含的信息。

所以凡是正态分布或可通过数据转换成正态分布者尽量不用这些方法。

8.Hotelling检验用于计量资料、正态分布、两组间多项指标的综合差异显著性检验。

计量经济学检验方法讨论计量经济学中的检验方法多种多样，而且在不同的假设前提之下，使用的检验统计量不同，在这里我论述几种比较常见的方法。

在讨论不同的检验之前，我们必须知道为什么要检验，到底检验什么？如果这个问题都不知道，那么我觉得我们很荒谬或者说是很模式化。

检验的含义是要确实因果关系，计量经济学的核心是要说因果关系是怎么样的。

那么如果两个东西之间没有什么因果联系，那么我们寻找的原因就不对。

那么这样的结果是没有什么意义的，或者说是意义不大的。

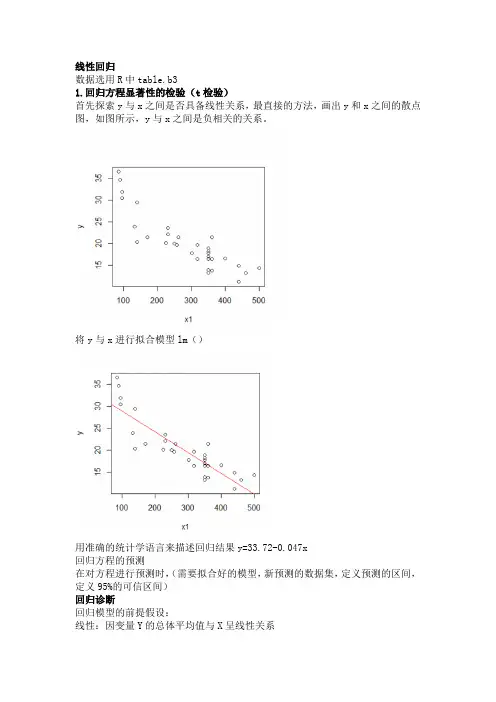
线性回归数据选用R中table.b31.回归方程显著性的检验（t检验）首先探索y与x之间是否具备线性关系，最直接的方法，画出y和x之间的散点图，如图所示，y与x之间是负相关的关系。

将y与x进行拟合模型lm（）用准确的统计学语言来描述回归结果y=33.72-0.047x回归方程的预测在对方程进行预测时，（需要拟合好的模型，新预测的数据集，定义预测的区间，定义95%的可信区间）回归诊断回归模型的前提假设：线性：因变量Y的总体平均值与X呈线性关系独立性：需要保证观测值之间是相互独立的正态性：线性模型的残差服从正态分布（残差毫无规律的分布在x=0的周围）等方差：不论X取什么值，Y都具有相同的方差出现情况：1.对于方差不齐的情况可以采用加权最小二乘法，对于距离较远的点赋予较小的权重，减少其不良影响。

2.共线性（拟合模型显著但自变量不显著）诊断方法方差膨胀因子，VIF>10有较强的共线性，VIF>100有严重的共线性，发现共线性的变量可剔除彼此共线性的变量2.高杠杆值（与离群点不同，其x值不在正常范围内）诊断方法（学生化残差，杠杆值，Cook距离）car包中的influencePlot函数找出该点外文文献总结一种基于模糊信息的乳腺癌危险因素方法评估目的：本篇文章是研究导致乳腺癌疾病的因素，研究发现有可控因素和不可控因素。

通过构建一个决策系统来观察导致乳腺癌的因素。

方法：通过BRFCM（基于规则的模糊认知图）方法来表示几种因素之间的属性和因果关系。

第一部分，利用基于模糊推理规则的方法，利用MATLAB（矩阵实验室）构造RBFCM的权重矩阵，得到了互连线的权重。

连接强度是根据这些因素的因果关系按权重值推断的。

第二部分通过模糊识别图评价影响BC发生的因素，并计算BC危险因素的影响程度。

第三部分，使用FCMapper软件分析结果。

在构建因果关系时，结合研究人员经验，来确定BRFCM的权重矩阵。

在FIS中的功能操作遵循以下四个步骤：评估每个规则的输入，获得每个规则的结论，汇总结论和去模糊化。

从统计学看线性回归（2）——⼀元线性回归⽅程的显著性检验⽬录1. σ2 的估计2. 回归⽅程的显著性检验 t 检验（回归系数的检验） F 检验（回归⽅程的检验） 相关系数的显著性检验 样本决定系数 三种检验的关系⼀、σ2 的估计 因为假设检验以及构造与回归模型有关的区间估计都需要σ2的估计量，所以先对σ2作估计。

通过残差平⽅和（误差平⽅和）（1）（⽤到和，其中）⼜∵（2）∴（3）其中为响应变量观测值的校正平⽅和。

残差平⽅和有n-2 个⾃由度，因为两个⾃由度与得到的估计值与相关。

（4）（公式（4）在《线性回归分析导论》附录C.3有证明）∴σ2的⽆偏估计量：（5）为残差均⽅，的平⽅根称为回归标准误差，与响应变量y 具有相同的单位。

因为σ2取决于残差平⽅和，所以任何对模型误差假设的违背或对模型形式的误设都可能严重破坏σ2的估计值的实⽤性。

因为由回归模型残差算得，称σ2的估计值是模型依赖的。

⼆、回归⽅程的显著性检验 ⽬的：检验是否真正描述了变量 y 与 x 之间的统计规律性。

假设：正态性假设（⽅便检验计算）1. t 检验 ⽤t 检验来检验回归系数的显著性。

采⽤的假设如下：原假设 H0：β1 = 0 （x 与 y 不存在线性关系）对⽴假设 H1：β1 ≠ 0 回归系数的显著性检验就是要检验⾃变量 x 对因变量 y 的影响程度是否显著。

下⾯我们分析接受和拒绝原假设的意义。

（1）接受 H0：β1 = 0 （x 与 y 不存在线性关系） 此时有两种情况，⼀种是⽆论 x 取值如何， y 都在⼀条⽔平线上下波动，即，如下图1，另⼀种情况为， x 与 y 之间存在关系，但不是线性关系，如图2。

图 1图 2 （2）拒绝 H0：β1 = 0 （x 对解释 y 的⽅差是有⽤的） 拒绝原假设也有两种情况，⼀种是直线模型就是合适的，如图 3，另⼀种情况为存在 x 对 y 的线性影响，也可通过 x 的⾼阶多项式得到更好的结果，如图 4。

二元选择模型的方程显著性检验
二元选择模型的方程显著性检验是用来判断整个模型的拟合优度是否显著。

在二元选择模型中，我们通常使用Logit模型或Probit模型来建模。

方程显著性检验是通过比较模型的似然比统计量（likelihood ratio，LR）与自由度的卡方分布来进行的。

具体步骤如下：
1. 假设：建立一个包含自变量的模型，假设自变量的系数都为零，也就是模型中只有截距项。

这个假设模型被称为“限制模型”。

2. 估计参数：对限制模型和完全模型（即包含自变量的模型）进行参数估计。

这里需要使用最大似然法进行参数估计。

3. 计算似然比统计量：分别计算限制模型的对数似然值（记为LR1）和完全模型的对数似然值（记为LR2），然后计算似然比统计量LR = 2 * (LR2 - LR1)。

4. 设置显著性水平：确定显著性水平（通常为0.05或0.01），用于判断似然比统计量是否显著。

5. 判断拟合优度：将似然比统计量与自由度为自变量个数的卡方分布进行比较。

如果似然比统计量大于卡方分布的临界值，则拒绝限制模型，接受完全模型。

需要注意的是，进行方程显著性检验时，要注意模型的合理性和严谨性，确保模型的拟合结果可靠。

回归方程的显著性检验： （1）在模型上做假设：建立回归方程的目的是寻找Y 的均值随a 的变化规律，即找出回归方程a Y 0=＋x a 11＋x a 22＋x a 33＋x a 44＋x a 55。

如果错误!未找到引用源。

=0,那么不管错误!未找到引用源。

如何变化，Y 不随a 的变化做任何改变，那么这时所求的回归方程是没有意义的。

，此时的回归方程是不显著的。

如果错误!未找到引用源。

，x x 51...≠0那么a 变化时，Y 随x 的作回归变化，那么这时求得的回归方程是有意义的，此时是显著地。

综上，对回归方程是否有意义作判断就要作如下的显著性检验：H：x x 51...全为0 H1：x x 51...不全为0拒绝错误!未找到引用源。

表示回归方程是显著的。

对最终求得的回归方程：x x x x Y 5421092.18833.19111.0363.026.574++-+-= 进行F 检验。

（2）找出统计量：数据总的波动用总偏差平方和用2131))((∑=-=i iyave ST y表示，引起各Yave 不同的原因主要有两个因素：其一是错误!未找到引用源。

可能不真，Y 随a 的变化而变化，从而在每一个a 的观测值处的回归值不同，其波动用回归平方和2131i yave ypre SR ∑=-=））（（表示，其二是其他一切因素，包括随机误差、a 对y 的非线性影响等，这样在得到回归值以后，y 的观测值与回归值之间还有差距，这可用残差平方和2131i iypre SE y ∑=-=））（（表示。

（3）F 值的计算由定理：设y 1321....y y ，错误!未找到引用源。

相互独立，且),...(~255110σx a x a a yi i iN +++，I = 1， (13)则在上述记号下，有 ①）（1n ~SE 22-χσ②若H 0成立，则有）（p ~SE22χσ，（p 为回归参数的个数） ③SR 与SE ，yave 独立。

显著性检验T检验零假设，也称稻草人假设，如果零假设为真，就没有必要把X纳入模型，因此如果X确定属于模型，则拒绝零假设Ho，接受备择假设H1，(Ho:B2=0 H1：B2≠0)假设检验的显著性检验法:t=（b2-B2）/Se(b2)服从自由度为（n-2）的t分布，如果令Ho:B2=B2*,B2*是B2的某个数值(若B2*=0)则t=（b2-B2*）/Se(b2)=（估计量—假设值）/假设量的标准误。

可计算出的t值作为检验统计量，它服从自由度为（n-2）的t分布，相应的检验过程称为t检验。

T检验时需知：①，对于双变量模型，自由度为（n-2）；②,在检验分析中，常用的显著水平α有1%，5%或10%，为避免选择显著水平的随意性，通常求出p值，p值充分小，拒绝零假设；③可用半边或双边检验。

双边T检验：若计算的ItI超过临界t值，则拒绝零假设。

显著性水平临界值t0.01 3.3550.05 2.3060.10 1.860单边检验：用于B2系数为正，假设为Ho:B2<=0, H1：B2>0显著性水平临界值t0.01 2.8360.05 1.8600.10 1.397F检验（多变量）（联合检验）F=[R2/(k-1)]/(1-R2)(n-k)=[ESS(k-1)]/RSS(n-k).n为观察值的个数，k 为包括截距在内的解释变量的个数，ESS(解释平方和)= ∑y^i2RSS(残差平方和)= ∑ei2TSS(总平方和)= ∑yi2=ESS+RSS.判定系数r2=ESS/TSSF与R2同方向变动，当R2=0（Y与解释变量X不想关），F为0，R2值越大，F值也越大，当R2取极限值1时，F值趋于无穷大。

F检验（用于度量总体回归直线的显著性）也可用于检验R2的显著性—R2是否显著不为0，即检验零假设式(Ho:B2=B3=0)与检验零假设R2为0是等价的。

虚拟变量虚拟变量即定性变量，通常表明具备或不具备某种性质，虚拟变量用D表示。

关于显著性检验，你想要的都在这⼉了！！（基础篇）⽆论你从事何种领域的科学研究还是统计调查，显著性检验作为判断两个乃⾄多个数据集之间是否存在差异的⽅法被⼴泛应⽤于各个科研领域。

笔者作为科研界⼀名新⼈也曾经在显著性检验⽅⾯吃过许多苦头。

后来醉⼼于统计理论半载有余才摸到显著性检验的⽪⽑，也为显著性检验理论之精妙，品种之繁多，逻辑之严谨所折服。

在此，特写下这篇博⽂，以供那些仍然挣扎在显著性检验泥潭的⾮统计专业的科研界同僚们参考。

由于笔者本⼈也并⾮统计专业毕业，所持观点粗陋浅鄙，贻笑⼤⽅之处还望诸位业界前辈，领域翘楚不吝赐教。

⼩可在此谢过诸位看官了。

本篇博⽂致⼒于解决⼀下⼏点问题，在此罗列出来：1.什么是显著性检验？ 2.为什么要做显著性检验？ 3.怎么做显著性检验？下⾯就请跟随笔者的步伐⼀步步⾛⼊显著性检验的“前世与今⽣”。

⼀：显著性检验前传：什么是显著性检验？它与统计假设检验有什么关系？为什么要做显著性检验？“显著性检验”实际上是英⽂significance test的汉语译名。

在统计学中，显著性检验是“统计假设检验”（Statistical hypothesis testing）的⼀种，显著性检验是⽤于检测科学实验中实验组与对照组之间是否有差异以及差异是否显著的办法。

实际上，了解显著性检验的“宗门背景”（统计假设检验）更有助于⼀个科研新⼿理解显著性检验。

“统计假设检验”这⼀正名实际上指出了“显著性检验”的前提条件是“统计假设”，换⾔之“⽆假设，不检验”。

任何⼈在使⽤显著性检验之前必须在⼼⾥明⽩⾃⼰的科研假设是什么，否则显著性检验就是“⽔中⽉，镜中花”，可望⽽不可即。

⽤更通俗的话来说就是要先对科研数据做⼀个假设，然后⽤检验来检查假设对不对。

⼀般⽽⾔，把要检验的假设称之为原假设，记为H0；把与H0相对应（相反）的假设称之为备择假设，记为H1。

如果原假设为真，⽽检验的结论却劝你放弃原假设。

此时，我们把这种错误称之为第⼀类错误。