数学简易逻辑 知识点+题型

第一章集合与简易逻辑第一节集合题型1、元素与集合的关系元素与集合的关系：属于和不属于。

常用数集的表示：C —复数集；R —实数集；Q —有理数集；Z —整数集；N —自然数集；N+或N*—正整数集。

1、【多选】下列关系中正确的是（）A.{}102，∉-B.(){}2|42x y x =∈，C.R ∈πD.Φ∈02、【2022·全国乙卷】设集合{}54321，，，，=U ，集合M 满足{}31，=M C U ，则（）A.M ∈2B.M ∈3C.M ∉4D.M∉53、【2018·北京】已知集合(){}241|≤-+≥-=ay x y ax y x y x A ，＞，，，则（）A ．()A R a ∈∈∀12，，B ．()AR a ∉∈∀12，，C ．当且仅当0＜a 时，()A ∉12，D ．当且仅当23≤a 时，()A ∉12，4、若集合{}2024||≤∈=x N x x P ，45=a ，则（）A.P a ∈B.{}P a ∈C.{}Pa ⊆D.Pa ∉题型2、集合相等集合元素的特征：确定性、互异性、无序性。

集合相等，集合中元素完全相同，集合中元素之和相等，集合中元素之积相等。

1、若},,0{},,1{2b a a ab a +=，求20242024b a+的值.【答案：1】2、已知集合，，且B A },,0{B },,,{A ==-=y x y x xy x 求实数x 与y 的值.【答案：x=y=-1】3、设R b a ∈,,集合b}ab {0a}b a {1，，，，=+,则=-a b （）【答案：C 】A.1B.-1C.2D.-24、【2014·福建】若}2,1,0{},,{=c b a ，且下列三个关系：①2≠a ；②2=b ；③0≠c 有且只有一个正确，求c b a ++10100的值.5、集合},2,0{a A =，},1{2a B =.若}16,4,210{，，=B A 则a 的值为（）【答案：D 】A ．0B ．1C ．2D ．4题型3、集合之间的基本关系集合与集合之间的关系：①包含关系，②相等关系，③真子集关系。

原命题若p 则q 否命题若┐p 则┐q逆命题若q 则p逆否命题若┐q 则┐p互为逆否互逆否互为逆否互互逆否互文科数学选修1—1 第一章 简易逻辑 一．四种命题及关系1。

命题:__________的语句；2。

分类：①简单命题：不含有逻辑联结词的命题;②复合命题：由_________和逻辑联结词“___”、“___"、“____”构成的命题；构成复合命题的形式：p 或q 记作______；p 且q 记作____；非p 记作_____。

3。

命题的四种形式与相互关系 原命题：若p 则q ； 逆命题：________； 否命题:________; 逆否命题:________.注:①互为_____关系的两个命题同真假．②命题中一些关键词的否定：1、下列说法：①若一个命题的否命题是真命题，则这个命题不一定是真命题;②若一个命题的逆否命题是真命题，则这个命题是真命题；③若一个命题的逆命题是真命题，则这个命题不一定是真命题；④若一个命题的逆命题和否命题都是真命题，则这个命题一定是真命题；其中正确的说法是 ( ）A 。

①②B 。

①③④C 。

②③④D 。

①②③2、已知m ，n 是两条不同的直线，α,β是两个不同的平面,则下列命题正确的是（ ） A 、若α，β垂直于同一个平面，则α//β B 、若m,n 平行于同一个平面,则m//nC 、若α，β不平行，则α内不存在与β平行的直线D 、若m,n 不平行，则m 与n 不可能垂直于同一个平面3．原命题：“设a ，b ，c ∈R ，若a 〉b ，则ac 2〉bc 2"，在原命题以及它的逆命题、否命题、逆否命题中，真命题的个数为( ）4．有四个命题：①“若0x y +=，则x 、y 互为相反数"的逆命题； ②“全等三角形的面积相等”的否命题;③“若1q ≤,则关于x 的方程220x x q ++=有实根"的逆命题；④“A B B =,则A B ⊇”的逆否命题。

20 道数学逻辑推理题目一、数字推理题1. 找规律填数字：2，4，6，8，（）。

-答案：10。

规律是后一个数比前一个数大2。

2. 1，3，7，15，（）。

-答案：31。

规律是后一个数比前一个数依次多2、4、8、16。

3. 2，5，11，23，（）。

-答案：47。

规律是后一个数比前一个数依次多3、6、12、24。

4. 3，6，9，12，（）。

-答案：15。

规律是后一个数比前一个数大3。

5. 4，8，16，32，（）。

-答案：64。

规律是后一个数是前一个数的2 倍。

二、图形推理题1. 观察图形：○△□，△□○，□○△，下一个图形是什么？-答案：○△□。

规律是三个图形依次循环。

2. 有一组图形，第一个是正方形，第二个是圆形，第三个是三角形，第四个是正方形，第五个是圆形，那么第六个图形是什么？-答案：三角形。

规律是正方形、圆形、三角形依次循环。

3. 观察图形序列：△△△△△△△△△，下一个图形是什么？-答案：△。

规律是△后面的△依次增加一个。

4. 一组图形为：△○□，□△○，○□△，下一组图形是什么？-答案：△○□。

规律是三个图形依次循环换位。

5. 图形序列：△△△△△△△△△，下一个图形是什么？-答案：△。

规律是△后面的△依次增加一个。

三、逻辑推理题1. 小明、小红、小刚三人中，一人是医生，一人是教师，一人是警察。

已知小明不是医生，小红不是教师，小刚不是警察。

那么小明是（），小红是（），小刚是（）。

-答案：教师、警察、医生。

通过排除法推理得出。

2. 桌子上有三个盒子，一个盒子里装着糖，一个盒子里装着饼干，一个盒子里装着糖和饼干。

三个盒子上分别贴着标签：A 盒“糖”，B 盒“饼干”，C 盒“糖和饼干”。

但标签都贴错了。

现在从一个盒子里取出一个物品，如果是糖，那么这个盒子里实际装着什么？-答案：糖和饼干。

因为标签都贴错了，如果从贴着“糖”标签的盒子里取出糖，那么这个盒子实际装着糖和饼干。

3. 甲、乙、丙三人参加跑步比赛，甲说：“我不是第一名。

简易逻辑精选练习题一、选择题1. “21=m ”是“直线03)2()2(013)2(=-++-=+++y m x m my x m 与直线相互垂直”的（ ）A ．充分必要条件B ．充分而不必要条件C ．必要而不充分条件D ．既不充分也不必要条件 2. 设集合A ＝｛x |11+-x x ＜0}，B ＝｛x || x －1|＜a }，若“a ＝1”是“A ∩B ≠”的（ ） A ．充分不必要条件 B ．必要不充分条件C ．充要条件D ．既不充分又不必要条件3. 命题p ：“有些三角形是等腰三角形”，则┐p 是（ ）A ．有些三角形不是等腰三角形B ．所有三角形是等腰三角形C ．所有三角形不是等腰三角形D ．所有三角形是等腰三角形4. 设命题p ：方程2310x x +-=的两根符号不同；命题q ：方程2310x x +-=的两根之和为3，判断命题“p ⌝”、“q ⌝”、“p q ∧”、“p q ∨”为假命题的个数为( )A ．0B ．1C ．2D ．35.“a ＞b ＞0”是“ab ＜222b a +”的 ( ) A ．充分而不必要条件 B ．必要而不充分条件C ．充要条件D ．既不充分也不必要条件6. 若不等式|x －1| <a 成立的充分条件是0<x <4,则实数a 的取值范围是 ( )A ．a ≤1B ．a ≤3C ．a ≥1D ．a ≥37. 下列命题中，其“非”是真命题的是（ ）A ．∀x ∈R ，x ²-22x + 2 ≥ 0B ．∃x ∈R ，3x-5 = 0C ．一切分数都是有理数D ．对于任意的实数a,b,方程ax=b 都有唯一解8. 0a <是方程2210ax x ++=至少有一个负数根的（ ） A ．必要不充分条件B ．充分不必要条件C ．充分必要条件D ．既不充分也不必要条件二、填空题9. （1）命题：,R x ∈∃ x 2＋x ＋1＜0的否定是 ，（2） 命题“∀x ∈R ，x 2-x +3>0”的否定是 ，（3） 命题 “对任意的x ∈{x|-2<x<4},|x-2|<3”的否定形式（4）命题 “∀x ，y ∈R ,有x ²+ y ² ≥ 0”的否定是（5） 命题 “不等式x 2+x -6>0的解是x <-3或x >2”的逆否命题是（6）命题“∀a ，b ∈R ，如果ab ＞0，则a ＞0”的否命题是（7）命题 “△ABC 中,若∠C=90°,则∠A 、∠B 都是锐角”的否命题为: ，否定形式： 。

专题：简易逻辑常见重难点题型※题型讲练【例1】写出命题“若x ≥2且y ≥3，则x ＋y ≥5”的逆命题、否命题、逆否命题，并判断其真假．变式训练1：1．写出命题“若△ABC 不是等腰三角形，则它的任何两个内角不相等.”的逆命题、否命题、逆否命题，并判断其真假．【例2】写出下列命题的“非P ”命题，并判断其真假： (1)若21,20m x x m >-+=则方程有实数根． (2)平方和为0的两个实数都为0．(3)若0abc =，则,,a b c 中至少有一为0．(4)若ABC ∆是锐角三角形， 则ABC ∆的任何一个内角是锐角． (5)若0)2)(1(=--x x ，则21≠≠x x 且 ．(6)91()AB ∈（其中全集*U N =，{}|A x x =是质数，{}|B x x =是正奇数）.变式训练2：1．已知命题“存在实数x 0，y 0，使得x 0＋y 0>1”. (1)用符号表示为 ；(2)此命题的否定是 (用符号表示)，是________(填“真”或“假”)命题．【例3】已知命题p ：存在实数x ，使sin x ＝π2成立；命题q ：x 2－3x ＋2＜0的解集为(1，2)．给出下列四个结论： ①命题“p ∧q ”是真命题； ②命题“p ∧￢p ”是假命题； ③命题“￢p ∧q ”是真命题； ④命题“￢p ∨￢q ”是假命题． 其中正确的结论是( )A ．②③B ．②④C ．①②④D ．①②③④变式训练3：1．如果命题“非p 或非q ”是假命题，给出下列四个结论： ①命题“p 且q ”是真命题； ②命题“p 且q ”是假命题； ③命题“p 或q ”是真命题； ④命题“p 或q ”是假命题． 其中正确的结论是( ) A ．①③ B ．②④ C ．②③D ．①④【例4】用合适的序号填空：①充分不必要 ②必要不充分 ③充要 ④既不充分也不必要 (1)p q ∨为真命题是p q ∧为真命题的 条件；(2):23A x -<, 是2:4150B x x --<的 条件； (3)设集合M={x | x ＞2}，P={x |x ＜3}，那么“x ∈M ，或x ∈P”是“x ∈M∩P”的 条件；(4)若a ＝(x,3)(x ∈R )，则“x ＝4”是“|a |＝5”的 条件； (5)“tan θ≠1”是“θ≠π4”的的 条件；(6)“cos A ＝2sin B sin C ”是“△ABC 为钝角三角形”的 条件； (7)“a n ＋1＞|a n |(n ＝1,2，…)”是“{a n }为递增数列”的 条件； (8)已知p 是q 的必要条件，r 是q 的充分条件，p 是r 的充分条件，那么q 是p 的 条件；【例5】已知命题p ：∃x ∈R ，mx 2＋1≤0，命题q ：∀x ∈R ，x 2＋mx ＋1>0.若“p ∨q ”的否定为真命题，求实数m 的取值范围．变式训练4：1．已知p ：∀x ∈R,2x >m (x 2＋1)，q ：∃x 0∈R ，x 20＋2x 0－m －1＝0，且p ∧q 为真，求实数m 的取值范围．【例6】已知命题p ：关于x 的函数y ＝x 2－3ax ＋4在[1，＋∞)上是增函数，命题q ：函数y ＝(2a －1)x 为减函数，若“p 且q ”为真命题，求实数a 的取值范围．变式训练5：1．设命题p ：实数x 满足x 2－4ax ＋3a 2<0，其中a >0，命题q ：实数x 满足⎩⎨⎧x 2－x －6≤0，x 2＋2x －8>0.(1)若a ＝1，且p ∧q 为真，求实数x 的取值范围；(2)非p 是非q 的充分不必要条件，求实数a 的取值范围．※课后练习1．下列命题中的假命题是()A．∀a，b∈R，a n＝an＋b，有{a n}是等差数列B．∃x0∈(－∞，0)，2x0<3x0C．∀x∈R,3x≠0D．∃x0∈R，lg x0＝02．与命题“若a∈M，则b∉M”等价的命题是() A．若a∉M，则b∉M B．若b∉M，则a∈M C．若a∉M，则b∈M D．若b∈M，则a∉M 3．下列命题中正确的是()A．若p∨q为真命题，则p∧q为真命题B．“x＝5”是“x2－4x－5＝0”的充分不必要条件C．命题“若x<－1，则x2－2x－3>0”的否定为：“若x≥－1，则x2－2x－3≤0”D．命题p：∃x∈R，x2＋x－1<0，则非p：∃x∈R，x2＋x－1≥0 4．下列说法错误的是()A．如果命题“非p”与命题“p或q”都是真命题，那么命题q一定是真命题B．命题“若a＝0，则ab＝0”的否命题是：若“a≠0，则ab≠0”C．若命题p：∃x0∈R，ln(x20＋1)<0，则非p：∀x∈R，ln(x2＋1)≥0D．“sin θ＝12”是“θ＝30°”的充分不必要条件5．已知命题p：“∀x∈[0,1]，a≥e x”，命题q：“∃x∈R，x2＋4x ＋a＝0”，若命题“p∧q”是真命题，则实数a的取值范围是() A．(4，＋∞) B．[1,4] C．[e,4] D．(－∞，1] 6．设f(x)是R上的减函数，且f(0)＝3，f(3)＝－1，设P＝{x||f(x ＋t)－1|<2}，Q＝{x|f(x)<－1}，若“x∈P”是“x∈Q”的充分不必要条件，则实数t的取值范围是()A．t≤0 B．t≥0 C．t≤－3 D．t≥－3 7．命题“∃x<0，有x2>0”的否定是______________．8．“lg x>lg y”是“10x>10y”的条件．9．下列结论：①若命题p：∃x0∈R，tan x0＝2；命题q：∀x∈R，x2－x＋1 2>0.则命题“p∧(綈q)”是假命题；②已知直线l1：ax＋3y－1＝0，l2：x＋by＋1＝0，则l1⊥l2的充要条件是ab＝－3；③“设a、b∈R，若ab≥2，则a2＋b2>4”的否命题为：“设a、b∈R，若ab<2，则a2＋b2≤4”．其中正确结论的序号为________．(把正确结论的序号都填上)10．设a，b，c为△ABC的三边，求证：方程x2＋2ax＋b2＝0与x2＋2cx－b2＝0有公共根的充要条件是∠A＝90°. 11．已知命题p：|x2－x|≥6; q：x∈Z，若“p∧q”与“非q”同时为假命题，求x的值．12．已知命题p：∃x∈R,2x2－3ax＋9<0.(1)写出非p：；(2)若非p为真命题，求实数a的取值范围．13．已知命题p：关于x的不等式x4－x2＋1x2>m的解集为{x|x≠0，x∈R}；命题q：f(x)＝－(5－2m)x是减函数．若“p∨q”为真命题，“p∧q”为假命题，求实数m的取值范围.。

数学逻辑推理题目
逻辑推理题目一直是数学领域中的重要内容，它要求我们通过严密的推理和分
析来解决问题。

今天我将给大家提供一些数学逻辑推理题目，希望能够帮助大家提升逻辑推理能力。

1. 题目一：有三个罐子，分别标有"A"、"B"、"C"，其中一个罐子里装有红球，另外两个罐子里各有一个白球。

现在一个人随机选择一个罐子，从中抽取一球，结果是红球。

问：这个红球来自哪个罐子的概率最大？
2. 题目二：有两个箱子，一个标有"苹果"，另一个标有"橙子"。

实际情况是，
标有"苹果"的箱子里有苹果和橙子，标有"橙子"的箱子里只有橙子。

现在随机选择
一个箱子，从中抽取一个水果，结果是苹果。

问：这个水果来自哪个箱子的概率最大？
3. 题目三：有两个人，一个总是说真话，另一个总是说谎话。

现在你遇到了一
个人，他说他是说真话的那个人，问：他到底是说真话的人还是说谎话的人？
以上是三道数学逻辑推理题目，希望大家可以认真思考，分析问题，找到合适
的解决方法。

逻辑推理是一种重要的思维方式，通过不断练习和思考，可以提升我们的逻辑思维能力，帮助我们更好地解决问题。

希望大家能够善用逻辑推理，解决更多有趣的问题。

全国高考数学试题分类解析——简单逻辑1.(安徽理科第7题）命题“所有能被2整除的数都是偶数”的否定．．是（ ） （A ）所有不能被2整除的数都是偶数（B ）所有能被2整除的数都不是偶数（C ）存在一个不能被2整除的数是偶数（D ）存在一个不能被2整除的数不是偶数解析：全称命题的否定是特称命题，选D2.（北京文科第4题）若p 是真命题，q 是假命题，则（ ）（A ）p q ∧是真命题 (B)p q ∨是假命题(C)p ⌝是真命题 (D)q ⌝是真命题答案: D3.（福建理科第2题）若R a ∈，则2=a 是0)2)(1(=--a a 的（ ）A.充分而不必要条件 B 必要而不充分条件C.充要条件D.既不充分又不必要条件答案：A4.（福建文科3）若a ∈R ，则“a=1”是“|a|=1”的（ ）A. 充分而不必要条件B. 必要而不充分条件C. 充要条件D. 既不充分又不必要条件答案：A5.（湖北理科9、文科10）若实数b a ,满足0,0≥≥b a ，且0=ab ，则称a 与b 互补，记()b a b a b a --+=22,ϕ，那么()0,=b a ϕ是a 与b 互补（ ）A. 必要而不充分条件B. 充分而不必要条件C. 充要条件D. 既不充分也不必要的条件 答案：C解析：若实数b a ,满足0,0≥≥b a ，且0=ab ，则a 与b 至少有一个为0，不妨设0=b ，则()0,2=-=-=a a a a b a ϕ，反之，若()0,22=--+=b a b a b a ϕ 则022≥+=+b a b a ，两边平方得ab b a b a 22222++=+0=⇔ab ，则a 与b 互补，故选C.6.（湖南理科2）设{1,2}M =，2{}N a =，则“1a =”是“N M ⊆”则（ ）A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分又不必要条件答案：A解析：因“1a =”，即{1}N =，满足“N M ⊆”，反之“N M ⊆”，则2{}={1}N a =，或2{}={2}N a =，不一定有“1a =”。

简单的数学逻辑题简介：数学逻辑题是一种通过推理关系和运用逻辑思维解决问题的数学题目。

本文将介绍一些简单的数学逻辑题，并提供解题方法和技巧，帮助读者更好地理解和应用数学逻辑。

1. 数列题数列是一组按照一定规律排列的数字的集合。

解决数列题的关键在于找出数列中的规律，从而确定下一个数字。

例如，给定数列1, 2, 4, 7, 11，要求找出下一个数字。

解析：观察数列，可以发现每个数字与前一个数字之间的差均递增1，即2-1=1，4-2=2，7-4=3，11-7=4。

因此，下一个数字应为11+5=16。

2. 排列组合题排列组合是数学中研究对象选择与排列的方法。

解决排列组合题的关键在于确定选择的规则和计算的方法。

例如，有5个不同的颜色的球，从中选择3个球的不同组合有多少种？解析：根据排列组合的公式，计算选择3个球的不同组合数为：C(5, 3) = 5! / (3! * (5-3)!) = 10。

因此，有10种不同的组合方式。

3. 图形推理题图形推理题是一种通过观察图形之间的相似性和变化规律来确定下一个图形的题目。

解决图形推理题的关键在于找出图形之间的规律和变化方式。

例如，给定下面的图形序列，请找出下一个图形。

解析：观察图形，可以发现每个图形在下一个图形中都增加了一圈小圆点，并且旋转了一定角度。

因此，下一个图形应为四个小圆点组成的正方形，并旋转一定角度。

4. 逻辑推理题逻辑推理题是一种通过分析前提条件和推理规则来确定结论的题目。

解决逻辑推理题的关键在于理清思路，找出逻辑关系和推理规律。

例如，给定以下命题：- 如果今天下雨，那么路会湿。

- 路不湿。

请问今天是否下雨？解析：根据第一个命题，如果下雨，则路会湿。

根据第二个命题，路不湿。

根据逻辑推理，如果前提条件成立，那么结论也应成立。

即，如果路不湿，那么今天没有下雨。

结论：数学逻辑题是一种训练逻辑思维和推理能力的有效方法。

通过多练习和掌握解题技巧，可以更好地理解和应用数学逻辑。

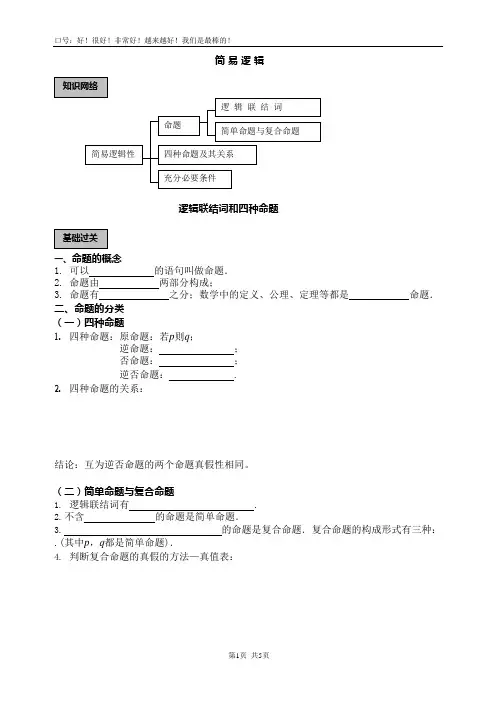
简 易 逻 辑逻辑联结词和四种命题一、命题的概念1. 可以 的语句叫做命题．2. 命题由 两部分构成；3. 命题有 之分；数学中的定义、公理、定理等都是 命题．二、命题的分类 （一）四种命题1. 四种命题：原命题：若p 则q ；逆命题： ； 否命题： ； 逆否命题： .2. 四种命题的关系：结论：互为逆否命题的两个命题真假性相同。

（二）简单命题与复合命题 1. 逻辑联结词有 . 2. 不含 的命题是简单命题． 3. 的命题是复合命题．复合命题的构成形式有三种： .(其中p ，q 都是简单命题)．4. 判断复合命题的真假的方法—真值表：(三)全称命题与存在命题1.全称量词：，用表示；2.存在量词：，用表示。

3.全称命题：，；4. 存在命题：，。

三、区分“命题的否定”和“否命题”1.命题的否定只否定结论：；2.否命题条件、结论都否定：。

例1. 分别写出下列命题的逆命题、否命题、逆否命题，并判断它们的真假:(1) 若q<1，则方程x2＋2x＋q＝0有实根；(2) 若ab＝0，则a＝0或b＝0；(3) 若x2＋y2＝0，则x、y全为零.变式训练：写出下列命题的否命题，并判断原命题及否命题的真假：（1）如果一个三角形的三条边都相等，那么这个三角形的三个角都相等；（2）矩形的对角线互相平分且相等；（3）相似三角形一定是全等三角形.例2：如果命题“p或q”是真命题，“p且q”是假命题.那么（）A.命题p和命题q都是假命题B.命题p和命题q都是真命题C．命题p和命题“非q”真值不同D．命题q和命题p的真值不同变式训练：下列结论中正确的是（）（A）命题p是真命题时，命题“P且q”一定是真命题。

（B）命题“P且q”是真命题时，命题P一定是真命题（C）命题“P且q”是假命题时，命题P一定是假命题（D）命题P是假命题时，命题“P且q”不一定是假命题例3.已知p：x2 +mx + 1 = 0 有两个不等的负根，q：4x2 + 4(m - 2)x + 1 = 0 无实根．若p或q为真，p且q 为假，求m的取值范围．分析：由p或q为真，知p、q必有其一为真，由p且q为假，知p、q必有一个为假，所以，“p假且q真”或“p真且q假”.可先求出命题p及命题q为真的条件，再分类讨论．变式训练：已知下列三个方程：①x2＋4ax－4a＋3＝0，②x2＋(a－1)x＋a2＝0，③x2＋2 ax－2a＝0中至少有一个方程有实根，求实数a的取值范围.充要条件p ⇒q 则p 叫做q 的 条件，q 叫做p 的条件． 2. 必要条件：如果q ⇒ p 则p 叫做q 的 条件，q 叫做p 的条件．p ⇒q 且q ⇒ p 则p 叫做q 的条件．例1：下列“若p ，则q ”形式的命题中，哪些命题中的 p 是q 的充分条件？（1）若x = 1，则x 2 - 4x + 3 = 0;（2） 若f (x ) = x ，则 f ( x )为增函数; （3） 若x 为无理数,则x 2为无理数.例2：下列“若p ，则q ”形式的命题中，哪些命题中的q 是p 的必要条件？（1） 若x = y ，则x 2 = y 2 ;（2） 若两个三角形全等，则这两个三角形的面积相等;(3) 若a > b ,则ac > bc .例3．在下列各题中，判断A 是B 的什么条件，并说明理由． 1． A ： p ≥ 2, p ∈ R ，B ：方程 x 2 + px + p + 3 = 0 有实根； 2．A ： 2x - 3 > 1 ；B ：1x 2+ x - 6> 0 ；变式训练：指出下列命题中，p 是q 的什么条件（在“充分不必要条件”、“必要不充分条件”、“充要条件”、“既不充分也不必要条件”中选出一种作答）. （1） 对于实数x 、y ，p ：x+y≠8,q:x≠2或y≠6; （2） 非空集合A 、B 中，p ：x∈A∪B，q ：x∈B； 例4.已知p ：－2＜m ＜0，0＜n ＜1；q ：关于x 的方程x 2＋mx ＋n ＝0有两个小于1的正根，试分析p 是q 的什么条件.变式训练：证明一元二次方程ax 2+bx+c=0有一正根和一负根的充要条件是ac<0.简易逻辑章节测试题一、选择题1. 下列语句中是命题的是（ ） （A ）语文和数学 （B ）sin45°=1 (C)x 2+2x-1 （D ）集合与元素2. 已知下列三个命题 1 方程x 2-x+2=0的判别式小于或等于零；②矩形的对角线互相垂直且平分；③2是质数，其中真命题是（）（A）①和②（B）①和③（C）②和③（D）只有①3.下列结论中正确的是（）（A）命题p是真命题时，命题“P且q”一定是真命题。

高考数学总复习题型分类汇《集合与简易逻辑》篇经典试题大汇总目录【题型归纳】题型一集合的交并补运算 (3)题型二集合的交并补与不等式结合 (3)题型三四种命题的基本考查 (4)题型四充要条件的判断 (4)【巩固训练】题型一集合的交并补运算 (5)题型二集合的交并补与不等式结合 (5)题型三四种命题的基本考查 (6)题型四充要条件的判断 (6)高考数学《集合与简易逻辑》题型归纳与训练【题型归纳】题型一 集合的交并补运算例1 ：已知集合{0,2}=A ，{21012}=--，，，，B ，则A B =（ ）A ．{0,2}B ．{1,2}C ．{0}D ．{21012}--，，，， 【答案】A【解析】由题意{0,2}A B =，故选A ．【易错点】交并不分 【思维点拨】概念的应用例2已知集合{}1,3,5,7A =，{}2,3,4,5B =，则AB =（ ）A ．{3}B ．{5}C ．{3,5}D ．{}1,2,3,4,5,7【答案】C【解析】因为{}1,3,5,7A =，{}2,3,4,5B =，所以{3,5}A B =，故选C ． 【易错点】交并不分 【思维点拨】概念的应用题型二 集合的交并补与不等式结合例3：已知集合{|2}A x x =<，{320}B x =->，则（ ）A ．3{|}2AB x x =< B ．A B =∅C ．3{|}2A B x x =< D ．A B =R【答案】A【解析】∵3{|}2B x x =<，∴3{|}2A B x x =<， 选A ．【易错点】不等式解错【思维点拨】掌握常规不等式的解答例4：设集合2{|}M x x x ==，{|lg 0}N x x =≤，则MN =( )A ．[0，1]B ．(0，1]C ．[0，1)D ．(－∞，1] 【答案】A【解析】∵{0,1}M =，{|01}N x x ≤=<，∴M N =[0,1]．【易错点】方程解错，对数不等式不会解答【思维点拨】基本函数和方程思想的掌握题型三 四种命题的基本考查例5：设m R ∈，命题“若0m >，则方程20x x m +-=有实根”的逆否命题是A ．若方程20x x m +-=有实根，则0m >B ．若方程20x x m +-=有实根，则0m ≤C ．若方程20x x m +-=没有实根，则0m >D ．若方程20x x m +-=没有实根，则0m ≤ 【答案】D【解析】一个命题的逆否命题，要将原命题的条件、结论加以否定，并且加以互换，故选D ． 【易错点】概念混淆【思维点拨】加强对四种命题的强化题型四 充要条件的判断例6：设x ∈R ，则“38x >”是“||2x >” 的（ ）A ．充分而不必要条件B ．必要而不充分条件C ．充要条件D ．既不充分也不必要条件 【答案】A【解析】由38x >，得2x >，由||2x >，得2x >或2x <-，故“38x >”是“||2x >” 的充分而不必要条件，故选A ． 【易错点】解不等式【思维点拨】加强部分不等式的解答例7：设a ，b ，c ，d 是非零实数，则“ad bc =”是“a ，b ，c ，d 成等比数列”的（ ）A ．充分而不必要条件B ．必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件【答案】B【解析】a ，b ，c ，d 是非零实数，若ad bc =，则b da c=，此时a ，b ，c ，d 不一定成等比数列；反之，若a ，b ，c ，d 成等比数列，则a cb d=，所以ad bc =，所以“ad bc =”是“a ，b ，c ，d 成等比数列”的必要而不充分条件．故选B ．【易错点】等比数列的概念遗忘导致 【思维点拨】对其他部分知识的熟悉度要高【巩固训练】题型一 集合的交并补运算1.已知全集{1,2,3,4,5}U =，{1,3}A =，则)(=A C U A ．∅ B ．{1，3} C ．{2，4，5} D ．{1，2，3，4，5}【答案】C【解析】【解析】因为{1,2,3,4,5}U =，{1,3}A =，所以=UA {2，4，5}．故选C ．2.设集合{1,2,3}A =，{2,3,4}B =则AB =( )A ．{1,2,3,4}B ．{1,2,3}C ．{2,3,4}D ．{1,3,4} 【答案】A【解析】由并集的概念可知，{1,2,3,4}AB =，选A ．3.设集合{1,2,6}A =，{2,4}B =，{1,2,3,4}C =，则()A B C =( )A ．{2}B ．{1,2,4}C ．{1,2,4,6}D ．{1,2,3,4,6} 【答案】B 【解析】∵{1,2,4,6}AB =，(){1,2,4}A BC =，选B ．题型二 集合的交并补与不等式结合1.设集合{}11M x x =-<，{}2N x x =<，则M N =( )A ．()1,1-B ．()1,2-C ．()0,2D ．()1,2【答案】C【解析】{|02}M x x =<<，所以{|02}MN x x =<<，选C ．2.已知集合{123}A =，，，2{|9}B x x =<，则()A B =A ．{210123}--，，，，，B ．{21012}--，，，，C ．{123}，，D ．{12}， 【答案】D【解析】易知{|33}B x x =-<<，又{1,2,3}A =，所以{1,2}A B =故选D ．3.已知集合A ={x |2230x x --≥}，B ={x |－2≤x ＜2}，则AB =( )A ．[-2, -1]B ．[-1,1]C ．[-1,2）D ．[1,2） 【答案】A【解析】{}|13A x x x =-≤或≥，故AB =[-2, -1]．题型三 四种命题的基本考查1.命题“若4πα=，则tan 1α=”的逆否命题是( )A ．若4πα≠，则tan 1α≠ B ．若4πα=，则tan 1α≠C ．若tan 1α≠，则4πα≠ D ．若tan 1α≠，则4πα=【答案】C【解析】因为“若p ，则q ”的逆否命题为“若p ⌝，则q ⌝”，所以 “若4πα=，则tan 1α=”的逆否命题是 “若tan 1α≠，则4πα≠”．2. ）已知,,a b c R ∈，命题“若a b c ++=3，则222a b c ++≥3”，的否命题是( )A ．若3a b c ++≠，则222a b c ++<3B ．若3a b c ++=，则222a b c ++<3C ．若3a b c ++≠，则222a b c ++≥3D ．若222a b c ++≥3，则3a b c ++=【答案】A【解析】3a b c ++=的否定是3a b c ++≠，222a b c ++≥3的否定是222a b c ++<3，故选A ． 3.设,a b 是向量，命题“若=-a b ，则=a b ”的逆命题是（ ）A ．若≠a b ，则≠a bB ．若=-a b ，则≠a bC ．若≠a b ，则≠a bD ．若=a b ，则=-a b【答案】D【解析】根据定义若“若a b =，则a b =-”．题型四 充要条件的判断1.设,a b ∈R ，“0a =”是‘复数i a b +是纯虚数”的( )A ．充分而不必要条件B ．必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件 【答案】B【解析】0a =时i a b +不一定是纯虚数，但i a b +是纯虚数0a =一定成立，故“0a =”是“复数i a b +是纯虚数”的必要而不充分条件．2. “ϕπ=”是“曲线()sin 2y x ϕ=+过坐标原点的”( )A ．充分而不必要条件B ．必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件【答案】A【解析】当ϕπ=时，sin 2y x =-过原点；()sin 2y x ϕ=+过原点，则,,0,,ϕππ=⋅⋅⋅-⋅⋅⋅等无数个值．选A ．3.设p ：3x <，q ：13x -<<，则p 是q 成立的( ) A ．充分必要条件 B ．充分不必要条件 C ．必要不充分条件 D ．既不充分也不必要条件 【答案】C【解析】∵(1,3)(,3)-⊆-∞，所以p 是q 成立的必要不充分条件．与现形课标对比，必修3中的“算法初步”删掉了；删掉了必修5中的解三角形，不等式的大部分内容。

一年级小学生的简单数学逻辑题随着学习的深入，数学逻辑逐渐成为小学生们学习数学的一部分。

在一年级，老师会给学生们布置一些简单的数学逻辑题，以培养他们思维能力和逻辑推理能力。

本文将为大家介绍一些适合一年级小学生的简单数学逻辑题，帮助他们培养逻辑思维和解决问题的能力。

问题一：数数图案请数一数，图案中共有几个圆圈？图1:O O OOO O O图2:O OO O图3:O O OO O OO O O解题思路：学生需要观察每个图案中的圆圈数量，并进行逐个数数。

通过观察和计数，学生可以发现图1有6个圆圈，图2有4个圆圈，而图3有9个圆圈。

问题二：找规律请找出每组图案中的规律，并根据规律填写问号处的数字。

图4:1 2 34 ? 67 8 9图5:2 4 68 ? 1214 16 ?解题思路：学生需要观察每个图案中数字的排列规律，并尝试在问号处填写符合规律的数字。

通过观察，学生可以发现图4中每行数字递增1，而第二行的中间数字为5。

因此，问号处的数字应为5。

同理，图5中每行数字递增2，第三行的第三个数字为18。

因此，问号处的数字应为18。

问题三：找不同请找出每组图案中与其他图案不同的一项，并将其编号写在括号内。

图6:⚪️⚪️⚪️⚪️⚪️⚪️⚪️⚪️⚪️图7:⚪️⚪️⚪️⚪️⚪️⚪️⚪️⚪️⚪️图8:⚪️⚪️⚪️⚪️⚪️⚪️⚪️⚪️⚪️解题思路：学生需要仔细观察每个图案中的不同之处，并将不同的图案进行编号。

通过观察，学生可以发现图6中所有的圆点都是白色，而图7中第一行最后一个圆点颜色不同。

因此，图7是与其他图案不同的一项。

通过这些简单的数学逻辑题，一年级小学生可以培养观察和思考的能力，提高他们的数学思维和解决问题的能力。

教师可以通过这些题目来引导学生进行思考和讨论，激发他们对数学的兴趣。

同时，家长们也可以在家陪伴孩子一起解决这些问题，帮助他们提高数学逻辑思维能力。

总结：数学逻辑题对于一年级小学生来说是一种很好的学习方式，可以培养他们的观察力、思考力和解决问题的能力。

数学中的逻辑思维训练逻辑题目集锦逻辑思维是数学中非常重要的一项能力。

通过解答逻辑题目，我们可以培养和锻炼自己的逻辑思维能力，提高数学解题的准确性和速度。

本文将为大家汇总一些数学中的逻辑题目，帮助读者提升逻辑思维能力。

题目一：数列逻辑给定数列：1, 2, 4, 7, 11, 16, 22, 29, 37, ...请问下一个数是多少？题目二：集合逻辑已知集合A = {1, 2, 3, 4, 5}，集合B = {4, 5, 6, 7, 8}。

求A∩B的结果。

题目三：关系逻辑已知关系R = {(1, 1), (2, 1), (3, 2), (4, 3), (4, 4), (5, 4), (6, 5)}，定义在集合S = {1, 2, 3, 4, 5, 6}上。

请问R是否是集合S上的等价关系？若是，请判断R的等价类，若否，请说明原因。

题目四：推理逻辑有5个人，他们分别是A、B、C、D、E。

已知以下条件：1. A和E两人是好朋友；2. B和C两人是兄弟姐妹；3. C和D两人是好朋友，但与B没有任何关系；4. D和E两人互不认识。

请问，谁是D的血亲关系最亲密的人？题目五：概率逻辑某班级有30名学生，其中20人会拉小提琴，15人会弹钢琴，10人两样都会。

现随机选取一名学生，请问他即不会拉小提琴也不会弹钢琴的概率是多少？以上就是本文提供的一些数学中的逻辑题目。

希望通过这些题目的解答，能够帮助读者加强自己的逻辑思维训练，并对数学解题有更深刻的理解。

当然，逻辑思维的培养需要长期的训练和实践，希望大家能够坚持下去，不断提高自己的数学能力。

一、选择题1.若一个四位数的千位数字与个位数字之和为10，且这个四位数加上3968后仍为四位数，并且新四位数的数字顺序与原四位数的数字顺序完全颠倒，则原四位数是？A.1089B.1980（答案）C.9801D.89102.甲乙丙丁四人进行象棋比赛，每两人之间都要赛一盘。

规定：胜一盘得2分，平一盘各得1分，输一盘不得分。

甲乙丙共得10分，丁得多少分？A.2分B.3分C.4分D.6分（答案）3.有一栋居民楼，每家都订了2份不同的报纸，该居民楼共订了三种报纸，其中，中国电视报34份，北京晚报30份，参考消息22份，那么订北京晚报和参考消息的共有多少家？A.12家B.14家C.16家D.18家（答案）4.甲、乙、丙、丁四人同时参加全国小学数学夏令营。

赛前甲、乙、丙分别做了预测。

甲说：“丙第5名，我第3名。

”乙说：“我第1名，丁第4名。

”丙说：“丁第2名，我第3名。

”成绩揭晓后，发现他们每人只说对了一半，你能说出他们的名次吗？A.甲第1名，乙第2名，丙第5名，丁第4名B.甲第3名，乙第1名，丙第4名，丁第2名（答案）C.甲第3名，乙第4名，丙第5名，丁第2名D.甲第4名，乙第2名，丙第3名，丁第1名5.有100枚1元的硬币，其中有一枚是假的，假的比真的轻，现在有一台天平，请问：最少称几次，就一定可以把假的硬币找出来？A.7次B.8次C.9次D.10次（答案）6.某商店规定3个空瓶可以换1瓶汽水，某班同学买了100瓶汽水，最多能喝到多少瓶汽水？A.132瓶B.133瓶（答案）C.134瓶D.140瓶7.一个正方形的内部有1996个点，以正方形的4个顶点和内部的1996个点为顶点，将它剪成一些三角形。

问：一共可以剪成多少个三角形？如果沿上述这些点中某两点之间所连的线段剪开算作一刀，那么共需剪多少刀？A.3994个三角形，6000刀B.3994个三角形，5988刀（答案）C.3992个三角形，6000刀D.3992个三角形，5988刀8.已知六个连续奇数的和是888，则这六个数中最小的数是？A.141B.143（答案）C.145D.147。

数学经典的20道逻辑题好的，下面我将列举一些经典的数学逻辑题，希望能够满足你的需求。

1. 有一条绳子，燃烧需要60分钟，但不一定均匀。

如何用这条绳子计时45分钟？2. 有三个开关分别控制三盏灯，但你在房间外，只能进去一次。

如何知道哪个开关控制哪盏灯？3. 有8个球，其中7个重量相同，1个重量略有不同。

用天平称两次，如何找出重量略有不同的那个球？4. 有一个8升和一个5升的水罐，如何用它们得到4升水？5. 一辆火车长1英里，正以60英里/小时的速度行驶。

一只飞蛾在火车头以120英里/小时的速度飞行。

飞蛾从火车头飞到尾部需要多长时间？6. 有一堆硬币，其中有一枚是假币，但你不知道假币比真币轻还是重。

用天平最少称几次可以找出假币？7. 有一张长方形的纸，折叠一次后的长度是10厘米，宽度是10厘米。

请问这张纸原本的长和宽各是多少？8. 有一根绳子，燃烧需要60分钟。

现在有若干根这样的绳子，请问如何用它们计时15分钟？9. 有一堆砖，每块砖重1磅加半块砖的重量。

请问这堆砖一共有多少块？10. 一个数加上100是一个完全平方数，再加上168又是一个完全平方数，这个数是多少？11. 有一个正方形的花坛，每条边上都有一棵树，相邻两棵树的距离是10米。

请问这个花坛的面积是多少？12. 一家商店的一只铁锅重8磅，里面装满了水，总重量是12磅。

如果这只铁锅是空的，它的重量是多少？13. 有一堆苹果，分给A、B、C三人。

A拿走1/2个，B拿走1/3个，C拿走1/4个，最后还剩下8个。

请问开始有多少个苹果？14. 有一个3升的容器和一个5升的容器，如何用它们得到4升水？15. 一个正方形花坛的对角线长10米，求花坛的面积。

16. 有一堆砖，每块砖重3/4磅。

请问这堆砖一共有多少块？17. 有一堆砖，每块砖重1/3磅。

请问这堆砖一共有多少块？18. 有一堆砖，每块砖重1/5磅。

请问这堆砖一共有多少块？19. 有一堆砖，每块砖重2/3磅。

逻辑基本题型总结1. 排列组合题型排列组合题型是逻辑题中常见的一种题型，主要测试考生对不同元素之间关系的分析能力。

常见的排列组合题型包括全排列、部分排列、组合等。

全排列全排列题型要求考生将一组元素按照一定规则进行排列，要求考生找出所有可能的排列方式。

解这类题目时，可以采用递归的方法，不断进行元素的交换和移动，直到找到所有的排列方式。

部分排列部分排列题型要求考生从一组元素中选出部分元素进行排列，要求考生找出所有可能的部分排列方式。

解这类题目时，可以采用递归的方法，不断进行元素的选择和移动，直到找到所有的部分排列方式。

组合组合题型要求考生从一组元素中选出若干个元素进行组合，要求考生找出所有可能的组合方式。

解这类题目时，可以采用递归的方法，不断进行元素的选择和移动，直到找到所有的组合方式。

2. 数字推理题型数字推理题型是逻辑题中涉及到数字和数学运算的题型，主要测试考生的数学与逻辑思维能力。

常见的数字推理题型包括数列推理、数学运算等。

数列推理数列推理题型要求考生根据已给出的数列，找出其中的规律并推理出下一个数或缺失的数。

解这类题目时，可以采用观察规律、列出算式或构造递推公式等方法。

数学运算数学运算题型要求考生进行一系列的数学运算，解出给定的问题。

解这类题目时，可以采用根据题目设定的数学关系进行变量代入、列方程式或运用数学定理等方法。

3. 逻辑推理题型逻辑推理题型是逻辑题中考察考生逻辑思维和推理能力的题型，主要测试考生理解、推断和判断的能力。

常见的逻辑推理题型包括条件推理、演绎推理等。

条件推理条件推理题型要求考生根据给出的条件和规则，推断出相应的结论。

解这类题目时，可以采用画逻辑图、列真值表或使用推理规则等方法。

演绎推理演绎推理题型要求考生根据给出的命题，进行推理和判断。

解这类题目时，可以采用推理规则、逻辑公式或使用真假推断等方法。

以上是逻辑基本题型的总结，希望对您的复习有所帮助。

祝您考试顺利！。

简易逻辑1．已知命题:(0,),32x x p x ∀∈+∞>；命题:(,0),32q x x x ∃∈-∞>,则下列命题为真命题的是（ ）． A ． p q ∧ B ．(q)p ∧⌝ C ．()p q ⌝∧ D ． ()()p q ⌝∧⌝2.“1m n >>”是 “log 2log 2m n <”的（ ）．A ．充分而不必要条件B ．必要而不充分条件C ． 充分必要条件D ．既不充分也不必要条件 3.在ABC △中，π4A =，BC“AC =”是“π3B =”的（ ） A ．充分不必要条件 B ．必要不充分条件C ． 充要条件D ．既不充分也不必要条件4． “8m <”是“方程221108x y m m -=--表示双曲线”的（ ）．A ．充分而不必要条件B ．必要而不充分条件C ．充分必要条件C ． 既不充分也不必要条件5．等比数列{}n a 中，10a >，则“13a a <”是“36a a <”的（ ）A ．充分而不必要条件B ．必要而不充分条件C ．充分必要条件 C ． 既不充分也不必要条件1.【答案】B【解析】解：因为命题p 是真命题，命题q 是假命题，所以()p q ∧⌝是真命题 故选B2.【答案】A【解析】解：因为1m n >> ，则22log log 0m n >>，所以2211log log m n<． 即“1m n >>”⇒“log 2log 2m n <” 另一方面，若log 2log 20m n <<，即22110log log m n<<，所以22log log 0n m <<，则1n m <<即“log 2log 2m n <”推不出“1m n >>”．所以“1m n >>”是 “log 2log 2m n <”充分不必要条件． 故答案选A ．3.答案】B【解析】解：若AC=，π4A=，BC=，由正弦定理得sinsinAC ABBC⋅==又(0,π)B∈，则π3B=或2π3．所以“AC=”推不出“π3B=”；另一方面，若π4A=，BCπ3B=，则sinsinBC BACA⋅===所以“π3B=”能推出“AC．所以“AC”是“π3B=”的必要不充分条件．故选B4．【答案】A【解析】解：若方程221108x ym m-=--表示双曲线，则当焦点在x轴时．2210080m am b⎧-=>⎪⎨-=>⎪⎩．，解得10m>；当焦点在y轴时2210080m bm a⎧-=-<⎪⎨-=-<⎪⎩解得8m<；所以“8m<”能推出“方程表示双曲线”而不能反推故答案为A．5.【答案】B【解析】解：如果13a a<，则211a a q<∴21q>，若1q<-，则231a a q=>，561a a q=<∴36a a>，∴“13a a<”不是“36a a<”的充分条件；如果36a a<成立，则2511a q a q<，又1a>，∴31q<∴1q >， ∴2113a a q a <=，故可判断，“13a a <”是“36a a <”的必要条件． 综上，“13a a <”是“36a a <”必要而不充分条件． 故选B ．。

数学逻辑推理题题目一：异或运算在二进制数中，异或运算符（^）用于比较两个位是否相同，如果相同则返回0，不同则返回1。

请你计算以下两个十进制整数的异或结果。

数a：255数b：1023解答：我们可以将两个十进制数转换为二进制数，然后逐位进行异或运算。

数a的二进制表示为11111111，数b的二进制表示为1111111111。

我们逐位进行异或运算：1.第一位：1 ^ 1 = 02.第二位：1 ^ 1 = 03.第三位：1 ^ 1 = 04.第四位：1 ^ 1 = 05.第五位：1 ^ 1 = 06.第六位：1 ^ 1 = 07.第七位：1 ^ 1 = 08.第八位：1 ^ 1 = 09.第九位：1 ^ 1 = 010.第十位：1 ^ 1 = 0因此，数a和数b的异或结果为0。

题目二：逻辑门电路逻辑门电路是计算机中常用的基本组件，用于实现逻辑运算。

以下是一个由两个逻辑门组成的电路，请你计算输入电压为0、1时，输出电压是多少。

逻辑门1为与门（AND gate），逻辑门2为或门（OR gate）。

Logic GatesLogic Gates解答：我们来逐个计算输入电压为0、1时，输出电压的情况。

当输入电压为0时，通过与门的输入线路可以得知，两个输入信号都为0，根据与门的运算规则，输出电压为0。

由于与门和或门之间是串联连接的，因此输出电压同样为0。

当输入电压为1时，通过与门的输入线路可以得知，两个输入信号都为1，根据与门的运算规则，输出电压为1。

由于与门和或门之间是串联连接的，因此输出电压同样为1。

因此，当输入电压为0和1时，输出电压分别为0和1。

题目三：数学推理现在有三个正整数a、b、c满足以下条件：1. a + b = 102. b - c = 2请你推导出满足以上条件的a、b、c的具体值。

解答：根据条件1，我们可以得到方程a + b = 10。

由于a和b是正整数，我们可以列举出一些满足条件的可能组合：1 + 9 = 102 + 8 = 103 + 7 = 104 + 6 = 105 + 5 = 106 + 4 = 107 + 3 = 108 + 2 = 109 + 1 = 10然后根据条件2，我们可以得到方程b - c = 2。