当前位置：文档之家 › 第2章 流体静力学 [全部]

第2章 流体静力学 [全部]

  • 格式：pdf
  • 大小：1022.35 KB
  • 文档页数：17

下载文档原格式

  / 17

合集下载

工程流体力学第2章流体静力学

工程流体力学第2章流体静力学

① 沿任意方向 ② 沿外法线方向
有切向分力 流体受拉力
都将破坏流体平衡。
这与静止前提不符，故假设不成立，则原命题成立。
①
②
4
第2章 流体静力学
特性二、静止流体中任何一点上各个方向的静压力大小相等，与作用面方位无关。
证明：采用微元体分析法 ① 取微单元体
在静止流体中，在O点附近取出各边长分别 为dx、dy、dz的微小四面体OABC。相应坐标 轴为x、y、z。
第2章 流体静力学
流体静力学：研究流体在静止状态下的平衡规律及其应用。 静止：流体质点相对于参考系没有运动，质点之间也没有相对运动。 静止状态包括两种情况： 1、绝对静止：流体整体对地球没有相对运动。
2、相对静止：流体整体对地球有运动，但流体各质点之间没有相对运动。
举例：
绝对静止
等加速水平直线运动 等角速定轴转动
2
第2章 流体静力学
§2.1 流体静压力及其特性
1、静压力的概念
（1）静压力：静止流体作用在单位面积上的压力，称为静压力，或静压强。记作“p”
一点的静压力表示方法：
设静止流体中某一点m，围绕该点取一微小作用面积A，其上压力为P，则： 平均静压力： p P
A
m点的静压力：p lim P
单位：
A0 A
m
国际单位：Pa
物理单位：dyn/cm2
工程单位：kgf/m2
混合单位：1大气压（工程大气压） = 1kgf/cm2
（2）总压力：作用在某一面积上的总静压力，称为总压力。记作“P”
单位：N
3
第2章 流体静力学
2、静压力的两个重要特性
特性一、静压力方向永远沿着作用面内法线方向。

第二章流体静力学

第二章流体静力学
m
图2-1 静止流体中的单元体
pn
τ
2
压力。 压力。 垂向作用力pn指向作用面。
第二章 流体静力学
掌握
二、静压力的两个特性
1．静压力方向永远沿着作用面内法线方向（“内”—指向作用面； ．静压力方向永远沿着作用面内法线方向（ 指向作用面； 指向作用面 法线” 垂直作用面 垂直作用面）。 “法线”—垂直作用面）。 证明：（反证法）如图，取静止流体中任意隔离体。 证明：（反证法）如图，取静止流体中任意隔离体。设切割面上任一 ：（反证法 点 m 处静压力 p 为任意方向。则 p 一定可分解为垂直于作用面的法 为任意方向。 和平行于作用面的切向分力τ。 向分力 pn 和平行于作用面的切向分力 。 p
第二章 流体静力学
A点的压力为 ，则A1、A2点的压力可通过泰勒级数展开得出： 点的压力为p， 点的压力可通过泰勒级数展开得出： 点的压力为
1 ∂p 1 1 ∂2 p 1 2 1 ∂n p 1 n p1 = p(x − dx, y, z) = p(x, y, z) + (− dx) + (− dx) +LL+ (− dx) 2 n 2 ∂x 2 2! ∂ x 2 n! ∂ x 2 1 ∂p 1 1 ∂2 p 1 2 1 ∂n p 1 n p2 = p(x + dx, y, z) = p(x, y, z) + ( dx) + ( dx) +LL+ ( dx) n 2 2 ∂x 2 2! ∂ x 2 n! ∂ x 2
略去二阶以上高阶小量后， 略去二阶以上高阶小量后，得：
z dz 1 ∂p p− dx A1 A 2 ∂x p dy y dx
1 ∂p p1 = p − dx 2 ∂x

第2章静力学

第2章静力学

yD
=
Jc + yc A
yc
！压力中心 D 恒在平面形心 C 的下方。
为什么？
应用上述公式时应该注意： （1）没有考虑大气压的影响。 （2）在压力中心的计算式中y坐标原点的取法。
将y轴原点取在自由液面上。
[例题2-3] 如图所示，一矩形闸门两面受到水的压力，左 边水深H1 = 4.5m，右边水深 H2 = 2.5m ，闸门与水面成 α = 450
四.流体静压力的两个重要特性：
特性一：静压力方向永远沿着作用面内法线方向
p
τ
证明：
pn m
一方面，流体静止时只有法向力，没有切向力，静压力只 能沿法线方向；
另一方面，流体不能承受拉力，只能承受压力。所以，静 压力唯一可能的方向就是内法线方向。
特性二：静止流体中任何一点上各个方向的静压力
大小相等，与作用面方位无关。
说明： 实压力体（+）：压力体内充满液体，垂直分力是向下的； 虚压力体（-）：压力体内没有液体，垂直分力是向上的。 压力体液重并不一定是压力体内实际具有的液体重力，只 是一个虚构概念。
综上所述，压力体的画法可归纳为以下几步：
（1）将受力曲面根据具体情况分成若干段； （2）找出各段的等效自由液面。 （3）画出每一段的压力体并确定虚实。 （4）根据虚实相抵的原则将各段的压力体合成，得到最
受压曲面ab的压力体为V=BAabc。 面积Aabc为扇形面积aob与三角形 cob面积之差，所以有
θ
P
Pz
b
Pz = ρ gBAacb
图2－23 例2－4图
Pz = ρ gBAacb
=
ρgB
⎡α
⎢ ⎣
360
（π H ）2 − sin α

流体力学(张景松版)第二章 流体静力学

流体力学(张景松版)第二章 流体静力学

工程大气压 98066.5 0.98067 1
0.9678 735.6 10.000 735.6 14.22
标准大气压 101325 1.01325 1.033
1
760 10.332 760
14.7
托
133.3 0.00133 0.00136 0.00132 1
13.6
1 0.01934
毫米水柱 9.8067 0.000098 0.0001 0.0000968 0.07356 1 0.07356 0.00142
一、压强的计量
p
1、绝对压强
以完全真空为基准计量的压强
绝对 压强
2、计示（相对）压强
以当地大气压强为基准计量的压强
o
计示 压强
计示 压强 （真空）
p>pa
大气压强 p=pa
p<pa 绝对 压强
完全真空 p=0
表压： p pa pe p pa gh
真空： p pa pv pa p pe
p p dx x 2
o y
dz
b ac
dy dx
p p dx x 2
x
为得到b面和c面的压强，利用a点压强进行泰勒展开:
b(x dx , y, z) : 2
pb

p

p x
dx 2
c(x dx , y, z) : 2
pc

p
p x
dx 2
2 流体静力学
z
p p dx x 2
一、流体的静压强
流体处于绝对静止或相对静止时的压强。
P dP p lim
A0 A dA
2.2 流体的静压力及其特性

第二章流体静力学本章研究流体在静止状态下的力学规律。静止：1

第二章流体静力学本章研究流体在静止状态下的力学规律。静止：1

第二章 流体静力学本章研究流体在静止状态下的力学规律。

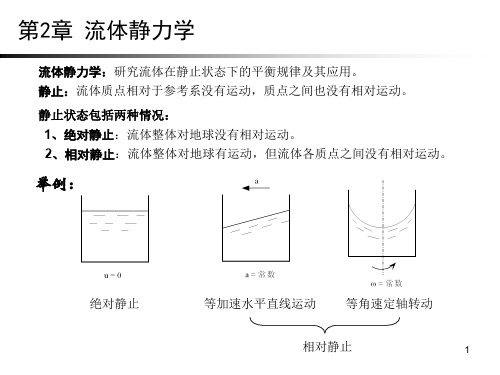
静止：1、流体整体对于地球没有相对运动的叫绝对静止；2、整体相对于地球有相对运动，而流体各质点没有相对运动，称为相对静止。

第1节、作用在流体上的力作用在流体上的力可分为质量力和表面力两类。

一、质量力：作用在流体的每一个质点上，大小与流体M 成正比，对于均质流体与体积V 也成正比。

最常见两类：重力等由于力场引起的惯性力：直线加速运动：达朗伯尔力曲线运动：离心力单位质量的质量力称为单位质量力，常用它来衡量质量力的大小。

设,,x y F F F z 分别表示质量力F v 在x ，y ，z 三轴上的分量，而用X ，Y ，Z 分别表示单位质量力在三坐标轴上的投影，则x x y y z z F F X M V F F Y M V F F Z M V ρρρ⎧==⎪⎪⎪==⎨⎪⎪==⎪⎩设流体只受重力作用，设z 轴铅直向上，则00X Y Mg Z g M⎧⎪=⎪=⎨⎪⎪=−=−⎩ 即单位质量力在数值上就等于加速度，并与加速度量纲相同。

二、表面力：作用在所取流体分离体的表面上的力，并与受作用的流体表面积成比例，单位表面积上的表面力称为应力。

按表面力作用在表面上的方向不同：法向力：与表面法线方向一致切向力：沿表面切线方向作用在上的平均法向应力和平均切向应力分别表示为：SΔ图2-1 作用在流体上的力nn n FP S F SττΔ⎧=⎪⎪Δ⎨Δ⎪=⎪Δ⎩S Δ趋于0（向A 点）并取极限，则可得流体由A 点处的法向应力和切向应力为：lim lim n nS S F dF P S dSF dF S dSτττΔ→∞Δ→∞Δ⎧==⎪⎪Δ⎨Δ⎪==⎪Δ⎩τ是由于流体的粘性和流体具有相对运动而产生的，流体处于静止时，切向应力不再存在，流体表面上就只有法向力，又因流体不能承受拉力，所以法向应力只能指向流体表面的内法线方向，即为流体的静压强。

第二节、流体静压强及其特性流体静压强有两个特性：1、流体静压强的方向垂直于作用面并指向流体内部；2、平衡流体中任意点处的静压强的大小与其作用面的方位无关，只是该点位置坐标的函数，即p=f （x ，y ，z ）。

流体力学第二章流体静力学

流体力学第二章流体静力学
第二章 流体静力学
❖ 流体静力学研究流体的平衡规律，由平衡条 件求静压强分布规律，并求静水总压力。
❖静止是一个相对概念，指流体相对于地球无 运动的绝对平衡和流体相对于地球运动但质点 之间、质点与容器之间无运动的相对平衡。
❖流体质点之间没有相对运动，意味着粘性将 不起作用，所以流体静力学的讨论不须区分流 体是实际流体或理想流体。
pA mhm a
p1左 pA a p1右 mh
2.5.3水银压差计
即使在连通的 静止流体区域中 任何一点的压强 都不知道，也可 利用流体的平衡 规律，知道其中 任何二点的压 差，这就是比压 计的测量原理。
p1左 pA ( z A hm ) p1右 pB mhm zB
面，自由表面上压强为大气压，则液面
以下 h 处的相对压强为 γh ，所以在
液体指定以后,高度也可度量压强，称 为 液 柱 高 ， 例 如 ： ××m(H2O) ， ××mm(Hg) 等。特别地，将水柱高称 为水头。
p=0 h
ph
98 kN/m2=一个工程大气压=10 m(H2O)=736 mm(Hg)
任意形状平面上的静水总压力大 小，等于受压面面积与其形心点 压强的乘积。
2．静水总压力的方向垂直并指 向受压面
3.总压力P的作用点
根据合力矩定理，对x轴
PyD ydP
yy sin dA sin y2dA
p
1 2
p x
dx
dydz
p
1 2
p x
dx
dydz
X
dxdydz
0
化简得：
X 1 p 0
x
Y，z方向可得：
Y Z
1
1
p y p
0

第二章.流体静力学


p0
14
水静力学基本方程：
p p0 gh
结论：重力作用下的均质流体有 1）静水压强随深度按线性规律增加。
A
1 2
A h
h
2）静水压强等于表面压强加上流体的g与该点淹没深度的乘积。
3）自由表面下深度h相等的各点压强均相等——只有重力作用下的 同一连续连通的静止流体的等压面是水平面。(例A—A) 4）推广：已知某点的压强和两点间的深度差，即可求另外一点的 压强值。

三、面积力
1、面积力（Surface Force）：又称表面力，是相邻流体或其它物体 在隔离体表面上的直接施加的接触力。它的大小与作用面面 积成正比。 表面力按作用方向可分为：
5
压力：垂直于作用面。
切力：平行于作用面。
2、应力：单位面积上的表面力，单位： N/m2 或 Pa
压应力 切应力
p lim P A0 A
c.真空（Vacuum）：是指绝对压强小于一个大气压的受压状态。 真空值pv
P
1
pν pa pabs
真空高度
( pabs pa )
0'
p1
p2
pabs1
0' 相对压强基准
2
hv

pv g

pa pabs g
pa
0
pabs2
绝对压强基准 0
注意：计算时无特殊说明时均采用相对压强计算。
pn py F
A
B
px O pz
D
C
x
类似地有：
y
n为斜面ABC的法线方向
质量力：
px p y pz pn
故与作用面的方位无关。
由∑X=0

流体力学(流体静力学)


f (x)
f (x0 )
f (x0 )(!
)
(
x
x0
)
2
f
(n) (x0 n!
)
(x
x0
)n
按泰勒级数展开，把M、N点旳静压强写成
p 1
1 p
pM
p [(x dx) x] x 2
p 2
dx x
p 1
1 p
pN
p
[(x x
dx) x] 2
p
2
dx x
其中 p 为压力在x方向旳变化率。因为微元体旳面积取得足够小，
p1 p2
证明：从静止状态旳流体中引入直角坐标系中二维流体微元来
阐明。
设 y 方向宽度为1。ds 即表达任意方向微元表面。
分析 z 方向旳力平衡
表面力：
p1dscosθ=p1dx和p2dx两个力 二维流体微元旳体积：
z
dV 1 dxdz 2
质量力：
p1ds
ds dz x
θ dx
p3dz
y
Fz
1 2
dp ＝ρ1dU dp ＝ρ2dU 因为ρ1≠ρ2 且都不等于零，所以只有当dp和dU均为零时方程 式才干成立。所以其分界面必为等压面或等势面。
§2－4 流体静力学基本方程
重力作用下压力分布 相对平衡液体旳压力分布
§2—4 流体静力学基本方程
一、重力作用下压强分布
如图所示为一开口容器，其中盛有密度为ρ旳静止旳均匀液体 ，液体所受旳质量力只有重力，又ρ＝常数，重度γ＝ρg也为常数。 单位质量力在各坐标轴上旳分量为
（1）
Z 1 p 0
z
上式称为流体平衡微分方程式，它是 Euler在1755年首先提出 旳，故又称欧拉平衡方程式。它表达流体在质量力和表面力作用下 旳平衡条件。

第二章流体静力学

一、 学习导引1、流体静止的一般方程 （1） 流体静止微分方程x p f x ∂∂=ρ1，y p f y ∂∂=ρ1，zpf z ∂∂=ρ1 （2） 压强微分)(dz f dy f dx f dp z y x ++=ρ（3） 等压面微分方程0=++dz f dy f dx f z y x2、液体的压强分布重力场中，液体的位置水头与压强水头之和等于常数，即C pz =+γ如果液面的压强为0p ，则液面下深度为h 处的压强为h p p γ+=03、 固体壁面受到的静止液体的总压力物体受到的大气压的合力为0。

计算静止液体对物面的总压力时，只需考虑大气压强的作用。

（1） 平面壁总压力：A h P c γ= 压力中心Ay J y y c cc D += 式中，坐标y 从液面起算；下标D 表示合力作用点；C 表示形心。

（2） 曲面壁 总压力：222z y x F F F F ++=分力 ：x xc x A h F γ=，y yc y A h F γ=，V F z γ=4、难点分析（1）连通器内不同液体的压强传递 流体静力学基本方程式的两种表达形式为C pz =+γ和h p p γ+=0。

需要注意的是这两个公式只适用于同一液体，如果连通器里面由若干种液体，则要注意不同液体之间的压强传递关系。

（2）平面壁的压力中心压力中心的坐标可按式Ay J y y c cc D +=计算，面积惯性矩c J 可查表，计算一般较为复杂。

求压力中心的目的是求合力矩，如果用积分法，计算往往还简便些。

（3）复杂曲面的压力体压力体是这样一部分空间体积：即以受压曲面为底，过受压曲面的周界，向相对压强为零的面或其延伸面引铅垂投影线，并以这种投影线在相对压强为零的面或其延伸面上的投影面为顶所围成的空间体积。

压力体内不一定有液体。

正确绘制压力体，可以很方便地算出铅垂方向的总压力。

（4）旋转容器内液体的相对静止液体随容器作等角速度旋转时，压强分布及自由面的方程式为c z g r p +-=)2(22ωγc gr z +=2220ω恰当地选取坐标原点，可以使上述表达式简化。

第二章流体静力学


当四面体的体积趋于零时，可证得px= py=pz=pn
即
p=p(x,y,z)
§2-2 流体的平衡微分方程及积分
一、流体的平衡微分方程
在平衡流体中取如图所示微小正交六面体。分析六面
体在x、y、z方向所受外力，列平衡方程，整理化简得
fx
1
p x
0
fy
1
p y
0
1 p
fz z 0
上式也可用矢量方程表示：
虚压力体：压力体和液体在受压曲面的异侧， Pz向上。
A
A
B
B
例4：试绘制图中abc曲面上的压力体。如已知曲面abc为半圆 柱面，宽度为1m，d=3m，试求abc柱面所受静水压力的水平分 力Px和竖直分力Pz 。
a
d d/2
b 水
水 c
[解] 因abc曲面左右两侧均有水的作用，故应分别考虑。
考虑左侧水的作用
故得欧拉平衡微分方程综合式（即全微分形式）
dp ( f xdx f ydy f z dz)
四.等压面
1.定义： p=C或dp=0的平面或曲面。
2.等压面微分方程
f xdx f y dy f z dz 0
或
f•
ds
0
3.等压面的性质
(1)等压面与等势面重合;
(2)等压面恒与质量力正交。
其作用点为通过体积重心所引出的水平线与受压面的交点D。 当相对压强分布图为三角形时，D点位于自由液面下(2h)/3处。
对于相对压强分布图为梯形情况，可将其分解成三角形和矩 形两部分进行计算后，最后利用合力矩定理求总压力作用点。
例3.铅垂放置的矩形平板闸门，面板后布置三根横梁,各横梁受 力相等,已知闸门上游水头H=4m，试求： （1）每根横梁所受静水总压力的大小； （2）各横梁至水面的距离。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

o x 2 1 h
y h
Z g
∵ ∴
举例：
绝对静止
等加速水平直线运动
等角速定轴转动
1
相对静止
2
第2章 流体静力学
说明：
（1）流体静止时，质点之间没有相对运动，所以流体内不存在切向应 力，作用在流体上表面力只有压力。因此，研究流体在平衡状态下的力 学规律，就是研究流体内的压力分布规律及流体对固体壁面的作用力。 （2）由于粘性力在静止流体中不显示出来，因而本章所论及的力学规 律对理想流体和实际流体都同样适用。
结论： 只有在有势的质量力作用下流体才能保持平衡。
全微分表达式可写为： dp dU 积分，得：p U C C为积分常数。 如果已知液体表面或内部任一点处的U0、p0，则： C p0 U 0 从而， p p0 U U 0 此为在具有力函数U的某一质量力作用下，静止流体内任一点压力p的表达式。 其中，(U－U0)项仅由流体的密度和质量力的势函数所决定，与p0无关。 p0变化，则p相应大小也变化。因而可得到结论： 在平衡状态下的不可压缩流体中，作用在其边界面上的压力，将 等值、均匀地传递到流体的所有各点。
dp
p p p dx dy dz x y z
1、方程的建立
采用微元体分析法 ① 取微单元体 在静止流体中取一微小正交六面体， 各边长分别为 dx、dy、dz，分别与对 应坐标轴平行，六面体中心为A。
10
3、静压力特性的适用范围
（1）适用于流体内部 在进行静压力测定时，根据特性二，只需确定探头的位置即可，不用考虑方向。 （2）适用于流体与固体的交界面 在进行容器器壁的受力分析时，根据特性一，流体静压力垂直于器壁，并指向壁面。
根据泰勒级数展开：
质量力：六面体在 x 方向质量力为：X dxdydz ③ 列力的平衡方程
2 n
1 p1 p x dx, y, z 2 p 1 1 2 p 1 1 n p 1 p x, y, z dx dx dx x 2 2 x 2 2 n! x n 2
m 国际单位：Pa 物理单位：dyn/cm2 工程单位：kgf/m2 混合单位：1大气压（工程大气压） = 1kgf/cm2
P A
（2）总压力：作用在某一面积上的总静压力，称为总压力。记作“P”
3
单位：N
4
第2章 流体静力学
2、静压力的两个重要特性
特性一、静压力方向永远沿着作用面内法线方向。 反证法：假设静压力不沿内法线方向，则只能有以下两种情况： ① 沿任意方向 ② 沿外法线方向 有切向分力 流体受拉力 都将破坏流体平衡。
由于pn的方向是任意取的，所以上式表明：静止流体中同一点处各个方向的 静压力均相等，与作用面方位无关。证毕！ 8
第2章 流体静力学
因此，可以把同一点各个方向的静压力都直接写成 p，只是流体中不同点处的静压 力是不同的，与该点所处的位置有关。在连续介质中，一点的静压力p将是点坐标 的连续函数，即：
第2章 流体静力学
第2章 流体静力学
特性二、静止流体中任何一点上各个方向的静压力大小相等，与作用面方位无关。
证明：采用微元体分析法 ① 取微单元体
在静止流体中，在O点附近取出各边长分别 为dx、dy、dz的微小四面体OABC。相应坐标 轴为x、y、z。
这与静止前提不符，故假设不成立，则原命题成立。
② 受力分析
表面力：只有法向应力，即静压强。微元面积 上的静压强可近似认为是均匀分布的。 以px、py、pz 和 pn分别代表流体作用在OBC、 OAC、 OAB和ABC（n的方向 是任意的）上的平均压强，则各面上的总压力为： ① ②
∵ ∴
dp
p p p dx dy dz x y z
dp Xdx Ydy Zdz
此为流体平衡微分方程式的全微分形式。
14
第2章 流体静力学
对于上式： dp Xdx Ydy Zdz ，如果流体不可压缩， = const，
第2章 流体静力学
15
Xdx Ydy Zdz 也应该是某一函数的全微分上式才有意义。
设此函数为 U x, y, z ，则
又
dU Xdx Ydy Zdz U U U dz dy dx dU z y x
U x U Y y U Z z
China University of Petroleum
第2章 流体静力学
流体静力学：研究流体在静止状态下的平衡规律及其应用。 静止：流体质点相对于参考系没有运动，质点之间也没有相对运动。
第2章 流体静力学
静止状态包括两种情况： 1、绝对静止：流体整体对地球没有相对运动。 2、相对静止：流体整体对地球有运动，但流体各质点之间没有相对运动。
19 20
是




第2章 流体静力学
（3）两种互不相混的平衡流体的交界面是等压面。 设dp为分界面上极近两点的压强差，dU为分界面上极近两点的力势差。 对密度1流体：dp 1dU 1 对密度2流体：dp 2 dU
p1 p2
第2章 流体静力学
§2.3 重力作用下的流体平衡
欧拉平衡方程方程式是一普遍规律，在任何质量力作用下都是适用的。 工程上最常见的情况是质量力只有重力作用下的情况，例如：绝对静止 就属于这种情况。下面对这种平衡情况的压力分布规律进行讨论。
上两式相比较，则得： X
U x, y, z ——力函数（势函数）
具有这样的力函数的质量力称为有势的力，例如：重力、惯性力。
这就是著名的帕斯卡定律（巴斯加定律）。
16
第2章 流体静力学
第2章 流体静力学
3、等压面
等压面：指在同一种、连续的静止流体中，静压力相等的各点所组成的面。
水压机
等压面上，p = const，则：dp 0 由 dp Xdx Ydy Zdz ，得等压面微分方程式：
第2章 流体静力学
§2.1
流体静压力及其特性
1、静压力的概念
（1）静压力：静止流体作用在单位面积上的压力，称为静压力，或静压强。记作“p”
一点的静压力表示方法：
设静止流体中某一点m，围绕该点取一微小作用面积A，其上压力为P，则： 平均静压力： p
P A
A0
m点的静压力：p lim 单位：
1 p X x 0 1 p 0 Y y 1 p 0 Z z
x
第2章 流体静力学
2、方程的积分
1 p X x 0 1 p 0 Y y 1 p 0 Z z
9
第2章 流体静力学
② 受力分析 现以 x 方向为例： 表面力：对平衡流体，表面力只有压力。设中心A点坐标为（x,y, z），其 压力为 p，根据连续性假设，则
第2章 流体静力学
略去二阶以上各项，得：
p1 p 1 p dx 2 x 1 p dx 2 x
同理：
p p ( x, y , z )
Xdx Ydy Zdz 0
F1 F2 A1 A2
帕斯卡（Pascal，Blaise） （1623-1662) ，是法国 著名的数学家、物理学家、 哲学家和散文家 应用：当已知X、Y、Z时，可求出等压面方程，确定等压面形状。
例：当质量力只有重力作用时，如图所示。
X Y 0,
gdz 0
1 p 1 p dx dydz p dx dydz X dxdydz 0 x方向合力为零： p 2 x 2 x
11 12
第2章 流体静力学
合并，得： p dxdydz X dxdydz 0 同除以质量dxdydz，整理得： X 1 p 0 x 1 p 同理可得：Y 0 y 1 p Z 0 z 上述三式称为流体平衡微分方程式（或欧拉平衡方程式）
§2.2 流体平衡微分方程式
为了得到静压力 p p x, y, z 的具体分布表达式，必须首先研究平衡状 态下流体的受力（压力与质量力）应满足的关系，建立流体平衡微分方 程式。然后根据平衡状态下质量力分布，将方程进行积分，便可得到静 压力分布规律。
p p x, y , z
其全微分形式为：
∴ z C 常数 为一簇水平面。
Z g
代入等压面微分方程，得：
千斤顶
17


绝对静止流体
18
即质量力只有重力作用下的静止流体的等压面是水平面。
第2章 流体静力学
下面所取的水平面哪个是等压面？
第2章 流体静力学
等压面的三个特性：
（1）等压面就是等势面。 等压面上，p = const，dp = 0 由dp = dU，得 dU = 0，则U = const 不是 （2）等压面上任一点的质量力必与该等压面相垂直。 在等压面上任取一点，所受单位质量力为： f Xi Yj Zk 在等压面上移动任意微小位移：dl dxi dyj dzk ∴ 质量力做功：f dl Xdx Ydy Zdz 0 ∵ f ， dl 都不为零 ∴ f dl，由此可知：质量力与等压面互相垂直。 应用：① 已知质量力方向，求等压面的形状； ② 已知等压面形状，确定质量力方向。
③ 列力的平衡方程
1 1 x方向： p x dydz pn S ABC cosn, x X dxdydz 0 6 2
∵
S A 2
∴ 上式变为：
1 1 1 p x dydz pn dydz X dxdydz 0 2 2 6 当dx、dy、dz→0时，四面体缩小为O点，上式中的质量力和前二项表面力相