附和导线1计算

第三节 导线测量的内业计算导线测量内业计算的目的就是计算各导线点的平面坐标x 、y 。

计算之前，应先全面检查导线测量外业记录、数据是否齐全，有无记错、算错，成果是否符合精度要求，起算数据是否准确。

然后绘制计算略图，将各项数据注在图上的相应位置，如图6-11所示。

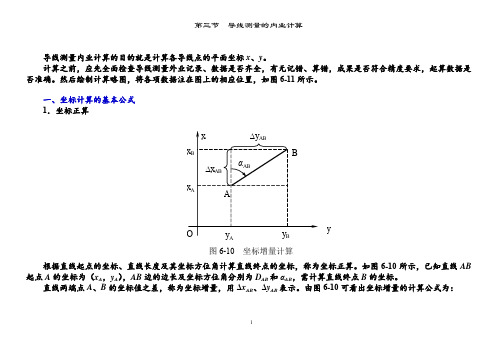
一、坐标计算的基本公式 1．坐标正算根据直线起点的坐标、直线长度及其坐标方位角计算直线终点的坐标，称为坐标正算。

如图6-10所示，已知直线AB 起点A 的坐标为（x A ，y A ），AB 边的边长及坐标方位角分别为D AB 和αAB ，需计算直线终点B 的坐标。

直线两端点A 、B 的坐标值之差，称为坐标增量，用Δx AB 、Δy AB 表示。

由图6-10可看出坐标增量的计算公式为：y图6-10坐标增量计算⎭⎬⎫=-=∆=-=∆AB AB A B AB AB AB A B AB D y y y D x x x ααsin cos （6-1）根据式（6-1）计算坐标增量时，sin 和cos 函数值随着α角所在象限而有正负之分，因此算得的坐标增量同样具有正、负号。

坐标增量正、负号的规律如表6-5所示。

⎭⎬⎫+=∆+=+=∆+=AB AB A AB A B AB AB A AB A B D y y y y D x x x x ααsin cos （6-2）例6-1 已知AB 边的边长及坐标方位角为456380m 62.135'''︒==AB AB D α，，若A 点的坐标为m 82.658m 56.435==A A y x ，，试计算终点B 的坐标。

解 根据式（6-2）得m 62.792456380sin m 62.135m 82.658sin m 68.457456380cos m 62.135m 56.435cos ='''︒⨯+=+=='''︒⨯+=+=AB AB A B AB AB A B D y y D x x αα2．坐标反算根据直线起点和终点的坐标，计算直线的边长和坐标方位角，称为坐标反算。

新光快速路工程第九合同段
（K12+823.608—K15+200）
第
九
标
段
控
制
点
说
明
编制人：审核人：
批准人：
编制单位：
日期：年月日
新光快速路第九标段导线联测说明
为保障现场施工精度的需要，对本标段所有加密导线点进行联测，贯通成一条导线。

其中Q2,Q3边长过短,所以本次贯通测量暂不考虑。

本条导线是附和导线，以J28～J31为起算边，经过Z1，Z2，Q1，Z5，Z6，以GPS35～GPS35为附和边。

整条路线测量完成后计算结果。

计算公式如下：
坐标增量计算公式：△X=Scosα△Y=Ssinα
坐标闭合差计算公式：f X=X′-X f Y=Y′-Y
导线全长闭合差计算公式：f S= f X² +f Y²
坐标改正计算公式：V△Xij= －f X/ΣS×S ij
V△Yij=－f Y/ΣS×S ij
最后坐标增量为：△X ij= △X ij′+ V△Xij
△Y ij=△Y ij′+ V△Yij
此次复测导线线路图为：
复测成果计算结果见下页
附合导线计算表。

一．坐标计算以下为基本计算公式：直线上计算公式：已知该条直线的方位角à，已知直线的起点或终点的坐标，顺线路方向时，计算点的里程知道，直线的起点或终点的里程知道，可推算出计算点与直线的起点的直线距离d，（即计算点的里程减去起点的里程，逆线路方向时，为直线终点的里程减去计算点的里程），计算坐标增量：∆x=d×cosà∆y=d×cosà计算点的坐标为，直线的起点或终点坐标加上坐标增量，式中方位角à从直线起点算时，为已知即给定的方位角，而从终点算时，à为该段直线的起始方位角加上180度。

à+180à起点计算点终点第一种曲线为两段直线中加一圆曲线，指仅存在圆曲线，如下第1点。

1．圆曲线上计算点相对于ZY或YZ 点的弦长和偏角D=2 RSinδδ=90×L/（πR）δ---------圆曲线偏角D ---------弦长L --------为弧长α=α(zy)+δα------------为计算点的方位角,此α为顺着线路方向计算时。

α=α(yz)-δα------------为计算点的方位角,此α为逆着线路方向计算时。

α(zy)、α(yz)---------为圆曲线的起始方位角。

一般为已知。

计算点相对与直圆点或圆直点的坐标增量：△x=D*COSα△y=D*SINα坐标增量计算完毕后，要算某一点的坐标，用直圆点或圆直点的坐标加上计算点与直圆点或圆直点的坐标增量，即为计算点的坐标。

缓和曲线同理。

第二种曲线为两段直线中始端加一缓和曲线，末端加一缓和曲线，两段缓和曲线中加一圆曲线，如下第2点。

2．缓和曲线上计算点相对于HY或YH点的弦长和偏角δ=L²/6RL0X1=L-(L^5/40R²L0²)Y1=L³/6RL0D=√(X1²+Y1²)α=α(hy)+δα------------为计算点的方位角,此α为顺着线路方向计算时。

附合导线平差计算过程说明1）道路观测左角∑β测左=308°2.'38"+70°35'41"+156°56'39"+185°39'2"+205°21'59"+174°36'43"+197°31'46"+157°36'36"+135°14'40"+167°38'50"=1759°14'34"ƒβ测=a始边- a终边=-15"。

ƒβ容=± 40√n =±126"。

ƒβ测＜ƒβ容，测角精度符合要求。

2）改正角：β=β测- ƒβ测/N。

3）坐标方位角的推算：根据起始边的坐标方位角及改正角，依据公式a下一边’= a始边+180°+转角（观测转左角）依次计算各边的坐标方位角。

4）坐标增量的计算及闭合差的调整坐标增量计算根据已经推算出的导线各边的坐标方位角和相应边的边长，按下面公式计算各边的坐标增量。

△ X AB=D AB*COS a AB，△ Y AB=D AB*SIN a AB，按附合导线要求，各边的坐标增量代数和的理论植，等于终起两点的已知坐标之差，所以，纵、横坐标增量闭合差按公式计算，Fx=∑△x测-（X终-X起）FY=∑△Y测-（Y终-Y起）导线全长闭合差f=√(ƒx2+ƒy2)=0.102m,k=f/∑D=1/38370＜1/2000.满足精度要求。

5）根据后一点的坐标及改正后的坐标增量，按公式推算前一点坐标。

X前=X后+△x改Y前=Y后+△Y改最后，推算出终止边的坐标，与原有设计值相等，以作检核。

附合导线计算方法已知A （X=，Y=），B （X=,Y=），C （X=,Y=），D （X=，Y=）四点坐标，及a AB （起始边），a CD （终止边）计算得出。

ƒAB =tan -1(XA XB YA YB --)=tan -1(2507.6983.229963.12158.1303--)=-22。

59”’ =-22。

59”’+180=157000”52’(计算方位角为负，所以要加上180)同理求出ƒCD 方位角坐标为46045”23’1:用求出 ƒAB ±观测角（左正右负）±180，依次加减，得出最后的ƒ‘CD 方位角，用计算的方位角ƒ‘CD -ƒCD =闭合差值B1方位角=157000”52’-192。

14，24，，+180=144。

46，28，，12方位角=144。

46，28，，-236。

48，36，，+180=87。

57，52，，23方位角=87。

57，52，，-170。

39，36，，，+180=97。

38，16，， 34方位角=97。

38，16，，-180。

00，48，，+180=97。

17，28，，4C 方位角=97。

17，28，， -230。

32，36，，+180=46。

44，52，，ƒ‘CD -ƒCD =46。

44，52，，-46045”23’=-31” 将角度闭合差除与测边数分配到各观测角中即：-31÷5=”（角度闭合差调整中，观测角为左角时反符号平均分配到各观测角中,观测角为右角时，则按闭合差同符号分配到测角，如有小数,按长边少分,短边多分原则)即：B1观测角=192。

14，24，，-6”=192。

14，18，，12观测角=236。

48，36，，-6”=236。

48，30，，23观测角=170。

39，36，，-6”=170。

39，30，，34观测角=180。

00，48，，-7”=180。

00，41，，4C 观测角=230。

32，36，，-6”=230。

附合导线测量方法
附合导线测量方法是测量电力系统中电流的一种方法，其原理是在电力系统中添加一个或多个附合导线，使电流经过这些附合导线，再由这些附合导线中的电场感应出电压。

通过测量这些感应出的电压，便可计算出电流的大小。

实际操作中，通常采用两种附合导线测量方法：
1. 单导线法：在电力系统中添加一个附合导线，在该附合导线和被测电流之间加装一个电阻，再通过测量该电阻两端的电压，即可计算出电流的大小。

2. 双导线法：在电力系统中添加两个平行的附合导线，通过测量这两个附合导线之间的电压差，即可计算出电流的大小。

需要注意的是，附合导线测量方法只适用于交流电流的测量，而不能用于直流电流的测量。

测绘中级附合导线测量的内业计算的方法步骤-CAL-FENGHAI.-(YICAI)-Company One1第三节 导线测量的内业计算导线测量内业计算的目的就是计算各导线点的平面坐标x 、y 。

计算之前，应先全面检查导线测量外业记录、数据是否齐全，有无记错、算错，成果是否符合精度要求，起算数据是否准确。

然后绘制计算略图，将各项数据注在图上的相应位置，如图6-11所示。

一、坐标计算的基本公式1．坐标正算根据直线起点的坐标、直线长度及其坐标方位角计算直线终点的坐标，称为坐标正算。

如图6-10所示，已知直线AB 起点A 的坐标为（x A ，y A ），AB 边的边长及坐标方位角分别为D AB 和αAB ，需计算直线终点B 的坐标。

直线两端点A 、B 的坐标值之差，称为坐标增量，用Δx AB 、Δy AB 表示。

由图6-10可看出坐标增量的计算公式为：⎭⎬⎫=-=∆=-=∆AB AB A B AB AB AB A B AB D y y y D x x x ααsin cos （6-1）y图6-10 坐标增量计算根据式（6-1）计算坐标增量时，sin 和cos 函数值随着α角所在象限而有正负之分，因此算得的坐标增量同样具有正、负号。

坐标增量正、负号的规律如表6-5所示。

表6-5 坐标增量正、负号的规律则B 点坐标的计算公式为：⎭⎬⎫+=∆+=+=∆+=AB AB A AB A B AB AB A AB A B D y y y y D x x x x ααsin cos （6-2） 例6-1 已知AB 边的边长及坐标方位角为456380m 62.135'''︒==AB AB D α，，若A 点的坐标为m 82.658m 56.435==A A y x ，，试计算终点B 的坐标。

解 根据式（6-2）得m 62.792456380sin m 62.135m 82.658sin m 68.457456380cos m 62.135m 56.435cos ='''︒⨯+=+=='''︒⨯+=+=AB AB A B AB AB A B D y y D x x αα2．坐标反算根据直线起点和终点的坐标，计算直线的边长和坐标方位角，称为坐标反算。

附合导线严密平差算法总结图1如图的单一附合导线，有4个已知点A、B、C、D，2个未知点TP1、TP2。

设观测边数为n, 则未知点数为n-1, 观测角数为n+1。

以上图为例，n = 3。

观测边为：S1 = B->TP1,S2 = TP1->TP2, S3 = TP2->C思路：由于A、B坐标已知，则可以算出起始方位角，再根据B点坐标和每个观测角（夹角，左角）推算出TP1、TP2、C点的近似坐标值。

如果是用全站仪进行测量，则用盘左盘右重复观测求平均的方式，直接测出TP1、TP2、C点的近似坐标值以及CD的方位角。

再根据c点的已知坐标与近似坐标求坐标闭合差，由CD的已知方位角和近似方位角求角度闭合差，两个闭合差联立求得边长和角度的改正数，最后求得未知点的坐标平差值。

条件平差过程：1.建立条件方程，求得条件系数2.求法方程系数3.求权阵4.计算出联系数K5.解算出观测值改正数V6.由观测值和改正数计算平差值详细步骤如下：1、建立条件方程在单一附合导线中，只需要三个条件方程即：方位角附合条件、纵坐标附合条件和横坐标附合条件方程。

（省略了条件方程的推导过程，详细过程请查看参考资料：《测量平差.pps》）（1）方位角附合条件[Vβi]n+11+ Wβ= 0式中，Wβ= - （T0– T CD+ [βi]n+11 - （n+1）*180°）（角度闭合差）βi ——角度观测值（夹角，左角）Vβi ——各观测角的改正数。

如果是用全站仪观测，则Wβ= - （T CD– T CD）式中，T CD ——CD的方位角观测值，T CD ——CD的已知方位角（2）纵坐标X附合条件方程[Cos TI * VSi]1n - （1/ ρ”）* [(Yn+1- Yi) * Vβi]1n - W x = 0;式中，TI——各方位角观测值（近似值）VSi——边长改正数Yn+1—— C点即终止点的横坐标Y的观测值（近似值）Yi——待定点的横坐标Y的观测值Wx = - （Xn+1- XC）XC—— C点即终止点的纵坐标X的已知值ρ” = 2062.65（3）横坐标Y附合条件方程[Sin TI * VSi]1n + （1/ ρ”）* [(Xn+1- Xi) * Vβi]1n– W Y = 0;式中，TI——各方位角观测值（近似值）VSi——边长改正数Xn+1—— C点即终止点的纵坐标X的观测值（近似值）Xi——待定点的纵坐标X的观测值WX = - （Yn+1- YC）YC—— C点即终止点的横坐标Y的已知值ρ” = 2062.652、求条件方程的系数矩阵联立3个方程得改正数条件方程组：[Vβi]n+11+ Wβ= 0[Cos TI * VSi]1n - 1/ ρ”* [(Yn+1- Yi) * Vβi]1n - W x = 0;[Sin TI * VSi]1n + 1/ ρ”* [(Xn+1- Xi) * Vβi]1n– W Y = 0;其系数矩阵arrA为：（即改正数V的系数，此处以图1为例， n = 3）3、联系数法方程（简称法方程）AP-1A T K – W = 0A——系数矩阵arrAK ——乘系数P ——权阵W ——闭合差矩阵由上得法方程的系数阵N：N = AP-1A T（权的推导见参考资料：《全站仪观测导线测量平差方法的研究.pdf》）角度权：P βi = 1；（因为角度的标称精度是固定的，各观测角权值相等） 边长权：P Si = (μ0 *μ0 ) / （M D * M D ）（误差比例系数固定，边长的误差与距离有关，因此不一致）式中，μ0 ——先验测角中误差，以秒为单位 M D —— 距离观测中误差若 导线边长为S i （米），e1 为仪器的边长标称固定误差（mm ），e2为仪器的边长比例误差系数（无单位），则M D = ± （e1 + e2 * S i * 0.001）mm 需转化为厘米：M D = M D ** 0.1 （cm ）由于此处是要P 的逆矩阵P -1,因此要求P 的各元素的倒数（P 是对角矩阵，对角矩阵的逆矩阵就是原矩阵元素的倒数） Psi = 1/ Psi ；由上可得，P -1 矩阵如下：4、求改正数由于N 已经在前面的步骤中求出，求N 的逆矩阵。

附合导线测量的内业计算第三节导线测量的内业计算导线测量内业计算的⽬的就是计算各导线点的平⾯坐标x 、y 。

计算之前，应先全⾯检查导线测量外业记录、数据是否齐全，有⽆记错、算错，成果是否符合精度要求，起算数据是否准确。

然后绘制计算略图，将各项数据注在图上的相应位置，如图6-11所⽰。

⼀、坐标计算的基本公式 1．坐标正算根据直线起点的坐标、直线长度及其坐标⽅位⾓计算直线终点的坐标，称为坐标正算。

如图6-10所⽰，已知直线AB 起点A 的坐标为（x A ，y A ），AB 边的边长及坐标⽅位⾓分别为D AB 和αAB ，需计算直线终点B 的坐标。

直线两端点A 、B 的坐标值之差，称为坐标增量，⽤Δx AB 、Δy AB 表⽰。

由图6-10可看出坐标增量的计算公式为：=-=?=-=?AB AB A B AB AB AB A B AB D y y y D x x x ααsin cos （6-1）根据式（6-1）计算坐标增量时，sin 和cos 函数值随着α⾓所在象限⽽有正负之分，因此算得的坐标增量同样具有正、负号。

坐标增量y图6-10坐标增量计算正、负号的规律如表6-5所⽰。

+=?+=+=?+=AB AB A AB A BAB AB A AB A B D y y y y D x x x x ααsin cos （6-2）例6-1 已知AB 边的边长及坐标⽅位⾓为456380m 62.135'''?==AB AB D α，，若A 点的坐标为m 82.658m 56.435==A A y x ，，试计算终点B 的坐标。

解根据式（6-2）得m 62.792456380sin m 62.135m 82.658sin m68.457456380cos m 62.135m 56.435cos ='''??+=+=='''??+=+=AB AB A B AB AB A B D y y D x x αα2．坐标反算根据直线起点和终点的坐标，计算直线的边长和坐标⽅位⾓，称为坐标反算。