最短路径分析

八年级最短路径问题归纳最短路径问题是图论中的一个经典问题，也是计算机科学中的重要研究领域之一。

在八年级的学习中，我们也会接触到最短路径问题，并且通过一些简单的算法来解决这个问题。

本文将对八年级最短路径问题进行归纳总结，希望能够帮助大家更好地理解和应用这个问题。

一、最短路径问题的定义最短路径问题是指在一个给定的图中，找出两个顶点之间的最短路径，即路径上的边权之和最小。

其中，图由顶点和边组成，顶点表示路径中的点，边表示路径中的通路或连接。

二、最短路径问题的应用最短路径问题在生活中有着广泛的应用，比如导航系统中的最短路径规划、货物运输中的最短路径选择等等。

通过寻找最短路径，可以帮助我们节省时间和资源，提高效率。

三、最短路径问题的解决方法1. 迪杰斯特拉算法迪杰斯特拉算法是解决最短路径问题的一种常用算法。

该算法通过不断更新起点到各个顶点的最短路径，直到找到终点的最短路径为止。

迪杰斯特拉算法的具体步骤如下：- 初始化起点到各个顶点的距离为无穷大，起点到自身的距离为0；- 选择一个未访问的顶点，更新起点到其他顶点的距离；- 重复上述步骤，直到找到终点的最短路径或所有顶点都被访问过。

2. 弗洛伊德算法弗洛伊德算法是解决最短路径问题的另一种常用算法。

该算法通过不断更新任意两个顶点之间的最短路径，直到更新完所有顶点对之间的最短路径为止。

弗洛伊德算法的具体步骤如下：- 初始化任意两个顶点之间的距离，如果两个顶点之间有直接的边，则距离为边的权值，否则距离为无穷大；- 选择一个顶点作为中转点，更新任意两个顶点之间的距离；- 重复上述步骤，直到更新完所有顶点对之间的最短路径。

四、最短路径问题的注意事项在解决最短路径问题时，需要注意以下几点：1. 图的表示方式：可以使用邻接矩阵或邻接表来表示图，根据具体的问题选择合适的表示方式。

2. 边的权值：边的权值可以表示两个顶点之间的距离、时间、花费等等，根据具体的问题选择合适的权值。

将军行军——最短路径问题的解析方法1. 引言最短路径问题是在图论中广泛研究的一个问题，它涉及在给定的图中寻找两个节点之间的最短路径。

在将军行军中，解决最短路径问题对于制定有效的行军策略至关重要。

本文将介绍一种解析最短路径问题的方法。

2. 解析方法解析最短路径问题的方法包括以下步骤：2.1 创建图首先，我们需要根据行军地图创建一个图。

图由节点和边组成，节点代表行军地点，边代表行军路径。

节点之间的距离可以表示为边的权重。

2.2 确定起点和终点在解析最短路径问题之前，需要明确起点和终点。

起点是将军的当前位置，终点是将军需要到达的目的地。

2.3 应用最短路径算法选择适用的最短路径算法，如Dijkstra算法或A*算法。

这些算法可以根据节点之间的距离和权重来计算最短路径。

2.4 寻找最短路径应用最短路径算法后，可以得到从起点到终点的最短路径。

这条路径由一系列节点和边组成，表示将军行军的最佳路径。

3. 实例应用以下是一个将军行军的实例应用：3.1 创建图假设将军需要从A地到达B地，行军地图如下所示：A---5---B/ \3 2\ /C---4---D在这个图中，节点A、B、C和D代表不同的行军地点，边的权重表示行军路径的距离。

3.2 确定起点和终点假设起点为节点A，终点为节点B。

3.3 应用最短路径算法选择Dijkstra算法来解决最短路径问题。

3.4 寻找最短路径应用Dijkstra算法后，得到从节点A到节点B的最短路径为A->C->D->B，总距离为9。

4. 结论通过解析最短路径问题，我们可以为将军行军制定最佳的路径策略。

通过创建图、确定起点和终点、应用最短路径算法和寻找最短路径，我们可以找到将军行军的最短路径，并确保行军效率。

这种解析方法可以在实际的将军行军中得到应用，提高行军的效率和战术优势。

以上是最短路径问题的解析方法及其实例应用。

希望对将军行军策略的制定有所帮助。

参考文献- 张三, 李四. 图论及其应用. XX出版社, 20XX.。

初中最短路径问题7种类型初中最短路径问题7种类型最短路径问题是离散数学中一个重要的研究领域，其应用广泛，包括交通路线规划、网络优化等。

对于初中学生来说，了解和掌握最短路径问题，有助于培养他们的逻辑思维和解决问题的能力。

下面将介绍初中最短路径问题的七种类型。

1. 单源最短路径问题单源最短路径问题是指在一个给定的加权有向图中，从一个确定的源点出发，求到其他所有顶点的最短路径。

这个问题可以通过使用迪杰斯特拉算法或贝尔曼-福特算法来求解。

通过学习和理解这些算法，学生可以逐步掌握寻找最短路径的基本方法。

2. 多源最短路径问题多源最短路径问题是指在一个给定的加权有向图中，求任意两个顶点之间的最短路径。

这个问题可以通过使用佛洛依德算法来解决。

学生可以通过了解和实践佛洛依德算法，掌握多源最短路径问题的求解方法。

3. 无权图最短路径问题无权图最短路径问题是指在一个无向无权图中，求从一个顶点到其他所有顶点的最短路径。

这个问题可以通过使用广度优先搜索算法来解决。

学生可以通过学习广度优先搜索算法，了解和掌握无权图最短路径问题的解决方法。

4. 具有负权边的最短路径问题具有负权边的最短路径问题是指在一个给定的加权有向图中，存在负权边，求从一个顶点到其他所有顶点的最短路径。

这个问题可以通过使用贝尔曼-福特算法来解决。

学生可以通过了解和实践贝尔曼-福特算法，理解和应用具有负权边的最短路径问题。

5. 具有负权环的最短路径问题具有负权环的最短路径问题是指在一个给定的加权有向图中，存在负权环，求从一个顶点到其他所有顶点的最短路径。

这个问题可以通过使用贝尔曼-福特算法的改进版来解决。

学生可以通过学习和理解贝尔曼-福特算法的改进版，解决具有负权环的最短路径问题。

6. 具有边权和顶点权的最短路径问题具有边权和顶点权的最短路径问题是指在一个给定的加权有向图中，除了边权之外，还考虑了顶点的权重，求从一个顶点到其他所有顶点的最短路径。

这个问题可以通过使用约翰逊算法来解决。

《最短路径问题》教学设计一、教学目标（一）知识与技能：能利用轴对称等图形变换，依据“两点之间，线段最短”或“三角形两边之和大于第三边”解决最短路径问题．（二）过程与方法：在观察、操作、想象、论证、交流的过程中，获得解决最短路径问题的基本思路及经验．（三）情感态度与价值观：体会图形的变化在解决最值问题中的作用，感悟转化思想，在实际问题中迁移使用所获得的基本经验，深入领会其应用价值．二、教学重点和难点（一）教学重点：用轴对称变换以及平移解决实际问题中的最短路径问题．（二）教学难点：学生发现确定最短路径的“路径向导点”.三、教学方法和策略采用“实验—猜测—验证—应用”的教学线索，以学生的知识建构和认识发现为主轴，把线索发现的主动权和问题解决的个性化还给学生．充分利用网络多媒体教学环境和几何画板，制作学生可以动手操作体验的多媒体课件，把抽象的数学理论形象化，学生利用课件创建的图形去发现规律，验证思路，得出结论．让数学学习过程可视化、可操作化并增加互动性．四、教学过程题.二、观看视频，激发兴趣用教师机向学生机广播视频.视频内容1：虫洞(Wormhole)，又称爱因斯坦-罗森桥.视频内容2：朝诗人李颀的诗《古从军行》开头两句说：“白日登山望烽火，黄昏饮马傍交河．”诗中隐含着一个有趣的数学问题．三、分发课件，自主探究【课件引入】“最短路径的选择-看图思考”预设问题：问题：在不同的情景中，怎么合理选择路径呢？【发现】折线路径或立体路径 两点之间，线段最短.【活动1】“读历史故事，智闯六关之第一关”官渡之战，是东汉末年“三大战役”之一，也是中国历史上著名的以弱胜强的战役之一.建安五年（200年），曹操军与袁绍军相持于官渡(今河南中牟东北),在此展开战略决战.曹操奇袭袁军在乌巢的粮仓(今河南封丘西),继而击溃袁军主力.此战奠定了曹操统一中国北方的基础. 在自己的计算机上观看视频.【课件引入】在四幅图片的引领下，学生逐渐发现平面内两点之间的最短路径到立体图形中的最短路径隐含的内在联系.【活动1】学生独立操作：拖动点P，确定点P的位置．意图：引发学生的学习兴趣和思考.融合点：将网络素材与所要学习内容整合，古诗词作为最短路径问题的载体.意图：【课件引入】通过对逐渐递进的四幅图形的思索，培养学生能够用数学的眼光认识生活中现象的能力；将复杂的折线路径或立体路径转化为“两点之间，线段最短”，让学生体验“转化思想”的作用．融合点：取自现实生活中的情景与合理选择路径整合起来，直观形象与抽象思索整合起来.意图：【活动1】通过设置历史背景，将六个问题有机的串联起来，增强趣味本节课以此为背景，设置六关，鼓励学生一一破解. 第一关：曹军先遣队要趁夜色到河对岸的敌军营地营地附近做好埋伏，应该怎样走线路最短？预设问题：先遣队从A，到河对岸敌军营地B，在河流a上求一点P，使得P A+PB最小.预案：如果有的学生不会操作拖动一个点，则及时向学生讲解一下如何拖动点P.【活动2】“智闯六关之第二关”攻占营地后，我军分设马场和营地两个驻扎点，为了给战士和马匹提供饮水，我军计划在河边修建水站，用水渠引水，为了减小挖水渠的工作量，水站应选在何处？预设问题：如图，要在河边修建一个水站，分别向马场A、营地B送水，水站修在河边什么地方可使所挖的水渠最短?预案：如有必要，须向学生讲一下按钮的先后顺序.【活动3】“智闯六关之第三关”为巩固战果，我军修建了两条防御工事，交成一个角，并在它的内部建了弹药库，为了提高运送效率，准备修两【活动2】学生动手操作，在感受图形变化的同时，可以借助表格，定量分析当点C运动过程中AC+BC的值由小到大或由大到小的变化过程，当点C到合适的位置时，AC+BC的值最小.【活动3】学生可以用鼠性，调动学生探究的积极性，在本环节，只是简单拖动一个点，“两点位于一条直线异侧”，很容易将所要确定的点与“两点之间，线段最短”确立联系，本活动每位学生均可无困难的完成．融合点：历史故事+直观图形+抽象的“两点一线”模型结合起来.意图：【活动2】通过使用表格工具，让学生体会定量分析的作用，借助几何画板的动态演示功能，学生可以方便的找到点C，培养学生由数到形的数学思想以及转化的能力．在实验探究的过程中验证所学知识，发展学生的空间想象力.融合点：直观的辅助图形+准确的表格测量数据和空间想象结合.意图：【活动3】条通道从弹药库分别通往工事，应如何设计？预设问题：如图，A是锐角∠MON内部任意一点，在∠MON的两边OM，ON上各取一点D、E，使△ADE周长最小.【活动4】“智闯六关之第四关”侦察兵申请在防御工事内各修建一个瞭望塔，并规划好士兵侦查路线，即从兵营出发，先去往1号瞭望塔，再去2号瞭望塔侦察，侦查完毕去将军营汇报侦察结果.要怎样设计两个瞭望塔的位置，才能使士兵走的路最短？预设问题：在∠MON内有两点A、B，现在从点A先到射线OM 上点C，再到射线ON上点D，最后到达点B，请问最短距离如何确定？【活动5】“智闯六关之第五关”由于敌军近日反抗较强烈，我军需做好撤退计划，为了使战士快速全部撤回原河内营地，需在河上修建桥梁，桥梁应如何选址，才能使战士走的路程最短？标选中D、E中的一个点拖动或两个点同时拖动，感受图形变化引发的数量变化，如果借助表格无法正确确定D、E的位置，则需按“显示辅助线段”和“显示四边形”按钮，当两个四边形都消失的时候，点D、E运动到合适的位置，AD+EA+DE的值最小.【活动4】学生在上一个活动中得到的经验若还不能帮助他们正确找到“两个定点和两个动点在两条射线上运动”这一模型下的点D、E运动到的位置，则发挥小组合作的作用，再由老师引导启发，从而得出AC+CD+DB的值最小.【活动5】通过使用辅助的“显示/隐藏四边形”按钮，让学生体会四点共线时，线段最短.学生如果之前没有学过本题内容，确定点D、E的位置不会很轻松，需要胆大心细，仔细操作、观察、总结方可找到正确的位置.融合点：将一个点作两次关于直线的轴对称和两点之间线段最短结合起来.意图：【活动4】在这一过程中让学生进一步体会作法的合理性，提高了学生的逻辑思维能力.老师的引导，小组的合作，再次体现了老师的主导性，学生的主体性.融合点：将复杂背景中的问题与抽象的两个点作两次关于直线的轴对称结合起来.将直觉猜想和验证结合起来.培养学生严谨的思考习惯.意图：【活动5】“造桥选址”问预设问题：如图，A、B两地在一条河的两岸，现要在河上建一座桥MN，桥造在何处才能使从A到B的路径AMNB最短？（假设河的两岸是平行的直线，桥与河岸垂直）【阶段小结】以上五种情景均为平面内利用轴对称或平移变换将最短路径问题转化为“两点之间，线段最短”.【活动6】“智闯六关之第六关”为了防止敌人返攻，我军战士乔装后去了敌人后方侦察，发现敌军营内有一底面周长为16m，高5m的圆柱形的弹药库，顶部有个通风孔可以进人，在内壁远离我军方向距顶部1m处有一个凹陷，可用来安放炸药，战士手中有10.5m的引线，该战士想安放炸药后，将引线引至弹药库外靠近我方的地面上，点燃后迅速跑离，请问能否实现？说明：先观察下图中，撤退点、烛龛分别对应哪个点？思考最短路径是一条什么类型的线？然后按顺序①[圆柱侧面展开]，②[显示矩形]，③[向上翻折]，思考问题的答案.四、归纳总结，反思提升同学们总结一下，通过本节课借助几何画板所研究的内容，学生可以用鼠标选中点C拖动，感受CD长度不随其位置的改变而变化，也可借助表格确定C、D的位置.【活动6】学生通过思考将一个实际问题转化为一个数学问题，将一个空间问题转化为平面问题，将一个平面问题转化为解三角形，通过操作3D模型将圆柱侧面展开，从而形象直观得到答案.【归纳总结】题有着非常好的实际背景，情境贴近生活．从求解方法看，平移是问题实现转化中的一个重要策略，联想到平移,其本质还是对“两点之间，线段最短”公理的深刻理解．同学们值得认真体会和积累．融合点：将平移作图和求最短路径结合起来.意图：【活动6】通过将圆柱侧面展平，把较复杂的最短路径问题转化为“两点之间，线段最短”问题.融合点：将曲面中的最短路径问题和平面问题的转化结合起来.有何收获和思考？五、巩固练习，适当拓展如图所示，正方形ABCD的面积为12，△ABE是等边三角形，点E在正方形ABCD内，在对角线AC上有一点P，使PD+PE的和最小，求这个最小值.六、一试身手，分层检测专题：最短路径问题小测试A卷学生回顾前面的探究过程，小结解决问题的步骤是怎样的？借助了什么知识解决问题的？体现了什么数学思想？打开链接“专题：最短路径小测试A卷”完成基础题.意图：【归纳总结】让学生养成反思的好习惯，积累解决问题的方法，再次体会转化的数学思想.意图：通过“问卷星”分层检测，实时打分，可以及时反馈学生的掌握程度.融合点：将网络教学环境与满足不同学生发展的需求整合起来.意图：基础题是最短路径问题的简单应用，帮助学生巩固基础.A DEPB C专题：最短路径问题小测试B卷1.在平面直角坐标系中，有A（3，－2），B（4，2）两点，现另取一点C（1，n），当n=时，AC+BC的值最小．打开链接“专题：最短路径小测试B卷”完成提高题. 意图：提高题是“最短路径问题”的升华，考查学有余力的同学掌握情况，并且在课件中有B卷配图，可以帮助有困难的学生借助动态图形降低难度.七、布置作业（基础必做题）做完课上没有完成的：专题：最短路径问题小测试B卷（提高选做题）1.搜集最短路径问题的其他经典题目，并整理在笔记本上.2.阅读“平面几何中的费马问题和费马点”，并与同学们交流. 学生课后完成作业，其中的提高选作题可预留一周时间完成. 意图：为了有效地对学生的学习情况进行反馈，尊重学生的个体差异，满足学生多样化的学习需要，我对作业进行分层布置，分为基础必做题和提高选作题.融合点：搜集其他经典题目的过程和学生用数学整合起来，让学生掌握的能力可以解决最短路径问题.费马点问题和本节课没讲到的旋转变换整合起来，训练了学生寻找问题结论的发散思维.学情分析（一）教学对象分析：最短路径问题从本质上说是最值问题，初二的学生对这类问题比较陌生，经验不足，特别是对于具有实际背景的最值问题，更会无从下手，应让学生牢记两点之间线段最短，从而想到把其中一个点转移到另一侧进行解题．（二）教学环境分析：根据学生理性归纳能力不强的特点，采用几何画板制作成易于学生观察和动手操作的课件，辅助学生验证和增强解决问题的兴趣．运用计算机网络环境授课，方便学生展示、交流和纠错．效果分析本节课的活动设计与评测练习借助多媒体教学环境，有利于教学目标的实现，突出了重点，突破了难点.1.几何画板的软件环境，有利于揭示隐含条件.数学最值问题设计运动、轨迹、存在、最值、任意、不等式等较为抽象复杂的概念，传统方法常常让学生感到力不从心，借助几何画板，使多元抽象关系动态化、直观化，可以促使学生深入理解题意.2.最值求解的过程常常需要建立函数模型，寻求合适的自变量建立函数模型是解题难点．几何画板通过坐标系数形结合、动态直观展示自变量与函数值的内在联系，可有效突破难点．能够抽象出“最短路径问题”数学模型，在探索最短路径的过程中，体会轴对称的“桥梁”作用，感悟转化思想.3、一般而言，解决最值的思维过程比较隐匿．传统教学较难凸显其思维过程．几何画板不仅能动态展示数学关系的多元联系，而且可以视觉化思维过程．《最短路径问题》教学设计一、教学目标（一）知识与技能：能利用轴对称等图形变换，依据“两点之间，线段最短”或“三角形两边之和大于第三边”解决最短路径问题．（二）过程与方法：在观察、操作、想象、论证、交流的过程中，获得解决最短路径问题的基本思路及经验．（三）情感态度与价值观：体会图形的变化在解决最值问题中的作用，感悟转化思想，在实际问题中迁移使用所获得的基本经验，深入领会其应用价值．二、教学重点和难点（一）教学重点：用轴对称变换以及平移解决实际问题中的最短路径问题．（二）教学难点：学生发现确定最短路径的“路径向导点”.三、教学方法和策略采用“实验—猜测—验证—应用”的教学线索，以学生的知识建构和认识发现为主轴，把线索发现的主动权和问题解决的个性化还给学生．充分利用网络多媒体教学环境和几何画板，制作学生可以动手操作体验的多媒体课件，把抽象的数学理论形象化，学生利用课件创建的图形去发现规律，验证思路，得出结论．让数学学习过程可视化、可操作化并增加互动性．四、教学过程视频内容1：虫洞(Wormhole)，又称爱因斯坦-罗森桥.视频内容2：朝诗人李颀的诗《古从军行》开头两句说：“白日登山望烽火，黄昏饮马傍交河．”诗中隐含着一个有趣的数学问题．三、分发课件，自主探究【课件引入】“最短路径的选择-看图思考”预设问题：问题：在不同的情景中，怎么合理选择路径呢？【发现】折线路径或立体路径 两点之间，线段最短.【活动1】“读历史故事，智闯六关之第一关”官渡之战，是东汉末年“三大战役”之一，也是中国历史上著名的以弱胜强的战役之一.建安五年（200年），曹操军与袁绍军相持于官渡(今河南中牟东北),在此展开战略决战.曹操奇袭袁军在乌巢的粮仓(今河南封丘西),继而击溃袁军主力.此战奠定了曹操统一中国北方的基础.本节课以此为背景，设置六关，鼓励学生一一破解. 第一关：曹军先遣队要趁夜色到河对岸的敌军营地营地附近做好埋伏，应该怎样走线路最短？机上观看视频.【课件引入】在四幅图片的引领下，学生逐渐发现平面内两点之间的最短路径到立体图形中的最短路径隐含的内在联系.【活动1】学生独立操作：拖动点P，确定点P的位置．的学习兴趣和思考.融合点：将网络素材与所要学习内容整合，古诗词作为最短路径问题的载体.意图：【课件引入】通过对逐渐递进的四幅图形的思索，培养学生能够用数学的眼光认识生活中现象的能力；将复杂的折线路径或立体路径转化为“两点之间，线段最短”，让学生体验“转化思想”的作用．融合点：取自现实生活中的情景与合理选择路径整合起来，直观形象与抽象思索整合起来.意图：【活动1】通过设置历史背景，将六个问题有机的串联起来，增强趣味性，调动学生探究的积极性，在本环节，只是简单拖动一个点，预设问题：先遣队从A，到河对岸敌军营地B，在河流a上求一点P，使得P A+PB最小.预案：如果有的学生不会操作拖动一个点，则及时向学生讲解一下如何拖动点P.【活动2】“智闯六关之第二关”攻占营地后，我军分设马场和营地两个驻扎点，为了给战士和马匹提供饮水，我军计划在河边修建水站，用水渠引水，为了减小挖水渠的工作量，水站应选在何处？预设问题：如图，要在河边修建一个水站，分别向马场A、营地B送水，水站修在河边什么地方可使所挖的水渠最短?预案：如有必要，须向学生讲一下按钮的先后顺序.【活动3】“智闯六关之第三关”为巩固战果，我军修建了两条防御工事，交成一个角，并在它的内部建了弹药库，为了提高运送效率，准备修两条通道从弹药库分别通往工事，应如何设计？【活动2】学生动手操作，在感受图形变化的同时，可以借助表格，定量分析当点C运动过程中AC+BC的值由小到大或由大到小的变化过程，当点C到合适的位置时，AC+BC的值最小.【活动3】学生可以用鼠标选中D、E中的一个点拖动或两个点同时拖动，感受图形“两点位于一条直线异侧”，很容易将所要确定的点与“两点之间，线段最短”确立联系，本活动每位学生均可无困难的完成．融合点：历史故事+直观图形+抽象的“两点一线”模型结合起来.意图：【活动2】通过使用表格工具，让学生体会定量分析的作用，借助几何画板的动态演示功能，学生可以方便的找到点C，培养学生由数到形的数学思想以及转化的能力．在实验探究的过程中验证所学知识，发展学生的空间想象力.融合点：直观的辅助图形+准确的表格测量数据和空间想象结合.意图：【活动3】通过使用辅助的“显示/隐藏四边形”按钮，让学生体会四预设问题：如图，A是锐角∠MON内部任意一点，在∠MON的两边OM，ON上各取一点D、E，使△ADE周长最小.【活动4】“智闯六关之第四关”侦察兵申请在防御工事内各修建一个瞭望塔，并规划好士兵侦查路线，即从兵营出发，先去往1号瞭望塔，再去2号瞭望塔侦察，侦查完毕去将军营汇报侦察结果.要怎样设计两个瞭望塔的位置，才能使士兵走的路最短？预设问题：在∠MON内有两点A、B，现在从点A先到射线OM 上点C，再到射线ON上点D，最后到达点B，请问最短距离如何确定？【活动5】“智闯六关之第五关”由于敌军近日反抗较强烈，我军需做好撤退计划，为了使战士快速全部撤回原河内营地，需在河上修建桥梁，桥梁应如何选址，才能使战士走的路程最短？变化引发的数量变化，如果借助表格无法正确确定D、E的位置，则需按“显示辅助线段”和“显示四边形”按钮，当两个四边形都消失的时候，点D、E运动到合适的位置，AD+EA+DE的值最小.【活动4】学生在上一个活动中得到的经验若还不能帮助他们正确找到“两个定点和两个动点在两条射线上运动”这一模型下的点D、E运动到的位置，则发挥小组合作的作用，再由老师引导启发，从而得出AC+CD+DB的值最小.【活动5】学生可以用鼠标选中点C拖动，感受CD长度不随其位置点共线时，线段最短.学生如果之前没有学过本题内容，确定点D、E的位置不会很轻松，需要胆大心细，仔细操作、观察、总结方可找到正确的位置.融合点：将一个点作两次关于直线的轴对称和两点之间线段最短结合起来.意图：【活动4】在这一过程中让学生进一步体会作法的合理性，提高了学生的逻辑思维能力.老师的引导，小组的合作，再次体现了老师的主导性，学生的主体性.融合点：将复杂背景中的问题与抽象的两个点作两次关于直线的轴对称结合起来.将直觉猜想和验证结合起来.培养学生严谨的思考习惯.意图：【活动5】“造桥选址”问题有着非常好的实际背景，情境贴近生活．从求解方法看，平预设问题：如图，A、B两地在一条河的两岸，现要在河上建一座桥MN，桥造在何处才能使从A到B的路径AMNB最短？（假设河的两岸是平行的直线，桥与河岸垂直）【阶段小结】以上五种情景均为平面内利用轴对称或平移变换将最短路径问题转化为“两点之间，线段最短”.【活动6】“智闯六关之第六关”为了防止敌人返攻，我军战士乔装后去了敌人后方侦察，发现敌军营内有一底面周长为16m，高5m的圆柱形的弹药库，顶部有个通风孔可以进人，在内壁远离我军方向距顶部1m处有一个凹陷，可用来安放炸药，战士手中有10.5m的引线，该战士想安放炸药后，将引线引至弹药库外靠近我方的地面上，点燃后迅速跑离，请问能否实现？说明：先观察下图中，撤退点、烛龛分别对应哪个点？思考最短路径是一条什么类型的线？然后按顺序①[圆柱侧面展开]，②[显示矩形]，③[向上翻折]，思考问题的答案.六、归纳总结，反思提升同学们总结一下，通过本节课借助几何画板所研究的内容，的改变而变化，也可借助表格确定C、D的位置.【活动6】学生通过思考将一个实际问题转化为一个数学问题，将一个空间问题转化为平面问题，将一个平面问题转化为解三角形，通过操作3D模型将圆柱侧面展开，从而形象直观得到答案.【归纳总结】学生回顾前面的探究过程，小结解决问题的移是问题实现转化中的一个重要策略，联想到平移,其本质还是对“两点之间，线段最短”公理的深刻理解．同学们值得认真体会和积累．融合点：将平移作图和求最短路径结合起来.意图：【活动6】通过将圆柱侧面展平，把较复杂的最短路径问题转化为“两点之间，线段最短”问题.融合点：将曲面中的最短路径问题和平面问题的转化结合起来.意图：【归纳总结】让学生养成反思的好习惯，积有何收获和思考？七、巩固练习，适当拓展如图所示，正方形ABCD的面积为12，△ABE是等边三角形，点E在正方形ABCD内，在对角线AC上有一点P，使PD+PE的和最小，求这个最小值.六、一试身手，分层检测专题：最短路径问题小测试A卷步骤是怎样的？借助了什么知识解决问题的？体现了什么数学思想？打开链接“专题：最短路径小测试A卷”完成基础题.累解决问题的方法，再次体会转化的数学思想.意图：通过“问卷星”分层检测，实时打分，可以及时反馈学生的掌握程度.融合点：将网络教学环境与满足不同学生发展的需求整合起来.意图：基础题是最短路径问题的简单应用，帮助学生巩固基础.A DEPB C专题：最短路径问题小测试B卷1.在平面直角坐标系中，有A（3，－2），B（4，2）两点，现另取一点C（1，n），当n=时，AC+BC的值最小．打开链接“专题：最短路径小测试B卷”完成提高题.意图：提高题是“最短路径问题”的升华，考查学有余力的同学掌握情况，并且在课件中有B卷配图，可以帮助有困难的学生借助动态图形降低难度.。

最短路径问题及其变形最短路径问题及其变形【摘要】本文将详细介绍最短路径问题及其变形。

最短路径问题是图论中的经典问题之一，通过求解最短路径，我们可以在许多实际应用中找到最优的路径选择方案。

本文将从最短路径问题的基本定义出发，逐渐深入探讨最短路径问题的相关概念和算法，并介绍常见的最短路径问题的变形和应用场景。

通过学习本文，读者将对最短路径问题有全面、深刻和灵活的理解。

【正文】1. 最短路径问题的定义最短路径问题是在给定图中寻找两个节点之间最短路径的问题。

其中，节点可以表示地点，边可以表示路线或路径的长度。

最短路径的长度可以根据路径上各边的权重进行定义，常见的权重可以是边的长度、边的时间消耗等。

2. 最短路径问题的经典算法在解决最短路径问题时，有几个经典的算法可以使用。

其中，Dijkstra 算法和Bellman-Ford算法是最常用的两种算法之一。

2.1 Dijkstra算法Dijkstra算法是一种用于解决最短路径问题的贪心算法。

它以一个起始节点为出发点，逐步更新其他节点到起始节点的距离，直到找到目标节点为止。

在更新每个节点的距离时，Dijkstra算法会选择当前距离起始节点最近的节点进行更新。

通过这种方式，Dijkstra算法能够保证找到最短路径。

2.2 Bellman-Ford算法Bellman-Ford算法是一种用于解决最短路径问题的动态规划算法。

它通过多次迭代来逐步优化节点之间的距离估计值，直到收敛为止。

Bellman-Ford算法允许边的权重为负值，这使得它在一些特殊情况下具有较好的性能。

3. 最短路径问题的变形除了基本的最短路径问题，还有一些变形问题值得关注。

这些变形问题在现实生活中具有广泛的应用。

3.1 单源最短路径问题单源最短路径问题是指在给定图中，求解某个特定节点到其他所有节点的最短路径。

在实际应用中，我们可以使用Dijkstra算法或Bellman-Ford算法来解决这个问题。

初中最短路径问题总结初中最短路径问题是指在一个带权重的图中，寻找两个顶点之间的最短路径。

这个问题在实际生活中有着广泛的应用，比如在交通运输领域中寻找最短路径可以帮助我们规划最优的行车路线，提高交通效率。

在通信网络中，最短路径算法也可以帮助我们找到数据传输的最佳路径，提高网络的传输速度。

因此，了解和掌握最短路径算法对于初中生来说是非常重要的。

首先，我们来介绍最短路径算法中的两种经典算法，Dijkstra算法和Floyd算法。

Dijkstra算法是一种用于解决带权重图中单源最短路径问题的算法。

它的基本思想是从起始顶点开始，逐步扩展到所有顶点，每次选择当前距离起始顶点最近的顶点进行扩展，直到扩展到目标顶点为止。

Dijkstra算法的时间复杂度为O(V^2)，其中V为顶点数。

Floyd算法是一种用于解决带权重图中多源最短路径问题的算法。

它的基本思想是利用动态规划的思想，逐步更新顶点之间的最短路径长度，直到得到所有顶点之间的最短路径。

Floyd算法的时间复杂度为O(V^3)。

在实际应用中，我们需要根据具体的问题场景来选择合适的最短路径算法。

如果是单源最短路径问题，可以选择Dijkstra算法；如果是多源最短路径问题，可以选择Floyd算法。

除了Dijkstra算法和Floyd算法，还有一些其他的最短路径算法，比如Bellman-Ford算法、SPFA算法等。

这些算法在不同的场景下都有着各自的优势和局限性，需要根据具体的问题来选择合适的算法。

在解决最短路径问题时，我们需要注意一些常见的问题，比如负权边、负权环等。

负权边指的是图中存在权重为负数的边，而负权环指的是图中存在环路，使得环路上的边权重之和为负数。

这些情况会对最短路径算法造成影响，需要特殊处理。

总的来说，初中最短路径问题是一个重要且实用的数学问题，对于初中生来说，掌握最短路径算法有助于培养他们的逻辑思维能力和解决实际问题的能力。

通过学习最短路径算法，可以帮助他们更好地理解数学知识在实际生活中的应用，培养他们的创新意识和实践能力。

数学最短路径问题讲解数学中的最短路径问题是一个经典的优化问题，主要涉及在图或网络中找到两个节点之间的最短路径。

这类问题在日常生活和工程中有着广泛的应用，如交通路线规划、网络路由、电路设计等。

最短路径问题的常用算法有Dijkstra算法和Bellman-Ford算法。

Dijkstra算法适用于没有负权重的图，它从源节点开始，逐步找到离源节点最近的节点，直到找到目标节点。

Bellman-Ford算法则可以处理包含负权重的图，它通过不断地松弛边的权重来找到最短路径。

下面以一个简单的例子来解释最短路径问题：假设我们有一个有向图，其中节点表示城市，边表示道路，边的权重表示两城市之间的距离。

我们要找出从城市A到城市B的最短路径。

首先，我们需要理解最短路径的含义。

最短路径是指从一个节点到另一个节点经过的边的权重之和最小的路径。

如果存在负权重的边，我们需要找到一个路径，使得经过的边的权重之和加上起点的权重（如果起点有权重）最小。

在解决最短路径问题时，我们可以使用图论中的一些基本概念，如路径、权重、源节点、目标节点等。

路径是指从一个节点到另一个节点经过的一系列边，权重是指路径上边的权重之和。

源节点是指我们开始寻找最短路径的节点，目标节点是指我们要找到最短路径的终点。

最短路径问题的求解方法通常包括贪心算法和动态规划。

贪心算法是指每一步都选择当前看起来最优的选择，希望这样的局部最优选择能够导致全局最优解。

动态规划则是将问题分解为若干个子问题，并从子问题的最优解逐步推导出原问题的最优解。

在实际应用中，我们还需要考虑一些特殊情况，如图中存在负权重的环、图中存在负权重的边等。

对于这些情况，我们需要使用特定的算法来处理，如Bellman-Ford算法或Floyd-Warshall算法等。

总之，最短路径问题是一个经典的的问题，它的求解方法有很多种。

在实际应用中，我们需要根据具体情况选择合适的算法来处理最短路径问题。

arcgis 最短路径原理
ArcGIS的最短路径分析原理基于图论和网络分析的概念。

最短路径分析是指从一个地理网络的起始点到目标点寻找最短路径的过程。

最短路径分析的算法通常使用最短路径算法，其中最常用的是Dijkstra算法和A*算法。

这些算法通过计算网络中每个节点的距离和路径来确定最短路径。

最短路径分析的基本原理如下：
1. 将地理空间数据转化为网络数据，通过将响应地理要素（如街道、河流等）转化为线状要素，节点表示要素连接点。

2. 通过计算网络中各节点之间的距离和连接关系，构建网络拓扑。

3. 根据用户指定的起始点和目标点，在网络上进行搜索，并计算每个节点的最短路径距离。

4. 使用最短路径算法来计算最短路径。

Dijkstra算法根据节点之间的距离和路径成本来计算最短路径。

A*算法在Dijkstra算法的基础上加入了启发函数，以增加搜索的效率。

5. 根据计算结果，生成最短路径线状要素，以可视化显示出从起始点到目标点的最短路径。

根据用户的需求和约束条件，最短路径分析还可以考虑其他因素，如拥堵、交通规则、权重等。

这些因素可以通过网络分析工具中设置的属性或权重来体现。

总的来说，ArcGIS的最短路径分析通过构建地理网络和应用
最短路径算法，找到从起始点到目标点的最短路径，并将结果可视化表示出来。

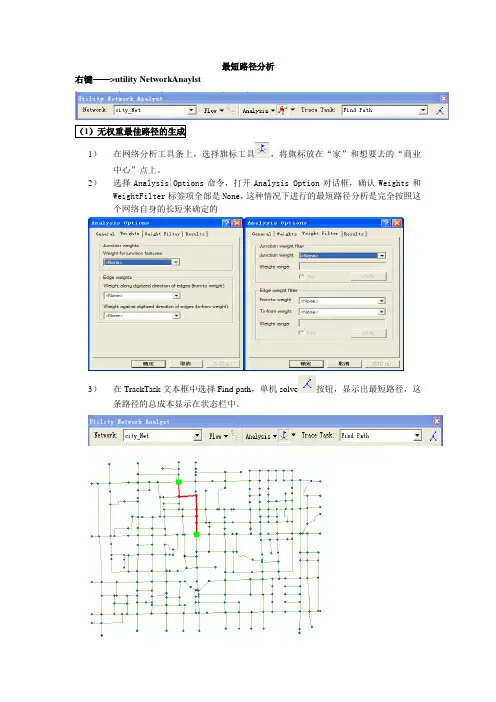
最短路径分析右键——>utility NetworkAnaylst1）在网络分析工具条上，选择旗标工具，将旗标放在“家”和想要去的“商业中心”点上。

2）选择Analysis|Options命令，打开Analysis Option对话框，确认Weights和WeightFilter标签项全部是None，这种情况下进行的最短路径分析是完全按照这个网络自身的长短来确定的3）在TrackTask文本框中选择Find path，单机solve按钮，显示出最短路径，这条路径的总成本显示在状态栏中。

1）在设施网络分析工具条上，点选旗标工具，将旗标分别放在“家”和想去的某个“商业中心”的位置上2）选择Analysis|Option命令，打开Analysis Option对话框，进入Weights标签页，在边的权重（Egdge Weights）上，全部选择长度（length）权重属性3）在Track Task文本框中选择Find Path，单击solve按钮，则以长度为比重的最短路径将显示出来，这条路径的总成本显示在状态栏中。

以上是通过距离远近的选择而得到的最佳路径。

实际中不同类型的道路由于道路车流量的问题，有时要选择通行时间最短的路径，同样可以用网络分析来获得最佳路径。

这里的时间属性是在建网之前，通过各个道路的类型（主干道，次要道等）得到速度属性，然后通过距离和速度的商值确定的。

例子里并没有考虑红灯问题以及其他因素，是一种较理想的情况，可以通过逐渐加入将其他要素来完善。

1）在设施网络分析工具条上，点选旗标工具，将旗标工具按照访问的顺序依次放在各个目标点上。

2）选择Analysis|Options命令，打开AnalysisOptions对话框，进入Weight标签页，在边的权重（EdgeWeights）上，全部选择长度（Length）权重属性3）在TrackTask文本框中选择Find Path，单击solve按钮，最短路径显示出来，这条路径的总成本显示在状态栏中。

地理信息系统导论学习笔记（17）—最小耗费路径分析和网络分析互助、共享、学习一共十八章（第一章绪论、第二章坐标系统、第三章矢量数据模型、第四章栅格数据模型、第五章GIS数据获取、第六章几何变换、第七章空间数据准确度和质量、第八章属性数据管理、第九章数据显示与地图编制、第十章数据探查、第十一章矢量数据分析、第十二章栅格数据分析、第十三章地形制图与分析、第十四章视域和流域、第十五章空间插值、第十六章地理编码和动态分段、第十七章最小耗费路径分析和网络分析、第十八章GIS模型与建模。

）本章概览最小耗费路径分析最小耗费路径分析的应用网络网络拼接网络分析本章介绍最小耗费路径分析和网络分析，两者都涉及运动和线性要素。

最小耗费路径分析是基于栅格的，且关注面较窄。

用耗费栅格定义通过每个像元所需的耗费，最小耗费路径分析能找到像元间的最小累积耗费路径。

最小耗费路径分析是很有用的，如经常作为一种分析工具，用于确定建设耗费最低（最理想）和环境影响最小的新建道路或管线。

网络分析要求矢量格式并已建立拓扑关系的网格。

地理信息系统导论学习笔记（3）最常见的网络分析可能是最短路径分析。

了解路径距离分析最小耗费路径分析介绍内容为：源栅格、耗费栅格、耗费距离量测、生成最小累积耗费路径、最小耗费路径分析的选项。

最小耗费路径分析所需要素包括：源栅格、耗费栅格、耗费距离量测和生成最小累积耗费路径的算法。

源栅格，源栅格定义了源像元。

源栅格中仅源像元有像元值，所有其他的像元都不赋值。

耗费栅格，耗费栅格定义了穿过每个像元的耗费或阻抗。

耗费栅格包含3个特征：1、每个像元的耗费通常是不同耗费的总和。

2、耗费可以是实际耗费也可以是相对耗费。

相对耗费可以分级，如分为1-5级，5为最高耗费等级。

3、耗费因素的权重由每个因素的相对重要性而定。

要组成一个耗费栅格，我们由编制和估算一个耗费变量表开始。

然后对每个耗费变量分别生成一个栅格，乘以每个耗费因素的权重，再用局部拟合运算将耗费栅格相加，其局部加和即是穿过每个像元所需的总耗费。

【初中数学】最短路径模型及例题解析一、最短路径模型简介在日常生活中，我们常常会遇到寻找从一个地点到另一个地点的最短路径问题。

例如，从家到学校、从甲地到乙地等。

在数学领域，最短路径问题属于图论的研究范畴，是图论中的一个基本问题。

最短路径模型就是用来解决这类问题的一种数学方法。

最短路径模型主要包括以下几个要素：1. 图：由顶点（地点）和边（路径）组成的集合。

2. 距离：表示两个顶点之间的距离或权重。

3. 路径：从一个顶点到另一个顶点经过的边的序列。

4. 最短路径：在所有路径中，长度最小的路径。

二、最短路径模型的求解方法1. 枚举法：枚举所有可能的路径，然后从中选择长度最小的路径。

这种方法适用于顶点数量较少的简单图。

2. Dijkstra算法：适用于带权重的有向图，通过逐步求解，找到从源点到其他所有顶点的最短路径。

3. Floyd算法：适用于求解任意两个顶点之间的最短路径，通过动态规划的方法，求解所有顶点对之间的最短路径。

三、例题解析【例题1】某城市有6个主要交通枢纽，分别用A、B、C、D、E、F表示。

下面是这6个交通枢纽之间的距离表（单位：千米）：```A B C D E FA 0 5 7 8 9 10B 5 0 6 7 8 9C 7 6 0 4 5 6D 8 7 4 0 3 4E 9 8 5 3 0 2F 10 9 6 4 2 0```求从A到F的最短路径。

【解析】这是一个典型的最短路径问题，我们可以使用Dijkstra算法求解。

1. 初始化：将所有顶点的距离设置为无穷大，源点A的距离设置为0。

2. 选取距离最小的顶点，标记为已访问。

此时，A为已访问顶点。

3. 更新相邻顶点的距离：从A出发，更新B、C、D、E、F的距离。

此时，B、C、D、E、F的距离分别为5、7、8、9、10。

4. 重复步骤2和3，直到所有顶点都被访问。

最后得到的最短路径为A→B→E→F，长度为14千米。

【例题2】某城市有5个公园，分别用P1、P2、P3、P4、P5表示。

最短路径分析可行性分析最短路径分析是一种在图形或网络中找到最短路径的技术。

这种分析方法可以应用于各种场景，如交通规划、GPS导航、电信网络、物流配送等。

在进行最短路径分析之前，我们需要先构建一个图形或网络模型，然后使用适当的算法来计算最短路径。

在进行最短路径分析之前，我们需要进行可行性分析。

可行性分析是评估和判断一个方法或决策是否可行、合理、可实施的过程。

对于最短路径分析，主要从技术可行性、经济可行性和社会可行性三个方面进行分析。

首先，技术可行性是指是否存在适当的技术和工具来进行最短路径分析。

对于小规模的网络或图形，如城市中的交通路网，使用常规算法如迪杰斯特拉或A*等算法可以很方便地求解最短路径问题。

对于大规模复杂的网络，如全球互联网或物流网络，需要使用更高级的算法和技术，如分布式计算、并行计算或机器学习等方法。

因此，在进行最短路径分析前，需要确认是否有合适的技术和工具来应用。

其次，经济可行性是指进行最短路径分析的成本是否可接受。

成本包括软件工具的费用、计算资源的费用、数据采集和处理的费用等。

通常情况下，最短路径分析需要依赖地理信息系统（GIS）等软件工具，这些工具通常需要支付一定的许可费用。

另外，进行最短路径分析可能需要大量的计算资源，包括计算机、服务器等，并且可能需要支付相应的电费、维护费用等。

此外，数据的采集和处理也需要相应的费用，如地理数据的采集和处理、电信数据的获取等。

因此，在进行最短路径分析之前，需要综合考虑是否有足够的经济资源来支持。

最后，社会可行性是指进行最短路径分析是否对社会有积极的影响。

最短路径分析常应用于交通规划、物流配送等领域，可以提高交通效率、减少交通拥堵、减少能源消耗等，对于城市和社会发展具有重要意义。

然而，最短路径分析可能会涉及个人隐私和数据安全等问题，例如GPS导航、电信网络分析可能会涉及个人位置信息、通信记录等敏感信息的收集和处理。

因此，在进行最短路径分析之前，需要充分考虑和解决相关的隐私和安全问题。

最短路径问题和解法最短路径问题是计算一个图中从一个源点到目标点的最短路径问题，是图论中的重要问题之一。

该问题的解法可以划分为两种：单源最短路径问题和全源最短路径问题。

一、单源最短路径问题单源最短路径问题是指从一个源点出发，计算该源点到其他所有点的最短路径的问题。

解法有两种：Dijkstra算法和Bellman-Ford算法。

1. Dijkstra算法Dijkstra算法是一种贪心算法，每次将到源点距离最短的点加入已求出最短路径的点集。

虽然Dijkstra算法只适用于边权值均为正的带权有向图或者无向图，但是它的时间复杂度相比Bellman-Ford算法更优秀，为O(n^2)。

2. Bellman-Ford算法Bellman-Ford算法是一种较为通用的算法，不需要图的属性满足任何特殊要求，但是时间复杂度为O(n^3)，不适用于大规模的图。

算法原理是进行n次松弛操作，查找从源点到其他点的最短路径，其中进行松弛的过程是比较消耗时间的。

二、全源最短路径问题全源最短路径问题是指求解所有点之间的最短路径问题。

解法有两种：Floyd算法和Johnson算法。

3. Floyd算法Floyd算法是一种动态规划算法，算法将所有点对之间的最短路径逐步推进，通过枚举中间点，得到更加精细的状态转移方程和最短路径。

时间复杂度为O(n^3)，因此带来的计算负担较大。

4. Johnson算法Johnson算法目前是解决稠密图最短路径问题的最好算法之一。

Johnson算法先通过引入虚拟点，将原图转化为一个没有负权边的新图，再对新图使用Dijkstra算法进行求解。

该算法的时间复杂度为O(mnlogn)，其中m为边的条数，n为点的个数。

综上所述，最短路径问题是图论中的重要问题之一。

对于单源最短路径问题，Dijkstra算法和Bellman-Ford算法是常用的解法；全源最短路径问题，Floyd算法和Johnson算法是较为常用的解法。

最短路径问题解题技巧
解决最短路径问题可以使用以下的技巧：
1. Dijkstra算法：Dijkstra算法是解决带权重有向图的单源最短
路径问题的经典算法。

它采用贪心策略，从起点开始，依次确定与起点距离最短的节点，然后通过这个节点更新与其相邻节点的距离，直到到达目标节点。

2. Bellman-Ford算法：Bellman-Ford算法是解决带负权重边的
有向图的单源最短路径问题的算法。

它采用动态规划的思想，通过多次迭代，逐步更新各个节点的最短路径。

3. Floyd-Warshall算法：Floyd-Warshall算法是解决带权重有向图的所有节点对之间的最短路径问题的算法。

它采用动态规划的思想，通过多次迭代，逐步更新各个节点对之间的最短路径。

4. A*算法：A*算法是一种启发式搜索算法，用于解决带权重
的有向图的单源最短路径问题。

它综合考虑节点的实际距离和启发函数预测的剩余距离，选择当前最有可能达到目标的节点进行搜索。

5. SPFA算法：SPFA算法是Bellman-Ford算法的一种优化版本，用于解决带负权重边的有向图的单源最短路径问题。

它采用队列来存储待更新的节点，避免了重复更新节点的操作，从而提高了算法的效率。

以上是几种常用的解决最短路径问题的算法技巧，根据具体问
题的要求和图的特征，选择适合的算法可以较好地解决最短路径问题。

初中数学最短路径问题(经典版)分析
初中数学最短路径问题的分析
最短路径问题是图论研究中的一个经典算法问题，旨在寻找图中两结点之间的最短路径。

该问题可以分为四种形式：确定起点的最短路径问题、确定终点的最短路径问题、确定起点终点的最短路径问题和全局最短路径问题。

将军饮马”、“造桥选址”和“费马点”是最短路径问题的原型。

解决该问题需要涉及一些数学知识，如“两点之间线段最短”、“垂线段最短”、“三角形三边关系”、“轴对称”和“平移”。

该问题通常涉及角、三角形、菱形、矩形、正方形、梯形、圆、坐标轴和抛物线等。

解题思路可以通过找对称点实现“折”转“直”，或者通过“三折线”转“直”等变式问题进行考查。

总之，初中数学最短路径问题是一个需要一定数学基础和思维能力的经典问题。

掌握解题思路和相关知识可以帮助学生更好地理解数学概念和培养数学思维。