高二数学 双曲线的简单性质导学案

2.2.2双曲线的几何性质（一）学习目标重难点1、掌握双曲线标准方程中a 、b 、c 、e 之间的关系；2、了解双曲线的渐近线的概念和证明；3、尝试用对比的方法分析双曲线的范围、对称性、顶点等几何性质。

重点：双曲线的几何性质难点：直线与双曲线的交点，弦长问题，用第二定义求双曲线方程一、问题引导，自我探究以双曲线标准方程12222=-by a x 为例进行说明。

1．范围：观察双曲线的草图，可以直观看出曲线在坐标系中的范围：双曲线在两条直线a x ±= 的外侧。

注意：从双曲线的方程如何验证？2．对称性： 是双曲线的对称轴， 是双曲线12222=-by a x 的对称中心，双曲线的对称中心叫做 。

3．顶点：双曲线和x 轴有两个交点是 ，他们是双曲线12222=-by a x 的顶点。

4．渐近线：他们是如何确立的？5. 叫做等轴双曲线；等轴双曲线的渐近线是 。

6.双曲线的离心率是二、探究精讲:以双曲线标准方程12222=-by a x 为例进行说明双曲线的顶点、渐近线和离心率。

1．顶点：在双曲线12222=-b y a x 的方程里，对称轴是,x y 轴，所以令0=y 得a x ±=，因此双曲线和x轴有两个交点)0,()0,(2a A a A -，他们是双曲线12222=-by a x 的顶点。

令0=x ，没有实根，因此双曲线和y 轴没有交点。

1）注意：双曲线的顶点只有两个，这是与椭圆不同的（椭圆有四个顶点）， 双曲线的顶点分别是实轴的两个端点。

2）实轴：线段2A A 叫做双曲线的实轴，它的长等于2,a a 叫做双曲线的实半轴长。

虚轴：线段2B B 叫做双曲线的虚轴，它的长等于2,b b 叫做双曲线的虚半轴长。

在作图时，我们常常把虚轴的两个端点画上（为要确定渐进线），但要注意他们并非是双曲线的顶点。

2．渐近线：注意到开课之初所画的矩形，矩形确定了两条对角线，这两条直线即称为双曲线的渐近线。

2.2.2双曲线的简单几何性质学习目标：1、通过对双曲线标准方程的讨论，把握双曲线的范围，对称性，极点，渐近线和离心率等几何性质与双曲线的中心，实轴，虚轴，渐进线，等轴双曲线的概念，加深对a 、b 、c 、e 的关系及其几何意义的明白得。

2、能利用双曲线的简单几何性质及标准方程解决相关的大体问题。

【学习重点】双曲线的简单几何性质及其应用。

【学习难点】渐近线方程的导出。

知识回忆一、双曲线的概念： 二、双曲线的标准方程：3、回忆椭圆有哪些几何性质，是如何探讨的？学习进程一、 双曲线的几何性质（一）试一试类比探讨椭圆的简单几何性质的方式，依照双曲线的标准方程22221,(0,0)x y a b a b-=>>，研究它的几何性质。

①范围 ：由双曲线的标准方程可得：=22by 从而得x 的范围： ；即双曲线在不等式 和所表示的区域内。

22ax = 从而得y 的范围为 。

②对称性：以x -代x ，方程不变，这说明因此双曲线关于 对称。

同理，以y -代y ，方程不变得双曲线关于对称，以x -代x ，且以y -代y ，方程也不变，得双曲线关于 对称。

③极点：即双曲线与对称轴的交点。

在方程12222=-by a x 里，令y=0,得x= 取得双曲线的极点坐标为1A （ ）2A （ ） ；咱们把1B （ ）2B （ ）也画在y 轴上（如图）。

线段 别离叫做双曲线的实轴和虚轴，它们的长别离为 。

④离心率：双曲线的离心率e= ，范围为 。

试探：离心率能够刻画椭圆的扁平程度，双曲线的离心率刻画双曲线的什么几何特点？探讨：在学习椭圆时，以原点为中心，2a 、2b 为邻边的矩形，关于估量仍以原点为中心，2a 、2b 为邻边作一矩形(板书图形)，那么双曲线和那个矩形有什么关系？当a 、b 为已知时，那个矩形的两条对角线的方程是什么？○5双曲线特有性质----- 双曲线22221x y a b-=的渐近线方程为 ,双曲线各支向外延伸时，与它的渐近线 ， 。

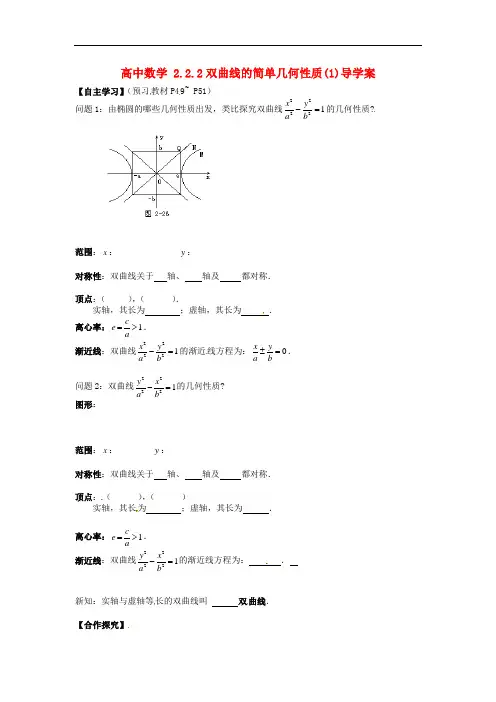
高中数学 2.2.2双曲线的简单几何性质(1)导学案 【自主学习】（预习教材P49~ P51） 问题1：由椭圆的哪些几何性质出发，类比探究双曲线22221x y a b-=的几何性质?范围：x ： y ：对称性：双曲线关于 轴、 轴及 都对称．顶点：（ ），（ ）．实轴，其长为 ；虚轴，其长为 ．离心率：1c e a=>． 渐近线：双曲线22221x y a b -=的渐近线方程为：0x y a b±=．问题2：双曲线22221y x a b-=的几何性质? 图形：范围：x ： y ：对称性：双曲线关于 轴、 轴及 都对称．顶点：（ ），（ ）实轴，其长为 ；虚轴，其长为 ．离心率：1c e a=>． 渐近线：双曲线22221y x a b-=的渐近线方程为： ．新知：实轴与虚轴等长的双曲线叫 双曲线．【合作探究】例1．（教材P51例3）求双曲线22916144y x-=的实半轴长和虚半轴长、焦点坐标、离心率、渐近线方程．例2求双曲线的标准方程：⑴实轴的长是10，虚轴长是8，焦点在x轴上；⑶渐近线方程为23y x=±，经过点9(,1)2M-．【目标检测】1．双曲线221168x y-=实轴和虚轴长分别是（）．A．8、42 B．8、22 C．4、42 D．4、22 2．双曲线224x y-=-的顶点坐标是（）．A．(0,1)± B．(0,2)± C．(1,0)± D．（2,0±）3．双曲线22148x y-=的离心率为（）．A．1 B．2 C．3D．2 4．双曲线2241x y-=的渐近线方程是．5、已知双曲线的离心率2e=(5,3)M-，求其标准方程。

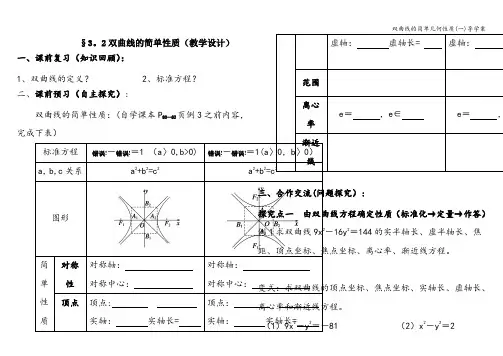
1标准方程 错误!－错误!＝1 （a 〉0,b>0) 错误!－错误!＝1(a 〉0，b 〉0） a ，b,c 关系 a 2+b 2=c 2 a 2+b 2=c 2
渐近
线
探究点二由性质求标准方程(定型→设方程→定量→作答)
例2 求满足下列条件的双曲线的标准方程:
(1)双曲线的焦点为（2，0)，右顶点为(错误!，0)； (2)实半轴长为8，离心率为错误!；
变式:求满足下列条件的双曲线方程
(1）双曲线C的焦点为（0,5)，虚轴长为4; （2）实轴长为2,离心率为2；
四、巩固提高（链接高考）：
1、（2013陕西卷）双曲线x2
16
－错误!＝1的离心率为______，两条渐近线的方程为_____．
2、(2011年高考安徽卷）双曲线2x2－y2＝8的实轴长是
3、（2011年高考江西卷）若双曲线错误!-错误!=1的离心率e=2，则m=__ __.
4、思考：若a=b，则渐近线的方程为_____，离心率e＝
五、小结(方法总结）：
（1）双曲线的简单性质（2）应用：①方程→性质②性质→方程
六、作业：1、P835 2、补充:求适合下列条件的双曲线的标准方程：
（1）焦点分别为F1（－3,0），F2（3,0)，离心率e＝ 3
（2)虚轴长为12,离心率为4
5
；。

教师学科教案[ 20 – 20 学年度第__学期]任教学科：_____________任教年级：_____________任教老师：_____________xx市实验学校2-2《双曲线的几何性质》导学案【学习目标】类比椭圆几何性质的研究方法研究双曲线：范围、对称性、顶点、渐近线、离心率，了解双曲线的第二定义.【学习难点】双曲线的几何性质【学习难点】渐进线、离心率对双曲线的影响【问题导学】1.画出双曲线)0,0(12222>>=-b a b y a x 与)0,0(12222>>=-b a bx a y 的图像.2.根据1画出的图像类比椭圆几何性质的研究方法，分别指出双曲线 )0,0(12222>>=-b a b y a x 与)0,0(12222>>=-b a bx a y 中x ，y 的范围、对称性、顶点、实轴长、实半轴长、虚轴长、虚半轴长.3.认真阅读课本，分别指出)0,0(12222>>=-b a b y a x 与)0,0(12222>>=-b a bx a y 的渐近 线的定义，求法，特征.什么是等轴双曲线？等轴双曲线有何特征？4.类比椭圆，双曲线的离心率是什么？它刻画了双曲线的什么性质？【典型例题】例1、求与双曲线2222=-y x 有公共渐近线，且过点)2,2(-M 的双曲线的标准方程.【基础题组】1．求下列双曲线的实轴、虚轴长，顶点、焦点坐标、离心率和渐近线方程．(1)4x 2－3y 2=12 (2)16x 2－9y 2=－144 328)3(22=-y x 819)4(22=-y x 8)5(22-=-y x (6)1254922-=-y x2.双曲线14322=-y x 的实轴长和虚轴长分别是( ) A . 32，4 B .4，32 C .3，4 D . 2，33．双曲线12222=-by a x (a >0，b >0)的焦点到它的渐近线的距离等于( )A . 22b a b +B .bC . aD . 22b a a + 4．如果双曲线的实半轴长为2，焦距为6，那么双曲线的离心率为( )A .23B . 26 C . 23 D .2 5．双曲线的渐近方程是x y 21±=，焦点在坐标轴上，焦距为10，其方程为( ) A . 152022=-y x B . 152022=-y x 或 152022=-x y C . 120522=-y x D . 152022±=-x y 6．已知双曲线的渐近线方程为x y 43±=，则此双曲线的 ( ) A ．焦距为10 B ．实轴长与虚轴长分别为8与6C ．离心率e 只能是45或35D ．离心率e 不可能是45或35 7．等轴双曲线的一个焦点是F 1(4，0)，则它的标准方程是_________，渐近线方程是 ______________.8.已知双曲线1222=-b y x (b >0)的一条渐近线方程为x y 2=，则b =____________ 9.已知双曲线)0,0(12222>>=-b a by a x 的离心率为2，焦点与椭圆192522=+y x 的焦点相同，那么双曲线的焦点坐标为____________，渐近线方程为____________10．若双曲线的实轴长，虚轴长，焦距依次成等差数列，则其离心率为____________11．设圆过双曲线116922=-y x 的一个顶点和一个焦点，圆心在此双曲线上，则圆心到双曲线中心的距离是 ____________12．已知双曲线191622=-y x 上一点M 到左焦点F 1的距离是它到右焦点距离的5倍，则M 点的坐标为____________13．双曲线的渐近线方程为x y ±=，两顶点之间的距离为2的标准方程：____________14．双曲线的其中一条渐近线的斜率为72，求此双曲线的离心率. 【拓展题组】15．双曲线x2b2－y2a2＝1的两条渐近线互相垂直，那么该双曲线的离心率为( )A ．2B . 3C . 2D . 3216．双曲线x29－y216＝1的一个焦点到一条渐近线的距离等于( )A . 3B ．3C ．4D ．2 17．双曲线x24＋y2b ＝1的离心率e ∈(1，2)，则b 的取值范围是________．18．椭圆x24＋y2a2＝1与双曲线x2a2－y 2＝1焦点相同，则a ＝________.19．双曲线x26－y23＝1的渐近线与圆(x －3)2＋y 2＝r 2(r >0)相切，则r ＝________. 20．已知动圆与⊙C 1：(x ＋3)2＋y 2＝9外切，且与⊙C 2：(x －3)2＋y 2＝1内切，求动圆圆心M 的轨迹方程．。

8.7《双曲线》一、学习目标（1）了解双曲线的定义、几何图形和标准方程，知道其简单的几何性质(范围、对称性、顶点、离心率、渐近线)二、知识链接1．双曲线的定义(1)定义：平面内与两个定点F1，F2的距离的差的________等于常数2a(2a______|F1F2|)的点的轨迹叫做双曲线．这两个定点叫做双曲线的________，两焦点间的距离叫做双曲线的________．※(2)另一种定义：平面内动点M到定点F的距离和它到定直线l的距离之比等于常数e(e>1)的轨迹叫做双曲线．定点F叫做双曲线的一个焦点，定直线l叫做双曲线的一条准线，常数e叫做双曲线的________．(3)实轴和虚轴相等的双曲线叫做____________．“离心率e＝2”是“双曲线为等轴双曲线”的______条件，且等轴双曲线两条渐近线互相______．一般可设其方程为x2－y2＝λ(λ≠0)．2．双曲线的标准方程及几何性质焦点在x轴上焦点在y轴上(1)图形(2)标准方程y2a2－x2b2＝1(a＞0，b＞0)(3)范围x≥a或x≤－ay≥a或y≤－a(4)中心原点O(0，0)(5)顶点A1(－a，0)，A2(a，0)(6)对称轴x轴，y轴(7)焦点F1(0，－c)，F2(0，c)(8)焦距2c＝2a2＋b2(9)离心率(10)渐近线方程y＝±abx3．与双曲线定义及标准方程相关结论(1)已知双曲线的标准方程，只要令双曲线的标准方程中右边的“1”为“0”就可得到渐近线方程，即方程x2a2－y2b2＝0就是双曲线x2a2－y2b2＝1(a＞0，b＞0)的两条渐近线方程．(2)求双曲线方程的方法以及双曲线定义和双曲线标准方程的应用都和与椭圆有关的问题相类似．因此，双曲线与椭圆的标准方程可统一为Ax2＋By2＝1的形式，当A ＞0，B ＞0，A ≠B 时为椭圆，当A ·B ＜0时为双曲线．(3)直线与双曲线交于一点时，不一定相切，如当直线与双曲线的渐近线平行时，直线与双曲线相交于一点，但不相切；反之，当直线与双曲线相切时，直线与双曲线仅有一个交点．(4)与双曲线x2a2－y2b2＝1(a ＞0，b ＞0)有共同渐近线的双曲线系方程为x2a2－y2b2＝λ(λ≠0)．4．与双曲线几何性质相关结论 (1)离心率e ＝ca＝1＋⎝ ⎛⎭⎪⎫b a 2． (2)焦点到渐近线的距离为b ．(3)通径长为2b2a．(4)P 为双曲线上一点，则|OP|≥a ，|PF1|≥c －a ，△PF1F2的面积为S ＝b2·sin θ1－cos θ＝b2tanθ2(θ＝∠F1PF2)．三、导学指导与检测导学 导学检测及课堂展示双曲线的定义及标准方程例1、(1)(2019－2020学年陕西汉中市高三上第五次质检)若双曲线E ：x 29－y 216＝1的左、右焦点分别为F 1，F 2，点P 在双曲线E 上，且|PF 1|＝7，则|PF 2|等于( )A ．1B ．13C ．1或13D ．15(2)经过点A (4，1)，且对称轴都在坐标轴上的等轴双曲线方程为________．(3)(2019哈尔滨调研)已知双曲线C 的右焦点F 与抛物线y 2＝8x 的焦点相同，若以点F 为圆心，2为半径的圆与双曲线C 的渐近线相切，则双曲线C 的方程 为 ( )A ．y 23－x 2＝1 B ．x 23－y 2＝1 C ．y 22－x 22＝1 D ．x 22－y 22＝1(4)已知圆C 1：(x ＋3)2＋y 2＝1和圆C 2：(x －3)2＋y 2＝9，动圆M 同时与圆C 1及圆C 2相外切，则动圆圆心M 的轨迹方程为________．【点拨】 ①双曲线定义的应用主要有两个方面：一是判定平面内动点的轨迹是否为双曲线，进而求出双曲线方程；二是在“焦点三角形”中常利用正弦定理、余弦定理，经常结合||PF 1|－|PF 2||＝2a ，运用平方的方法，建立与|PF 1|·|PF 2|的联系．②求双曲线的标准方程一般用待定系数法；当双曲线焦点的位置不确定时，为了避免讨论焦点的位置，常设双曲线方程为Ax 2＋By 2＝1(AB ＜0)，这样可以简化运算．变式1、(1)已知双曲线x 22－y 2＝1，点F 1，F 2为其两个焦点，点P 为双曲线上一点，若PF 1⊥PF 2，则△F 1PF 2的面积是 ( )A ．4B ．2C ．1D ．12(2)已知双曲线过点(4，3)，且渐近线方程为y ＝±12x ，则该双曲线的标准方程为________．(3)已知双曲线C 1与双曲线C 2的焦点重合，C 1的方程为x 23－y 2＝1，若C 2的一条渐近线的倾斜角是C 1的一条渐近线的倾斜角的2倍，则C 2的方程为_______________．(4)已知点M (－3，0)，N (3，0)，B (1，0)，动圆C 与直线MN 相切于点B ，分别过点M ，N 且与圆C 相切的两条直线相交于点P ，则点P 的轨迹方程为 ( )A ．x 2－y 210＝1(x ＞0) B ．x 2－y 28＝1(x ＞1)C ．x 2－y 28＝1(x ＞0) D ．x 2－y 210＝1(x ＞1)双曲线的几何性质命题角度1 渐近线例2、(1)(2019江苏卷)在平面直角坐标系xOy 中，若双曲线x 2－y 2b2＝1(b >0)，经过点(3，4)，则该双曲线的渐近线方程是________．(2)(2019届内蒙古呼伦贝尔高三模拟)已知双曲线C ：x 2a 2－y 2b2＝1(a ＞0，b ＞0)的焦距为2c ，焦点到双曲线C 的渐近线的距离为32c ，则双曲线的渐近线方程为( ) A ．y ＝±3x B ．y ＝±2x C ．y ＝±x D ．y ＝±2x【点拨】 求双曲线x 2a 2－y 2b 2＝1(a >0，b >0)或y 2a 2－x 2b 2＝1(a >0，b >0)的渐近线方程的方法是：令右边的常数等于0，即令x 2a 2－y 2b 2＝0，得y ＝±b a x ，或令y 2a 2－x 2b 2＝0，得y ＝±abx ．反之，已知渐近线方程为y ＝±b a x ，可设双曲线方程为x 2a 2－y 2b2＝λ(a >0，b >0，λ≠0)．变式2、(1)(2020届东北师大附中高三第五次模拟)已知双曲线x 2a 2－y 2b2＝1(a >0，b >0)的离心率为2，则该双曲线的渐近线方程为 ( )A ．x ±y ＝0B ．x ±3y ＝0C ．3x ±y ＝0D ．2x ±y ＝0(2)(2019届辽宁沈阳省示范协作校高三一模)设F 1和F 2为双曲线x 2a 2－y 2b2＝1(a ＞0，b ＞0)的两个焦点，若F 1，F 2，A (0，2b )是正三角形的三个顶点，则双曲线的渐近线方程是( )A ．y ＝±33x B ．y ＝±3x四、巩固诊断 A 层1、判断下列命题是否正确，正确的在括号内画“√”，错误的画“×”．(1)平面内到两定点的距离的差等于常数(小于两定点间距离)的点的轨迹是双曲线． ( ) (2)平面内到点F 1(0，2)，F 2(0，－2)的距离之差的绝对值等于4的点的轨迹是双曲线． ( )(3)方程x 2m －y 2n＝1(mn >0)表示焦点在x 轴上的双曲线． ( )(4)等轴双曲线的渐近线互相垂直，离心率等于2． ( )(5)设P 是双曲线x 216－y 220＝1上一点，F 1，F 2分别是双曲线的左、右焦点，若|PF 1|＝9，则|PF 2|等于1或17． ( )2、(2019浙江卷)渐近线方程为x ±y ＝0的双曲线的离心率是 ( )A ．22B ．1C ． 2D ．2 3、已知双曲线x 2a －3＋y 22－a＝1，焦点在y 轴上，若焦距为4，则a 等于 ( )A ．32B ．5C ．7D ．124、(2020天津卷)设双曲线C 的方程为x 2a 2－y 2b2＝1(a >0，b >0)，过抛物线y 2＝4x 的焦点和点(0，b )的直线为l ．若C 的一条渐近线与l 平行，另一条渐近线与l 垂直，则双曲线C 的方程为 ( )A ．x 24－y 24＝1 B ．x 2－y 24＝15、已知双曲线C ：x 2a 2－y 2b2＝1(a >0，b >0)的离心率e ＝2，且它的一个顶点到相应焦点的距离为1，则双曲线C 的方程为_______________．B 层1．(2020届陕西汉中高三上五检)方程x 2m ＋2＋y 2m －3＝1表示双曲线，则m 的取值范围为 ( )A ．(－3，0)B ．(－1，3)C ．(－3，4)D ．(－2，3)2．(2020届天津市河西区高三二模)已知双曲线的一个焦点与抛物线x 2＝20y 的焦点重合，且双曲线上的一点P 到双曲线的两个焦点的距离之差的绝对值等于6，则该双曲线的标准方程为 ( )A ．x 29－y 216＝1B ．x 216－y 29＝1C ．y 29－x 216＝1 D ．y 216－x 29＝1 3．(2019届天津市河北区高三一模)在平面直角坐标系中，过点(22，－2)且渐近线方程为y ＝±2x 的双曲线的标准方程为 ( )A ．x 24－y 22＝1B ．x 27－y 214＝1 4．已知双曲线y 2m 2－x 2n 2＝1(m >0，n >0)的渐线方程为y ＝±23x ，则此双曲线的离心率为 ( )A ．134 B ．132 C ．133 D ．1345．(2020－2021学年湖南衡阳八中高二上10月考)若双曲线x 2a2－3y 2＝12的离心率为2，则其渐近线方程为 ( )A ．y ＝±33x B ．y ＝±3x C ．y ＝±13x D ．y ＝±3x 6．(2020年福建厦门高二下期末质检)已知双曲线E ：x 24－y 212＝1的左、右焦点分别为F 1，F 2，P 是E 的右支上一点，则下列结论中不正确的是 ( )A ．|PF 1|－|PF 2|＝4B ．E 的离心率是2C ．|PF 1|的最小值是6D ．P 到两渐近线的距离的乘积是2 37．(2020赣榆智贤中学高三模拟)在平面直角坐标系xOy 中，已知双曲线C 的渐近线方程为y ＝±x ，且它的一个焦点为F (2，0)，则过双曲线C 的一个顶点且垂直于x 轴的直线与两条渐近线所成的三角形的面积为________．8．已知双曲线C ：x 2a 2－y 2b2＝1(a >0，b >0)的离心率为3，点(3，0)是双曲线的一个顶点．(1)求双曲线的方程；(2)经过双曲线右焦点F 2作倾斜角为30°的直线，直线与双曲线交于不同的两点A ，B ，求|AB |． C 层9．()设F1和F2为双曲线－＝1(a ＞0，b ＞0)的两个焦点，若F1，F2，A(0，2b)是正三角形的三个顶点，则双曲线的渐近线方程是 ( )A ．y ＝±x B．y ＝±x C ．y ＝±x D．y ＝±x 10．()已知A ，B 两监测点间的距离为800 m ，且A 监测点听到爆炸声的时间比B 监测点迟2 s ，设声速为340 m/s ，下列说法正确的是 ( )①爆炸点在以A ，B 为焦点的椭圆上；②爆炸点在以A ，B 为焦点的双曲线的一支上；③若B 监测点的声强是A 监测点的4倍(声强与距离的平方成反比)，则爆炸点到B 监测点的距离为 m ； ④若B 监测点的声强是A 监测点的4倍(声强与距离的平方成反比)，则爆炸点到B 监测点的距离为680 m ．A ．①③ B．②④ C．①④ D．②③ 11．()设双曲线C ：－＝1(a>0，b>0)的左、右焦点分别为F1，F2，离心率为．P 是C 上一点，且F1P⊥F2P．若△PF1F2的面积为4，则 a ＝ ( )A ．1B ．2C ．4D ．812．()设F 为双曲线C ：－＝1(a ＞0，b ＞0)的右焦点，O 为坐标原点，以OF 为直径的圆与圆x2＋y2＝a2交于P ，Q 两点．若|PQ|＝|OF|，则C 的离心率为 ( )A ．B ．C ．2D ．13．已知双曲线过点(3，－2)且与椭圆4x2＋9y2＝36有相同的焦点． (1)求双曲线的标准方程．(2)若点M 在双曲线上，F1，F2是双曲线的左、右焦点，且|MF1|＋|MF2|＝6，试判断△MF1F2的形状．五、堂清、日清记录今日之事今日毕 日积月累成大器。

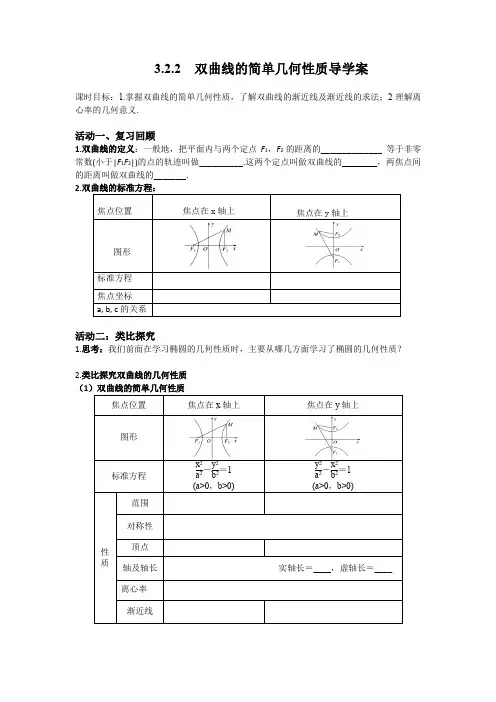
3.2.2 双曲线的简单几何性质导学案课时目标：1.掌握双曲线的简单几何性质，了解双曲线的渐近线及渐近线的求法；2理解离心率的几何意义.活动一、复习回顾1.双曲线的定义：一般地，把平面内与两个定点F 1，F 2的距离的______________ 等于非零常数(小于|F 1F 2|)的点的轨迹叫做_________ .这两个定点叫做双曲线的________，两焦点间的距离叫做双曲线的_______ .2. 焦点位置 焦点在x轴上 焦点在y 轴上图形标准方程 焦点坐标a, b, c 的关系活动二：类比探究1.思考：我们前面在学习椭圆的几何性质时，主要从哪几方面学习了椭圆的几何性质？2.类比探究双曲线的几何性质 （1焦点位置焦点在x 轴上焦点在y 轴上图形标准方程x 2a 2－y 2b 2＝1 (a>0，b>0)y 2a 2－x 2b 2＝1 (a>0，b>0)性质范围对称性顶点轴及轴长 实轴长＝____，虚轴长＝____离心率渐近线（2）重、难点突破：双曲线的渐近线渐近线方程：____________________ 渐近线方程：____________________（3）思考归纳：结合双曲线的离心率与渐近线斜率的关系总结出离心率的几何意义.活动三：练习巩固例. 求双曲线 229-16=144y x 的顶点坐标、焦点坐标、实轴长、虚轴长、离心率及渐近线方程.活动四：课堂小结1.知识清单：双曲线的几何性质：范围、对称性、顶点、渐近线及离心率；结论1：渐近线方程为：y =±ba x (焦点在x 轴上)或y =±ab x （焦点在y 轴上）. 结论2：离心率越大，双曲线开口越___ ；离心率越小，开口越___.2.数学思想方法归纳： 类比、数形结合等.3.常见误区：忽略焦点位置致错.活动五：作业布置课后思考：设双曲线方程为22(0)x y k k R k -=∈≠且，求该双曲线的渐近线方程与离心率，并观察该双曲线有什么特点？。

2.3.2《双曲线的简单几何性质》导学案【学习目标】1.通过方程，研究曲线的性质.理解双曲线的范围、对称性及对称轴，对称中心、离心率、顶点、渐近线的概念；2.掌握双曲线的标准方程、会用双曲线的定义解决实际问题；3.掌握双曲线的渐近线的求法. 【导入新课】 复习导入1.复习椭圆的几何性质，重点复习它的范围、对称性、离心率、和有关量，类比得到双曲线的有关性质；2. 双曲线的标准方程及其推导过程. 新授课阶段双曲线的简单几何性质①范围：由双曲线的标准方程得，222210y x b a=-≥，进一步得：x a ≤-，或x a ≥．这说明双曲线在不等式 所表示的区域；②对称性：由以x -代x ，以y -代y 和x -代x ，且以y -代y 这三个方面来研究双曲线的标准方程发生变化没有，从而得到双曲线是以 为对称轴， 为对称中心；③顶点：圆锥曲线的顶点的统一定义，即圆锥曲线的对称轴与圆锥曲线的交点叫做圆锥曲线的顶点．因此双曲线有两个顶点，由于双曲线的对称轴有实虚之分，焦点所在的对称轴叫做 ，焦点不在的对称轴叫做 ；④渐近线：直线 叫做双曲线22221x y a b-=的渐近线；⑤离心率： 双曲线的焦距与实轴长的比 叫做双曲线的离心率（1e >）． 例1双曲线方程为2221x y -=，则它的右焦点坐标为（ ）A.0⎫⎪⎪⎝⎭B.0⎫⎪⎪⎝⎭C.0⎫⎪⎪⎝⎭D.)【解析】例2求与双曲线221169x y -=共渐近线，且经过()3A -点的双曲线的标准方及离心率． 解：【点评】这个要进行分类讨论，但只有一种情形有解，事实上，可直接设所求的双曲线的方程为()22,0169x y m m R m -=∈≠. 例3 已知双曲线C :12222=-by a x (0,0)a b >>，B 是右顶点,F 是右焦点, 点A 在x 轴正半轴上，且满足 OA OB OF ||、||、||成等比数列,过F 作双曲线C 在第一、三象限的渐近线的垂线l ，垂足为P . （1）求证：⋅=⋅；（2）若l 与双曲线C 的左、右两支分别相交于点D 、E ，求双曲线C 的离心率e 的取值范围. 解：1.双曲线的几何性质的灵活运用；2.双曲线的渐近线的求法及其运用. 作业见同步练习部分 拓展提升1．双曲线1322=-y x 的渐近线中，斜率较小的一条渐近线的倾斜角是（ ） Ａ．060 Ｂ．090 Ｃ．0120 Ｄ．01502．如果221||21x y k k+=---表示焦点在y 轴上的双曲线，那么它的半焦距C 的取值范围是（ ） A ．(1,＋∞) B ．（0，2） C ．(2,＋∞) D ．（1，2）3．已知对称轴为坐标轴的双曲线的一条渐近线为x －2y =0，则该双曲线的离心率为（ ）A 或 5B 或 3CD ．54 或54．过点（－7，－6 2 ）与（27 ，－3）的双曲线标准方程为 .5．已知F 1，F 2是双曲线22221x y a b-=（a ＞0,b ＞0)的左、右两个焦点，点P 在双曲线右支上，O 为坐标原点，若△POF 2是面积为1的正三角形，则b 的值是 .6． 设双曲线的一个焦点为F ，虚轴的一个端点为B ，如果直线FB 与该双曲线的一条渐近线垂直，那么此双曲线的离心率为( )A. 2B. 3C.3＋12 D.5＋127． 已知双曲线x 2－y 23＝1的左顶点为A 1，右焦点为F 2，P 为双曲线右支上一点，则PA 1→·PF 2→的最小值为( )A ．－2B ．－8116C ．1D ．0 8． 双曲线x 216－y 29＝1上到定点(5,0)的距离是9的点的个数是( )A ．0B ．2C ．3D ．49． 双曲线2x 2－3y 2＝1的渐近线方程是________.10．在平面直角坐标系中，双曲线Γ的中心在原点，它的一个焦点坐标为(5,0)，e 1＝(2,1)、e 2＝(2，－1)分别是两条渐近线的方向向量．任取双曲线Γ上的点P ，若OP →＝a e 1＋b e 2(a 、b ∈R )，则a 、b 满足的一个等式是________.11．双曲线的渐近线为y ＝±43x ，则双曲线的离心率为________.12．点M (x ，y )到定点F (5,0)距离和它到定直线l ：x ＝95的距离的比是53，(1)求点M 的轨迹方程；(2)设(1)中所求方程为C ，在C 上求点P ，使|OP |＝34(O 为坐标系原点).13．已知双曲线的中心在原点，离心率为2，一个焦点F (－2,0) .(1)求双曲线方程；(2)设Q 是双曲线上一点，且过点F 、Q 的直线l 与y 轴交于点M ，若|MQ →|＝2|QF →|，求直线l 的方程.参考答案新授课阶段双曲线的简单几何性质x a ≤-，或x a ≥ x 轴和y 轴，原点 实轴，虚轴；b y x a =±ac e = 例1【解析】双曲线的222131,,,22a b c c ====.【答案】C 例2解：根据双曲线221169x y -=的渐近线方程为34y x =±. ① 焦点在x 轴上时，设所求的双曲线为22221169x y k k-=， ∵()3A -点在双曲线上，∴214k =-，无解； ② 焦点在y 轴上时，设所求的双曲线为22221169x y k k -+=， ∵()3A -点在双曲线上，∴214k =， 因此，所求双曲线的标准方程为221944y x -=，离心率53e =. 【点评】这个要进行分类讨论，但只有一种情形有解，事实上，可直接设所求的双曲线的方程为()22R,0169x y m m m -=∈≠. 例3 解：（1）法一．:()al y x c b=--， (),,a y x c bb y x a ⎧=--⎪⎪⎨⎪=⎪⎩解得2(,).a ab P c c |OA → |,|OB → |,|OF → |成等比数列，PA →=（0，－ab c）法二：同上得2(,).a ab P c c0.PA x PA OP PA FP PA OF PA OP PA FP ∴⊥⋅-⋅=⋅=∴⋅=⋅轴．． （2）222222(),,a y x c bb x a y a b ⎧=--⎪⎨⎪-=⎩422222244422222222422221242244222222)2()0,()0,.,.2a b x x c a b b a a a c b x cx a b b b b a c a b b x x a b bb a b ac a a e e ∴--=-+-+=-+⋅=<-∴>>->∴>>（）．即（即．即 拓展提升1．C 【解析】求出倾斜角的正切值. 2．A 【解析】解不等式组.3．A 【解析】由a,b 之间的关系转化成a,c 之间的关系.4．2212575x y -=【解析】待定系数法. 5． 2 【解析】数形结合.6．D 【解析】设双曲线的方程为x 2a 2－y 2b 2＝1，设F (c,0)，B (0，b )，直线FB 的斜率为－bc ，与其垂直的渐近线的斜率为b a ，所以有－b 2ac ＝－1，即b 2＝ac ，所以c 2－a 2＝ac ，两边同时除以a 2可得e 2－e －1＝0，解得e ＝1＋52. 22222222(,),(,),,..a ab b ab OP FP c c c ca b a b PA OP PA FP c cPA OP PA FP ==-∴⋅=-⋅=-∴⋅=⋅7．A [解析] 由已知可得A 1(－1,0)，F 2(2,0)，设点P 的坐标为(x ，y )，则PA 1→·PF 2→＝(－1－x ，－y )·(2－x ，－y )＝x 2－x －2＋y 2，因为x 2－y 23＝1 (x ≥1)，所以PA 1→·PF 2→＝4x 2－x －5，当x ＝1时，PA 1→·PF 2→有最小值－2.故选A.8．C [解析] (5,0)是双曲线的右焦点，它到双曲线左顶点的距离为9，所以以(5,0)为圆心，以9为半径作圆，该圆与双曲线的右支有两个交点，所以共有3个这样的点. 9．y ＝±63x [解析] 双曲线2x 2－3y 2＝1的渐近线方程为2x ±3y ＝0，即y ＝±63x . 10．4ab ＝1 [解析] 易知双曲线Γ的方程为x 24－y 2＝1，设P (x 0，y 0)，又e 1＝(2,1)，e 2＝(2，－1)，由OP →＝a e 1＋b e 2，得(x 0，y 0)＝a (2，1)＋b (2，－1)，即(x 0，y 0)＝(2a ＋2b ，a －b )， ∴x 0＝2a ＋2b ，y 0＝a －b ， 代入x 24－y 2＝1整理得4ab ＝1.11.53或54 [解析] 当焦点在y 轴上时，a b ＝43，即9a 2＝16b 2＝16(c 2－a 2)，解得e ＝54；当焦点在x 轴上时，b a ＝43，即16a 2＝9b 2＝9(c 2－a 2)，解得e ＝53.12．[解答] (1)|MF |＝x －2＋y 2，点M 到直线l 的距离d ＝⎪⎪⎪⎪⎪⎪x －95，依题意，有x －2＋y2⎪⎪⎪⎪⎪⎪x －95＝53， 去分母，得3x －2＋y 2＝|5x －9|，平方整理得x 29－y 216＝1，即为点M 的轨迹方程．(2)设点P 坐标为P (x ，y )， 由|OP |＝34得x 2＋y 2＝34，解方程组⎩⎪⎨⎪⎧x 29－y 216＝1，x 2＋y 2＝34，得⎩⎨⎧x ＝32，y ＝4或⎩⎨⎧x ＝－32，y ＝－4或⎩⎨⎧x ＝－32，y ＝4或⎩⎨⎧x ＝32，y ＝－4，∴点P 为(32，4)或(－32，－4)或(－32，4)或(32，－4).13．解：(1)由题意可设所求的双曲线方程为x 2a 2－y 2b 2＝1(a >0，b >0)，则有e ＝ca＝2，c ＝2，所以a ＝1，则b ＝3，所以所求的双曲线方程为x 2－y 23＝1 .(2)因为直线l 与y 轴相交于M 且过焦点F (－2,0)，所以l 的斜率一定存在，设为k ，则l ：y ＝k (x ＋2)， 令x ＝0，得M (0,2k )，因为|MQ →|＝2|QF →|且M 、Q 、F 共线于l ， 所以MQ →＝2QF →或MQ →＝－2QF →. 当MQ →＝2QF →时，x Q ＝－43，y Q ＝23k ，所以Q 的坐标为⎝ ⎛⎭⎪⎫－43，23k ， 因为Q 在双曲线x 2－y 23＝1上，所以169－4k 227＝1，所以k ＝±212，所以直线l 的方程为y ＝±212(x ＋2)，当MQ →＝－2QF →时，同理求得Q (－4，－2k )代入双曲线方程得， 16－4k 23＝1，所以k ＝±352，所以直线l 的方程为y ＝±352(x ＋2) . 综上：所求的直线l 的方程为y ＝±212(x ＋2)或y ＝±352(x ＋2).。

课题 双曲线的简单性质学习目标 ：1.把握双曲线的简单几何性质.2.了解双曲线的渐近性及渐近线的概念.3.能区别椭圆与双曲线的性质．4.利用双曲线的方程研究其图象和几何性质，在自主探讨合作交流中通过类比，分析双曲线的几何性质．学习重点：把握双曲线的简单几何性质学习难点：能区别椭圆与双曲线的性质学习方式：以讲学稿为依托的探讨式教学方式。

学习进程一、课前预习指导： 1、双曲线的性质：类比椭圆的几何性质，结合图象，你能取得双曲线x 2a 2－y 2b2＝1 (a >0，b >0)的哪些几何性质？问题探讨一 双曲线的几何性质例1 求双曲线9y 2－4x 2＝－36的极点坐标、核心坐标、实轴长、虚轴长、离心率和渐近线方程．学后检测1求双曲线25y 2－4x 2＋100＝0的半实轴长，半虚轴长，核心坐标，极点坐标，离心率，渐近线方程．例2、 火力发电厂的冷却塔的外形是由双曲线绕其虚轴所在直线旋转所取得的曲面。

已知塔的总高度为150m ，塔顶的直径为70m ，塔的最小直径为67m ，喉部标高，求双曲线的标准方程。

学后检测2 求知足以下条件的双曲线方程：(1)以2x ±3y ＝0为渐近线，且通过点(1,2)；(2)离心率为54，半虚轴长为2；（3)与椭圆x 2＋5y 2＝5共核心且一条渐近线方程为y －3x ＝0.三、当堂检测1．双曲线2x 2－y 2＝8的实轴长是 ( )A ．2B ．2 2C ．4D ．4 22．双曲线3x 2－y 2＝3的渐近线方程是 ( )A ．y ＝±3xB ．y ＝±13xC ．y ＝±3xD ．y ＝±33x3．双曲线x 24－y 212＝1的核心到渐近线的距离为 ( )A ．2 3B ．2 D ．14．过双曲线x 2a 2－y 2b 2＝1(a >0，b >0)的右极点A 作斜率为－1的直线，该直线与双曲线的两条渐近线的交点别离为B ，C .假设AB →＝12BC →，那么双曲线的离心率是 ( )5．已知双曲线x 22－y 2b 2＝1 (b >0)的左，右核心别离为F 1，F 2，其一条渐近线方程为y ＝x ，点P (3，y 0)在该双曲线上，那么PF 1→·PF 2→等于 ( ) A ．－12 B ．－2 C ．0 D ．4四、课堂小结五、课后作业六．板书设计七．教（学）后反思。