下载文档原格式
一块无限大平板（如图3所示），其一半厚度为L=0.1m，初始温度T0=1000℃，突然将其插入温度T∞=20℃的流体介质中。
平板的导热系数λ=34.89W/m℃，密度ρ=7800kg/m3，比热c=0.712J/kg℃，平板与介质的对流换热系数为h=233W/m2.℃，求平板内各点的温度分布。
3．1 数学描述由于平板换热关于中心线是对称的，仅对平板一半区域进行计算即可。
坐标x的原点选在平板中心线上，因而一半区域的非稳态导热的数学描述为：(3-1)(3-2)(3-3)(3-4)该数学模型的解析解为:（3-5）其中,为方程的根，。
表3给出了在平板表面(x=L)处由式(3-5)计算得到的不同时刻的温度值。
表3 平板表面各不同时刻温度值。
时间1 2 3 4 5 6 7 8 9 10 （S）温度(℃) 981.84 974.47 968.88 964.20 960.11 956.14 953.08 949.97 947.07 944.34 3．2 数值离散3．3．1 计算区域的离散一维非稳态导热指的是空间坐标是一维的。
若考虑时间坐标，则所谓的一维非稳态导热实际上是二维问题(见图4)，即：有时间坐标τ和空间坐标x两个变量。
但要注意，时间坐标是单向的，就是说，前一时刻的状态会对后一时刻的状态有影响，但后一时刻的状态却影响不到前一时刻，图4示出了以x和τ为坐标的计算区域的离散，时间从τ=0开始，经过一个个时层增加到K时层和K+1时层。
3．3．2 微分方程的离散对于i节点，在K和K+1时刻可将微分方程(3-1)写成下面式子：(3-6)(3-7)将式(3-6)~(3-7)的左端温度对时间的偏导数进行差分离散为：(3-9)(3-8)观察式(3-8)和(3-9)，这两个式子的右端差分式完全相同，但在两个式子中却有不同含义。
对式(3-8)，右端项相对i点在K时刻的导数是向前差分。
而在式(3-9)中，右端项是I点在K+1时刻的导数的向后差分。
第三章 非稳态导热(unsteady state conduction)物体的温度随时间而变化的导热过程称非稳态导热。
0≠τ∂∂t，任何非稳态导热过程必然伴随着加热或冷却过程。
根据物体内温度随时间而变化的特征不同，非稳态导热过程可分为两类：（1）周期性导热（periodic unsteady conduction ）：物体的温度按照一定的周期发生变化； 如建筑物的外墙和屋顶温度的变化。
（2）瞬态导热(transient conduction)：物体的温度随时间不断升高或降低，在经历相当长时间后，物体的温度逐渐趋于周围介质的温度，最终达到热平衡。
分析非稳态导热的任务：找出温度分布和热流密度随时间和空间的变化规律。
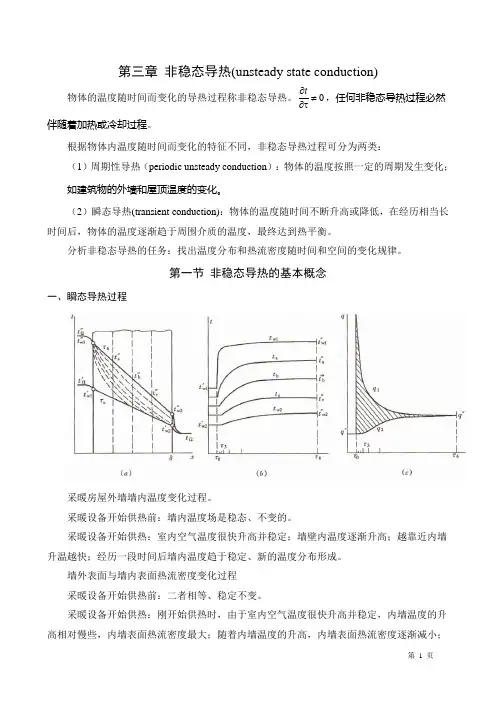
第一节 非稳态导热的基本概念一、瞬态导热过程采暖房屋外墙墙内温度变化过程。
采暖设备开始供热前：墙内温度场是稳态、不变的。
采暖设备开始供热：室内空气温度很快升高并稳定；墙壁内温度逐渐升高；越靠近内墙升温越快；经历一段时间后墙内温度趋于稳定、新的温度分布形成。
墙外表面与墙内表面热流密度变化过程 采暖设备开始供热前：二者相等、稳定不变。
采暖设备开始供热：刚开始供热时，由于室内空气温度很快升高并稳定，内墙温度的升高相对慢些，内墙表面热流密度最大；随着内墙温度的升高，内墙表面热流密度逐渐减小；随着外墙表面的缓慢升高，外墙表面热流密度逐渐增大；最终二者相等。
上述非稳态导热过程，存在着右侧面参与换热与不参与换热的两个不同阶段。
（1）第一阶段（右侧面不参与换热）是过程开始的一段时间，特点是：物体中的一部分温度已经发生变化，而另一部分仍维持初始状态时的温度分布（未受到界面温度变化的影响），温度分布显现出部分为非稳态导热规律控制区和部分为初始温度区的混合分布，物体内各处温度随时间的变化率是不一样的，即：在此阶段物体温度分布受t分布的影响较大，此阶段称非正规状况阶段或初始阶段（initialregime）。
（2）第二阶段（右侧面参与换热）当右侧面参与换热以后，物体中的温度分布不受t影响，主要取决于边界条件及物性。
非稳态导热㈠分离变量法在一维非稳态导热问题中的应用一、无限大平壁一维非稳态导热（参考文献[1]PP45-50）大平壁在等温介质中的冷却：常物性、无内热源、第三类边界条件（见图1）。
图1令：ftt-=θ，导热微分方程为：0,22φππτδθτθxxa∂∂=∂∂初始条件为：()x fx=≤≤=θδτ,0,0；边界条件：δδθθλτδθτ====∂∂-==∂∂=xxxhxxxx|,0,|,0,0φφ假设解的形式为()()()ττθΓ•=xXx,则两个常微分方程：方程(3—2—3)的解是由下表知，特征方程（3-2-4）的为()()xAxXmmmεcos=，特征值为方程()λδεεhmm=tan的正根，范数()()()[]λλεδλεεhhhNmmm+++=222221则根据()[]()mLm NdxxfAβ⎰⨯=0特征函数，得待定常数为：，其中，εδβ=二、半无限大物体一维非稳态导热（参考文献[2]PP40-45）常物性、无内热源、第二、三类边界条件典型问题：一半无限大物体，∞≤≤x 0，初始温度为F (x)，当时间τ＞0时，x ＝0的边界上以对流方式向温度为零度的介质传输热量，如图2所示。
该问题的数学描述为：三、多维的齐次问题（参考文献[2]PP49-57）典型问题：矩形截面的柱体，为二维非稳态导热，材料为常物性，物体内没有内热源，边界条件如图3所示。
τ∂∂=∂∂+∂∂ta yt x t 12222， 0,00,0,0042=+∂∂====+∂∂==∂∂=t H ytb y t y t H xta x x t x 时，时，时，时， ，()y x F t ,0==时，τ 图3矩形截面柱体的二维非稳态导热令()()()()τθΓ=y Y x X y x t ,,，分离方程如下：,0,0022=+====+''X H dxdX a x A dxdX x X X ）（β， 0,0,0042=+====+''Y H dy dY b x B Y y Y Y ）（γ， ()()()C e τγβατ22+-=Γ上述问题的完全解为：()()()()τγβαγβτ22,,,,11n m e y Y x X C y x t n m m mn n +-∞=∞=∑∑=求解待定系数C mn 后，得：()()()()()()()()()y d x d y x F y Y x X e y Y x X N N y x t a bn m n m m n nm n m ''''''=⎰⎰∑∑+-∞=∞=0011,,,,,1,,22γβγβγβττγβα 上式中出现的本征函数、本征值及范数可从表1-2中直接查得，即：()()x x X m m ββcos ,=，()()222222221H H a H N mm m +++=βββ，且m β为方程()2tan H a m m =ββ的正根：()()y y X n n γγsin ,=，()()nnnn n n H H b H N +++=222221γγγ，且n γ为方程()4cot H b n n -=γγ的正根：()()()()()()()()()y d x d y x F y x y x HHb H H Ha H e y x t a x by n m n m nnnn n mm m n n m ''''''⨯⨯++++++=⎰⎰∑∑='='+-∞=∞=002222222222211,sin cos sin cos 4,,22γβγβγγββττγβα四、某些非齐次或非线性问题的处理思路1、线性、齐次多维非稳态热传导问题（参考文献[2]PP57-61）对线性、齐次多维非稳态热传导问题，可以象一维问题那样，用分离变量法求解，其结果必定是二重或三重级数，不便于计算和应用。
