第7章 Huckel分子轨道理论
- 格式:ppt
- 大小:9.01 MB
- 文档页数:75
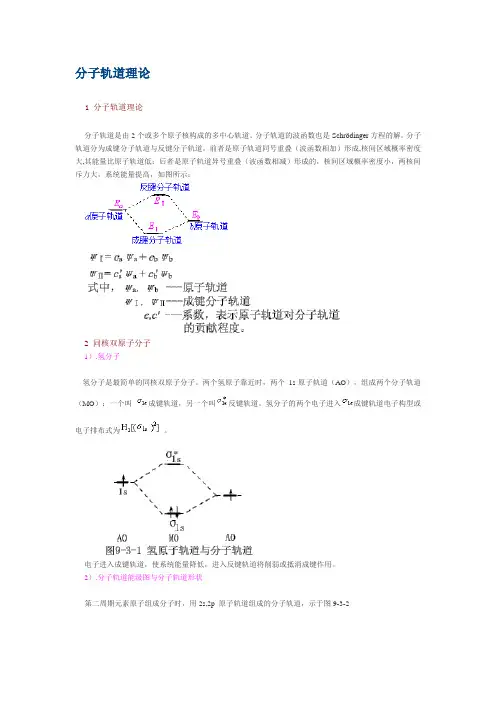
分子轨道理论1 分子轨道理论分子轨道是由2个或多个原子核构成的多中心轨道。
分子轨道的波函数也是Schrödinger方程的解。
分子轨道分为成键分子轨道与反键分子轨道,前者是原子轨道同号重叠(波函数相加)形成,核间区域概率密度大,其能量比原子轨道低;后者是原子轨道异号重叠(波函数相减)形成的,核间区域概率密度小,两核间斥力大,系统能量提高,如图所示:2 同核双原子分子1).氢分子氢分子是最简单的同核双原子分子。
两个氢原子靠近时,两个1s原子轨道(AO),组成两个分子轨道(MO):一个叫成键轨道,另一个叫反键轨道。
氢分子的两个电子进入成键轨道电子构型或电子排布式为。
电子进入成键轨道,使系统能量降低,进入反键轨道将削弱或抵消成键作用。
2).分子轨道能级图与分子轨道形状第二周期元素原子组成分子时,用2s,2p 原子轨道组成的分子轨道,示于图9-3-2由图可见,分子轨道的数目等于用于组合原子轨道数目。
两个2s原子轨道组成两个分子轨道和,6个2p原子轨道组成6个分子轨道,其中两个是σ分子轨道(和)4个是π分子轨道(两个和两个)。
相应的原子轨道及分子轨道的形状如图下所示。
由图可见:●成键轨道中核间的概率密度大,而在反键轨道中,则核间的概率密度小。
●一对2p z 原子轨道以“头碰头”方式组合形成分子轨道,时,电子沿核间联线方向的周围集中;一对2p x(2p y)原子轨道以“肩并肩”方式组合形成分子轨道,时,电子分布在核间垂直联线的方向上。
3).氧分子O2共有16个电子,O2的电子构型:O2分子有两个自旋方式相同的未成对电子,这一事实成功地解释了O2的顺磁性。
O2中对成键有贡献的是(σ2p)2和(π2p)4这3 对电子,即是一个σ键和两个π键。
O2的两个π键是三电子π键,反键轨道中的一个电子削弱了键的强度,一个三电子π键相当于半个键,故O2的叁键实际上与双键差不多。
4).氮分子N2的分子轨道能级图与O2比较,只是在和的相互位置有区别。


什么是分子轨道理论
分子轨道理论(Molecular Orbital Theory,简称MO理论)是1932年由美国化学家马利肯(R.S.Mulliken)及德国物理学家洪特(F.Hund)提出的一种描述多原子分子中电子所处状态的方法。
该理论认为原子形成分子后,电子不再属于个别的原子轨道,而是属于整个分子的分子轨道,分子轨道是多中心的。
分子轨道由原子轨道组合而成,形成分子轨道时遵从能量近似原则、对称性一致(匹配)原则、最大重叠原则,即通常说的“成键三原则”。
在分子中电子填充分子轨道的原则也服从能量最低原理、泡利不相容原理和洪特规则。
以上信息仅供参考,建议查阅化学专业书籍文献或咨询化学专业人士获取更全面更准确的信息。








分⼦轨道理论分⼦轨道理论同核双原⼦分⼦如您所知,电⼦在原⼦中存在于不同能级(例如1s,2s,3d等)的轨道中。
这些轨道表⽰在原⼦周围任何地⽅找到电⼦的概率分布。
分⼦轨道理论提出了这样⼀个概念,即分⼦中的电⼦同样存在于不同的轨道中,这使⼈们有可能在分⼦周围的特定点找到电⼦。
为了产⽣分⼦的轨道集,我们将分⼦中键合原⼦的价原⼦波函数加在⼀起。
这并不像听起来那样复杂。
让我们考虑同核双原⼦分⼦中分⼦式A 2的键合。
也许我们能想到的最简单的分⼦是氢H 2。
正如我们已经讨论过的,要产⽣氢每个氢的分⼦轨道,我们将价原⼦波函数加在⼀起以产⽣氢的分⼦轨道。
H 2中的原⼦仅具有1s轨道,因此我们将两个1s波函数相加。
正如您在原⼦结构研究中所了解的那样,原⼦波函数可以具有正或负相位-这意味着波函数y的值可以为正或为负。
有两种添加波函数的⽅法:同相(正负两个)或异相(正负另⼀个)。
展⽰了如何将原⼦波函数加在⼀起以产⽣分⼦轨道。
图%:两个1s轨道结合形成键和反键MO同相重叠组合(中的顶部轨道)在两个原⼦核之间产⽣电⼦密度的累积,从⽽导致该轨道的能量较低。
占据s H-H轨道的电⼦代表H 2的Lewis结构的电⼦键对,并适当地称为键分⼦轨道。
产⽣的另⼀个分⼦轨道s * HH显⽰原⼦核之间的电⼦密度降低,在存在节点平⾯的原⼦核之间的中点达到零值。
由于s * HH轨道显⽰出两个原⼦核之间键合的减少,这被称为反键分⼦轨道。
由于原⼦核之间电⼦密度的降低,抗键合轨道的能量⾼于键合轨道和氢1s轨道。
在分⼦H 2,没有电⼦占据反键轨道。
中总结这些关于键,反键和原⼦轨道的相对能量的发现,我们可以构建⼀个轨道相关图,如下所⽰:图%:氢的轨道相关图请注意,分离的原⼦的轨道写在图的两侧,是⽔平线,其⾼度表⽰它们的相对能量。
每个原⼦轨道上的电⼦⽤箭头表⽰。
在图的中间,写下了感兴趣分⼦的分⼦轨道。
虚线将母原⼦轨道与⼦分⼦轨道连接起来。
通常,键合分⼦轨道的能量低于其母原⼦轨道中的任何⼀个。
休克尔轨道法的分子图一、化学家休克尔E.Erich Armand Arthur Josephckel (1896~)联邦德国物理化学家。
1896年8月9日生于柏林夏洛腾堡。
1914年入格丁根大学攻读物理。
曾中断学习,在格丁根大学应用力学研究所研究空气动力学。
1918年重新攻读数学和物理,1921年在P.德拜的指导下获博士学位。
他在格丁根大学工作两年,曾任物理学家M.玻恩的助手。
1922年在苏黎世工业大学再度与德拜合作,任讲师。
1930年在斯图加特工业大学任教。
1937年任马尔堡大学理论物理学教授。
休克尔主要从事结构化学和电化学方面的研究。
他1923年和德拜一起提出强电解质溶液理论,推导出强电解质当量电导的数学表达式。
1931年提出了一种分子轨道的近似计算法即休克尔分子轨道法(HMO 法),主要用于π电子体系。
他在30年代还对芳香烃的电子特性在理论上作出了解释,并总结出:环状共轭多烯化合物中π电子数符合4n+2(n为1,2或3)者,具有芳香性。
二、休克尔分子轨道法(HMO法)的来源分子轨道理论在处理分子时,并不引进明显的价键结构的概念。
它强调分子的整体性,认为分子中的原子是按一定的空间配置排列起来的,然后电子逐个加到由原子实和其余电子组成的“有效”势场中,构成了分子。
并将分子中单个电子的状态函数称为分子轨道,用波函数ψ(x,y,z)来描述。
每个分子轨道ψi都有一个确定的能值Ei 与之相对应,Ei近似地等于处在这轨道上的电子的电离能的负值,当有一个电子进占ψi 分子轨道时,分子就获得Ei的能量。
分子轨道是按能量高低依次排列的。
参与组合的原子轨道上的电子则将按能量最低原理、鲍里不相容原理和洪特规则进占分子轨道。
根据电子在分子轨道上的分布情况,可以计算分子的总能量。
π键实际上是持有电子的围绕参与组合的原子实的π分子轨道。
1931年,休克尔提出了一种计算π分子轨道及其能值的简单方法,称为休克尔分子轨道法(即HMO 法)。
分子轨道理论的基本要点→分子轨道的概念分子轨道的概念分子轨道理论的基本要点在介绍分子轨道理论的基本要点之前,首先了解一下分子轨道的概念。
通过原子结构理论的学习,我们知道原子中的电子是处于原子核及其它电子所形成的势场中运动的,每个电子都具有一定的空间运动状态和能量。
原子中存在着若干种空间运动状态ψ、ψ、ψ……,这些空间运动状态俗称原子轨道,即原子中存在1s、2s、2p……等原子轨道。
分子轨道理论设想,在多原子分子中,组成分子的每个电子并不属于某个特定的原子,而是在整个分子的范围内运动。
分子中的电子处于所有原子核和其它电子的作用之下,分子中电子的空间运动状态也可以用波函数来描述,这些波函数俗称分子轨道,即分子中电子的空间运动状态叫分子轨道(Molecular orbit),简称MO。
正如原子中存在对应能量的若干原子轨道一样,在分子中也存在对应一定能量的若干分子轨道。
像原子结构那样遵循“能量最低原理”将分子中所有电子依次填入各分子轨道中,则可得到分子的电子构型,并由此说明分子的性质,这就是分子轨道理论的基本思路。
现将其要点介绍如下。
分子轨道理论的基本要点→分子轨道理论的基本要点★★分子轨道的概念分子轨道理论的基本要点1.分子轨道是由原子轨道线性组合而成(linear combination of atomic orbital,简称LCAO),n个原子轨道组合成n个分子轨道。
在组合形成的分子轨道中,比组合前原子轨道能量低的称为成键分子轨道,用ψ表示;能量高于组合前原子轨道的称为反键分子轨道,用ψ表示。
例如两个氢原子的1s原子轨道ψA与ψB线性组合,可产生两个分子轨道:ψ=C1(ΨA+ΨB)ψ=C2(ψA-ψB)(式中C1、C2为常数)2.原子轨道组合成分子轨道时,必须遵循对称性原则、能量近似原则和最大重叠原则。
(1) 对称性原则(对称性匹配)原子轨道均具有一定的对称性,例如s轨道是球形对称,p轨道对中心是反对称(即一半是正,一半是负),d轨道有中心对称和对坐标轴或某个平面对称。