下载文档原格式
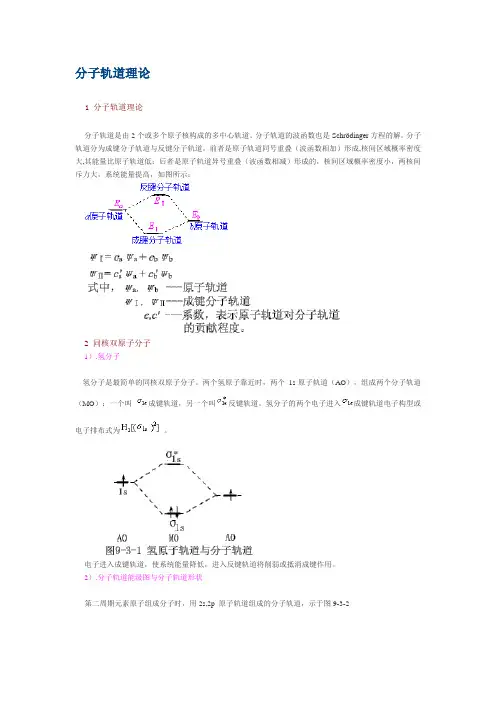
分子轨道理论1 分子轨道理论分子轨道是由2个或多个原子核构成的多中心轨道。
分子轨道的波函数也是Schrödinger方程的解。
分子轨道分为成键分子轨道与反键分子轨道，前者是原子轨道同号重叠（波函数相加）形成,核间区域概率密度大,其能量比原子轨道低；后者是原子轨道异号重叠（波函数相减）形成的，核间区域概率密度小，两核间斥力大，系统能量提高，如图所示：2 同核双原子分子1）.氢分子氢分子是最简单的同核双原子分子。
两个氢原子靠近时，两个1s原子轨道（AO），组成两个分子轨道（MO）：一个叫成键轨道，另一个叫反键轨道。
氢分子的两个电子进入成键轨道电子构型或电子排布式为。
电子进入成键轨道，使系统能量降低，进入反键轨道将削弱或抵消成键作用。
2）.分子轨道能级图与分子轨道形状第二周期元素原子组成分子时，用2s,2p 原子轨道组成的分子轨道，示于图9-3-2由图可见，分子轨道的数目等于用于组合原子轨道数目。
两个2s原子轨道组成两个分子轨道和，6个2p原子轨道组成6个分子轨道，其中两个是σ分子轨道（和)4个是π分子轨道（两个和两个）。
相应的原子轨道及分子轨道的形状如图下所示。
由图可见：●成键轨道中核间的概率密度大，而在反键轨道中，则核间的概率密度小。
●一对2p z 原子轨道以“头碰头”方式组合形成分子轨道，时，电子沿核间联线方向的周围集中；一对2p x(2p y)原子轨道以“肩并肩”方式组合形成分子轨道，时，电子分布在核间垂直联线的方向上。
3）.氧分子O2共有16个电子，O2的电子构型：O2分子有两个自旋方式相同的未成对电子，这一事实成功地解释了O2的顺磁性。
O2中对成键有贡献的是(σ2p）2和(π2p)4这3 对电子，即是一个σ键和两个π键。
O2的两个π键是三电子π键，反键轨道中的一个电子削弱了键的强度，一个三电子π键相当于半个键，故O2的叁键实际上与双键差不多。
4）.氮分子N2的分子轨道能级图与O2比较，只是在和的相互位置有区别。
第十八章分子轨道理论简介一、教学目的和要求（1）了解分子轨道理论的原理。
（1）了解周环反应的一般规律。
（2）了解分子轨道对称守恒原理在有机合成中的作用。
二、教学重点与难点分子轨道理论的原理，周环反应的理论。
三、教学方法和教学学时1、教学方法：以课堂讲授为主，结合必要的课堂讨论。
教学手段以板书和多媒体相结合。
2、教学学时：2学时四、教学内容第一节电环化反应第二节环加成反应第三节σ迁移反应第四节周环反应的理论一、电环化反应机理二、环加成反应机理三、σ键迁移反应机理五、课后作业、思考题习题：1、2、4、6、11。
§18-1 周环反应的理论一、周环反应前面各章讨论的有机化学反应从机理上看主要有两种，一种是离子型反应，另一种是自由基型反应，它们都生成稳定的或不稳定的中间体。
还有另一种机理，在反应中不形成离子或自由基中间体，而是由电子重新组织经过四或六中心环的过渡态而进行的。
这类反应表明化学键的断裂和生成是同时发生的，它们都对过渡态作出贡献。
这种一步完成的多中心反应称为周环反应。
周环反应：反应中无中间体生成，而是通过形成过渡态一步完成的多中心反应。
反应物——→产物周环反应的特征：（1） 多中心的一步反应，反应进行时键的断裂和生成是同时进行的（协同反应）。
例如：（2） 反应进行的动力是加热或光照。
不受溶剂极性影响，不被酸碱所催化，不受任何引发剂的引发。
（3） 反应有突出的立体选择性，生成空间定向产物。
例如：二、周环反应的理论 （一） 轨道和成键周环反应的过程，广泛的应用轨道来描述，这些轨道往往是用图形来表示。
有机化学中涉及最多的原子轨道为1p 轨道和2s 轨道。
原子轨道线形组合成分子轨道。
当两个等价原子轨道组合时，总是形成两个新的分子轨道，一个是能量比原子轨道低的成键轨道，另一个是能量比原子轨道高的反键轨道。
（二）分子轨道对称守恒原理原子轨道组合成分子轨道时，遵守轨道对称守恒原理。
即当两个原子轨道的对称性相同（位相相同）的则给出成键轨道，两个原子轨道的对称性不同（位相不同）的则给出反键轨道。
第三节分子轨道理论（MOT ）、概述要点：A、配体原子轨道通过线性组合，构筑与中心原子轨道对称性匹配的体群轨道。
B、中心原子轨道与配体群轨道组成分子轨道。
C、电子按照能量由低到高的顺序，依次排在分子轨道中。
形成LCAO-MO 的三原则：、ABn 型分子构筑分子轨道的方法1、步骤1）列出中心原子A 及配位原子B 中参与形成分子轨道的原子轨道；2）将B 原子轨道按等价轨道集合分类（由对称操作可彼此交换的轨道称为等价轨道）；3）将每一等价轨道集合作为表示的基，给出表示；再将其分解为不可约表示；4）用每一组等价轨道集合构筑出对应于上一步所求出的不可约表示的配体群轨道；5）将对称性相同的 配体群轨道 与中心原子轨道组合得分子轨道。
道能级分裂）1）A 原子用 ns 、每个 B 原子用 3 个 p （p x 、p y 、p z ）轨道， 共 27 个轨道形成分子轨道。
* 坐标系选择及配体编号、金属与配体间 σ道（ d 轨np 、（n-1）d 9 个轨道，5z左手坐标系；B、每个B 原子上三个p 轨道各用个向量表示，方向指向波函数正值方向；C、规定p z 向量指向中心原子，则p x、p y 向量应存在于垂直于p z 向量的平面内；D、规定第一个B 原子的p x 向量与y 轴平行（* 方向相同），则该B 原子的p y 向量应与z轴平行（*同）；E、其余（6-1）个B 原子的p x 和p y 向量的方向由O h 群对称性决定。
2）O h 群将B 原子的18 个轨道分为如下等价轨道的集合：I 、 6 个p z 轨道（可用于形成σ 分子轨道）II 、12 个p x 或p y 轨道（可用于形成π 分子轨道）3）以上述轨道集合I 为基，得出在O h群中的表示，并进行约化：4）求出与中心原子价轨道相关的配体群轨道（用投影算符）：1g 6(p z1+p z2+p z3+p z4+p z5+p z6)中心原子轨道s1g1(2p z5+2p z6-p z1-p z2-p z3-p z4)d z212(p z1-p z2+p z3-p z4)d x2-y2 u 12(p z1-p z3)p x21(p z2-p z4)p y21(p z5-p z6)p zσ = A1g + E g + T1u配体群轨道示意图：yy z zxyyxd x 2 2yzzzzyyxxxsψA1g22-yd z2ψT1u(x)ψ E g(z2) p xp y ψ T 1u(y) p z ψT1u(z)3、配合物的σ分子轨道能级图1)σ分子轨道能级图MO (AO 2)2)d 轨道能级分裂np ns (n-1)dt 1u *a 1g * e g *t2ge gt1u a1gAO 1MO* (AO 1)AO 2中心原子轨道 群轨道分子轨道配体σ对于许多配体如 H 2O 、NH 3、F -等，配体 p z 轨道能级低于金属轨道能四、金属与配体间 π分子轨道（ 强、 弱场配合物 ）1． 配体 π群轨道构筑 p x ，p y ，p z已用于形成 σ分子轨道B 原子用于形成 π 分子轨道的原子1）形成 π分子轨道的原子轨道E g ：d x 2-y 2，d z 2A 1g ：s T 1u：只剩余 T 2g ：d xy ，d xz ，d yz轨道集合： 12 个 p x 或 p y 轨道。
分子轨道理论及基态与激发态分子轨道理论基本概念一、分子轨道：(molecular orbital) 描述分子中电子运动的波函数，指具有特定能量的某电子在相互键合的两个或多个原子核附近空间出现的概率最大的区域。
分子轨道由原子轨道线性组合而成。
二、成键三原则：能量相近、最大重叠、对称性匹配。
只有对称性相同的两个原子轨道才能组成分子轨道。
σ对称：一个原子轨道，取X轴作为对称轴，旋转180°，轨道符号不变。
如S，Px，d x2-y2为σ对称。
π对称：一个原子轨道，取X轴作为对称轴，旋转180°，轨道符号改变。
Py，Pz，d xy是π对称。
由σ对称的原子轨道组成的键——σ键由π对称的原子轨道组成的键——π键三、成键轨道与反键轨道分子轨道与原子轨道的联系：轨道守恒——2个原子轨道线性组合，产生2个分子轨道；能量守恒——2个分子轨道的总能量等于2个原子轨道的总能量；能量变化——每个分子轨道的能量不同于原子轨道的能量组合结果—定会出现能量高低不同的两个分子轨道。
——这是原子轨道线性组合的方式不同所致。
波函数同号的原子轨道相重叠，原子核间的电子云密度增大，形成的分子轨道的能量比各原子轨道能量都低，成为成键分子轨道。
波函数异号的原子轨道相重叠，原子核间的电子云密度减小，形成的分子轨道的能量比各原子轨道能量都高，成为反键分子轨道。
四、电子填入分子轨道时服从以下原则：1、能量最低原理：电子在原子或分子中将优先占据能量最低的轨道。
2、保利不相容原理：在同一原子或分子中、同一轨道上只能有两个电子，且自旋方向必须相反。
3、洪特规则：在能量相同的轨道中（简并轨道），电子将以自旋平行的方式、分占尽可能多的轨道基态与激发态当分子中的所有电子都遵从构造原理的这三个原则时，分子所处的最低能量状态——基态。
通常情况下，分子处于基态。
激发态：当分子获取能量后，分子中的电子排布不完全遵从构造原理，分子处于能量较高的状态——激发态，是原子或分子吸收一定的能量后，电子被激发到较高能级但尚未电离的状态。
第三节分子轨道理论（MOT ）、概述要点：A、配体原子轨道通过线性组合，构筑与中心原子轨道对称性匹配的体群轨道。
B、中心原子轨道与配体群轨道组成分子轨道。
C、电子按照能量由低到高的顺序，依次排在分子轨道中。
形成LCAO-MO 的三原则：、ABn 型分子构筑分子轨道的方法1、步骤1）列出中心原子A 及配位原子B 中参与形成分子轨道的原子轨道；2）将B 原子轨道按等价轨道集合分类（由对称操作可彼此交换的轨道称为等价轨道）；3）将每一等价轨道集合作为表示的基，给出表示；再将其分解为不可约表示；4）用每一组等价轨道集合构筑出对应于上一步所求出的不可约表示的配体群轨道；5）将对称性相同的 配体群轨道 与中心原子轨道组合得分子轨道。
道能级分裂）1）A 原子用 ns 、每个 B 原子用 3 个 p （p x 、p y 、p z ）轨道， 共 27 个轨道形成分子轨道。
* 坐标系选择及配体编号、金属与配体间 σ道（ d 轨np 、（n-1）d 9 个轨道，5z左手坐标系；B、每个B 原子上三个p 轨道各用个向量表示，方向指向波函数正值方向；C、规定p z 向量指向中心原子，则p x、p y 向量应存在于垂直于p z 向量的平面内；D、规定第一个B 原子的p x 向量与y 轴平行（* 方向相同），则该B 原子的p y 向量应与z轴平行（*同）；E、其余（6-1）个B 原子的p x 和p y 向量的方向由O h 群对称性决定。
2）O h 群将B 原子的18 个轨道分为如下等价轨道的集合：I 、 6 个p z 轨道（可用于形成σ 分子轨道）II 、12 个p x 或p y 轨道（可用于形成π 分子轨道）3）以上述轨道集合I 为基，得出在O h群中的表示，并进行约化：4）求出与中心原子价轨道相关的配体群轨道（用投影算符）：1g 6(p z1+p z2+p z3+p z4+p z5+p z6)中心原子轨道s1g1(2p z5+2p z6-p z1-p z2-p z3-p z4)d z212(p z1-p z2+p z3-p z4)d x2-y2 u 12(p z1-p z3)p x21(p z2-p z4)p y21(p z5-p z6)p zσ = A1g + E g + T1u配体群轨道示意图：yy z zxyyxd x 2 2yzzzzyyxxxsψA1g22-yd z2ψT1u(x)ψ E g(z2) p xp y ψ T 1u(y) p z ψT1u(z)3、配合物的σ分子轨道能级图1)σ分子轨道能级图MO (AO 2)2)d 轨道能级分裂np ns (n-1)dt 1u *a 1g * e g *t2ge gt1u a1gAO 1MO* (AO 1)AO 2中心原子轨道 群轨道分子轨道配体σ对于许多配体如 H 2O 、NH 3、F -等，配体 p z 轨道能级低于金属轨道能四、金属与配体间 π分子轨道（ 强、 弱场配合物 ）1． 配体 π群轨道构筑 p x ，p y ，p z已用于形成 σ分子轨道B 原子用于形成 π 分子轨道的原子1）形成 π分子轨道的原子轨道E g ：d x 2-y 2，d z 2A 1g ：s T 1u：只剩余 T 2g ：d xy ，d xz ，d yz轨道集合： 12 个 p x 或 p y 轨道。
以其为基求出表示，并约化：π = T 1g +T 2g +T 1u +T 2u用投影算符构筑 π群轨道：12g2 (p y 1+p x 5+p x 3+p y 6) 21(p x 2+p y 5+p y 4+p x 6)2)t 2g π群轨道图形中心原子轨道21(p x 1+p y 2+p y 3+p x 4)dxyyx+ yxt 1g群轨道的配体（如（无 f 轨道 ） （无g 轨道）t1uπ分子轨道（强 +非键轨道： σ分子轨道 ）++ _2、配合物的 配合物） 1）具有低能充满 π（p x ，p y ，p z 已形成H2O、X )o t e2*g g（金属）t2g 群轨道t2（g 配体）△o减小，为弱场配合物。
2）具有高能空π群轨道的配体（如Ph3P)t 2g （金属）eg△o 增大，为强场配合物。
3、分子轨道理论的应用 1）解释光谱化学系列r < Cl < F < OH < H 2O < NH 3 <NO 2 < CN 、CO 、PR 3t 2*g （配体）t2g 群轨道egot2ge g *π 电子提供者π电子接受者弱π键提供者电子e*got 2*g （金属）t2g 群轨道t 2（g 配体） e gt 2*g （配体）t2g 群轨道t2g （金属）eg3） 解释配合物的磁性强σ电子提供者FeSO 4.7H 2O=5.10 B.M.e*ge *go t 2goe g *K 4[Fe(CN) 6] μ=0.00 B.M.t1e g e gt2gt t2g群轨道2g e g t1u a1gt1u*a1g*t2g*e g*t2ge g*t2g群轨道t2ge gt1ua1g五、晶体场理论与分子轨道理论的比较1、相同之处:：1）都可得到d 轨道能级分裂的结果；2）都可对配合物的磁性给予解释。
2、区别：1) t2g、e g轨道的性质不同CFT ：t2g、e g为纯原子轨道；MOT ：不考虑π成键时，八面体配合物中t2g虽可看作是原子轨道，但e g*中包含了配体群轨道的成分。
t1np ns(n-1)dt e1g ua1gCFT 2)d 轨道能级分裂原因不同 MOT 认为是原子轨道组合成分子轨道所致认为是由于中心原子轨道与配体静电场相互作用所致e*gt 2ge *g t 2*gt 2gt2g 群轨道e ge*g(n-1)dMOTt 1*ua 1g *np ns4) 对配合物稳定性的解释不同定配合物稳定性的主要因素CFT 认为，配合物稳定性是由中心离子与配体间静电相互吸引贡献。
配体的对孤对电子进入成键分子轨道释放的能量是决t 1u a 1g22 d x -yd xyt 2g e gt 1a 1g *np nse*ge g t 1a1g(n-1)d-z--+ +--x x-y############################################## #######第四节 角重叠模型对于配合物的化学键理论， MO 理论可以得出好 的结果。
但 MO 计算量大。
近年来又发展了角重叠模 1、AOM 是一种简易的仍然把焦点集中于 MO 法；2、AOM 比 CFT 更详细和优越，但不是完整的 MO 法；3、AOM 体现了金属与配体相互作用的主要特征，是 理解配合物结构、磁性和光谱的成功模型；4、AOM 可估计配体轨道的稳定化作用及金属 d 轨道 的不稳定作用。
． 基本原理型（AMO ），使问题简化，计算量小。
d 轨道的E＊dz2yoz y若保持 r 不变，旋转Φ轨道至 （θ, 位φ置），则双原子 重叠积分dz 2xo +能量变化值 e σ=βσS σ2（可由量子化学原理导出） βσ—轨道间相互作用强度的量度，和 d z 2与Φ轨 道能量间隔成反比；S σ―d z 2与Φ轨道的标准双原子重叠积分yS = [1/4(1+3cos2 θσ=)] SF σSσ 角重叠因子F σ=1/4(1+3cos2 θ)ΔEσ=βσS2 = Fσ2βσSσ2 =Fσ2e对于π键: 同理ΔEπ=Fπ2eπ (eπ=βπSπ2)；Sπ—标准双原子π重叠积分z量变化若中心原子d 轨道与n 个配体相互作用，则总的能nE ( E E ) i二、中心离子d轨道能级的变化1、中心离子d轨道与配体轨道的角重叠因子：Fπyd z2d xyd x2-y2FσFπx1/4(1+3cos2 θ)1/231/2/2sinφsin2 θ31/2/2cosφsin2 θ31/2/4sin2 φ -(c1os2θ ) 1/231/2/4cos2φ(-1cos2θ)2、常见配体位置Fσ2及Fπ2的计算结构位置结构位置直线5，6 三角双锥1, 5, 6, 7, 8 平面三角形1，7，8 四方锥1, 2, 3, 4, 5平面正方形1，2，3，4 八面体1, 2, 3, 4, 5, 63/40 0 00 10 3/40 0 010 03/4 0 03 0 π 1π1 π1π1含一个 σ和两个 π轨道的配体在某些位置的 F λ2值配体位置d z 21/4金属离子 d 轨道d x 2-y 2d yz1/41/4 3/4 1/4 012/96 σ1 0 0 0π0 0 1 1 01/4 3/16 0 0 71/49/10 3/4 1/4 3/48 1/4 3/16 0 09/11/49 σ0 0 1/30 3/4 1/4 3/42/3 2/3 2/9101/3 1/32/31/32/3 2/92/9 2/911 1/31/3 1/32/3 2/3 2/92/92/92/9121/3π2/91/3 1/32/32/92/3 2/9根据该表的数据，可以很容易计算出何构型中的能量变化。
3、能量计算：1) 八面体Δ E(d z2) = (1/4+1/4+1/4+1/4+1+1)eσ= 3eσΔ E(d x2-y2) = (3/4+3/4+3/4+3/4) eσ= 3eσ同理：ΔE(d xz) = Δ E(y d z) = Δ E(x d y) =eσ。
eπ>0，配体为强π电子供给者；eπ~0，配体为弱π电子供给者；eπ<0，配体为强π电子接受者。
且有三种情况：因此π键对分裂能影响有两种情况：e g* (3e σ) e g* (3eσ)分裂能Δo = 3eσ- 4e2）四面体：Δ E(2t) = (1/3+1/3+1/3+1/3)eσ +4/3eσ+8/9eπΔE(e )= (2/3+2/3+2/3+2/3)eπ= 8/3eπΔt = 4/3eσ+ 8/9eπ- 8/3eπ= 4/9(3eσ- 4eπ) = 4/9 Δo3）平面正方形：Δted 轨道弱场Δot2g* (4eπ)d 轨道Δot2g* (4eπ)强场(2/9+2/9+2/9+2/9)eπ=4、电子的排布成键的σ分子轨道能量较接近于配体的σ轨道，因而配体的孤对电子将进入这些成键轨道；而中心离子的d 电子将进入反键轨道。
若有π键结合：ΔE (d x2-y2) = (3/4 + 3/4 + 3/4 + 3/4)eσ= 3eσΔ E(d xy) = (1/4+1/4+1/4+1/4)eσ= eσΔ E(d z2) = (1+1+1+1)eπ = 4eπΔE(d xz) = Δ E(y d z) = (1+1)eπ = 2eπ(2eπ)d x2-y2 (3eσ)eσ与4eπ大小决定。
