线性规划习题及答案
- 格式:doc
- 大小:695.00 KB
- 文档页数:5

简单线性规划复习题及答案(1)1、设,x y 满足约束条件⎪⎩⎪⎨⎧≤--≥-+≥-020202y x y x y x ,则22y x ++的最大值为 452、设变量,x y 满足⎪⎩⎪⎨⎧≥-+≥-≤-+030201825y x y x y x ,若直线20kx y -+=经过该可行域,则k 的最大值为答案:13、若实数x 、y ,满足⎪⎩⎪⎨⎧≤+≥≥123400y x y x ,则13++=x y z 的取值范围是]7,43[.4、设y x z +=,其中y x ,满足⎪⎩⎪⎨⎧≤≤≤-≥+k y y x y x 0002,若z 的最大值为6,则z 的最小值为5、已知x 、y 满足以下条件220240330x y x y x y +-≥⎧⎪-+≥⎨⎪--≤⎩,则22z x y =+的取值范围是 4[,13]56、已知实数,x y 满足约束条件1010310x y x y x y +-≤⎧⎪-+≥⎨⎪--≤⎩,则22(1)(1)x y -+-的最小值为 127、已知,x y 满足约束条件1000x x y x y m -≥⎧⎪-≤⎨⎪+-≤⎩,若1y x +的最大值为2,则m 的值为 58、表示如图中阴影部分所示平面区域的不等式组是⎪⎩⎪⎨⎧≥-+≤--≤-+0623063201232y x y x y x9、若曲线y = x 2上存在点(x ,y )满足约束条件20,220,x y x y x m +-≤⎧⎪--≤⎨⎪>⎩,则实数m 的取值范围是 (,1)-∞10、已知实数y ,x 满足10103x y x y y -+≥⎧⎪+-≤⎨⎪≥-⎩,则3z x y =+的最小值为 -311、若,x y 满足约束条件10,0,40,x x y x y -≥⎧⎪-≤⎨⎪+-≤⎩则x y的最小值为 13. 12、已知110220x x y x y ≥⎧⎪-+≤⎨⎪--≤⎩,则22(2)(1)x y ++-的最小值为___10_13、已知,x y 满足不等式0303x y x y x -≥⎧⎪+-≥⎨⎪≤⎩,则函数3z x y =+取得最大值是 1214、已知x ,y 满足约束条件⎪⎩⎪⎨⎧≤≥+≥+-3005x y x y x ,则z =2x +4y 的最小值是-615、以原点为圆心的圆全部在区域⎪⎩⎪⎨⎧≥++≤-+≥+-0943042063y x y x y x 内,则圆面积的最大值为 π51616、已知y x z k y x x y x z y x 42,0305,,+=⎪⎩⎪⎨⎧≥++≤≥+-且满足的最小值为-6,则常数k = 0 . 17、已知,x y 满足约束条件,03440x x y y ≥⎧⎪+≥⎨⎪≥⎩则222x y x ++的最小值是 118、在平面直角坐标系中,不等式组0,0,,x y x y x a +≥⎧⎪-≥⎨⎪≤⎩(a 为常数),表示的平面区域的面积是8,则2x y +的最小值 14-19、已知集合22{(,)1}A x y x y =+=,{(,)2}B x y kx y =-≤,其中,x y R ∈.若A B ⊆,则实数k 的取值范围是⎡⎣20、若x ,y 满足⎩⎪⎨⎪⎧x +y -2≥0,kx -y +2≥0,y ≥0,且z =y -x 的最小值为-4,则k 的值为 12-21、若实数x ,y 满足不等式组201020x y x y a -≤⎧⎪-≤⎨⎪+-≥⎩,目标函数2t x y =-的最大值为2,则实数a 的值是 222、已知点(,)P x y 满足条件020x y x x y k ≥⎧⎪≤⎨⎪++≤⎩,若3z x y =+的最大值为8,则实数k = 6- .23、设实数x , y 满足的最大值是则x y y y x y x ,03204202⎪⎩⎪⎨⎧≤->-+≤-- 23.24、已知实数y x , 22222)(y x y y x +++的取值范围为 ⎥⎦⎤⎢⎣⎡+221,35.简单线性规划复习题及答案(2)1、设实数x,y 满足⎪⎩⎪⎨⎧≤-≥-+≤--0205202y y x y x 则y x x y z +=的取值范围是 10[2,]3由于yx表示可行域内的点()x y ,与原点(00),的连线的斜 率,如图2,求出可行域的顶点坐标(31)(12)A B ,,,, (42)C ,,则11232OA OB OC k k k ===,,,可见123y x ⎡⎤∈⎢⎥⎣⎦,,结合双勾函数的图象,得1023z ⎡⎤∈⎢⎥⎣⎦,,2、若实数,x y 满足不等式组22000x y x y m y ++≥⎧⎪++≤⎨⎪≥⎩,且2z y x =-的最小值等于2-,则实数m 的值等于 1-3、设实数x 、y 满足26260,0x y x y x y +≤⎧⎪+≤⎨⎪≥≥⎩,则{}max 231,22z x y x y =+-++的取值范围是 [2,9]【解析】作出可行域如图,当平行直线系231x y z +-=在直线BC 与点A 间运动时,23122x y x y +-≥++,此时[]2315,9z x y =+-∈,平行直线线22x y Z ++=在点 O 与BC 之间运动时,23122x y x y +-≤++,此时,[]222,8z x y =++∈. ∴[]2,9z ∈图23 A yxOcB 634、佛山某家电企业要将刚刚生产的100台变频空调送往市内某商场,现有4辆甲型货车和8辆乙型货车可供调配。
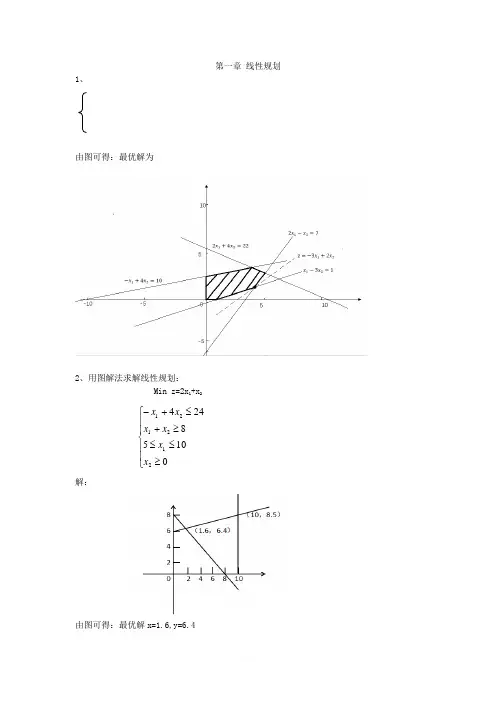
第一章 线性规划1、由图可得:最优解为2、用图解法求解线性规划: Min z=2x 1+x 2⎪⎪⎩⎪⎪⎨⎧≥≤≤≥+≤+-01058244212121x x x x x x解:由图可得:最优解x=1.6,y=6.4Max z=5x 1+6x 2⎪⎩⎪⎨⎧≥≤+-≥-0,23222212121x x x x x x解:由图可得:最优解Max z=5x 1+6x 2, Max z= +∞Maxz = 2x 1 +x 2⎪⎪⎩⎪⎪⎨⎧≥≤+≤+≤0,5242261552121211x x x x x x x由图可得:最大值⎪⎩⎪⎨⎧==+35121x x x , 所以⎪⎩⎪⎨⎧==2321x xmax Z = 8.1212125.max 23284164120,1,2maxZ .jZ x x x x x x x j =+⎧+≤⎪≤⎪⎨≤⎪⎪≥=⎩如图所示,在(4,2)这一点达到最大值为26将线性规划模型化成标准形式:Min z=x 1-2x 2+3x 3⎪⎪⎩⎪⎪⎨⎧≥≥-=++-≥+-≤++无约束321321321321,0,052327x x x x x x x x x x x x解:令Z ’=-Z,引进松弛变量x 4≥0,引入剩余变量x 5≥0,并令x 3=x 3’-x 3’’,其中x 3’≥0,x 3’’≥0Max z ’=-x 1+2x 2-3x 3’+3x 3’’⎪⎪⎩⎪⎪⎨⎧≥≥≥≥≥≥-=++-=--+-=+-++0,0,0'',0',0,05232'''7'''5433213215332143321x x x x x x x x x x x x x x x x x x x7将线性规划模型化为标准形式Min Z =x 1+2x 2+3x 3⎪⎪⎩⎪⎪⎨⎧≥≤-=--≥++-≤++无约束,321321321321,00632442392-x x x x x x x x x x x x解:令Z ’ = -z ,引进松弛变量x 4≥0,引进剩余变量x 5≥0,得到一下等价的标准形式。

线性规划建模习题2.某医院昼夜24小时各时间段内需要的护士数量如下:2:00~6:00 10人;6:00~10:00 15人;10:00~14:00 25人;14:00~18:00 20人;18:00~22:00 18人;22:00~2:00 12人。
护士分别于2:00、6:00、10:00、14:00、18:00、22:00分六批上班,并连续工作8小时。
试确定:(a)该医院至少应设多少名护士,才能满足值班需要;(b)若医院可聘用合同工护士,上班时间同正式工护士。
若正式工护士报酬为10元/小时,合同工护士为15元/小时,问医院聘用正式工和合同工护士各多少人成本最低?3.某人有一笔30万元的资金,在今后三年内有以下投资项目:(1)三年内的每年年初均可投资,每年获利为投资额的20%,其本利可一起用于下一年投资;(2)只允许第一年年初投入,第二年年末可收回,本利合计为投资额的150%,但此类投资限额不超过15万元;(3)于三年内第二年初允许投资,可于第三年末收回,本利合计为投资额的160%,这类投资限额20万元;(4)于三年内的第三年初允许投资,一年收回,可获利40%,投资限额为10万元。
试为该人确定一个使第三年末本利和为最大的投资计划。
8.市场对I、II两种产品的需求量为:产品I在1~4月每月需10000件,5 ~9月每月30000件,10 ~12月每月需100000件;产品II在3 ~9月每月15000件,其他月每月50000件。
某厂生产这两种产品成本为:产品I在1 ~5月内生产每件5元,6 ~12月内生产每件4.5元;产品II 在1 ~5月内生产每件8元,6 ~12月内生产每件7元。
该厂每月生产两种产品能力总和不超过120000件。
产品I容积每件0.2立方米,产品II每件0.4立方米,而该厂仓库容积为15000立方米。
要求:(1)若占用本厂每月每立方米库容需1元,该厂应如何安排生产计划,才能在满足市场需求的前提下,确保生产加库存费用最低?(2)上述问题是否有可行解?(3)若该厂仓库不足时,可从外厂租借,租用外厂仓库时上述费用增加为1.5元,试问在满足市场需求情况下,该厂应如何安排生产,使总的生产加库存费用为最少?15.一个大的造纸公司下设10个造纸厂,供应1000个用户。

作业1.第7题A.AB.BC.CD.D答案:D标准答案:D您的答案:题目分数:1.0此题得分:0.02.第8题下列不满足线性规划问题的典式要求的是()。
A. 线性规划模型必须是标准形B. 基必须是单位矩阵。
C. 基变量可以出现在目标函数中D. 非基变量可以出现在目标函数中。
A.AB.BC.CD.D答案:C标准答案:C您的答案:题目分数:1.0此题得分:0.03.第13题A.AB.BC.CD.D答案:B标准答案:B 您的答案:题目分数:1.0 此题得分:0.04.第14题A.AB.BC.CD.D答案:D标准答案:D 您的答案:题目分数:1.0此题得分:0.05.第15题A.AB.BC.CD.D答案:A标准答案:A 您的答案:题目分数:1.0 此题得分:0.06.第16题A.AB.BC.CD.D答案:B标准答案:B 您的答案:题目分数:1.0 此题得分:0.07.第17题A.AB.BC.CD.D答案:A标准答案:A您的答案:题目分数:1.0此题得分:0.08.第18题若用二阶段法求没有可行解的线性规划问题,则在最后一张单纯表上()。
A. 人工变量的检验数没有正数B. 人工变量的检验数没有负数C. 非基变量中有人工变量D. 基变量中有人工变量A.AB.BC.CD.D答案:D标准答案:D您的答案:题目分数:1.0此题得分:0.09.第19题A.AB.BC.CD.D答案:D标准答案:D您的答案:题目分数:1.0此题得分:0.010.第20题若目标函数求极小值的线性规划问题没有最优解,则在最后一张单纯表上()。
A. 对应非基变量的列上的系数没有正数B. 基变量的取值有负数C. 检验数没有负数D. 检验数为负的非基变量对应的列上的系数没有正数A.AB.BC.CD.D答案:D标准答案:D您的答案:题目分数:1.0此题得分:0.011.第21题A.AB.BC.CD.D答案:D标准答案:D您的答案:题目分数:1.0 此题得分:0.012.第26题A.AB.BC.CD.D答案:B标准答案:B您的答案:题目分数:1.0 此题得分:0.013.第28题A.AB.BC.CD.D答案:A标准答案:A您的答案:题目分数:1.0 此题得分:0.014.第33题A.AB.BC.CD.D答案:D标准答案:D您的答案:题目分数:1.0 此题得分:0.015.第34题A.AB.BC.CD.D答案:D标准答案:D您的答案:题目分数:1.0 此题得分:0.016.第35题A.AB.BC.CD.D答案:D标准答案:D您的答案:题目分数:1.0此题得分:0.017.第36题A.AB.BC.CD.D答案:A标准答案:A您的答案:题目分数:1.0此题得分:0.018.第46题检验有无迂回时,必须对()进行。

第一章线性规划习题1.1(生产计划问题)某企业利用A、B、C三种资源,在计划期内生产甲、乙两种产品,已知生产单位产品资源的消耗、单位产品利润等数据如下表,问如何安排生产计划使企业利润最大?表1—1产品单耗资源甲乙资源限制A B C 12111300kg400kg250kg单位产品利润(元/件)50100解:设x1、x2分别代表甲、乙两种产品的生产数量(件),z表示公司总利润。
依题意,问题可转换成求变量x1、x2的值,使总利润最大,即ma x z=50x1+100x2且称z=50x1+100x2为目标函数。
同时满足甲、乙两种产品所消耗的A、B、C三种资源的数量不能超过它们的限量,即可分别表示为x1 + x2≤3002x1 + x2≤400x2≤250且称上述三式为约束条件。
此外,一般实际问题都要满足非负条件,即x1≥0、x2≥0。
这样有ma x z=50x1+100x2x1 + x2≤3002x1 + x2≤400x2≤250x1、x2≥0习题1.2 靠近某河流有两个化工厂,流经第一化工厂的河流流量为每天500万m 3,在两个工厂之间有一条流量为200万m 3的支流。
两化工厂每天排放某种有害物质的工业污水分别为2万m 3和1.4万m 3。
从第一化工厂排出的工业污水流到第二化工厂以前,有20%可以自然净化。
环保要求河流中工业污水含量不能大于0.2%。
两化工厂处理工业污水的成本分别为1000元/万m 3和800元/万m 3。
现在要问在满足环保要求的条件下,每厂各应处理多少工业污水,使这两个工厂处理工业污水的总费用最小。
解:设x 1、x 2分别代表工厂1和工厂2处理污水的数量(万m 3)。
则问题的目标可描述为min z =1000x 1+800x 2约束条件有第一段河流(工厂1——工厂2之间)环保要求 (2-x 1)/500 ≤0.2%第二段河流(工厂2以下河段)环保要求[0.8(2-x 1) +(1.4-x 2)]/700≤0.2%此外有x 1≤2; x 2≤1.4化简得到min z =1000x 1+800x 2x 1 ≥10.8x 1 + x 2 ≥1.6x 1 ≤2x 2≤1.4x 1、x 2≥0习题1.3ma x z =50x 1+100x 2x 1 + x 2≤3002x 1 + x 2≤400x 2≤250图1—1x 2x 1、x 2≥0用图解法求解。


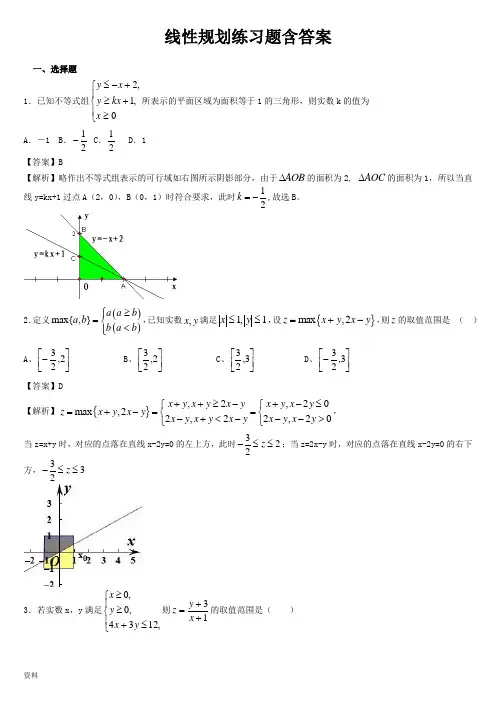
线性规划练习题含答案一、选择题1.已知不等式组2,1,0y x y kx x ≤-+⎧⎪≥+⎨⎪≥⎩所表示的平面区域为面积等于1的三角形,则实数k 的值为A .-1 BD .1 【答案】B【解析】略作出不等式组表示的可行域如右图所示阴影部分,由于AOB ∆的面积为2, AOC ∆的面积为1,所以当直线y=kx+1过点A (2,0),B (0,1故选B 。
2.定义()()max{,}a a b a b b a b ≥⎧⎪=⎨<⎪⎩,已知实数y x ,满足设{}m a x ,2z x y x y=+-,则z 的取值范围是 ( ) A【答案】D【解析】{},2,20max ,22,22,20x y x y x y x y x y z x y x y x y x y x y x y x y ++≥-+-≤⎧⎧=+-==⎨⎨-+<--->⎩⎩, 当z=x+y 时,对应的点落在直线x-2y=0z=2x-y 时,对应的点落在直线x-2y=0的右下3.若实数x ,y 满足⎪⎩⎪⎨⎧≤+≥≥,1234,0,0y x y x 则 )A .BCD【答案】DP(x,y)与点(-1,-3)连续的斜率,数形结3,,4PA k =应选D4.设,x y ∈R 且满足1230x x y y x ≥⎧⎪-+≥⎨⎪≥⎩,则2z x y =+的最小值等于 ( )A. 2B. 3C.5D. 9【答案】B【解析】解:因为设,x y ∈R 且满足满足1230x x y y x ≥⎧⎪-+≥⎨⎪≥⎩故其可行域为当直线Z=x+2y 过点(1,1)时,z=x+2y 取最小值3, 故选B5.若实数,满足条件则的最大值为( )(A ) (B ) (C ) (D ) 【答案】A【解析】作出如右图所示的可行域,当直线z=2x-y 过点A 时,Z 取得最大值.因为A(3,-3),所以Z max =23(3)9⨯--=,故选A.x y 0,30,03,x y x y x +≥⎧⎪-+≥⎨⎪≤≤⎩2x y -9303-6.设变量x ,y 满足约束条件⎪⎩⎪⎨⎧≥+≤+≥-120y x a y x y x ,若目标函数z=2x+6y 的最小值为2,则a =A .1B .2C .3D .4 【答案】A【解析】解:由已知条件可以得到可行域,,要是目标函数的最小值为2,则需要满足直线过x 2y 1+=与x+y=a 的交点时取得。

高考数学一轮复习《线性规划》复习练习题(含答案)一、单选题1.若x ,y 满足1010330x y x y x y +-⎧⎪--⎨⎪-+⎩,则4z x y =-的最小值为( )A .-6B .-5C .-4D .12.已知x ,y 满足不等式组240,3260,20,x y x y x y --≤⎧⎪--≤⎨⎪++≥⎩则23z x y =+的取值范围为( )A .32,5⎡⎫-+∞⎪⎢⎣⎭B .325,52⎡⎤--⎢⎥⎣⎦C .[)6,-+∞D .5,2⎡⎫-+∞⎪⎢⎣⎭3.设变量,x y 满足约束条件100240x y x y x y --≤⎧⎪+≥⎨⎪+-≥⎩,则2z x y =-的最大值为( )A .0B .32C .3D .44.已知实数,x y 满足2030330x y x y x y -+≥⎧⎪+-≤⎨⎪--≥⎩,则目标函数2z x y =+的最大值为( )A .112B .5C .52D .35.若实数x ,y 满足约束条件110x y x y x +≥⎧⎪-≤⎨⎪≥⎩,则2z x y =+的最小值是( )A .-1B .0C .1D .26.若,x y 满足约束条件310x y x y x +≤⎧⎪-≤-⎨⎪≥⎩,则2z x y =+的最小值为( )A .1B .2C .3D .47.不等式44x y +<表示的区域在直线440x y +-=的( ) A .左上方B .左下方C .右上方D .右下方8.已知实数x ,y 满足210,10,2,x y x y x -+≥⎧⎪+-≥⎨⎪<⎩,则z =2x -y 的最小值是( )A .5B .52C .0D .-19.若实数x ,y 满足约束条件23023020x y x y x ++≥⎧⎪--≤⎨⎪+≥⎩,则3z x y =-的最大值是( )A .6-B .2C .4D .610.已知动点(),P m n 在不等式组400x y x y y +≤⎧⎪-≥⎨⎪≥⎩ 表示的平面区域内部及其边界上运动,则35n z m -=-的最小值( ) A .4 B .13C .53D .311.甲、乙两艘轮船都要在某个泊位停靠6个小时,假定它们在一昼夜的时间中随机到达,若两船有一艘在停泊位时,另一艘船就必须等待,则这两艘轮船停靠泊位时都不需要等待的概率为( ) A .1116B .916C .716D .51612.若实数,x y 满足约束条件10210y x y x y ≤⎧⎪-≤⎨⎪++≥⎩,则z )A .1BCD二、填空题13.已知x ,y 满足约束条件1000x y x y y +-≤⎧⎪-≥⎨⎪≥⎩则2z x y =-的最大值为_________.14.已知x 、y 满足2025020x y x y y --≤⎧⎪+-≥⎨⎪-≤⎩,则21x y z x ++=+的最小值是__________.15.在等差数列{}n a 中,125024a a a ≤≥-≤,,,则4a 的取值范围是______. 16.若实数,x y 满足约束条件102310y x x x y ≥⎧⎪+≥⎨⎪+-≤⎩,则目标函数3z x y =+的取值范围是__________ .三、解答题17.制定投资计划时,不仅要考虑可能获得的盈利,而且要考虑可能出现的亏损.某投资人打算投资甲、乙两个项目,根据预测,甲、乙两个项目可能的最大盈利率分别为100%和50%,可能的最大亏损率分别为30%和10%,投资人计划投资金额不超过10万元,要求确保可能的资金亏损不超过1.8万元.(1)设投资人用x 万元、y 万元分别投资甲、乙两个项目,列出满足题意的不等关系式,并画出不等式组确定的平面区域图形;(2)求投资人对甲、乙两个项目各投资多少万元,才能使可能的盈利最大?18.若变量x ,y 满足约束条件240101x y x y x +-≤⎧⎪--≤⎨⎪≥⎩(1)画出不等式组表示的平面区域; (2)求目标函数z =y +x 的最大值和最小值.19.已知点(),P x y 在圆()2211x y +-=上运动,(1)求12y x --的取值范围; (2)求2x +y 的取值范围.20.已知圆C :222440x y x y +-+-=,直线l :30mx y m -+-=()m R ∈与圆C 相交于A 、B 两点.(1)已知点(,)x y 在圆C 上,求34x y +的取值范围: (2)若O 为坐标原点,且2AB OC =,求实数m 的值.21.已知命题p :0x ∃∈R ,()()2011(0)m x a a ++≤>,命题q :x ∀,y 满足+1002x y x y -≤⎧⎪≥⎨⎪≤⎩,m .(1)若q 为真命题,求m 的取值范围.(2)判断p ⌝是q 的必要非充分条件,求a 的范围22.2021年6月17日9时22分,我国“神舟十二号”载人飞船发射升空,展开为期三个月的空间站研究工作,某研究所计划利用“神舟十二号”飞船进行新产品搭载试验,计划搭载若干件新产品,A B 、要根据产品的研制成本、产品重量、搭载试验费用和预计收益来决定具体安排,通过调查,搭载每件产品有关数据如表:(1)试用搭载,A B 产品的件数,x y 表示收益z (万元);(2)怎样分配,A B 产品的件数才能使本次搭载实验的利润最大,最大利润是多少?23.设函数(),()x f x e g x ax b ==+,其中, a b R ∈.(Ⅰ)若1,1a b ==-,当1x ≥时,求证:()()ln f x g x x ≥;(Ⅱ)若不等式()()f x g x ≥在[1,)+∞上恒成立,求()2223a e b -+的最小值.24.对于函数()f x 和()g x ,设集合(){}0,R A x f x x ==∈,(){}0,R B x g x x ==∈,若存在1x A ∈,2x B ∈,使得12(0)x x k k -≤≥,则称函数()f x 与()g x “具有性质()M k ”.(1)判断函数()sin f x x =与()cos g x x =是否“具有性质1()2M ”,并说明理由;(2)若函数1()22x f x x -=+-与2()(2)24g x x m x m =+--+“具有性质(2)M ”,求实数m 的最大值和最小值;(3)设0a >且1a ≠,1b >,若函数1()log x bf x a x=-+与()log x b g x a x=-+“具有性质(1)M ”,求1212x x -的取值范围。


第一章习题1.设用原料A 生产甲、乙、丙的数量分别为131211,,x x x ,用原料B 生产甲、乙、丙的数量分别为232221,,x x x ,原料C 生产甲、乙、丙的数量分别为333231,,x x x ,则可以建立线性规划问题的数学模型:⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎨⎧=≥≤+--≤+--≥--≤+--≥--≤++≤++≤++++++++-+=)3,2,1,(,005.05.05.004.06.06.0015.015.085.008.02.02.006.06.04.0120025002000..8.38.56.78.18.36.52.08.16.3max 332313322212322212312111312111333231232221131211333231232221131211j i x x x x x x x x x x x x x x x x x x x x x x x x x t s x x x x x x x x x S ijLINGO 求解程序见程序max =3.6*x11+5.6*x21+7.6*x31+1.8*x12+3.8*x22+5.8*x32-0.2*x13+1.8*x23+3.8*x33;-0.4*x11+0.6*x21+0.6*x31<0;0.2*x11+0.2*x21-0.8*x31>0;-0.85*x12+0.15*x22+0.15*x32<0;0.6*x12+0.6*x22-0.4*x32>0;0.5*x13+0.5*x23-0.5*x33>0;x11+x12+x13<=2000;x21+x22+x23<=2500;x31+x32+x33<=1200;求解结果:1200,22.1482,33.473,0,78.1017,66.1526322212312111======x x x x x x 0,0,0332313===x x x ,24640max =S (元)。