二、菲涅耳公式表示反射波、折射波与入射波的振幅和位相关

菲涅耳公式电磁波通过不同介质的分界面时发生全反射和折射．这一关系可由菲涅耳公式表达出来．上节提到的在反射过程中发生的半波损失问题，就可以用这个公式来解释．这一公式对以后讲到的许多光学现象都能圆满地加以说明。

中文名菲涅耳公式外文名Fresnel formula概述电磁波通过不同介质的公式内容引言在任何时刻，我们都可公式关系反射、折射瞬间的电矢量目录1介绍2公式内容3公式关系4注意事项5结论6详细分析7实验过程8实验总结1介绍菲涅耳公式是阐述平面电磁波在两种媒质分界面上传播特性的一组公式。

也就是表达反射系数r、折射系数t与媒质1的波阻抗η1、媒质2的波阻抗η2、入射角θi、折射角θt之间内在联系的公式。

常用来计算反射波电场强度06和折射波电场强度Er。

菲涅耳公式共有两套，分别适用于垂直极化平面波和平行极化平面波。

反射系数r反射波电场强度Er与入射被电场强度Ei之比，即r=E r/E i反射系数一般为复数。

折射系数t折射波电场强度与入射波电场强度之比，即t=E r/E i折射系数一般为复数。

垂直极化遗与平行极化波入射线与介质1、2界面的法线所构成的面叫入射面。

入射波电场强度Ei与入射面垂直，称之为垂直极化平面波，简称为垂直极化波；若Ei与入射面平行（或入射波磁场强度Ei与入射面正交），则叫做平行极化平面波，简称为平行极化波。

极化方向任意的入射波，可以看成是由垂直极化波和平行极化波叠加而成的。

斜入射使用的菲涅耳公式垂直投射时的菲涅耳公式当θi=θr=θt=0时，垂直极化波和平行极化波均用下式计算：功率反射系数R与功率折射系数T：每一单位面积的平均反射功率与同一面积内的平均入射功率之比，称为功率反射系数，记作R。

每一单位面积内的平均折射功率与同一面积内的平均入射功率之比，称为功率折射系数。

符号为T。

不论是垂直极化波还是平行极化波，功率反射系数与功率折射系数之和恒等于1，这是能量守恒的必然结果。

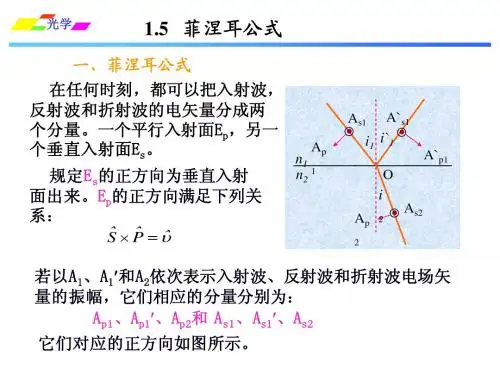
2公式内容引言：在任何时刻，我们都可以把入射波、反射波和折射波的电矢量分成两个分量,一个平行于入射面,另一个垂直于入射面．有关各量的平行分量与垂直分量依次用指标p和s来表示．以i1、i1′和i2分别表示入射角、反射角和折射角,它们确定了各波的传播方向(在大多数情况下,只要注意各波的电场矢量即可,因为知道了各个波的传播方向,各波的磁场矢量就可按右螺旋关系确定)．以A1、A1′和A2来依次表示入射波、反射波和折射波的电矢量的振幅，它们的分量相应就是Ap1、Ap1′、Ap2和As1、As1′、As2．由于三个波的传播方向各不相同,必须分别规定各分量的某一个方向作为正方向，这种规定当然是任意的．但是只要在一个问题的全部讨论过程中始终采取同一种正方向的选择，由此得到的各个关系式就具有普遍的意义．图中xy平面为两介质的分界面,z轴为法线方向，xz平面为入射面．规定电矢量的s分量以沿着+y方向的为正，这对于入射、反射和折射三个波都相同．图中I、II、III三个面依次表示入射、反射和折射三个波的波面．电矢量的p分量沿着这三个波面与入射面的交线,它们的正方向分别规定为如图所示。

Chapter 1 理论基础1.1 介质中的Maxwell ’s equations 及物质方程微分形式=t =J+t ==0B E D H D B ρ⎧∂∇⨯-⎪∂⎪⎪∂∇⨯⎨∂⎪⎪∇⎪∇⎩ （1-1）传导电流密度J 的单位为安培/米2(A/m 2)，自由电荷密度ρ的单位为库仑/米2(C/m 2)。

同时有电磁场对材料介质作用的关系式，即物质方程（或称本构方程）00==()J=D E E PB H H M E εεμμσ⎧=+⎪⎪=+⎨⎪⎪⎩ （1-2）麦克斯韦方程组及物质方程描写了整个电磁场空间及全时间过程中电磁场的分布及变化情况。

因此，所有关于电磁波的产生及传播问题，均可归结到在给定的初始条件和边界条件下求解麦克斯韦方程组的问题，这也正是用以解决光波在各种介质、各种边界条件下传播问题的关键及核心。

1.2 积分形式及边界条件由于两介质分界面上在某些情况下场矢量E 、D 、B 、H 发生跃变，因此这些量的导数往往不连续。

这时不能在界面上直接应用微分形式的Maxwell ’s equations ，而必须由其积分形式出发导出界面上的边界条件。

积分形式0L S L S S S d E dl B d S dt d H dl I D d S dt D d S Q B d S ⎧=-⎪⎪⎪=+⎪⎨⎪=⎪⎪=⎪⎩⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰ （1-3）得边界条件为21212121()0()()()0n E E n H H n D D n B B ασ⎧⨯-=⎪⨯-=⎪⎨⋅-=⎪⎪⋅-=⎩ （1-4）式（1-4）的具体解释依次如下（具体过程详见《光学电磁理论》P20）： （1）电场强度矢量E 的切向分量连续，n 为界面的法向分量。

（2）α为界面上的面传导电流的线密度。

当界面上无传导电流时，α=0，此时H 的切向分量连续。

比如在绝缘介质表面无自由电荷和传导电流。

（3）σ为界面上的自由电荷面密度。

（4）磁感应强度矢量B 的法向分量在界面上连续。

Chapter 1 理论基础1.1 介质中的Maxwell ’s equations 及物质方程微分形式=t =J+t ==0B E D H D B ρ⎧∂∇⨯-⎪∂⎪⎪∂∇⨯⎨∂⎪⎪∇⎪∇⎩ （1-1）传导电流密度J 的单位为安培/米2(A/m 2)，自由电荷密度ρ的单位为库仑/米2(C/m 2)。

同时有电磁场对材料介质作用的关系式，即物质方程（或称本构方程）00==()J=D E E PB H H M E εεμμσ⎧=+⎪⎪=+⎨⎪⎪⎩ （1-2）麦克斯韦方程组及物质方程描写了整个电磁场空间及全时间过程中电磁场的分布及变化情况。

因此，所有关于电磁波的产生及传播问题，均可归结到在给定的初始条件和边界条件下求解麦克斯韦方程组的问题，这也正是用以解决光波在各种介质、各种边界条件下传播问题的关键及核心。

1.2 积分形式及边界条件由于两介质分界面上在某些情况下场矢量E 、D 、B 、H 发生跃变，因此这些量的导数往往不连续。

这时不能在界面上直接应用微分形式的Maxwell ’s equations ，而必须由其积分形式出发导出界面上的边界条件。

积分形式0L S L S S S d E dl B d S dt d H dl I D d S dt D d S Q B d S ⎧=-⎪⎪⎪=+⎪⎨⎪=⎪⎪=⎪⎩⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰ （1-3）得边界条件为21212121()0()()()0n E E n H H n D D n B B ασ⎧⨯-=⎪⨯-=⎪⎨⋅-=⎪⎪⋅-=⎩ （1-4）式（1-4）的具体解释依次如下（具体过程详见《光学电磁理论》P20）： （1）电场强度矢量E 的切向分量连续，n 为界面的法向分量。

（2）α为界面上的面传导电流的线密度。

当界面上无传导电流时，α=0，此时H 的切向分量连续。

比如在绝缘介质表面无自由电荷和传导电流。

（3）σ为界面上的自由电荷面密度。

（4）磁感应强度矢量B 的法向分量在界面上连续。

江西师范大学本科毕业论文题目：菲涅耳公式及其应用Title: Fresnel formula and its application院系名称：物理与通信电子学院专业：物理学类摘要本文主要论述菲涅耳公式及其应用。

我们理论推导菲涅耳公式的表达式，分析入射波、反射波和折射波的相位关系。

文中还进一步探讨菲涅耳公式的应用，详细阐述半波损失、全反射、布儒斯特定律及其相关应用。

关键词：菲涅耳公式，半波损失，全反射，布儒斯特定律AbstractThis paper mainly discusses the Fresnel formula and its application. We deduce the expression of Fresnel formula and analyze the phases of incident wave, reflected wave and refractive wave. In this paper, the applications of Fresnel formula are discussed in detail, including half-wave loss, total internal reflection, Brewster law and corresponding applications.Keywords: Fresnel formula, half-wave loss, total internal reflection, Brewster law目录摘要 (I)Abstract......................................................................................................................... I I 绪论.. (1)1 Huygens的光论 (2)2 光的电磁理论 (2)2．1 磁场的环量和旋度 (2)2．2 磁场的通量和散度 (3)2．3 电磁感应定律 (3)2．4 位移电流 (4)2．5 Maxwell方程组 (4)3 Fresnel公式的导出 (6)3．1 平行分量之间的关系 (7)3．2 垂直分量之间的关系 (8)3．3 适用条件 (10)4 反射光和折射光相对入射光的相位变化 (10)4．1 反射光相对于入射光的位相变化 (10)4．2 折射光相对于入射光的位相变化 (12)5 Fresnel公式的应用 (12)5．1 半波损失 (12)5．2 全反射现象和尼科尔棱镜 (13)5．2．1 全反射 (13)5．2．2 尼科尔棱镜 (14)5．3 Brewster角和用玻璃堆获取线偏振光 (15)5．3．1反射光的偏振状态 (15)5．3．2 Brewster角 (16)5．3．3 透射光的偏振状态 (16)5. 3. 4 用玻璃堆获得线偏振光 (18)6 总结 (19)参考文献 (20)绪论光是人们获取信息的主要媒介。

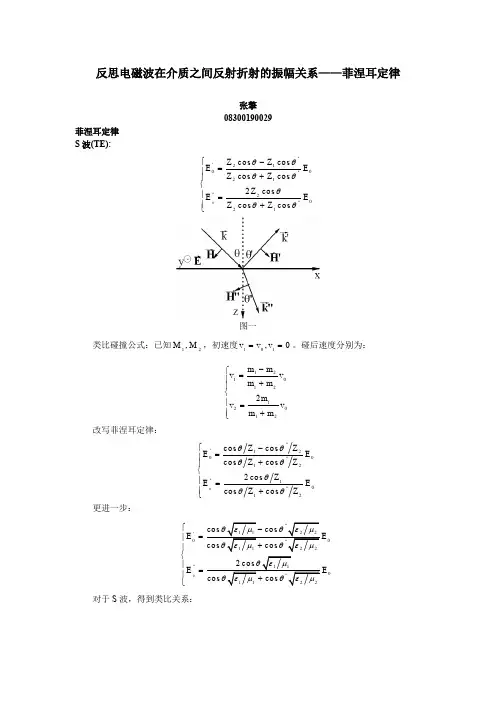
反思电磁波在介质之间反射折射的振幅关系——菲涅耳定律张擎 0830*******菲涅耳定律 S 波(TE):'''2100''21''20''21cos cos cos cos 2cos cos cos Z Z E E Z Z Z E E Z Z θθθθθθθ⎧-=⎪+⎪⎨⎪=⎪+⎩图一类比碰撞公式：已知12,M M ，初速度101,0v v v ==。

碰后速度分别为：121012120122m m v v m m m v v m m -⎧=⎪+⎪⎨⎪=⎪+⎩改写菲涅耳定律：'''1200''12''1''12cos cos cos cos 2cos cos cos Z Z E E Z Z Z E E Z Z θθθθθθθ⎧-=⎪+⎪⎨⎪=⎪+⎩ 更进一步：0'00''0E E E ⎧=⎪⎪⎨⎪=⎪⎩对于S 波，得到类比关系：cos M vEθ→⨯→特别的，当正入射时：M vE→→P 波(TM):'''1200''12''10''12cos cos cos cos 2cos cos cos Z Z H H Z Z Z H H Z Z θθθθθθθ⎧-=⎪+⎪⎨⎪=⎪+⎩图二同样的，改写菲涅耳定律：0'00''0H H H H ⎧=⎪⎪⎨⎪=⎪⎩对于P 波，得到类比关系：cos M vHθ→⨯→特别的，当正入射时：M vH→→讨论：1、 电场（磁场）的反射、折射现象的振幅，可以看成由电场（磁场）驱动原子振动，当在同一介质中时，可以认为电磁波在每个原子上反复被吸收又被辐射出来，由于同一介质的原子的性质相同（反映在电动力学中为介电常数ε和磁导率μ相同），所以，就如同相同质量的完全弹性碰撞一样（12M M =，初速度101,0v v v ==；末速度1100,v v v ==），做无反射的传播。