当前位置：文档之家 › 第四章 频功率放大器

第四章 频功率放大器

  • 格式：doc
  • 大小：221.00 KB
  • 文档页数：7

下载文档原格式

  / 7

合集下载

chap4高频功放

chap4高频功放
式中
1 1 sin cos I co iC d ( t ) iC max ( ) 2 1 cos a0 ( )iC max I c1 1

1



iC cos td ( t )
iC max sin cos 1 cos
uBE
动态线方程式
U CC uCE U BB U bm UCE iC Gc (U BB U bm U on ) U cm
(4-8)
令 uCE=UCC 时， iC=Gc(UBB-Uon) 为图 4-5 中的 Q 点；再令 U Uon 为图4-5中的B点。 iC=0时， u U BB U
(4-4)
集电极直流电源供给功率PDC等于集电极电流直流 分量与UCC的乘积
PDC UCC I c 0
(4-5)
放大器集电极效率等于输出功率与直流电源供给 功率之比，即
Po 1 U cm I c1 1 a1 ( ) 1 c g1 ( ) PDC 2 UCC I co 2 a0 ( ) 2
＋22.5 V
3DA21C V
Cb
L1
L2
C1
C2
图 4-13一超短波输出放大器的实际电路
2． 耦合回路 图4-14是一短波发射机的输出放大器， 它采用互 感耦合回路作输出电路， 多波段工作。
M Cb C1 K
V1
L3
C2 L1 L2
－24 V
图4-14 短波输出放大器的实际线路
R1
R2
(a)
(b)
(c)
图 4-11几种常见的LC匹配 (a) L型；(b) T型； (c) Π型

第4章高频谐振功率放大器

第4章高频谐振功率放大器
若保持Po不变，将ηC提高到80％ ，则
Pc′= PE′Po=Po/ηC′－Po=4/0.8－4=5－4=1W △ Pc =Pc － Pc′= 3.67－1=2.67W △Ic0 = Ic0 －Ic0′= 6.67/20 －5/20 = 0.083（A）=83mA
4.2.3 工作状态分析
一、动态特性分析：
其中0(θ)、1(θ) 、…、n (θ)为谐波分解系数；另 定义1=Ic1m/Ic0= 1(θ) / 0(θ)为波形系数，随减小 而增大。
0 , 1 , 2 , 3
1 /0 = 1
0.5
1
0.4
0
2.0
0.3
0.2
1.0
0.1
3
2
0
-0.05 10 30 50 70 90 110 130 150 170
目的：能够使电信号能够有效地进行远距离传输 特点：高频、大信号、非线性工作 要求：输出功率大、转换效率高
分析方法：折线法近似分析
联想对比：
高频功率放大器和低频功率放大器的共同 特点都是输出功率大和效率高。
功率放大器实质上是一个能量转换器，把电源 供给的直流能量转化为交流能量，能量转换的能力 即为功率放大器的效率。
临界饱和线斜
如图，对应于临界状态的 动特性曲线CAD，则有
率记为：SC
ic C UBE=UBB+Uim
iC max ScuCE min Sc (UCC Uc1m )
根据转移特性，又有
A UCC D
uCE
0
B
UBE=UBB
iC max gm (uBE max U D ) gm (U BB U im U D )
谐振功率放大器与小信号谐振放大器的异同之处

第4章高频功率放大器

第4章高频功率放大器
2、作出动态特性曲线
3、是根据激励电压vb的大小在已知理想特性曲线上画出对 应电流脉冲ic和输出电压vc的波形
4、求出ic的各次谐波分量Ic0、Ic1、Ic2……由给定的负载谐 振阻抗的大小，即可求得放大器的输出电压、输出功率、 直流供给功率、效率等指标
二、晶体管特性曲线的理想化及其特性曲线
根据理想化原理晶体管的静态转移特性可用交横轴于VBZ 的一条直线来表示(VBZ为截止偏压)。
ic
ic
Q
o
eb o
t
小信号谐振放大器 波形图
t
o
eb o
t
V BZ
谐振功率放大器 波形图
t
ic
ic
Q
o
eb o
t
小信号谐振放大器 波形图
t
ic
ic
o
eb o
t
VBZ
谐振功率放大器 波形图
t
4、谐振功率放大器与非谐振功率放大器的异同
共同之处:都要求输出功率大和效率高。
功率放大器实质上是一个能量转换器，把电源供给的直 流能量转化为交流能量，能量转换的能力即为功率放大器 的效率。
当t=0时，ic= ic max 因此，ic max= gcVbm(1–cos c)
ic max
o
t
2c
尖顶余弦脉冲
eb= –VBB+Vbmcosc=VBZ
若将尖顶脉冲分解为傅里叶级数
ic =Ic0+Icm1cost+Icm2cos2t+…+Icmncosnt+…
由傅里叶级数的求系数法得
第 4 章 高频功率放大器
4.1 概述 4.2 谐振功率放大器的工作原理 4.3 晶体管谐振功率放大器的折线近似分析法 4.4 晶体管功率放大器的高频特性 4.5 高频功率放大器的电路组成

高频功率放大器

高频功率放大器

返回
上午9时 19分 12 退出
4.2 谐振功率放大器分析
4.2.1 晶体管特性曲线的理想化及其解析式 4.2.2 集电极余弦电流脉冲的分解 4.2.3 高频功率放大器的工作状态分析
返回
上午9时 19分 13 退出
4.2.1 晶体管特性曲线的理想化及其解析式
在工程上，对于工作频率不是很高的谐振功率放大器 的分析、计算，通常采用准线性的折线分析法。 准线性放大是指仅考察集电级输出电流中的基波分量 在负载两端产生输出电压的放大作用。 折线近似分析法(简称折线法)，这是一种图解法与数 学解析分析相折中的办法，指用几条直线来代替晶体 管的实际特征曲线，然后用简单的数学解析式写出它 们的表示式。缺点是准确度低，但计算比较简单，易 于进行概括性的理论分析。
上午9时 19分
这就是集电极余弦脉冲电流随时间变化的解析式。它取 决于脉冲高度iCmax和半导通角c 。 返回 18 退出
iC I c0 I c1m cosωt I c 2m cos2ωt I cnm cosnt .2.11) (4
直流分量、 基波及各次 谐波的幅值

high
上午9时 19分
丙类(C类)放大器的效率最高，但是波形失真也最 严重。 8 退出
3. 高频功率放大器与小信号谐振放大器
高频小信号谐振放大器与谐振功率放大器的区别： ① 工作状态分别为：小信号-甲类，大信号-丙类。也 就是说，除了输入信号幅度不同外，晶体管的工作点 和晶体管动态范围都不相同。 高频功放常采用效率较高的丙类工作状态，因
在功率放大器中，往往选择静态工作点，使功率管 运用在特性的不同区段上，实现甲类、乙类、甲乙类、 丙类等不同运行状态。 根据正弦波激励下整个周期内的导通情况，可分为 四个工作状态：

功放与扬声器PPT课件

功放与扬声器PPT课件
3、非线性失真：包括总谐波失真和互调失真，专业功放 的总谐波失真要在0.1%以下，互调失真在0.02%以下。
4、噪声与信噪比：噪声指功放输入端不加任何信号时， 作为负载的扬声器所发出的声音（来自内部电路），信 噪比指功放输出的有用信号与噪声之比，专业功放的信
噪比值应大于100dB。
.
6
5、阻尼系数：指扬声器阻抗与功放输出阻抗的比值， 该系数的大小会影响重放音质，通常阻尼系数大，表 明功放的输出内阻很低。
B、晶体管功放：体积小，功率大，耗能低，技术指标 高，具有良好的瞬间特性。
C、集成电路功放：噪声小，动态范围大，无需保护。
.
4
二、功放的性能指标
1、输出功率：是功放送给扬声器的电功率，它包括： A、额定功率：指在不失真的前提下，功放的最大输
出功率。 B、最大输出功率：不考虑失真的大小，将功放音量开
B、主声扬声器：面对观众，辐射全场。 C、补声扬声器：侧后方，弥补主声不足。 D、巡回演出扬声器：大功率，移动方便。 E、影院扬声器：适应数码技术，语言清晰，穿透力强。 5、按外形来分：圆锥形、球顶形、号角形。
.
14
二、扬声器的工作原理（以电动式纸盆扬声器为例）：
1、纸盆扬声器的结构（如图）： 由锥形纸盆、音圈、定心支片组成。纸盆由盆架与定
到最大，此时它所提供的电功率。 C、音乐输出功率：在输出不失真的情况下，功放对音
乐信号的瞬间最大输出功率。 D、峰值音乐输出功率：不考虑失真的大小，功放所能
提供的最大音乐功率。
.
5
2、频率响应：指在指定频带内各频率成分的增益特性， 即不允许产生高（低）频音的增益不平均的情况，高质 量的功放的频率响应在20――20KHz内，不平均度应保 持在（正负）0.5dB以内。

Chapte4高频功率放大器100页PPT

Chapte4高频功率放大器100页PPT

高频功率放大器中各部
(b)
分电压与电流的关系
3、LC回路的能量转换过程
回路是由L、C二个储能元件组成。
回路的这种滤波作用也可从能量的观点来解释。
–+
当晶体管由截止转入导电时，由于回路中
电感L的电流不能突变，因此，输出脉冲电 流的大部分流过电容C，即使C充电。充电电 压的方向是下正上负。这时直流电源VCC给
Pc T 1
T
0iCvCE dt
1. iC 与vBE同相，与vCE反相； 2. iC 脉冲最大时，vCE最小； 3. 导通角和vCEmin越小，Pc越小；
电 流
或 电 压
Vcm
vc
ic
VCE VCC
ic
ic maxvcE min
VBZ
VBE max
t
o c
3

vBE
Vbm vb
–+ C
+–
iL
L
出的能量储存在电容C之中。过了一段时间，
当电容两端的电压增大到一定程度(接近电源
ic + –
电压)，晶体管截止，电容通过电感放电，下
一周期到来重复以上过程。
LC回路能量转换过程
由于这种周期性的能量补充，所以振荡回路能维持振荡。当补 充的能量与消耗的能量相等时，电路中就建立起动态平衡，因而 维持了等幅的正弦波振荡。
4.3 晶体管谐振功率放大器的 折线近似分析法
4.4 晶体管功率放大器的高频特性 4.5 高频功率放大器的电路组成 4.6 晶体管倍频器
4.1 概 述
1、使用谐振功率放大器的目的
放大高频大信号使发射机末级获得足够大的发射功率。
2、功率信号放大器使用中需要解决的两个问题：

课件高频功率放大器ppt

课件高频功率放大器ppt
放大器的基本组成
放大器由输入级、输出级和中间级 组成，其中输入级和输出级是关键 部分，直接影响放大器的性能。
高频放大器的特殊问题
01
02
03
频率响应
高频信号的频率较高，因 此高频放大器的频率响应 需要足够宽，以适应不同 频率的信号放大。
相位失真
由于高频信号的频率较高， 相位失真成为高频放大器 的一个重要问题，需要采 取措施进行补偿。
噪声系数是指放大器输出端的信噪比与输 入端的信噪比之比，是衡量放大器噪声性 能的重要指标。
动态范围是指放大器在保证一定信噪比的 前提下，能够放大的信号的最大幅度范围 ，是衡量放大器适应能力的重要指标。
03 电路分析
晶体管放大电路
01
晶体管放大电路的基本原理
晶体管放大电路利用晶体管的放大效应，将微弱的电信号放大成较强的
利用人工智能和机器学习技术 对高频功率放大器进行智能控 制和优化，提高其自适应能力 和稳定性。
多模多频段技术
研究多模多频段的高频功率放 大器，以满足不同通信标准和
频段的需求。
THANKS FOR WATCHING
感谢您的观看
高频功率放大器用于放大雷达发射的信号，提高雷达对目标的
探测能力。
距离测量
02
通过测量发射信号与接收回波的时间差，高频功率放大器有助
于提高雷达的距离测量精度。
速度测量
03
利用多普勒效应原理，高频功率放大器有助于提高雷达的速度
测量精度。ຫໍສະໝຸດ 音频处理系统中的应用1 2
音频放大
高频功率放大器用于放大音频信号，提供足够的 功率以驱动扬声器或其他音频输出设备。
应用场景
通信领域
高频功率放大器广泛应用于通信领域，如移动通信、卫星通信、光纤 通信等，用于信号的传输和放大。

第四章 高频功率放大器

第四章 高频功率放大器

第四章 高频功率放大器4-1）若非线性特性用折线近似表示，如题图4-1所示，,/10,1V mA g V V bz ==偏压,2V V bb -=激励电压V U 2.5=。

求电流i 的各个分量幅度.,,210I I I 若要加大1I ，应怎样改动U V bb 和？【解】 （1） )c o s(bz bb V wt U V g i -+=当 ,,0Φ==wt i 即 0)cos (=-Φ+bz bb V U V g故552.5)2(1cos cos 11=--=-=Φ--U V V bb bz又 I i wt ==,0故mA I a I mAI a I mA I a I a I mA V V mA V U V g I m m m m bZ bb m 622273.0)55(05.822366.0)55(4.422201.0)55()(22)12.52(/10)(2211000=⨯===⨯===⨯==Φ==-+-∙=-+=（2）因m I a I )(11Φ=要 ,1↑I 应 .,)(1↑↑Φm I a 要使,)(1↑Φa 在 120<Φ时，应增加Φ，即减小b b V；要使,↑m I 应增大U 。

4-2）题图4-2所示为晶体管转移特性，用它作二倍频器，为了使c i 中的二次谐波的成分最大，bb V 应如何选取？（bb V 是直流偏压，设U V bz ,均固定不变）。

【解】 因U V V bbbz -=ϕcos当60=ϕ时，二次谐波分量最大，而,2160cos =故有U V V bbbz -=21，即UV V bz bb 21-= 4-3）某谐振高频功率放大器原理如题图4-3所示，已知信号电压为.cos t w U u s s =假设0f 远小于晶体管的特征频率T f ，负载回路为谐振于0ω的高Q 回路，试画出cc c c b bc u u i i u ,,,,的波形示意图（要求各波形图的时间轴对齐）。

第四章高频功率放大器

第四章高频功率放大器
ηC＝ ＝
P0
P＝
P0
P0＋PC
集电极效率：
可见，提高效率ηc的关键是减小集电极耗散功率Pc。
集电极耗散功率PC的计算式为：
可见，减小Pc的方法有三种： 减小半流通角θc。 在2 θc内，iC最大时，vCE最小。 在2 θc内之外， 虽然vCE最大，但iC＝0。
由谐振功率放大器中各部分电压与电流的波形可知，iC于vCE正好满足上述几个条件。此即丙类谐振功率放大器效率高的原因。
（2）过压状态：集电极最大点电流正好位于临界线左方饱和区。 此时，c较高（弱过压状态最高)；负载阻抗变化时，vCE 基本不变；用于发射机中间级。
（3）欠压状态：集电极最大点电流正好位于临界线右放大区。 Po较小； c较低；PC大；输出电压不稳定；很少采用， 基极调幅电路工作于此状态。
解：1.根据右图可求 根据
，可求得
∴ 晶体管安全工作
4. 求交流电压的振幅
5. 求各功率与效率
∴ 晶体管安全工作
6. 激励（输入）功率
例4. 3 某高频功率放大器工作在临界状态，已知其工作频率f＝520MHz，电源电压VCC=25v，集电极电压利用系数ξ=0.8，输入激励信号电压的幅度Vbm =6v，回路谐振阻抗RP=50Ω，放大器的效率ηC＝75％。求(1) Vcm 、Icm1、输出功率Po、集电极直流能源P＝及集电极功耗PC. (2) 当激励电压Vbm增加时，放大器过渡到何种工作状态？当负载阻抗Rp增 加时，放大器由临界状态过渡到何种工作状态？
§4.1 概述
§4.2 谐振功率放大器的工作原理
由上堂课折线化分析法可知：
由于晶体管基极偏置电压为负值，在输入信号的一个周期内，晶体管的导通时间小于半个周期。因此，工作于丙类工作状态。晶体管的集电极电流是一个脉冲电流串，产生了严重的非线性失真。

第四章高频功率放大器

第四章高频功率放大器

0 120 • n 次谐波取最大值时的流通角为： n

= 60。 • 三次谐波最大值出现在 = 40。
可以看出，基波最大值出现在 = 120处。
1 1 .32 ，这与效率有关。 但是此时 0
因此， 值的选择需综合考虑。

例：如果某个非线性器件的伏安特性可用折线 表示，其中， V B Z =1V，g=10mA/V。现加偏置 电压为VB=-1V，输入余弦信号的幅值Vim=4V， 查表（pp366-368）计算电流中的直流、基波 和二倍频分量幅值。
谐振功率放大器的各 极电压、电流波形
7.2.1
二、输出功率与效率
在谐振功率放大器中，由于其静态工作点选择在集电极电流 为零的情况，因而消除了静态功耗，提高了工作效率。
如何进一步提高效率，则是需要研究的问题。这涉及如何合 理地利用好晶体管转移特性的非线性。 Po Po：输出信号的功率 谐振功放的效率定义为： PD PD：电源提供的功率
三、谐振功率放大器与低频功率放大器的异同点
相同点：1、都要求输出功率大和效率高；2、激励信号幅度均 为大信号。 不同点：1、工作频率与相对频宽不同；2、放大器的负载不同； 3、放大器的工作状态不同。
四、谐振功率放大器与小信号谐振放大器的异同点
相同点：1、放大的信号均为高频信号；2、放 大器的负载均为谐振回路。 不同点：1、激励信号幅度大小不同；2、放大 器的工作点不同；晶体管动态范围不同。
2 1 12 V c m 输出信号功率为 ：P I V I R o c m 1 c m c m 1 2 2 2 R
i () • Icm1: 集电极电流中的基波分量幅度 I cm 1 c max 1
1 P i V o c m ax 1 cm 因此得： 2

高频电子线路最新版课后习题解答第四章 高频功率放大器习题解答

高频电子线路最新版课后习题解答第四章 高频功率放大器习题解答

思考题与习题4.1 按照电流导通角θ来分类，θ=180度的高频功率放大器称为甲类功放，θ>90度的高频功放称为甲乙类功放，θ=90度的高频功率放大器称为乙类功放，θ<90度的高频功放称为丙类功放。

4.2 高频功率放大器一般采用LC谐振回路作为负载，属丙类功率放大器。

其电流导通角θ<90度。

兼顾效率和输出功率，高频功放的最佳导通角θ= 60～70 。

高频功率放大器的两个重要性能指标为电源电压提供的直流功率、交流输出功率。

4.3 高频功率放大器通常工作于丙类状态，因此晶体管为非线性器件，常用图解法进行分析，常用的曲线除晶体管输入特性曲线，还有输出特性曲线和转移特性曲线。

4.4 若高频功率放大器的输入电压为余弦波信号，则功率三极管的集电极、基极、发射极电流均是余弦信号脉冲，放大器输出电压为余弦波信号形式的信号。

4.5 高频功放的动态特性曲线是斜率为1-的一条曲线。

R∑υ对应的静态特性曲线的交点位于放大区就4.6对高频功放而言，如果动态特性曲线和BEmaxυ称为欠压工作状态；交点位于饱和区就称为过压工作状态；动态特性曲线、BEmax 对应的静态特性曲线及临界饱和线交于一点就称为临界工作状态。

V由大到小变化时，4.7在保持其它参数不变的情况下，高频功率放大器的基级电源电压BB功放的工作状态由欠压状态到临界状态到过压状态变化。

高频功放的集电极V（其他参数不变）由小到大变化时，功放的工作状态由过压状态到电源电压CCV（其它参数不变）由小临界状态到欠压状态变化。

高频功放的输入信号幅度bm到大变化，功放的工作状态由欠压状态到临界状态到过压状态变化。

4.8 丙类功放在欠压工作状态相当于一个恒流源；而在过压工作状态相当于一个恒压源。

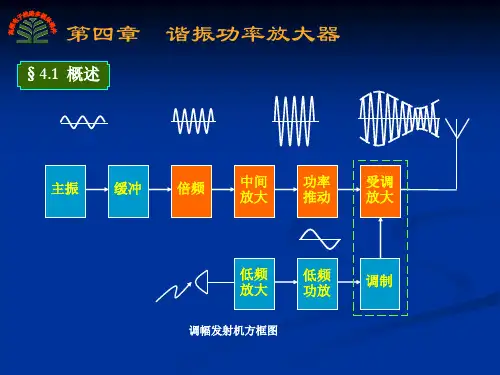
集电极调幅电路的高频功放应工作在过压工作状态，而基级调幅电路的高频功放应工作在欠压工作状态。

发射机末级通常是高频功放，此功放工作在临界工作状态。

4.9 高频功率放大器在过压工作状态时输出功率最大，在弱过压工作状态时效率最高。

低频功率放大器(课件)

低频功率放大器(课件)

L M Ma
电流经C流向RL,同时对电容C进行充电．
27
RC3
VD1 VD2
ui
V3
Re3
(a)
ui
+Vcc
0
t
V1 C
uVe 3
＋
uO
－
RL
V2
0
uO
t
0
t
-VEE
当ui为正半周期时,经V3倒相加在V1 和V2的基极,使V２导通,V１截止.
电流经C流向V2, 电容C充当电源对V2进行放电．
电容C要足够大,使电容的充放时间远大于ui的周期.这样在ui周期 变化的过程中,uc基本不变,从而使负载RL上 获得稳定的交流电.
4.2.2 、甲乙类互补对称功率放大电路
实际电路中，静态电流通常取得很小，所
以这种电路仍可以用乙类互补对称电路的有 关公式近似估算输出功率和效率等指标。
L M Ma
25
甲乙类互补对称功率放大电路如下图:
RC3
VD1 VD2
ui
V3
Re3
(a)
+Vcc V1
RL V2
-VEE
利用二极管进 行偏置的电路
2.
在OCL电路中, 每只三极管集电极静态电流为零, 因而该 电路效率高。
L M Ma
16
1） 输出功率Po
当输入正弦信号时，每只三极管只在半周期内工作，
忽略交越失真，并设三极管饱和压降UCES=0，在Uom≈UCC 时输出电压幅度最大。最大交流输出功率为:
Po
UoIo
Uom 2
Iom 2
UomIom 2
L M Ma
4
3. 非线性失真
功率放大器为了获得足够大的输出功率，需要大 信号激励， 从而使信号动态范围往往超出晶体管的线 性区域，导致输出信号失真。因此减小非线性失真， 成为功率放大器的又一个重要问题。

最新第4章 高频谐振功率放大器PPT课件

最新第4章 高频谐振功率放大器PPT课件

L
分布电容影
Cc
响小；但 LC处于直
UCC
Lc
流高电位上，
网装络不元方件便安。(a) 串联馈电电路
LC处于直流地 电位上，网络元 件安装方便；但 分布参数直接影 响网络的调协。
VT
Lc
Cc2
CL
UCC
(b) 并联馈电电路 Cc1
VT L
C
L
VT
×
Lc
×
UCC
Lc
Cc
Lc
×
VT
Lc
UCC
VT
×
L C
直流通路
丁类功率放大器的晶体管工作于开关状态，管子导通时进入饱和 区，器件内阻接近于0，截止时电流为0，这样可以使集电极功耗大 为减小，效率大大提高，在理想情况下，效率可达100%，实际情况 下也可达90%左右。但由于开关管转换频率越高，损耗越大，故其上 限工作频率受限。
丁类功放分为电流开关型和电压开关型两种电路。
第4章 高频谐振功率放大器
§4.2 丙类高频谐振功率放大器的工作原理
一、基本电路构成及工作原理
组成：BJT、LC谐振回路、馈电电源
特点：
iC
iB
VT uBE uCE
C
L
RL
1、NPN高频大功率晶体管，
ui
高fT；改变UBB可以改变放大器 的工作类型；
UBB
UCC
2、大信号激励：1～2V；
3、发射结在一个周期内只有部分时间导通，iB、iC均为一系列高频脉冲；
RL上基波电压振幅：
ULm 2(UCC 2Uce)s
基波电流振幅：
ILm
ULm RL
输出功率：
P0
1 2

功率放大器原理[定稿]

功率放大器原理[定稿]

功率放大器原理[定稿]第一篇：功率放大器原理[定稿]一、功率放大器简介利用三极管的电流控制作用或场效应管的电压控制作用将电源的功率转换为按照输入信号变化的电流。

因为声音是不同振幅和不同频率的波，即交流信号电流，三极管的集电极电流永远是基极电流的β倍，β是三极管的交流放大倍数，应用这一点，若将小信号注入基极，则集电极流过的电流会等于基极电流的β倍，然后将这个信号用隔直电容隔离出来，就得到了电流(或电压)是原先的β倍的大信号，这现象成为三极管的放大作用。

经过不断的电流及电压放大，就完成了功率放大。

编辑本段二、功率放大器种类传统的数字语音回放系统包含两个主要过程：（1）数字语音数据到模拟语音信号的变换(利用高精度数模转换器DAC)实现；（2）利用模拟功率放大器进行模拟信号放大，如A类、B类和AB 类放大器。

从1980年代早期，许多研究者致力于开发不同类型的数字放大器，这种放大器直接从数字语音数据实现功率放大而不需要进行模拟转换，这样的放大器通常称作数字功率放大器或者D类放大器。

1、A类放大器A类放大器的主要特点是：放大器的工作点Q设定在负载线的中点附近,晶体管在输入信号的整个周期内均导通。

放大器可单管工作，也可以推挽工作。

由于放大器工作在特性曲线的线性范围内，所以瞬态失真和交替失真较小。

电路简单，调试方便。

但效率较低，晶体管功耗大，功率的理论最大值仅有25％，且有较大的非线性失真。

由于效率比较低现在设计基本上不在再使用。

2、B类放大器B类放大器的主要特点是：放大器的静态点在(VCC，0)处，当没有信号输入时，输出端几乎不消耗功率。

在Vi的正半周期内，Q1导通Q2截止，输出端正半周正弦波；同理，当Vi为负半波正弦波(如图虚线部分所示)，所以必须用两管推挽工作。

其特点是效率较高(78%)，但是因放大器有一段工作在非线性区域内，故其缺点是“交越失真”较大。

即当信号在-0.6V~ 0.6V之间时，Q1 Q2都无法导通而引起的。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第四章 高频功率放大器4-1）若非线性特性用折线近似表示，如题图4-1所示，,/10,1V mA g V V bz ==偏压,2V V bb -=激励电压V U 2.5=。

求电流i 的各个分量幅度.,,210I I I 若要加大1I ，应怎样改动U V bb 和？【解】 （1） )cos (bz bb V wt U V g i -+=当 ,,0Φ==wt i 即 0)cos (=-Φ+bz bb V U V g故ο552.5)2(1cos cos 11=--=-=Φ--U V V bb bz又 I i wt ==,0故mA I a I mAI a I mA I a I a I mA V V mA V U V g I m m m m bZ bb m 622273.0)55(05.822366.0)55(4.422201.0)55()(22)12.52(/10)(2211000=⨯===⨯===⨯==Φ==-+-•=-+=οοο（2）因m I a I )(11Φ=要 ,1↑I 应 .,)(1↑↑Φm I a 要使,)(1↑Φa 在ο120<Φ时，应增加Φ，即减小b b V；要使,↑m I 应增大U 。

4-2）题图4-2所示为晶体管转移特性，用它作二倍频器，为了使c i 中的二次谐波的成分最大，bb V 应如何选取？（bb V 是直流偏压，设U V bz ,均固定不变）。

【解】 因U V V bbbz -=ϕcos当ο60=ϕ时，二次谐波分量最大，而,2160cos =ο故有U V V bbbz -=21，即UV V bz bb 21-= 4-3）某谐振高频功率放大器原理如题图4-3所示，已知信号电压为.cos t w U u s s ο=假设0f 远小于晶体管的特征频率T f ，负载回路为谐振于0ω的高Q 回路，试画出cc c c b bc u u i i u ,,,,的波形示意图（要求各波形图的时间轴对齐）。

【解】4-4）在上题中将负载回路改为谐振于 02ω的高Q 回路，试画出.,,,.ce c c be u u i u 的波形示意图。

【解】4-5）已知谐振功率放大器的输出功率W P 5~=，集电极电源电压为V V ce 24+=试问： （1）当集电极效率为%60=c η时，计算集电极耗散功率,c P 电源供给功率0P 和集电极电流的直流分量co I 。

（2）若保持输出功率不变，而效率提高为80%，问集电极耗散功率c p 减少了多少？【解】 （1）因 c c P P P +=~~η所以，~1P P ccc •-=ηη将数据代入W P c 33.356.06.01=⨯-=W P P P c 33.8533.3~0=+=+=AV P I cc co 347.02433.80===(2) 若%80=c η 则W P c 25.158.08.01'=⨯-=cP 的减少量W P P P c c c 08.225.133.3'=-=-=∆ 按百分比计算: c P 减少了%62%10033.308.2=•4-6) 设谐振高频功率放大器的集电极电流通角ϕ分别为180度,90度,和60度,在上述三种情况,放大器均工作于临界状态,它们的cm cc I V ,也均相同,是分别画出它们理想化动态特性曲线,并计算三种通角情况下集电极效率η的比值,输出功率~P 的比值.【解】说明: 因cmI 均为临界状态,所以,可由,cm I 值在临界线上确定出点A.因cc V 均相同,所以过cc V 点做横轴的垂线MN ，三种情况的工作点均应在此MN 上,(1) 现考虑刚刚为ο180=ϕ状态(全流通)，则其静态工作点的电流应为cm I 21,由cmI 21在MN 上得Q 点,连接AQ 并延长到与横轴相交于D ，则直线AD 即为ο180=ϕ时的动态特性曲线.注：也可由A 点做横轴垂线得m in ce u 再在横轴上取min 2ce cc u V -得D 点,连接AD 即为ο180=φ时的动态特性曲线.(2) 对于ο90=φ状态,直接在横轴上取cc V 点,即为其静态工作点'Q .连接.,''D Q AQ 则折线D AQ '即为ο90=φ时的动态特性曲线..(3).对于ο60=φ状态,因5.060cos cos ==οφ.所以可在MN 线上自cc V 点向下取cm I 即得''Q ,连线''AQ 与横轴相交于B,则折线ABQ,即位ο60=φ时的动态特性曲线；注：也可以由m in ce u 和cc V 的中点得到B 点。

计算：?:?:?)60(:)90(:)180(=οοοηηη因cc ccm cm cc c cc c V U a I a I V U I I ••••=•=)()(2121011ϕϕη 因三种情况下的c cc U V ,均相同所以，)60(:)90(:)180(οοοηηη8.1:57.1:1)60()60(:)90()90(:)180()180(0010101==a a a a a a οοοοο计算：?:?:?)60(:)90(:)180(~~~=οοοP P P因c cm c c U a I U I P ••==)(212111~ϕ因三种情况下c cm U I ,均相同 所以，)60(:)90(:)180(~~~οοοP P P782.0:1:1591.0:5.0:5.0)60(:)90(:)180(111===οοοa a a4-7）要求高频放大器的输出功率.8.1~W P =现选用高频AD12)20,5(W P A I CM CM ==临界饱和线斜率./6.0V A g cr =选定V V cc 18=，通角ο90=ϕ，工作于临界状态。

试计算：电源供给的直流功率οP ，集电极耗散的功率,c P 集电极效率η及满足输出功率要求的等效负载谐振阻抗pR 。

【解】先求01,c c I I :因11~21c c U I P =故1~1~122a I P I P U cm c c == 而crcm cc cr c cc cm g a I P V g U V I )2()(1~1•-=•-=故02~121=+••-cr cm cr cc cm g P I a g V I a 1~1211224)(a g P a a g V a g V I cr cr cc cr cc cm⨯-±••=A A 38.1042.02{5.026.08.125.04)5.06.018(5.06.018=⨯⨯⨯⨯⨯-⨯⨯±⨯⨯ 因A I cm 38.10=超过3AD12的极限量，故舍去取A I cm 42.0=故A a I I ocm c 21.05.042.0)90(11=⨯=•= Ω=⨯======-=-==⨯=•==⨯=•=6.81)21.0(8.122%7541.2/8.1/61.08.141.241.2134.018134.0319.042.0)90(221~0~~00000c p c c cc o cm c I P R P P WP P P W I V P A a I I η4-8）试画出一级具有下列特点的高频谐振功率放大器的实用电路图：（1）采用了高频功率管3DA14B,它的集电极与管壳相连，为便于散热此集电极与相架相连接。

（2）负载为天线（等效参数为A r ，A c ）。

输出回路采用串联谐振型匹配网络。

（3）输入端采用T 型匹配网络。

（4）集电极直流馈电采用串联形式，基极采用零偏置电路。

（5）对高频信号而言应为共射极电放大器。

【解】按上述要求电路图如下：说明：（1）按题意集电极电极应接地。

又要求对高频信号而言为共发电路，所以输入信号应加个高频变压器B ，以便于与一端接地的激励源（s s R U ,）相连；（2）2L 为高频阻流圈，以实现零偏置的要求，121,,L C C 组成降阻式T 型匹配网络，使低值的输入电阻与较高的信号源内阻相匹配。

（3）由于集电极接地，集电极回路直流馈电应采用负电源cc V 馈电。

其中5C 为高频旁路电容，4L 为高频阻流圈。

电源负端经34,L L 馈送到发射极。

（4）0C （晶体管输出电容），A C C C L L C ,,,,,76533组成匹配网络。

,,,330L C C 并联谐振于A C C C L f ,,,,7650串联谐振于40,C f 为隔直流电容。

4-9）某晶体管高频功放,1802,30.90,2000ο===Ω=ϕV V mA I R cc c p 试求.,~ηP 【解】W V I P cc co 7.230109030=⨯⨯==- %747.222200]09.057.1[21])([2121~22121~====⨯⨯===o p co p c P P W R I g R I P ηϕ4-10）高频大功率晶体管3DA4MHZ f T 100=，饱和临界线跨导V A g cr /8.0=，用它作成2MHZ 的高频功率放大器。

选定,2.2,1402,24A I V V cm cc ===οϕ并工作于临界状态，试计算.,.,,0~ηp c R P P P【解】cc cm cc co V I r V I P ⨯==)70(cos 0οW 36.13242.2253.0=⨯⨯=因A I a I cm c 96.02.2436.0)70(11=⨯==οV g IV u V U crcmcc ce cc c 25.218.02.224min =-=-=-= 故 WU I P c c 19.1025.2196.021211~=⨯⨯==)(22)96.0(19.1022%7636.1319.1017.319.1036.131221~0~~0c cp c p c I U R I P R P P W P P P =Ω=⨯======-=-=或η4-11） 某谐振功率放大器的晶体管动态转移特性用折线表示为题图4-11所示，晶体管的极限电压.2V BV beo =（1） 基波放大时，给定,70,50ο==ϕmA I cm 求b bb U V ,为多少？（2）三倍频时，若cm I 仍为50mA 。

试求三次谐波输出最大时的b bb U V ,是多少？是否超过了.beo BV【解】（1）V A u i g be c c /2.065.09.005.0=-=∆∆=)cos (bz b bb c c V wt U V g i -+= 当cm c I i wt ==,0)65.0(2.005.0-+=b bb U V9.0=+b bb U V (1)当 ωt=ϕ t c =0 即 0=0.2(V bb +)65.0cos -ϕb Ub b bb U U V 342.065.070cos 65.00-=-= (2)联立（1） （2）解得V V bb 52.0= V U b 38.0= （2）三倍频时，（1）式仍成立，（2）式修正为：b b bb U U V 766.065.040cos 65.0-=-= （2’）联立（1） (2’)解得V V bb 17.0-= V U b 07.1=V BV V U V beo b bb 224.107.117.0||=<=+=+4－12 试画出用n 个1：1 传输线变压器和短路线组成阻抗变换为1:)1(2+n 传输线变压器的连接网络，并证明：L i R n Z )1(+=L i R n R 2)1(+= 【解】该网络如图所示： 设信号源激励电压为i U ，电流为i I ，负载电压为,L U 电流为L I由图有'21n n i U U U U U ++++=Λ由于U U U U U U n n ======'321Λ 故 U n U i )1(+=又因U U U U U n L =====''2'1Λ 故iL U n U 11+= 再因 '21n n L I I I I I ++++=Λ 由于i n n I I I I I ====='21Λ 故 i L I n I )1(+=从而 ii i i iL L L R n I U n I n U n I U R 22)1(1)1(1)1(11+=+=++==L L i c R n R R Z )1(+==4－13 试画出用n 个1：1传输线变压器和短路线组成阻抗变换为1：2)1(+n 传输线变压器的连接网络，并证明：Lc R n Z )1(1+=Li R n R 2)1(1+=【解】该网络如图所示：设信号源激励电压为i U ，电流为i I ，负载电压为L U ，电流为L I由图有n n L U U U U U ++++=''2'1'Λ 由于U U U U U n n =====''2'1Λ 故 i L U n U )1(+=再因 '21n n i I I I I I ++++=Λ由于L n n I I I I I ====='21Λ 故 L i I n I )1(+=从而 LL L L Li i i R n I U n I n U n I U R 22)1(1)1(1)1(11+=+=++==LL i c R n R R Z 11+==。